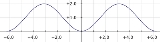
Versine
Encyclopedia
The versine or versed sine, versin(θ), is a trigonometric function
equal to and 2sin2(½θ). It appeared in some of the earliest trigonometric tables and was once widespread, but it is now little-used. There are several related functions, most notably the haversine, half the versine, known in the haversine formula
of navigation.
It is also written as vers(θ) or ver(θ). In Latin
, it is known as the sinus versus (flipped sine) or the sagitta (arrow).

s and scientific calculator
s. As θ goes to zero, versin(θ) is the difference between two nearly equal quantities, so a user of a trigonometric table for the cosine alone would need a very high accuracy to obtain the versine, making separate tables for the latter convenient. Even with a computer, round-off error
s make it advisable to use the sin2 formula for small θ. Another historical advantage of the versine is that it is always non-negative, so its logarithm
is defined everywhere except for the single angle (θ = 0, 2π,...) where it is zero—thus, one could use logarithmic tables for multiplications in formulas involving versines.
The haversine, in particular, was important in navigation
because it appears in the haversine formula
, which is used to accurately compute distances on a sphere given angular positions (e.g., longitude
and latitude
). One could also use sin2(θ/2) directly, but having a table of the haversine removed the need to compute squares and square roots. The term haversine was, apparently, coined in a navigation text for just such an application.
In fact, the earliest surviving table of sine
(half-chord
) values (as opposed to the chords tabulated by Ptolemy
and other Greek authors), from the fourth–fifth century Siddhantas from India
, was a table of values for the sine and versed sine only (in 3.75° increments from 0 to 90°). The versine appears as an intermediate step in the application of the half-angle formula sin2(θ/2) = versin(θ)/2, derived by Ptolemy
, that was used to construct such tables.
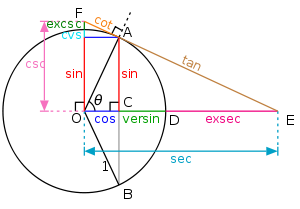
 As for sine, the etymology
As for sine, the etymology
derives from a twelfth century mistranslation of the Sanskrit
jiva via Arabic
. To contrast it with the versed sine (sinus versus), the ordinary sine function was sometimes historically called the sinus rectus ("vertical sine"). The meaning of these terms is apparent if one looks at the functions in the original context for their definition, a unit circle, shown at right. For a vertical chord AB of the unit circle, the sine of the angle θ (half the subtended angle) is the distance AC (half of the chord). On the other hand, the versed sine of θ is the distance CD from the center of the chord to the center of the arc. Thus, the sum of cos(θ) = OC and versin(θ) = CD is the radius OD = 1. Illustrated this way, the sine is vertical (rectus) while the versine is flipped on its side (versus); both are distances from C to the circle.
This figure also illustrates the reason why the versine was sometimes called the sagitta, Latin for arrow
, from the Arabic usage sahem of the same meaning. If the arc ADB is viewed as a "bow
" and the chord AB as its "string", then the versine CD is clearly the "arrow shaft".
In further keeping with the interpretation of the sine as "vertical" and the versed sine as "horizontal", sagitta is also an obsolete synonym for the abscissa
(the horizontal axis of a graph).
One period (0 < θ < π/2) of a versine or, more commonly, a haversine waveform is also commonly used in signal processing
and control theory
as the shape of a pulse
or a window function
, because it smoothly (continuous
in value and slope
) "turns on" from zero
to one (for haversine) and back to zero. In these applications, it is given yet another name: raised-cosine filter
or Hann function
.
as the chord length L goes to zero, the ratio 8v/L2 goes to the instantaneous curvature
. This usage is especially common in rail transport
, where it describes measurements of the straightness of the rail tracks
and it is the basis of the Hallade method
for rail surveying. The term sagitta (often abbreviated sag) is used similarly in optics
, for describing the surfaces of lenses
and mirror
s.
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
equal to and 2sin2(½θ). It appeared in some of the earliest trigonometric tables and was once widespread, but it is now little-used. There are several related functions, most notably the haversine, half the versine, known in the haversine formula
Haversine formula
The haversine formula is an equation important in navigation, giving great-circle distances between two points on a sphere from their longitudes and latitudes...
of navigation.
It is also written as vers(θ) or ver(θ). In Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
, it is known as the sinus versus (flipped sine) or the sagitta (arrow).
Related functions
There are several other related functions:- The versed cosine, or vercosine, written

- The coversed sine, or coversine, written
 and sometimes abbreviated to
and sometimes abbreviated to 
- The coversed cosine, or covercosine, written

- The haversed sine, or haversine, written
 , most famous from the haversine formulaHaversine formulaThe haversine formula is an equation important in navigation, giving great-circle distances between two points on a sphere from their longitudes and latitudes...
, most famous from the haversine formulaHaversine formulaThe haversine formula is an equation important in navigation, giving great-circle distances between two points on a sphere from their longitudes and latitudes...
used historically in navigationNavigationNavigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks... - The haversed cosine, or havercosine, written

- The hacoversed sine, also called hacoversine or cohaversine and written

- The hacoversed cosine, also called hacovercosine or cohavercosine and written

- The exsecant, written

- The excosecant, written


Construction of versine and related functions
For a trigonometric function fun, the above definitions correspond to the relations:
Definitions
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
Derivatives and Integrals
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
History and applications
Historically, the versed sine was considered one of the most important trigonometric functions, but it has fallen from popularity in modern times due to the availability of computerComputer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s and scientific calculator
Calculator
An electronic calculator is a small, portable, usually inexpensive electronic device used to perform the basic operations of arithmetic. Modern calculators are more portable than most computers, though most PDAs are comparable in size to handheld calculators.The first solid-state electronic...
s. As θ goes to zero, versin(θ) is the difference between two nearly equal quantities, so a user of a trigonometric table for the cosine alone would need a very high accuracy to obtain the versine, making separate tables for the latter convenient. Even with a computer, round-off error
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
s make it advisable to use the sin2 formula for small θ. Another historical advantage of the versine is that it is always non-negative, so its logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
is defined everywhere except for the single angle (θ = 0, 2π,...) where it is zero—thus, one could use logarithmic tables for multiplications in formulas involving versines.
The haversine, in particular, was important in navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
because it appears in the haversine formula
Haversine formula
The haversine formula is an equation important in navigation, giving great-circle distances between two points on a sphere from their longitudes and latitudes...
, which is used to accurately compute distances on a sphere given angular positions (e.g., longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
and latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
). One could also use sin2(θ/2) directly, but having a table of the haversine removed the need to compute squares and square roots. The term haversine was, apparently, coined in a navigation text for just such an application.
In fact, the earliest surviving table of sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
(half-chord
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
) values (as opposed to the chords tabulated by Ptolemy
Ptolemy's table of chords
The table of chords, created by the astronomer and geometer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function...
and other Greek authors), from the fourth–fifth century Siddhantas from India
India
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
, was a table of values for the sine and versed sine only (in 3.75° increments from 0 to 90°). The versine appears as an intermediate step in the application of the half-angle formula sin2(θ/2) = versin(θ)/2, derived by Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
, that was used to construct such tables.

Etymology
Etymology is the study of the history of words, their origins, and how their form and meaning have changed over time.For languages with a long written history, etymologists make use of texts in these languages and texts about the languages to gather knowledge about how words were used during...
derives from a twelfth century mistranslation of the Sanskrit
Sanskrit
Sanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
jiva via Arabic
Arabic language
Arabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
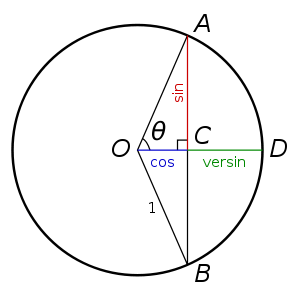
. To contrast it with the versed sine (sinus versus), the ordinary sine function was sometimes historically called the sinus rectus ("vertical sine"). The meaning of these terms is apparent if one looks at the functions in the original context for their definition, a unit circle, shown at right. For a vertical chord AB of the unit circle, the sine of the angle θ (half the subtended angle) is the distance AC (half of the chord). On the other hand, the versed sine of θ is the distance CD from the center of the chord to the center of the arc. Thus, the sum of cos(θ) = OC and versin(θ) = CD is the radius OD = 1. Illustrated this way, the sine is vertical (rectus) while the versine is flipped on its side (versus); both are distances from C to the circle.
This figure also illustrates the reason why the versine was sometimes called the sagitta, Latin for arrow
Arrow
An arrow is a shafted projectile that is shot with a bow. It predates recorded history and is common to most cultures.An arrow usually consists of a shaft with an arrowhead attached to the front end, with fletchings and a nock at the other.- History:...
, from the Arabic usage sahem of the same meaning. If the arc ADB is viewed as a "bow
Bow (weapon)
The bow and arrow is a projectile weapon system that predates recorded history and is common to most cultures.-Description:A bow is a flexible arc that shoots aerodynamic projectiles by means of elastic energy. Essentially, the bow is a form of spring powered by a string or cord...
" and the chord AB as its "string", then the versine CD is clearly the "arrow shaft".
In further keeping with the interpretation of the sine as "vertical" and the versed sine as "horizontal", sagitta is also an obsolete synonym for the abscissa
Abscissa
In mathematics, abscissa refers to that element of an ordered pair which is plotted on the horizontal axis of a two-dimensional Cartesian coordinate system, as opposed to the ordinate...
(the horizontal axis of a graph).
One period (0 < θ < π/2) of a versine or, more commonly, a haversine waveform is also commonly used in signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
and control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
as the shape of a pulse
Pulse (signal processing)
In signal processing, the term pulse has the following meanings:#A rapid, transient change in the amplitude of a signal from a baseline value to a higher or lower value, followed by a rapid return to the baseline value....
or a window function
Window function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
, because it smoothly (continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
in value and slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
) "turns on" from zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
to one (for haversine) and back to zero. In these applications, it is given yet another name: raised-cosine filter
Raised-cosine filter
The raised-cosine filter is a filter frequently used for pulse-shaping in digital modulation due to its ability to minimise intersymbol interference...
or Hann function
Hann function
The Hann function, named after the Austrian meteorologist Julius von Hann, is a discrete probability mass function given byw= 0.5\; \leftorw= \sin^2 \left...
.
"Versines" of arbitrary curves and chords
The term versine is also sometimes used to describe deviations from straightness in an arbitrary planar curve, of which the above circle is a special case. Given a chord between two points in a curve, the perpendicular distance v from the chord to the curve (usually at the chord midpoint) is called a versine measurement. For a straight line, the versine of any chord is zero, so this measurement characterizes the straightness of the curve. In the limitLimit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
as the chord length L goes to zero, the ratio 8v/L2 goes to the instantaneous curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
. This usage is especially common in rail transport
Rail transport
Rail transport is a means of conveyance of passengers and goods by way of wheeled vehicles running on rail tracks. In contrast to road transport, where vehicles merely run on a prepared surface, rail vehicles are also directionally guided by the tracks they run on...
, where it describes measurements of the straightness of the rail tracks
Rail tracks
The track on a railway or railroad, also known as the permanent way, is the structure consisting of the rails, fasteners, sleepers and ballast , plus the underlying subgrade...
and it is the basis of the Hallade method
Hallade method
The Hallade method, devised by Frenchman Emile Hallade, is a method of surveying, designing and setting out curves in railway track.It involves measuring the offset of a string line from the outside of a curve at the central point of a chord. A standard chord length is used: in the UK this is...
for rail surveying. The term sagitta (often abbreviated sag) is used similarly in optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, for describing the surfaces of lenses
Lens (optics)
A lens is an optical device with perfect or approximate axial symmetry which transmits and refracts light, converging or diverging the beam. A simple lens consists of a single optical element...
and mirror
Mirror
A mirror is an object that reflects light or sound in a way that preserves much of its original quality prior to its contact with the mirror. Some mirrors also filter out some wavelengths, while preserving other wavelengths in the reflection...
s.
See also
- Trigonometric identities
- Exsecant
External links
- Sagitta, Apothem, and Chord by Ed Pegg, Jr.Ed Pegg, Jr.Ed Pegg, Jr. is an expert on mathematical puzzles and is a self-described recreational mathematician. He creates puzzles for the Mathematical Association of America online at Ed Pegg, Jr.'s Math Games. His puzzles have also been used by Will Shortz on the puzzle segment of NPR's Weekend Edition...
, The Wolfram Demonstrations Project.

