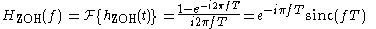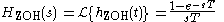
Zero-order hold
Encyclopedia
The zero-order hold is a mathematical model of the practical signal reconstruction
done by a conventional digital-to-analog converter
(DAC). That is, it describes the effect of converting a discrete-time signal to a continuous-time signal by holding each sample value for one sample interval. It has several applications in electrical communication.
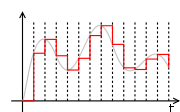
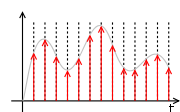A zero-order hold reconstructs the following continuous-time waveform from a sample sequence x[n], assuming one sample per time interval T:
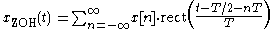
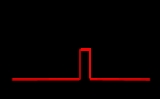
The function
is depicted in Figure 1, and 
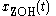is the piecewise-constant signal depicted in Figure 2.
with impulse response equal to a rect function, and with input being a sequence of dirac impulses
scaled to the sample values. The filter can then be analyzed in the frequency domain, for comparison with other reconstruction methods such as the Whittaker–Shannon interpolation formula
suggested by the Nyquist–Shannon sampling theorem
, or such as the first-order hold
or linear interpolation between sample values.
In this method, a sequence of dirac impulses
, xs(t), representing the discrete samples, x[n], is low-pass filter
ed to recover a continuous-time signal, x(t).
Even though this is not what a DAC does in reality, the DAC output can be modeled by applying the hypothetical sequence of dirac impulses, xs(t), to a linear, time-invariant filter with such characteristics (which, for an LTI system, are fully described by the impulse response
) so that each input impulse results in the correct constant pulse in the output.
Begin by defining a continuous-time signal from the sample values, as above but using delta functions instead of rect functions:
Signal reconstruction
In signal processing, reconstruction usually means the determination of an original continuous signal from a sequence of equally spaced samples.This article takes a generalized abstract mathematical approach to signal sampling and reconstruction...
done by a conventional digital-to-analog converter
Digital-to-analog converter
In electronics, a digital-to-analog converter is a device that converts a digital code to an analog signal . An analog-to-digital converter performs the reverse operation...
(DAC). That is, it describes the effect of converting a discrete-time signal to a continuous-time signal by holding each sample value for one sample interval. It has several applications in electrical communication.
Time-domain model
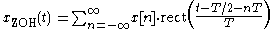
- where
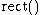is the rectangular function.
The function
is depicted in Figure 1, and 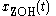is the piecewise-constant signal depicted in Figure 2.Frequency-domain model
The equation above for the output of the ZOH can also be modeled as the output of a linear time-invariant filterLTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
with impulse response equal to a rect function, and with input being a sequence of dirac impulses
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
scaled to the sample values. The filter can then be analyzed in the frequency domain, for comparison with other reconstruction methods such as the Whittaker–Shannon interpolation formula
Whittaker–Shannon interpolation formula
The Whittaker–Shannon interpolation formula or sinc interpolation is a method to reconstruct a continuous-time bandlimited signal from a set of equally spaced samples.-Definition:...
suggested by the Nyquist–Shannon sampling theorem
Nyquist–Shannon sampling theorem
The Nyquist–Shannon sampling theorem, after Harry Nyquist and Claude Shannon, is a fundamental result in the field of information theory, in particular telecommunications and signal processing. Sampling is the process of converting a signal into a numeric sequence...
, or such as the first-order hold
First-order hold
The first-order hold is a mathematical model of the practical reconstruction of sampled signals that could be done by a conventional digital-to-analog converter and an analog circuit called an integrator. For the FOH, the signal is reconstructed as a piecewise linear approximation to the...
or linear interpolation between sample values.
In this method, a sequence of dirac impulses
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
, xs(t), representing the discrete samples, x[n], is low-pass filter
Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
ed to recover a continuous-time signal, x(t).
Even though this is not what a DAC does in reality, the DAC output can be modeled by applying the hypothetical sequence of dirac impulses, xs(t), to a linear, time-invariant filter with such characteristics (which, for an LTI system, are fully described by the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
) so that each input impulse results in the correct constant pulse in the output.
Begin by defining a continuous-time signal from the sample values, as above but using delta functions instead of rect functions:
-
The scaling by T, which arises naturally by time-scaling the delta function, has the result that the mean value of xs(t) is equal to the mean value of the samples, so that the lowpass filter needed will have a DC gain of 1. Some authors use this scaling, while many others omit the time-scaling and the T, resulting in a low-pass filter model with a DC gain of T, and hence dependent on the units of measurement of time.
The zero-order hold is the hypothetical filterFilter (signal processing)In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal...
or LTI system that converts the sequence of modulated Dirac impulses xs(t)to the piecewise-constant signal (shown in Figure 2):
resulting in an effective impulse responseImpulse responseIn signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
(shown in Figure 4) of:
-
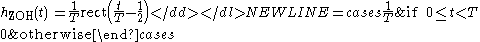
The effective frequency response is the continuous Fourier transformContinuous Fourier transformThe Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...
of the impulse response.
- where
is the (normalized) sinc function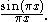 
used in digital signal processing.
The Laplace transform transfer functionTransfer functionA transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
of the ZOH is found by substituting s = i 2 π f:
The fact that practical digital-to-analog converterDigital-to-analog converterIn electronics, a digital-to-analog converter is a device that converts a digital code to an analog signal . An analog-to-digital converter performs the reverse operation...
s (DAC) do not output a sequence of dirac impulses, xs(t) (that, if ideally low-pass filtered, would result in the unique underlying bandlimited signal before sampling), but instead output a sequence of rectangular pulses, xZOH(t) (a piecewise constant function), means that there is an inherent effect of the ZOH on the effective frequency response of the DAC, resulting in a mild roll-offRoll-offRoll-off is a term commonly used to describe the steepness of a transmission function with frequency, particularly in electrical network analysis, and most especially in connection with filter circuits in the transition between a passband and a stopband...
of gain at the higher frequencies (a 3.9224 dB loss at the Nyquist frequencyNyquist frequencyThe Nyquist frequency, named after the Swedish-American engineer Harry Nyquist or the Nyquist–Shannon sampling theorem, is half the sampling frequency of a discrete signal processing system...
, corresponding to a gain of sinc(1/2) = 2/π). This droop is a consequence of the hold property of a conventional DAC, and is not due to the sample and holdSample and holdIn electronics, a sample and hold circuit is an analog device that samples the voltage of a continuously varying analog signal and holds its value at a constant level for a specified minimal period of time. Sample and hold circuits and related peak detectors are the elementary analog memory...
that might precede a conventional analog-to-digital converterAnalog-to-digital converterAn analog-to-digital converter is a device that converts a continuous quantity to a discrete time digital representation. An ADC may also provide an isolated measurement...
(ADC). -
-
