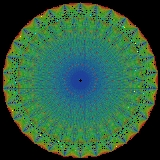
An Exceptionally Simple Theory of Everything
Encyclopedia
"An Exceptionally Simple Theory of Everything" is a preprint
proposing a basis for a unified field theory
, very often referred to as "E8 Theory," which attempts to describe all known fundamental interaction
s in physics
and to stand as a possible theory of everything
. The paper was posted to the physics arXiv
by Antony Garrett Lisi
on November 6, 2007, and was not submitted to a peer-reviewed scientific journal
. The title is a pun
on the algebra used, the Lie algebra
of the largest "simple
," "exceptional" Lie group
, E8
. Using representation theory
, the paper describes how the combined structure of all gravitational and Standard Model
forces acting on a generation of fermions is part of the E8 Lie algebra. In the paper, Lisi states that all three generations of fermions do not directly embed in E8 with correct quantum numbers, but might be described via a triality
transformation, noting that the theory is incomplete.
The theory received accolades from a few physicists amid a flurry of media coverage, but also met with widespread skepticism. Scientific American
reported in March 2008 that the theory was being "largely but not entirely ignored" by the mainstream physics community, with a few physicists picking up the work to develop it further.
As of May 2008 Lisi's preprint was the most downloaded article in the arXiv.
In July 2009 Jacques Distler
and Skip Garibaldi
published a critical paper in Communications in Mathematical Physics
called "There is no 'Theory of Everything' inside E8," arguing that Lisi's theory, and a large class of related models, cannot work. They offer a direct proof that it is impossible to embed all three generations of fermions in E8, or to obtain even the one-generation Standard Model without the presence of an antigeneration. In response to Distler and Garibaldi's paper, Lisi argues that some assumptions about fermion embeddings are unnecessary and that the antigeneration is not per se a problem sufficient to rule out the one-generation Standard Model.
In June 2010 Lisi posted a new paper on E8 Theory, "An Explicit Embedding of Gravity and the Standard Model in E8," peer reviewed and accepted for publication in a conference proceedings, describing the explicit embedding of one generation using matrix representations. In September 2010 Scientific American reported on a conference inspired by Lisi's work. In October 2010, Lisi, Lee Smolin
and Simone Speziale published a partially related paper on unification, in a peer-reviewed journal, proposing an action and symmetry breaking mechanism, and using an alternative treatment of fermions. In December 2010 Scientific American published a feature article on E8 Theory, "A Geometric Theory of Everything," written by Lisi and James Owen Weatherall. In May 2011 Lisi wrote a follow-up letter describing criticism of E8 Theory and how it has progressed, noting that the theory is still incomplete and makes only tenuous predictions, with the three generation issue remaining as a significant problem.
(a "GUT," describing electromagnetism
, the weak interaction
and the strong interaction
) to include gravitation
, a Higgs boson
and fermions in an attempt to describe all fields of the Standard Model
and gravity as different parts of one field
over four dimensional spacetime. More specifically, Lisi combines the left-right symmetric
Pati-Salam GUT
with a MacDowell-Mansouri
description of gravity, using the spin connection
and gravitational frame
combined with a Higgs boson, necessitating a cosmological constant
. The model is formulated as a gauge theory
, using a modified BF action
, with E8
as the Lie group
. Mathematically, this is an E8 principal bundle
, with connection
, over a four dimensional base manifold
. Lisi's embedding of the Standard Model gauge group in E8 leads him to predict the existence of 22 new boson
ic particles at an undetermined mass scale.
The fermions enter, via an unconventional use of the BRST technique
, as Grassmann number
fields valued in part of the E8 Lie algebra. The bosons are combined with these fermions as one-form
and Grassmann number parts of a kind of superconnection, each valued in separate parts of the E8 Lie algebra. The curvature
of this superconnection is calculated, producing the Riemann curvature
, gauge field curvature
, gravitational torsion
, covariant derivative
of the Higgs, and the covariant Dirac derivative
of the fermions. This curvature is used to build the modified BF action by hand, in an attempt to match the dynamics of the Standard Model and gravity.
In the paper, Lisi describes several deficiencies in this model. The most important deficiency is noted as an incorrect, or "poorly understood," inclusion of the second and third generations
of fermions in E8, relying on triality
. This deficiency, and the incomplete nature of the model, precludes the prediction of masses for new or existing particles. Also, Lisi notes the use of explicit symmetry breaking
in building his action, rather than offering a more desirable spontaneous symmetry breaking
mechanism. And, no attempt is made to provide a quantum description
of the theory—this being left for future work.
In a follow-up paper, Lee Smolin
proposes a spontaneous symmetry breaking mechanism for obtaining the action in Lisi's model, and speculates on the path to its quantization as a spin foam
.
, with many different sphere
s glued to the surface—one sphere at each surface point, and each sphere attached by one point. This geometric construction is a fiber bundle
, with the spheres as the "fibers," and the wavy surface as the "base". A sphere can be rotated in three different ways: around the x-axis, the y-axis, or around the z-axis. Each of these rotations corresponds to a symmetry
of the sphere. The fiber bundle connection
is a field
describing how spheres at nearby surface points are related, in terms of these three different rotations. The geometry of the fiber bundle is described by the curvature
of this connection. In the corresponding quantum field theory
, there is a particle associated with each of these three symmetries, and these particles can interact according to the geometry of a sphere.
In Lisi's model, the base is a four-dimensional surface—our spacetime
—and the fiber is the E8
Lie group
, a complicated 248-dimensional shape, which some mathematicians consider to be the most beautiful shape in mathematics. In each gauge theory based on a Yang-Mills action, the symmetries of the Lie group are associated to particles, called gauge bosons (like photons, W and Z bosons, and gluons in the Standard Model), which can interact with each other and with fermions according to the geometry of the group and its fundamental representations. In general, a unified theory has a Lie group large enough to contain the Standard Model symmetries. There are many such theories, some of which also use E8. In Lisi's specific model, each of the 248 symmetries of E8 corresponds to a different elementary particle
(including gravitons and fermions), which can interact, as usual, according to the geometry of the group, in this case E8. As Lisi describes it: "The principal bundle connection and its curvature describe how the E8 manifold twists and turns over spacetime, reproducing all known fields and dynamics through pure geometry."
The complicated geometry of Lie groups, E8 amongst them, is described graphically using group representation
theory. Using this mathematical description, each symmetry of a group—and so each kind of elementary particle—can be associated with a point in a diagram. The coordinates of these points are the quantum numbers—the charges
—of elementary particles, which are conserved in interactions. Such a diagram sits in a flat, Euclidean space
of some dimension, forming a polytope
, such as the 421 polytope
in eight-dimensional space.
In order to form a theory of everything
, Lisi's model must eventually predict the exact number of fundamental particles
, all of their properties, mass
es, forces between them
, the nature of spacetime
, and the cosmological constant
. Much of this work is still in the conceptual stage—in particular, quantization
and predictions of particle masses
have not been done. And Lisi himself acknowledges it as a work-in-progress: "The theory is very young, and still in development."
. "Clifford bundle formulation of BF gravity generalized to the standard model," in 2005, describes the algebra of gravitational and Standard Model fields acting on a generation of fermions, but does not mention E8. "Quantum mechanics from a universal action reservoir," in 2006, attempts to derive quantum mechanics using information theory.
Before writing his 2007 paper, Lisi discussed his work on an FQXi forum, at an FQXi conference, and for an FQXi article. Lisi gave his first talk on E8 Theory at the Loops '07 conference in Morelia
, Mexico
, soon followed by a talk at the Perimeter Institute. John Baez commented on Lisi's work in "This Week's Finds in Mathematical Physics (Week 253)," and Lisi was interviewed on Sabine Hossenfelder's "Backreaction" blog. Lisi's arXiv preprint, "An Exceptionally Simple Theory of Everything," appeared on November 6, 2007, and immediately attracted a great deal of attention. Lisi made a further presentation for the International Loop Quantum Gravity Seminar on November 13, 2007, and responded to press inquiries on an FQXi forum. He presented his work at the TED Conference
on February 28, 2008.
Numerous news sites from all over the world reported on the new theory in 2007 and 2008, noting Lisi's personal history and the controversy in the physics community. The first mainstream and scientific press coverage began with articles in The Daily Telegraph
and New Scientist
, with articles soon following in Wired News
, Le Monde
, The Economist
, The Daily Telegraph
, Discover Magazine, Wired Magazine, Scientific American
, Physics World
, Symmetry Magazine and The New Yorker
.
Lisi's paper spawned a variety of reactions and debates across various physics blog
s and online discussion groups. The first to comment was Sabine Hossenfelder, summarizing the paper and noting the lack of a dynamical symmetry breaking mechanism.
Luboš Motl
offered a colorful critique, objecting to the addition of bosons and fermions in Lisi's superconnection, and to the violation of the Coleman-Mandula theorem
. Further discussions, often including Lisi, took place on Peter Woit's
Not Even Wrong, Sean Carroll's
Cosmic Variance, Steinn Sigurðsson's Dynamics of Cats, Physics Forums, Slashdot
, Digg
, and Reddit
. In the presentation "What's new at the arXiv?" on May 20, 2008, Simeon Warner stated that Lisi's paper is the most downloaded article on the arXiv. Among the physicists early to comment on E8 Theory, Sabine Hossenfelder, Peter Woit and Lee Smolin
were generally supportive, while Luboš Motl and Jacques Distler
were critical.
On his blog, Musings, Jacques Distler offered one of the strongest criticisms of Lisi's approach, claiming to demonstrate that, unlike in the Standard Model, Lisi's model is nonchiral — consisting of a generation and an anti-generation — and to prove that any alternative embedding in E8 must be similarly nonchiral. These arguments were distilled in a paper written jointly with Skip Garibaldi, "There is no 'Theory of Everything' inside E8," published in Communications in Mathematical Physics
. In this paper, Distler and Garibaldi offer a proof that it is impossible to embed all three generations of fermions in E8, or to obtain even the one-generation Standard Model. In a press release from his university, "Rock climber takes on surfer's theory," Garibaldi states that his article with Distler is a rebuttal of Lisi's theory. In response, Lisi argues that Distler and Garibaldi made unnecessary assumptions about how the embedding needs to happen. Addressing the one generation case, Lisi posted a new paper, "An Explicit Embedding of Gravity and the Standard Model in E8," describing how the algebra of gravity and the Standard Model with one generation of fermions embeds in the E8 Lie algebra explicitly using matrix representations. When this embedding is done, Lisi agrees that there is an antigeneration of fermions (also known as "mirror fermions") remaining in E8; but while Distler and Garibaldi state that these mirror fermions make the theory nonchiral, Lisi states that these mirror fermions might have high masses, making the theory chiral, or that they might be related to the other generations. Addressing the three generation case, Lisi agrees that three generations of fermions cannot be directly embedded in E8, but suggests that a gauge transformation related to triality
might be used to relate the 64 mirror fermions and 64 other E8 generators to two other generations of 64 fermions.
The group blog, The n-Category Cafe, provides some of the more technical discussions, with posts by Lisi, Urs Schreiber, Kea, and Jacques Distler.
Sixteen arXiv preprints have cited Lisi's work. Lee Smolin
's "The Plebanski action extended to a unification of gravity and Yang-Mills theory," December 6, 2007, proposes a symmetry breaking mechanism to go from an E8 symmetric action to Lisi's action for the Standard Model and gravity. Roberto Percacci's "Mixing internal and spacetime transformations: some examples and counterexamples" addresses a general loophole in the Coleman-Mandula theorem also thought to work in E8 Theory. Percacci and Fabrizio Nesti's "Chirality in unified theories of gravity" confirms the embedding of the algebra of gravitational and Standard Model forces acting on a generation of fermions in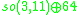
, mentioning that Lisi's "ambitious attempt to unify all known fields into a single representation of E8 stumbled into chirality issues." Mathematician Bertram Kostant
discussed Lisi's work in a colloquium presentation at UC Riverside. In a joint paper with Lee Smolin and Simone Speziale, published in Journal of Physics A
, Lisi proposes a new action and symmetry breaking mechanism. In "An Explicit Embedding of Gravity and the Standard Model in E8," Lisi describes E8 Theory using explicit matrix representations.
On August 4, 2008, FQXi awarded Lisi a grant for further development of E8 Theory.
In September 2010 the popular magazine Scientific American reported on a conference in Banff inspired by Lisi's work. In December 2010 Scientific American published a feature article on E8 Theory, "A Geometric Theory of Everything." In May 2011 Lisi wrote a follow-up letter for Scientific American, describing criticism of E8 Theory and how it has progressed, noting that the theory is still incomplete, with the three generation issue remaining as a significant problem.
Preprint
A preprint is a draft of a scientific paper that has not yet been published in a peer-reviewed scientific journal.-Role:Publication of manuscripts in a peer-reviewed journal often takes weeks, months or even years from the time of initial submission, because manuscripts must undergo extensive...
proposing a basis for a unified field theory
Unified field theory
In physics, a unified field theory, occasionally referred to as a uniform field theory, is a type of field theory that allows all that is usually thought of as fundamental forces and elementary particles to be written in terms of a single field. There is no accepted unified field theory, and thus...
, very often referred to as "E8 Theory," which attempts to describe all known fundamental interaction
Fundamental interaction
In particle physics, fundamental interactions are the ways that elementary particles interact with one another...
s in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and to stand as a possible theory of everything
Theory of everything
A theory of everything is a putative theory of theoretical physics that fully explains and links together all known physical phenomena, and predicts the outcome of any experiment that could be carried out in principle....
. The paper was posted to the physics arXiv
ArXiv
The arXiv |Chi]], χ) is an archive for electronic preprints of scientific papers in the fields of mathematics, physics, astronomy, computer science, quantitative biology, statistics, and quantitative finance which can be accessed online. In many fields of mathematics and physics, almost all...
by Antony Garrett Lisi
Antony Garrett Lisi
Antony Garrett Lisi , who uses the name Garrett by preference, is an American theoretical physicist and adventure sports enthusiast. Lisi works as an independent researcher without an academic position...
on November 6, 2007, and was not submitted to a peer-reviewed scientific journal
Scientific journal
In academic publishing, a scientific journal is a periodical publication intended to further the progress of science, usually by reporting new research. There are thousands of scientific journals in publication, and many more have been published at various points in the past...
. The title is a pun
Pun
The pun, also called paronomasia, is a form of word play which suggests two or more meanings, by exploiting multiple meanings of words, or of similar-sounding words, for an intended humorous or rhetorical effect. These ambiguities can arise from the intentional use and abuse of homophonic,...
on the algebra used, the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of the largest "simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
," "exceptional" Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, E8
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
. Using representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, the paper describes how the combined structure of all gravitational and Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
forces acting on a generation of fermions is part of the E8 Lie algebra. In the paper, Lisi states that all three generations of fermions do not directly embed in E8 with correct quantum numbers, but might be described via a triality
Triality
In mathematics, triality is a relationship between three vector spaces, analogous to the duality relation between dual vector spaces. Most commonly, it describes those special features of the Dynkin diagram D4 and the associated Lie group Spin, the double cover of 8-dimensional rotation group SO,...
transformation, noting that the theory is incomplete.
The theory received accolades from a few physicists amid a flurry of media coverage, but also met with widespread skepticism. Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
reported in March 2008 that the theory was being "largely but not entirely ignored" by the mainstream physics community, with a few physicists picking up the work to develop it further.
As of May 2008 Lisi's preprint was the most downloaded article in the arXiv.
In July 2009 Jacques Distler
Jacques Distler
Jacques Distler is a physicist currently working in string theory. He has been a professor of physics at the University of Texas at Austin since 1994.-Early life and education:...
and Skip Garibaldi
Skip Garibaldi
Skip Garibaldi is an American mathematician doing research on algebraic groups and especially exceptional groups. He is currently Winship Distinguished Research Professor at Emory University.-Biography:...
published a critical paper in Communications in Mathematical Physics
Communications in Mathematical Physics
Communications in Mathematical Physics is a peer-reviewed academic journal published by Springer. The journal publishes papers in all fields of mathematical physics, but focuses particularly in Analysis related to condensed matter physics, statistical mechanics and quantum field theory, and in...
called "There is no 'Theory of Everything' inside E8," arguing that Lisi's theory, and a large class of related models, cannot work. They offer a direct proof that it is impossible to embed all three generations of fermions in E8, or to obtain even the one-generation Standard Model without the presence of an antigeneration. In response to Distler and Garibaldi's paper, Lisi argues that some assumptions about fermion embeddings are unnecessary and that the antigeneration is not per se a problem sufficient to rule out the one-generation Standard Model.
In June 2010 Lisi posted a new paper on E8 Theory, "An Explicit Embedding of Gravity and the Standard Model in E8," peer reviewed and accepted for publication in a conference proceedings, describing the explicit embedding of one generation using matrix representations. In September 2010 Scientific American reported on a conference inspired by Lisi's work. In October 2010, Lisi, Lee Smolin
Lee Smolin
Lee Smolin is an American theoretical physicist, a researcher at the Perimeter Institute for Theoretical Physics, and an adjunct professor of physics at the University of Waterloo. He is married to Dina Graser, a communications lawyer in Toronto. His brother is David M...
and Simone Speziale published a partially related paper on unification, in a peer-reviewed journal, proposing an action and symmetry breaking mechanism, and using an alternative treatment of fermions. In December 2010 Scientific American published a feature article on E8 Theory, "A Geometric Theory of Everything," written by Lisi and James Owen Weatherall. In May 2011 Lisi wrote a follow-up letter describing criticism of E8 Theory and how it has progressed, noting that the theory is still incomplete and makes only tenuous predictions, with the three generation issue remaining as a significant problem.
Overview
Lisi's model is a variant and extension of a Grand Unification TheoryGrand unification theory
The term Grand Unified Theory, often abbreviated as GUT, refers to any of several similar candidate models in particle physics in which at high-energy, the three gauge interactions of the Standard Model which define the electromagnetic, weak, and strong interactions, are merged into one single...
(a "GUT," describing electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, the weak interaction
Weak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
and the strong interaction
Strong interaction
In particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
) to include gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
, a Higgs boson
Higgs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
and fermions in an attempt to describe all fields of the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
and gravity as different parts of one field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
over four dimensional spacetime. More specifically, Lisi combines the left-right symmetric
Left-right symmetry
Left–right symmetry is a general principle in physics which holds that valid physical laws must not produce a different result for a motion that is left-handed than motion that is right-handed...
Pati-Salam GUT
Pati-Salam model
In physics, the Pati–Salam model is a Grand Unification Theory was proposed in 1974 by nobel laureate Abdus Salam and Jogesh Pati. The unification is based on there being four quark color charges, dubbed red, green, blue and violet , instead of the conventional three, with the new "violet" quark...
with a MacDowell-Mansouri
MacDowell-Mansouri action
The MacDowell–Mansouri action is a mathematical object that is used to derive Einstein's field equations of general relativity....
description of gravity, using the spin connection
Spin connection
In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the Levi-Civita connection...
and gravitational frame
Frame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
combined with a Higgs boson, necessitating a cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
. The model is formulated as a gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, using a modified BF action
BF model
The BF model is a topological field theory, which when quantized, becomes a topological quantum field theory. BF stands for background field...
, with E8
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
as the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
. Mathematically, this is an E8 principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
, with connection
Connection (principal bundle)
In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...
, over a four dimensional base manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. Lisi's embedding of the Standard Model gauge group in E8 leads him to predict the existence of 22 new boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
ic particles at an undetermined mass scale.
The fermions enter, via an unconventional use of the BRST technique
BRST quantization
In theoretical physics, BRST quantization is a relatively rigorous mathematical approach to quantizing a field theory with a gauge symmetry...
, as Grassmann number
Grassmann number
In mathematical physics, a Grassmann number, named after Hermann Grassmann, is a mathematical construction which allows a path integral representation for Fermionic fields...
fields valued in part of the E8 Lie algebra. The bosons are combined with these fermions as one-form
One-form
In linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...
and Grassmann number parts of a kind of superconnection, each valued in separate parts of the E8 Lie algebra. The curvature
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
of this superconnection is calculated, producing the Riemann curvature
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
, gauge field curvature
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
, gravitational torsion
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
, covariant derivative
Gauge covariant derivative
The gauge covariant derivative is like a generalization of the covariant derivative used in general relativity. If a theory has gauge transformations, it means that some physical properties of certain equations are preserved under those transformations...
of the Higgs, and the covariant Dirac derivative
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
of the fermions. This curvature is used to build the modified BF action by hand, in an attempt to match the dynamics of the Standard Model and gravity.
In the paper, Lisi describes several deficiencies in this model. The most important deficiency is noted as an incorrect, or "poorly understood," inclusion of the second and third generations
Generation (particle physics)
In particle physics, a generation is a division of the elementary particles. Between generations, particles differ by their quantum number and mass, but their interactions are identical....
of fermions in E8, relying on triality
Triality
In mathematics, triality is a relationship between three vector spaces, analogous to the duality relation between dual vector spaces. Most commonly, it describes those special features of the Dynkin diagram D4 and the associated Lie group Spin, the double cover of 8-dimensional rotation group SO,...
. This deficiency, and the incomplete nature of the model, precludes the prediction of masses for new or existing particles. Also, Lisi notes the use of explicit symmetry breaking
Explicit symmetry breaking
Explicit symmetry breaking indicates a situation where the dynamical equations are not manifestly invariant under the symmetry group considered. This means, in the Lagrangian formulation, that the Lagrangian of the system contains one or more terms explicitly breaking the symmetry...
in building his action, rather than offering a more desirable spontaneous symmetry breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
mechanism. And, no attempt is made to provide a quantum description
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
of the theory—this being left for future work.
In a follow-up paper, Lee Smolin
Lee Smolin
Lee Smolin is an American theoretical physicist, a researcher at the Perimeter Institute for Theoretical Physics, and an adjunct professor of physics at the University of Waterloo. He is married to Dina Graser, a communications lawyer in Toronto. His brother is David M...
proposes a spontaneous symmetry breaking mechanism for obtaining the action in Lisi's model, and speculates on the path to its quantization as a spin foam
Spin foam
In physics, a spin foam is a topological structure made out of two-dimensional faces that represents one of the configurations that must be summed to obtain a Feynman's path integral description of quantum gravity...
.
Non-technical overview
Consider a wavy, two-dimensional surfaceSurface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, with many different sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s glued to the surface—one sphere at each surface point, and each sphere attached by one point. This geometric construction is a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
, with the spheres as the "fibers," and the wavy surface as the "base". A sphere can be rotated in three different ways: around the x-axis, the y-axis, or around the z-axis. Each of these rotations corresponds to a symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of the sphere. The fiber bundle connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
is a field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
describing how spheres at nearby surface points are related, in terms of these three different rotations. The geometry of the fiber bundle is described by the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of this connection. In the corresponding quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, there is a particle associated with each of these three symmetries, and these particles can interact according to the geometry of a sphere.
In Lisi's model, the base is a four-dimensional surface—our spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
—and the fiber is the E8
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, a complicated 248-dimensional shape, which some mathematicians consider to be the most beautiful shape in mathematics. In each gauge theory based on a Yang-Mills action, the symmetries of the Lie group are associated to particles, called gauge bosons (like photons, W and Z bosons, and gluons in the Standard Model), which can interact with each other and with fermions according to the geometry of the group and its fundamental representations. In general, a unified theory has a Lie group large enough to contain the Standard Model symmetries. There are many such theories, some of which also use E8. In Lisi's specific model, each of the 248 symmetries of E8 corresponds to a different elementary particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
(including gravitons and fermions), which can interact, as usual, according to the geometry of the group, in this case E8. As Lisi describes it: "The principal bundle connection and its curvature describe how the E8 manifold twists and turns over spacetime, reproducing all known fields and dynamics through pure geometry."
The complicated geometry of Lie groups, E8 amongst them, is described graphically using group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
theory. Using this mathematical description, each symmetry of a group—and so each kind of elementary particle—can be associated with a point in a diagram. The coordinates of these points are the quantum numbers—the charges
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
—of elementary particles, which are conserved in interactions. Such a diagram sits in a flat, Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of some dimension, forming a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
, such as the 421 polytope
Gosset 4 21 polytope
In 8-dimensional geometry, the 421 is a semiregular uniform 8-polytope, constructed within the symmetry of the E8 group. It was discovered by Thorold Gosset, published in his 1900 paper...
in eight-dimensional space.
In order to form a theory of everything
Theory of everything
A theory of everything is a putative theory of theoretical physics that fully explains and links together all known physical phenomena, and predicts the outcome of any experiment that could be carried out in principle....
, Lisi's model must eventually predict the exact number of fundamental particles
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
, all of their properties, mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
es, forces between them
Fundamental interaction
In particle physics, fundamental interactions are the ways that elementary particles interact with one another...
, the nature of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, and the cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
. Much of this work is still in the conceptual stage—in particular, quantization
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
and predictions of particle masses
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
have not been done. And Lisi himself acknowledges it as a work-in-progress: "The theory is very young, and still in development."
Chronology and reaction
Three previous arXiv preprints by Lisi deal with mathematical physics related to the theory. "Clifford Geometrodynamics," in 2002, endeavors to describe fermions geometrically as BRST ghostsBRST quantization
In theoretical physics, BRST quantization is a relatively rigorous mathematical approach to quantizing a field theory with a gauge symmetry...
. "Clifford bundle formulation of BF gravity generalized to the standard model," in 2005, describes the algebra of gravitational and Standard Model fields acting on a generation of fermions, but does not mention E8. "Quantum mechanics from a universal action reservoir," in 2006, attempts to derive quantum mechanics using information theory.
Before writing his 2007 paper, Lisi discussed his work on an FQXi forum, at an FQXi conference, and for an FQXi article. Lisi gave his first talk on E8 Theory at the Loops '07 conference in Morelia
Morelia
Morelia is a city and municipality in the north central part of the state of Michoacán in central Mexico. The city is in the Guayangareo Valley and is the capital of the state. The main pre-Hispanic cultures here were the P'urhépecha and the Matlatzinca, but no major cities were founded in the...
, Mexico
Mexico
The United Mexican States , commonly known as Mexico , is a federal constitutional republic in North America. It is bordered on the north by the United States; on the south and west by the Pacific Ocean; on the southeast by Guatemala, Belize, and the Caribbean Sea; and on the east by the Gulf of...
, soon followed by a talk at the Perimeter Institute. John Baez commented on Lisi's work in "This Week's Finds in Mathematical Physics (Week 253)," and Lisi was interviewed on Sabine Hossenfelder's "Backreaction" blog. Lisi's arXiv preprint, "An Exceptionally Simple Theory of Everything," appeared on November 6, 2007, and immediately attracted a great deal of attention. Lisi made a further presentation for the International Loop Quantum Gravity Seminar on November 13, 2007, and responded to press inquiries on an FQXi forum. He presented his work at the TED Conference
TED (conference)
TED is a global set of conferences owned by the private non-profit Sapling Foundation, formed to disseminate "ideas worth spreading"....
on February 28, 2008.
Numerous news sites from all over the world reported on the new theory in 2007 and 2008, noting Lisi's personal history and the controversy in the physics community. The first mainstream and scientific press coverage began with articles in The Daily Telegraph
The Daily Telegraph
The Daily Telegraph is a daily morning broadsheet newspaper distributed throughout the United Kingdom and internationally. The newspaper was founded by Arthur B...
and New Scientist
New Scientist
New Scientist is a weekly non-peer-reviewed English-language international science magazine, which since 1996 has also run a website, covering recent developments in science and technology for a general audience. Founded in 1956, it is published by Reed Business Information Ltd, a subsidiary of...
, with articles soon following in Wired News
Wired News
Wired News is an online technology news website, formerly known as HotWired, that split off from Wired magazine when the magazine was purchased by Condé Nast Publishing in the 1990s. Wired News was owned by Lycos not long after the split, until Condé Nast purchased Wired News on July 11, 2006...
, Le Monde
Le Monde
Le Monde is a French daily evening newspaper owned by La Vie-Le Monde Group and edited in Paris. It is one of two French newspapers of record, and has generally been well respected since its first edition under founder Hubert Beuve-Méry on 19 December 1944...
, The Economist
The Economist
The Economist is an English-language weekly news and international affairs publication owned by The Economist Newspaper Ltd. and edited in offices in the City of Westminster, London, England. Continuous publication began under founder James Wilson in September 1843...
, The Daily Telegraph
The Daily Telegraph
The Daily Telegraph is a daily morning broadsheet newspaper distributed throughout the United Kingdom and internationally. The newspaper was founded by Arthur B...
, Discover Magazine, Wired Magazine, Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
, Physics World
Physics World
Physics World is the membership magazine of the Institute of Physics, one of the largest physical societies in the world. It is an international monthly magazine covering all areas of physics, both pure and applied, and is aimed at physicists in research, industry and education worldwide...
, Symmetry Magazine and The New Yorker
The New Yorker
The New Yorker is an American magazine of reportage, commentary, criticism, essays, fiction, satire, cartoons and poetry published by Condé Nast...
.
Lisi's paper spawned a variety of reactions and debates across various physics blog
Blog
A blog is a type of website or part of a website supposed to be updated with new content from time to time. Blogs are usually maintained by an individual with regular entries of commentary, descriptions of events, or other material such as graphics or video. Entries are commonly displayed in...
s and online discussion groups. The first to comment was Sabine Hossenfelder, summarizing the paper and noting the lack of a dynamical symmetry breaking mechanism.
Luboš Motl
Luboš Motl
Luboš Motl is a Czech theoretical physicist who keeps a blog commenting on physics, global warming and politics. His scientific research concentrated on string theory, of which he has been a passionate defender. He proposed Matrix string theory in 1997.Motl was born in Plzeň, Czech Republic...
offered a colorful critique, objecting to the addition of bosons and fermions in Lisi's superconnection, and to the violation of the Coleman-Mandula theorem
Coleman-Mandula theorem
The Coleman–Mandula theorem, named after Sidney Coleman and Jeffrey Mandula, is a no-go theorem in theoretical physics. It states that "space-time and internal symmetries cannot be combined in any but a trivial way"...
. Further discussions, often including Lisi, took place on Peter Woit's
Peter Woit
Peter Woit is a Departmental Computer Administrator and Senior Lecturer in Discipline at Columbia University, known for his criticisms of string theory in his book Not Even Wrong, and his blog of the same name.-Career:...
Not Even Wrong, Sean Carroll's
Sean Carroll
Sean Carroll may refer to:*Sean B. Carroll , US evolutionary biologist*Sean M. Carroll , US theoretical physicist*Seán Carroll , Irish Sinn Féin politician...
Cosmic Variance, Steinn Sigurðsson's Dynamics of Cats, Physics Forums, Slashdot
Slashdot
Slashdot is a technology-related news website owned by Geeknet, Inc. The site, which bills itself as "News for Nerds. Stuff that Matters", features user-submitted and ‑evaluated current affairs news stories about science- and technology-related topics. Each story has a comments section...
, Digg
Digg
Digg is a social news website. Prior to Digg v4, its cornerstone function consisted of letting people vote stories up or down, called digging and burying, respectively. Digg's popularity prompted the creation of copycat social networking sites with story submission and voting systems...
, and Reddit
Reddit
reddit is a social news website where the registered users submit content, in the form of either a link or a text "self" post. Other users then vote the submission "up" or "down," which is used to rank the post and determine its position on the site's pages and front page.Reddit was originally...
. In the presentation "What's new at the arXiv?" on May 20, 2008, Simeon Warner stated that Lisi's paper is the most downloaded article on the arXiv. Among the physicists early to comment on E8 Theory, Sabine Hossenfelder, Peter Woit and Lee Smolin
Lee Smolin
Lee Smolin is an American theoretical physicist, a researcher at the Perimeter Institute for Theoretical Physics, and an adjunct professor of physics at the University of Waterloo. He is married to Dina Graser, a communications lawyer in Toronto. His brother is David M...
were generally supportive, while Luboš Motl and Jacques Distler
Jacques Distler
Jacques Distler is a physicist currently working in string theory. He has been a professor of physics at the University of Texas at Austin since 1994.-Early life and education:...
were critical.
On his blog, Musings, Jacques Distler offered one of the strongest criticisms of Lisi's approach, claiming to demonstrate that, unlike in the Standard Model, Lisi's model is nonchiral — consisting of a generation and an anti-generation — and to prove that any alternative embedding in E8 must be similarly nonchiral. These arguments were distilled in a paper written jointly with Skip Garibaldi, "There is no 'Theory of Everything' inside E8," published in Communications in Mathematical Physics
Communications in Mathematical Physics
Communications in Mathematical Physics is a peer-reviewed academic journal published by Springer. The journal publishes papers in all fields of mathematical physics, but focuses particularly in Analysis related to condensed matter physics, statistical mechanics and quantum field theory, and in...
. In this paper, Distler and Garibaldi offer a proof that it is impossible to embed all three generations of fermions in E8, or to obtain even the one-generation Standard Model. In a press release from his university, "Rock climber takes on surfer's theory," Garibaldi states that his article with Distler is a rebuttal of Lisi's theory. In response, Lisi argues that Distler and Garibaldi made unnecessary assumptions about how the embedding needs to happen. Addressing the one generation case, Lisi posted a new paper, "An Explicit Embedding of Gravity and the Standard Model in E8," describing how the algebra of gravity and the Standard Model with one generation of fermions embeds in the E8 Lie algebra explicitly using matrix representations. When this embedding is done, Lisi agrees that there is an antigeneration of fermions (also known as "mirror fermions") remaining in E8; but while Distler and Garibaldi state that these mirror fermions make the theory nonchiral, Lisi states that these mirror fermions might have high masses, making the theory chiral, or that they might be related to the other generations. Addressing the three generation case, Lisi agrees that three generations of fermions cannot be directly embedded in E8, but suggests that a gauge transformation related to triality
Triality
In mathematics, triality is a relationship between three vector spaces, analogous to the duality relation between dual vector spaces. Most commonly, it describes those special features of the Dynkin diagram D4 and the associated Lie group Spin, the double cover of 8-dimensional rotation group SO,...
might be used to relate the 64 mirror fermions and 64 other E8 generators to two other generations of 64 fermions.
The group blog, The n-Category Cafe, provides some of the more technical discussions, with posts by Lisi, Urs Schreiber, Kea, and Jacques Distler.
Sixteen arXiv preprints have cited Lisi's work. Lee Smolin
Lee Smolin
Lee Smolin is an American theoretical physicist, a researcher at the Perimeter Institute for Theoretical Physics, and an adjunct professor of physics at the University of Waterloo. He is married to Dina Graser, a communications lawyer in Toronto. His brother is David M...
's "The Plebanski action extended to a unification of gravity and Yang-Mills theory," December 6, 2007, proposes a symmetry breaking mechanism to go from an E8 symmetric action to Lisi's action for the Standard Model and gravity. Roberto Percacci's "Mixing internal and spacetime transformations: some examples and counterexamples" addresses a general loophole in the Coleman-Mandula theorem also thought to work in E8 Theory. Percacci and Fabrizio Nesti's "Chirality in unified theories of gravity" confirms the embedding of the algebra of gravitational and Standard Model forces acting on a generation of fermions in
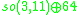, mentioning that Lisi's "ambitious attempt to unify all known fields into a single representation of E8 stumbled into chirality issues." Mathematician Bertram KostantBertram Kostant
-Early life and education:Kostant grew up in New York City, where he graduated from the celebrated Stuyvesant High School in 1945. He went on to obtain an undergraduate degree in mathematics from Purdue University in 1950. He earned his Ph.D...
discussed Lisi's work in a colloquium presentation at UC Riverside. In a joint paper with Lee Smolin and Simone Speziale, published in Journal of Physics A
Journal of Physics A
The Journal of Physics A: Mathematical and Theoretical is a peer-reviewed scientific journal published by IOP Publishing. It is part of the Journal of Physics series and covers theoretical physics focusing on sophisticated mathematical and computational techniques.The journal is divided into six...
, Lisi proposes a new action and symmetry breaking mechanism. In "An Explicit Embedding of Gravity and the Standard Model in E8," Lisi describes E8 Theory using explicit matrix representations.
On August 4, 2008, FQXi awarded Lisi a grant for further development of E8 Theory.
In September 2010 the popular magazine Scientific American reported on a conference in Banff inspired by Lisi's work. In December 2010 Scientific American published a feature article on E8 Theory, "A Geometric Theory of Everything." In May 2011 Lisi wrote a follow-up letter for Scientific American, describing criticism of E8 Theory and how it has progressed, noting that the theory is still incomplete, with the three generation issue remaining as a significant problem.
External links
- Deferential Geometry - Lisi's wiki, containing detailed mathematical background.
- Animation of E8 - a New Scientist video describing the theory using a visual representation.
- The Elementary Particle Explorer - an online E8 investigation tool for rotating and examining the particle assignments, charges, and interactions in the standard model and Lisi's E8 Theory.
- E8Flyer - an interactive E8 investigation tool based on the free Mathematica Notebook Player) (* see http://theoryofeverything.org/TOE/JGM/E8Favorites.pdf for screen shots *)
- An Exceptionally Technical Discussion of AESToE - a thread at "Physics Forums," started by Garrett Lisi, devoted to discussing the mathematics used in the AESToE paper.
- A beautiful new theory of everything - Lisi presents his theory at TEDTED (conference)TED is a global set of conferences owned by the private non-profit Sapling Foundation, formed to disseminate "ideas worth spreading"....
. - A Geometric Theory of Everything - a Scientific American article on E8 Theory.
- PDF version of "An Exceptionally Simple Theory of Everything" on Arxiv.org
- Webpage of "An Exceptionally Simple Theory of Everything" on Arxiv.org