
Artin group
Encyclopedia
In mathematics
, an Artin group (or generalized braid group) is a group
with a presentation
of the form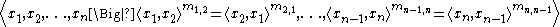
where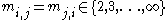 .
.
For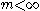 ,
, 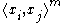 denotes an alternating product of
denotes an alternating product of 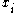 and
and 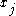 of length
of length  , beginning with
, beginning with 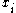 . For example,
. For example,
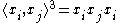
and
 .
.
If , then there is (by convention) no relation for
, then there is (by convention) no relation for  and
and 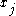 .
.
The integers can be organized into a symmetric matrix, known as the Coxeter matrix of the group. Each Artin group has as a quotient the Coxeter group
can be organized into a symmetric matrix, known as the Coxeter matrix of the group. Each Artin group has as a quotient the Coxeter group
with the same set of generators and Coxeter matrix. The kernel
of the homomorphism
to the associated Coxeter group, known as the pure Artin group, is generated by relations of the form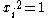 .
.
s are examples of Artin groups, with Coxeter matrix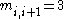 and
and 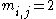 for
for  Several important classes of Artin groups can be defined in terms of the properties of the Coxeter matrix.
Several important classes of Artin groups can be defined in terms of the properties of the Coxeter matrix.
W = A(M) is finite, then the Artin group A = A(M) is called an Artin group of finite type. The 'irreducible types' are labeled as An , Bn = Cn , Dn , I2(n) , F4 , E6 , E7 , E8 , H3 , H4 .
A pure Artin group of finite type can be realized as the fundamental group
of the complement of a finite hyperplane arrangement in Cn. Pierre Deligne
and Brieskorn-Saito have used this geometric description to compute the center of A, its cohomology
, and to solve the word
and conjugacy
problems.
Γ on n vertices labeled 1, 2, …, n defines a matrix M, for which mij = 2 if i and j are connected by an edge in Γ, and mij = ∞ otherwise. The right-angled Artin group A(Γ) associated with the matrix M has n generators x1, x2, …, xn and relations
The class of right-angled Artin groups includes the free group
s of finite rank, corresponding to a graph with no edges, and the finitely-generated free abelian group
s, corresponding to a complete graph
. Mladen Bestvina and Noel Brady constructed a nonpositively curved cubical complex K whose fundamental group is a given right-angled Artin group A(Γ). They applied Morse-theoretic
arguments to their geometric description of Artin groups and exhibited first known examples of groups with the property (FP2) that are not finitely presented.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an Artin group (or generalized braid group) is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
with a presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
of the form
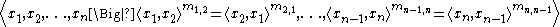
where
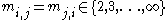 .
.For
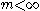 ,
, 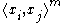 denotes an alternating product of
denotes an alternating product of 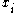 and
and 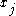 of length
of length  , beginning with
, beginning with 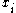 . For example,
. For example,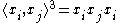
and
 .
.If
 , then there is (by convention) no relation for
, then there is (by convention) no relation for  and
and 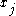 .
.The integers
 can be organized into a symmetric matrix, known as the Coxeter matrix of the group. Each Artin group has as a quotient the Coxeter group
can be organized into a symmetric matrix, known as the Coxeter matrix of the group. Each Artin group has as a quotient the Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
with the same set of generators and Coxeter matrix. The kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of the homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
to the associated Coxeter group, known as the pure Artin group, is generated by relations of the form
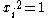 .
.Classes of Artin groups
Braid groupBraid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
s are examples of Artin groups, with Coxeter matrix
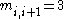 and
and 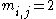 for
for  Several important classes of Artin groups can be defined in terms of the properties of the Coxeter matrix.
Several important classes of Artin groups can be defined in terms of the properties of the Coxeter matrix.Artin groups of finite type
If M is a Coxeter matrix of finite type, so that the corresponding Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
W = A(M) is finite, then the Artin group A = A(M) is called an Artin group of finite type. The 'irreducible types' are labeled as An , Bn = Cn , Dn , I2(n) , F4 , E6 , E7 , E8 , H3 , H4 .
A pure Artin group of finite type can be realized as the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the complement of a finite hyperplane arrangement in Cn. Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
and Brieskorn-Saito have used this geometric description to compute the center of A, its cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
, and to solve the word
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
and conjugacy
Conjugacy problem
In abstract algebra, the conjugacy problem for a group G with a given presentation is the decision problem of determining, given two words x and y in G, whether or not they represent conjugate elements of G...
problems.
Right-angled Artin groups
If M is a matrix all of whose elements are equal to 2 or ∞, then the corresponding Artin group is called a right-angled Artin group. For this class of Artin groups, a different labeling scheme is commonly used. Any graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
Γ on n vertices labeled 1, 2, …, n defines a matrix M, for which mij = 2 if i and j are connected by an edge in Γ, and mij = ∞ otherwise. The right-angled Artin group A(Γ) associated with the matrix M has n generators x1, x2, …, xn and relations
-
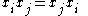 whenever i and j are connected by an edge in
whenever i and j are connected by an edge in 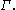
The class of right-angled Artin groups includes the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s of finite rank, corresponding to a graph with no edges, and the finitely-generated free abelian group
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
s, corresponding to a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
. Mladen Bestvina and Noel Brady constructed a nonpositively curved cubical complex K whose fundamental group is a given right-angled Artin group A(Γ). They applied Morse-theoretic
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
arguments to their geometric description of Artin groups and exhibited first known examples of groups with the property (FP2) that are not finitely presented.

