Canonical quantization
Encyclopedia
In physics
, canonical quantization is a procedure for quantizing
a classical theory while attempting to preserve the formal structure of the classical theory, to the extent possible. Historically, this was Werner Heisenberg
's route to obtaining quantum mechanics
. The word canonical arises from the Hamiltonian
approach to classical mechanics, in which a system's dynamics is generated via canonical Poisson brackets, a structure that is preserved to the extent possible in canonical quantization. This method was used in the context of quantum field theory
by Paul Dirac
, in his construction of quantum electrodynamics
. In the field theory context, it is also called second quantization, in contrast to the semi-classical first quantization
.
, wavefunctions by Erwin Schrödinger
. The connection between the two was discovered by Paul Dirac
, who was also the first to apply this technique to the quantization
of the electromagnetic field
. Eugene Wigner and Pascual Jordan
were the first to quantize the electron field, whose quantum mechanics was first investigated by Dirac
. The name canonical quantization may have been first coined by Pascual Jordan.
classic book on quantum mechanics.
In the classical mechanics
of a particle, there are dynamic variables which are called coordinates (
) and momenta (
). These specify the state of a classical system. The canonical structure (also known as the symplectic structure) of classical mechanics consists of Poisson bracket
s between these variables. All transformations which keep these brackets unchanged are allowed as canonical transformation
s in classical mechanics.
In quantum mechanics
, observables are represented by operators acting on a Hilbert space
of quantum states. The value of an operator on one of its eigenstates represents the value of a measurement. In particular, position and momentum are observables for a point particle, and are represented by quantum operators. An eigenvector of the position operator
representing a particle at position 
may be denoted by an element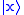 
of the Hilbert space, which satisfies 
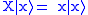. More general states may be constructed by superposition, e.g. 
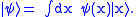The function 
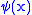is the wave function corresponding to this state in the Hilbert space, and may also be expressed as 
. The Poisson bracket
s of classical mechanics are replaced by commutator
s,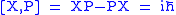
.
This construction leads to the uncertainty principle
in the form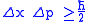
. This algebraic structure may be considered a quantum analog of the canonical structure of classical mechanics.
was successful at describing non-relativistic systems with fixed numbers of particles, but a new framework is needed to describe systems in which particles can be created or destroyed, for example, the electromagnetic field, considered as a collection of photons. It was eventually realized that special relativity
was inconsistent with single-particle quantum mechanics, so that all particles are now described relativistically by quantum fields. When the canonical quantization procedure is applied to quantum field theory
, the classical field
variable becomes a quantum operator. The amplitude of the field becomes quantized, and the quanta are identified with individual particles.
Historically, quantizing the classical theory of a single particle gave rise to a wavefunction. The classical equations of motion of a field are typically identical to the equation for the wave-function of one of its quanta. For example, the Klein-Gordon equation
is the classical equation of motion for a free scalar field, but also the quantum equation for a scalar particle wave-function. This meant that quantizing a field appeared to be similar to quantizing a theory that was already quantized, leading to the term second quantization in the early literature, which is still used to describe field quantization, even though the modern interpretation is different.
One drawback to canonical quantization for a relativistic field is that by relying on the Hamiltonian to determine time dependence, relativistic invariance is no longer manifest. Thus it is necessary to check that relativistic invariance is hidden, but not lost. Alternatively, the Feynman integral approach is available for quantizing relativistic fields, and is manifestly invariant. For non-relativistic field theories, such as those used in condensed matter physics
, this is not an issue.
. In general, all observables are constructed as operators on the Hilbert space, and the time-evolution of the operators is governed by the Hamiltonian
, which must be a positive operator. A state |0> annihilated by the Hamiltonian must be identified as the vacuum state
, which is the basis for building all other states. In a non-interacting (free) field theory, the vacuum is normally identified as a state containing zero particles. In a theory with interacting particles, identifying the vacuum is more subtle, due to vacuum polarization
, which implies that the physical vacuum in quantum field theory is never really empty. For further elaboration, see the articles on the quantum mechanical vacuum and the vacuum of quantum chromodynamics
. The details of the canonical quantization depend on the field being quantized, and whether it is free or interacting.
provides a good example of the canonical quantization procedure. For simplicity, the quantization can be carried in a 1+1 dimensional space-time
, in which the spatial direction is compactified to a circle of circumference 2π, rendering the momenta discrete. The classical Lagrangian
density is then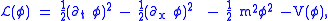
where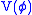
is a potential term, often taken to be a polynomial or monomial of degree 3 or higher. The action functional is
.
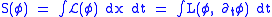The canonical momentum obtained via the Legendre transform using the action
is 
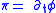, and the classical Hamiltonian
is found to be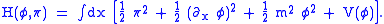
Canonical quantization treats the variables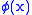
and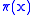 
as operators with canonical commutation relations at time 
given by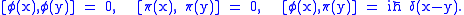
Operators constructed from
and 
can then formally be defined at other times via the time-evolution generated by the Hamiltonian: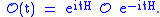
However, since
and 
do not commute, this expression is ambiguous at the quantum level. The problem is to construct a representation of the relevant operators 
on a Hilbert space
and to construct a positive operator 
as a quantum operator on this Hilbert space in such a way that it gives this evolution for the operators 
as given by the preceding equation, and to show that 
contains a vacuum state |0> on which 
has zero eigenvalue. In practice, this construction is a difficult problem for interacting field theories, and has been solved completely only in a few simple cases via the methods of constructive quantum field theory
. Many of these issues can be sidestepped using the Feynman integral as described for a particular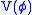
in the article on scalar field theory
.
In the case of a free field, with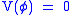
, the procedure is relatively straightforward. It is convenient to Fourier transform
the fields, so that
The reality of the fields imply that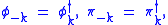
, and the commutation relations become 
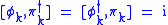, with all others vanishing. The Hamiltonian may be expanded in Fourier modes as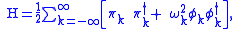
where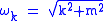
. The Hilbert space is constructed using creation and annihilation operators constructed from these modes,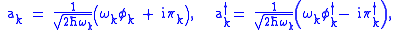
for which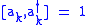
for all 
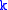, with all other commutators vanishing. The vacuum |0> is taken to be annihilated by all of the 
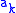, and 
is the Hilbert space constructed by applying any combination of the creation operators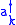 
to |0>. This Hilbert space is called Fock space
. For each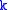
, this construction is identical to the quantum harmonic oscillator
. The quantum Hamiltonian can be defined to be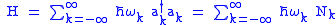
,
where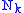
may be interpreted as the number operator giving the number of particles in a state with momentum 
.
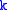This Hamiltonian differs from the previous expression by the subtraction of the zero-point energy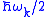
of each harmonic oscillator. This satisfies the condition that 
must annihilate the vacuum without affecting the time-evolution of operators via the above exponentiation operation. This subtraction of the zero-point energy may be considered to be a resolution of the quantum operator ordering ambiguity, since it is equivalent to requiring that all creation operators appear to the left of annihilation operators in the expansion of the Hamiltonian. This procedure is known as Wick ordering or normal ordering.
It turns out that commutation relations are useful only for quantizing bosons, for which the occupancy number of any state is unlimited. To quantize fermions, which satisfy the Pauli exclusion principle
, anti-commutators are needed. These are defined by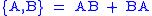
. When quantizing fermions, the fields are expanded in creation and annihilation operators 
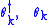which satisfy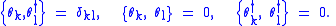
The states are constructed on a vacuum |0> annihilated by the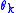
, and the Fock space
is built by applying all products of creation operators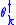
to |0>. Pauli's exclusion principle is satisfied because 
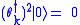due to the anti-commutation relations.
, so that the vacuum minimizing the Hamiltonian satisifes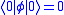 
, indicating that the vacuum expectation value
(VEV) of the field is zero. In cases involving spontaneous symmetry breaking
, it is possible to have a non-zero VEV, because the potential is minimized for a value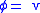
. This occurs for example, if 
and 
, for which the minimum energy is found at 
. The value of 
in one of these vacua may be considered a condensate of the field 
. Canonical quantization then can be carried out for the shifted field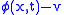 
, and particle states with respect to the shifted vacuum are defined by quantizing the shifted field. This construction is used in the Higgs mechanism
in the standard model
of particle physics
.
of spacetime
with the state at each slice being described by an element of a symplectic manifold
with the time evolution given by the symplectomorphism
generated by a Hamiltonian
function over the symplectic manifold. The quantum algebra of "operators" is an ħ-deformation of the algebra of smooth functions over the symplectic space such that the leading term in the Taylor expansion over ħ of the commutator
[A, B] is iħ{A, B}. (Here, the curly braces denote the Poisson bracket
. The subleading terms are all encoded in the Moyal bracket
, the suitable quantum deformation of the Poisson bracket.) In general, for the quantities (observables) involved,
and providing the arguments of such brackets, ħ-deformations are highly nonunique—quantization is an "art", and is specified by the physical context.
(Two different quantum systems may represent two different, inequivalent, deformations of the same classical limit, ħ → 0.)
Now, one looks for unitary representation
s of this quantum algebra. With respect to such a unitary representation, a symplectomorphism in the classical theory would now deform to a (metaplectic) unitary transformation
. In particular, the time evolution symplectomorphism generated by the classical Hamiltonian deforms to a unitary transformation generated by the corresponding quantum Hamiltonian.
A further generalization is to consider a Poisson manifold
instead of a symplectic space for the classical theory and perform an ħ-deformation of the corresponding Poisson algebra
or even Poisson supermanifold
s.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, canonical quantization is a procedure for quantizing
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
a classical theory while attempting to preserve the formal structure of the classical theory, to the extent possible. Historically, this was Werner Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
's route to obtaining quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. The word canonical arises from the Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
approach to classical mechanics, in which a system's dynamics is generated via canonical Poisson brackets, a structure that is preserved to the extent possible in canonical quantization. This method was used in the context of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
by Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, in his construction of quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
. In the field theory context, it is also called second quantization, in contrast to the semi-classical first quantization
First quantization
A first quantization of a physical system is a semi-classical treatment of quantum mechanics, in which particles or physical objects are treated using quantum wave functions but the surrounding environment is treated classically...
.
History
Commutators were introduced by Werner HeisenbergWerner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
, wavefunctions by Erwin Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
. The connection between the two was discovered by Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, who was also the first to apply this technique to the quantization
Quantization of the electromagnetic field
After quantization of the electromagnetic field, the EM field consists of discrete energy parcels, photons. Photons are massless particles of definite energy, definite momentum, and definite spin....
of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
. Eugene Wigner and Pascual Jordan
Pascual Jordan
-Further reading:...
were the first to quantize the electron field, whose quantum mechanics was first investigated by Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
. The name canonical quantization may have been first coined by Pascual Jordan.
Quantum mechanics
The following exposition is based largely on Dirac'sPaul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
classic book on quantum mechanics.
In the classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
of a particle, there are dynamic variables which are called coordinates (
) and momenta (). These specify the state of a classical system. The canonical structure (also known as the symplectic structure) of classical mechanics consists of Poisson bracketPoisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
s between these variables. All transformations which keep these brackets unchanged are allowed as canonical transformation
Canonical transformation
In Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates → that preserves the form of Hamilton's equations , although it...
s in classical mechanics.
In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, observables are represented by operators acting on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of quantum states. The value of an operator on one of its eigenstates represents the value of a measurement. In particular, position and momentum are observables for a point particle, and are represented by quantum operators. An eigenvector of the position operator
representing a particle at position may be denoted by an element 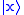of the Hilbert space, which satisfies 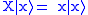. More general states may be constructed by superposition, e.g. 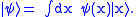The function 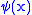is the wave function corresponding to this state in the Hilbert space, and may also be expressed as . The Poisson bracketPoisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
s of classical mechanics are replaced by commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
s,
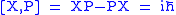.This construction leads to the uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
in the form
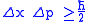. This algebraic structure may be considered a quantum analog of the canonical structure of classical mechanics.Second quantization: field theory
Quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
was successful at describing non-relativistic systems with fixed numbers of particles, but a new framework is needed to describe systems in which particles can be created or destroyed, for example, the electromagnetic field, considered as a collection of photons. It was eventually realized that special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
was inconsistent with single-particle quantum mechanics, so that all particles are now described relativistically by quantum fields. When the canonical quantization procedure is applied to quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the classical field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
variable becomes a quantum operator. The amplitude of the field becomes quantized, and the quanta are identified with individual particles.
Historically, quantizing the classical theory of a single particle gave rise to a wavefunction. The classical equations of motion of a field are typically identical to the equation for the wave-function of one of its quanta. For example, the Klein-Gordon equation
Klein-Gordon equation
The Klein–Gordon equation is a relativistic version of the Schrödinger equation....
is the classical equation of motion for a free scalar field, but also the quantum equation for a scalar particle wave-function. This meant that quantizing a field appeared to be similar to quantizing a theory that was already quantized, leading to the term second quantization in the early literature, which is still used to describe field quantization, even though the modern interpretation is different.
One drawback to canonical quantization for a relativistic field is that by relying on the Hamiltonian to determine time dependence, relativistic invariance is no longer manifest. Thus it is necessary to check that relativistic invariance is hidden, but not lost. Alternatively, the Feynman integral approach is available for quantizing relativistic fields, and is manifestly invariant. For non-relativistic field theories, such as those used in condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, this is not an issue.
Field operators
Quantum mechanically, fields are represented by operators on a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. In general, all observables are constructed as operators on the Hilbert space, and the time-evolution of the operators is governed by the Hamiltonian
Hamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
, which must be a positive operator. A state |0> annihilated by the Hamiltonian must be identified as the vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
, which is the basis for building all other states. In a non-interacting (free) field theory, the vacuum is normally identified as a state containing zero particles. In a theory with interacting particles, identifying the vacuum is more subtle, due to vacuum polarization
Vacuum polarization
In quantum field theory, and specifically quantum electrodynamics, vacuum polarization describes a process in which a background electromagnetic field produces virtual electron–positron pairs that change the distribution of charges and currents that generated the original electromagnetic...
, which implies that the physical vacuum in quantum field theory is never really empty. For further elaboration, see the articles on the quantum mechanical vacuum and the vacuum of quantum chromodynamics
QCD vacuum
The QCD vacuum is the vacuum state of quantum chromodynamics . It is an example of a non-perturbative vacuum state, characterized by many non-vanishing condensates such as the gluon condensate or the quark condensate...
. The details of the canonical quantization depend on the field being quantized, and whether it is free or interacting.
Real scalar field
A Scalar field theoryScalar field theory
In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
provides a good example of the canonical quantization procedure. For simplicity, the quantization can be carried in a 1+1 dimensional space-time
, in which the spatial direction is compactified to a circle of circumference 2π, rendering the momenta discrete. The classical LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
density is then
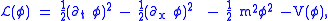
where
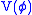is a potential term, often taken to be a polynomial or monomial of degree 3 or higher. The action functional is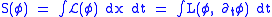.The canonical momentum obtained via the Legendre transform using the action
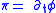is , and the classical HamiltonianHamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
is found to be
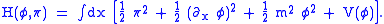
Canonical quantization treats the variables
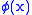and 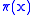as operators with canonical commutation relations at time given by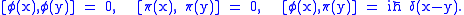Operators constructed from
and can then formally be defined at other times via the time-evolution generated by the Hamiltonian: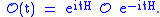However, since
and do not commute, this expression is ambiguous at the quantum level. The problem is to construct a representation of the relevant operators on a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and to construct a positive operator as a quantum operator on this Hilbert space in such a way that it gives this evolution for the operators as given by the preceding equation, and to show that contains a vacuum state |0> on which has zero eigenvalue. In practice, this construction is a difficult problem for interacting field theories, and has been solved completely only in a few simple cases via the methods of constructive quantum field theoryConstructive quantum field theory
In mathematical physics, constructive quantum field theory is the field devoted to showing that quantum theory is mathematically compatible with special relativity. This demonstration requires new mathematics, in a sense analogous to Newton developing calculus in order to understand planetary...
. Many of these issues can be sidestepped using the Feynman integral as described for a particular
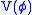in the article on scalar field theoryScalar field theory
In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
.
In the case of a free field, with
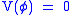, the procedure is relatively straightforward. It is convenient to Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
the fields, so that
The reality of the fields imply that
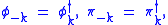, and the commutation relations become 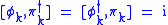, with all others vanishing. The Hamiltonian may be expanded in Fourier modes as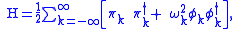where
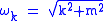. The Hilbert space is constructed using creation and annihilation operators constructed from these modes,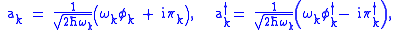for which
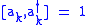for all 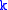, with all other commutators vanishing. The vacuum |0> is taken to be annihilated by all of the 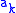, and is the Hilbert space constructed by applying any combination of the creation operators 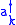to |0>. This Hilbert space is called Fock spaceFock space
The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...
. For each
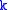, this construction is identical to the quantum harmonic oscillatorQuantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
. The quantum Hamiltonian can be defined to be
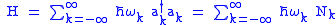,where
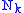may be interpreted as the number operator giving the number of particles in a state with momentum 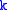.This Hamiltonian differs from the previous expression by the subtraction of the zero-point energy
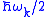of each harmonic oscillator. This satisfies the condition that must annihilate the vacuum without affecting the time-evolution of operators via the above exponentiation operation. This subtraction of the zero-point energy may be considered to be a resolution of the quantum operator ordering ambiguity, since it is equivalent to requiring that all creation operators appear to the left of annihilation operators in the expansion of the Hamiltonian. This procedure is known as Wick ordering or normal ordering.Other fields
All other fields can be quantized by a generalization of this procedure. Vector or tensor fields simply have more components, and independent creation and destruction operators must be introduced for each independent component. If a field has any internal symmetry, then creation and destruction operators must be introduced for each component of the field related to this symmetry as well. If there is a gauge symmetry, then the number of independent components of the field must be carefully analyzed to avoid over-counting equivalent configurations, and gauge-fixing may be applied if needed.It turns out that commutation relations are useful only for quantizing bosons, for which the occupancy number of any state is unlimited. To quantize fermions, which satisfy the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
, anti-commutators are needed. These are defined by
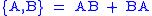. When quantizing fermions, the fields are expanded in creation and annihilation operators 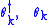which satisfy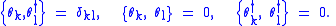The states are constructed on a vacuum |0> annihilated by the
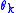, and the Fock spaceFock space
The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...
is built by applying all products of creation operators
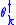to |0>. Pauli's exclusion principle is satisfied because 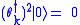due to the anti-commutation relations.Condensates
The construction of the scalar field states above assumed that the potential was minimized at, so that the vacuum minimizing the Hamiltonian satisifes 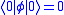, indicating that the vacuum expectation valueVacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
(VEV) of the field is zero. In cases involving spontaneous symmetry breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
, it is possible to have a non-zero VEV, because the potential is minimized for a value
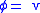. This occurs for example, if and , for which the minimum energy is found at . The value of in one of these vacua may be considered a condensate of the field . Canonical quantization then can be carried out for the shifted field 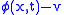, and particle states with respect to the shifted vacuum are defined by quantizing the shifted field. This construction is used in the Higgs mechanismHiggs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
in the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
.
Mathematical quantization
The classical theory is described using a spacelike foliationFoliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
with the state at each slice being described by an element of a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
with the time evolution given by the symplectomorphism
Symplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
generated by a Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
function over the symplectic manifold. The quantum algebra of "operators" is an ħ-deformation of the algebra of smooth functions over the symplectic space such that the leading term in the Taylor expansion over ħ of the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
[A, B] is iħ{A, B}. (Here, the curly braces denote the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
. The subleading terms are all encoded in the Moyal bracket
Moyal bracket
In physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
, the suitable quantum deformation of the Poisson bracket.) In general, for the quantities (observables) involved,
and providing the arguments of such brackets, ħ-deformations are highly nonunique—quantization is an "art", and is specified by the physical context.
(Two different quantum systems may represent two different, inequivalent, deformations of the same classical limit, ħ → 0.)
Now, one looks for unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s of this quantum algebra. With respect to such a unitary representation, a symplectomorphism in the classical theory would now deform to a (metaplectic) unitary transformation
Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
. In particular, the time evolution symplectomorphism generated by the classical Hamiltonian deforms to a unitary transformation generated by the corresponding quantum Hamiltonian.
A further generalization is to consider a Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
instead of a symplectic space for the classical theory and perform an ħ-deformation of the corresponding Poisson algebra
Poisson algebra
In mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
or even Poisson supermanifold
Poisson supermanifold
In differential geometry a Poisson supermanifold is a differential supermanifold M such that the supercommutative algebra of smooth functions over it , C^\infty is equipped with a bilinear map called the Poisson superbracket turning it into a Poisson superalgebra.Every...
s.
See also
- Correspondence principleCorrespondence principleIn physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
- Creation and annihilation operatorsCreation and annihilation operatorsCreation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
- Dirac bracketDirac bracketThe Dirac bracket is a generalization of the Poisson bracket developed by Paul Dirac to correctly treat systems with second class constraints in Hamiltonian mechanics and canonical quantization. It is an important part of Dirac's development of Hamiltonian mechanics to handle more general Lagrangians...
- Moyal bracketMoyal bracketIn physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
- Weyl quantizationWeyl quantizationIn mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
Historical References
- Silvan S. Schweber: QED and the men who made it, Princeton Univ. Press, 1994, ISBN 0-691-03327-7
General Technical References
- James D. Bjorken, Sidney D. Drell: Relativistic quantum mechanics, New York, McGraw-Hill, 1964
- Alexander Altland, Ben Simons: Condensed matter field theory, Cambridge Univ. Press, 2009, ISBN 978-0-521-84508-3
- Franz Schwabl: Advanced Quantum Mechanics, Berlin and elsewhere, Springer, 2009 ISBN 978-3-540-85061-8
- An introduction to quantum field theory, by M.E.Peskin and H.D.Schroeder, ISBN 0-201-50397-2
External links
- What is "Relativistic Canonical Quantization"?
- Pedagogic Aides to Quantum Field Theory Click on the links for Chaps. 1 and 2 at this site to find an extensive, simplified introduction to second quantization. See Sect. 1.5.2 in Chap. 1. See Sect. 2.7 and the chapter summary in Chap. 2.