
Examples of vector spaces
Encyclopedia
This page lists some examples of vector spaces. See vector space
for the definitions of terms used on this page. See also: dimension
, basis
.
Notation. We will let F denote an arbitrary field
such as the real number
s R or the complex number
s C. See also: table of mathematical symbols
.
s). Both vector addition and scalar multiplication are trivial. A basis
for this vector space is the empty set
, so that {0} is the 0-dimensional vector space over F. Every vector space over F contains a subspace isomorphic to this one.
Do not confuse this space with the null space
of a linear operator F, which is the kernel of F.
The field is a rather special vector space; in fact it is the simplest example of a commutative algebra
over F. Also, F has just two subspaces
: {0} and F itself.
n, the space of all n-tuples of elements of F forms an n-dimensional vector space over F sometimes called coordinate space
and denoted Fn. An element of Fn is written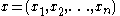
where each xi is an element of F. The operations on Fn are defined by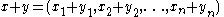
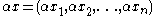
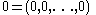

The most common cases are where F is the field of real number
s giving the real coordinate space Rn, or the field of complex number
s giving the complex coordinate space Cn.
The quaternion
s and the octonion
s are respectively four- and eight- dimensional vector spaces over the reals.
The vector space Fn comes with a standard basis
: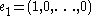
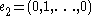
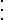
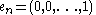
where 1 denotes the multiplicative identity in F.

then only a finite number of the xi are nonzero (i.e., the coordinates become all zero after a certain point). Addition and scalar multiplication are given as in finite coordinate space. The dimensionality of F∞ is countably infinite. A standard basis consists of the vectors ei which contain a 1 in the i-th slot and zeros elsewhere. This vector space is the coproduct
(or direct sum
) of countably many copies of the vector space F.
Note the role of the finiteness condition here. One could consider arbitrary sequences of elements in F, which also constitute a vector space with the same operations, often denoted by FN - see below. FN is the product
of countably many copies of F.
By Zorn's lemma, FN has a basis (there is no obvious basis). There are uncountably infinite elements in the basis. Since the dimensions are different, FN is not isomorphic to F∞. It is worth noting that FN is (isomorphic to) the dual space
of F∞, because a linear map T from F∞ to F is determined uniquely by its values T(ei) on the basis elements of F∞, and these values can be arbitrary. Thus one sees that a vector space need not be isomorphic to its dual if it is infinite dimensional, in contrast to the finite dimensional case.
with entries in F. Then Fm×n is a vector space over F. Vector addition is just matrix addition and scalar multiplication is defined in the obvious way (by multiplying each entry by the same scalar). The zero vector is just the zero matrix. The dimension
of Fm×n is mn. One possible choice of basis is the matrices with a single entry equal to 1 and all other entries 0.
s with coefficients in F is vector space over F denoted F[x]. Vector addition and scalar multiplication are defined in the obvious manner. If the degree
of the polynomials is unrestricted then the dimension of F[x] is countably infinite. If instead one restricts to polynomials with degree less than or equal to n, then we have a vector space with dimension n+1.
One possible basis for F[x] is a monomial basis
: the coordinates of a polynomial with respect to this basis are its coefficient
s, and the map sending a polynomial to the sequence of its coefficients is a linear isomorphism from F[x] to the infinite coordinate space F∞.
The vector space of polynomials with real coefficients and degree less than or equal to n is denoted by Pn.
s in several variables with coefficients in F is vector space over F denoted F[x1, x2, …, xr]. Here r is the number of variables.
Let X be an arbitrary set and V an arbitrary vector space over F. The space of all function
s from X to V is a vector space over F under pointwise
addition and multiplication. That is, let f : X → V and g : X → V denote two functions, and let α∈F. We define
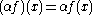
where the operations on the right hand side are those in V. The zero vector is given by the constant function sending everything to the zero vector in V. The space of all functions from X to V is commonly denoted VX.
If X is finite and V is finite-dimensional then VX has dimension |X|(dim V), otherwise the space is infinite-dimensional (uncountably so if X is infinite).
Many of the vector spaces that arise in mathematics are subspaces of some function space. We give some further examples.
The space described above is commonly denoted (FX)0 and is called generalized coordinate space for the following reason. If X is the set of numbers between 1 and n then this space is easily seen to be equivalent to the coordinate space Fn. Likewise, if X is the set of natural number
s, N, then this space is just F∞.
A canonical basis for (FX)0 is the set of functions {δx | x ∈ X} defined by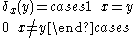
The dimension of (FX)0 is therefore equal to the cardinality of X. In this manner we can construct a vector space of any dimension over any field. Furthermore, every vector space is isomorphic to one of this form. Any choice of basis determines an isomorphism by sending the basis onto the canonical one for (FX)0.
Generalized coordinate space may also be understood as the direct sum
of |X| copies of F (i.e. one for each point in X):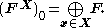
The finiteness condition is built into the definition of the direct sum. Contrast this with the direct product
of |X| copies of F which would give the full function space FX.
itself is the vector space of linear maps. Let L(V,W) denote the set of all linear maps from V to W (both of which are vector spaces over F). Then L(V,W) is a subspace of WV since it is closed under addition and scalar multiplication.
Note that L(Fn,Fm) can be identified with the space of matrices Fm×n in a natural way. In fact, by choosing appropriate bases for finite-dimensional spaces V and W, L(V,W) can also be identified with Fm×n. This identification normally depends on the choice of basis.
, such as the unit interval
[0,1], we can consider the space of all continuous function
s from X to R. This is a vector subspace of RX since the sum of any two continuous functions is continuous and scalar multiplication is continuous.
is a subspace of RR if the equation is linear. This is because differentiation
is a linear operation, i.e.,(a f + b g)' = a f' + b g', where ' is the differentiation operator.
). Then F can be regarded as a vector space over K by restricting scalar multiplication to elements in K (vector addition is defined as normal). The dimension of this vector space is called the degree of the extension. For example the complex number
s C form a two dimensional vector space over the real numbers R. Likewise, the real numbers R form an (uncountably) infinite-dimensional vector space over the rational number
s Q.
If V is a vector space over F it may also be regarded as vector space over K. The dimensions are related by the formula
For example Cn, regarded as a vector space over the reals, has dimension 2n.
and the vector space has a finite dimension. Thus we have Fq, the unique finite field (up to isomorphism
, of course) with q elements. Here q must be a power of a prime
(q = pm with p prime). Then any n-dimensional vector space V over Fq will have qn elements. Note that the number of elements in V is also the power of a prime. The primary example of such a space is the coordinate space (Fq)n.
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
for the definitions of terms used on this page. See also: dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
, basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
.
Notation. We will let F denote an arbitrary field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
such as the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R or the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C. See also: table of mathematical symbols
Table of mathematical symbols
This is a listing of common symbols found within all branches of mathematics. Each symbol is listed in both HTML, which depends on appropriate fonts being installed, and in , as an image.-Symbols:-Variations:...
.
Trivial or zero vector space
The simplest example of a vector space is the trivial one: {0}, which contains only the zero vector (see axiom 3 of vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s). Both vector addition and scalar multiplication are trivial. A basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for this vector space is the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, so that {0} is the 0-dimensional vector space over F. Every vector space over F contains a subspace isomorphic to this one.
Do not confuse this space with the null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of a linear operator F, which is the kernel of F.
Field
The next simplest example is the field F itself. Vector addition is just field addition and scalar multiplication is just field multiplication. Any non-zero element of F serves as a basis so F is a 1-dimensional vector space over itself.The field is a rather special vector space; in fact it is the simplest example of a commutative algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
over F. Also, F has just two subspaces
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
: {0} and F itself.
Coordinate space
Perhaps the most important example of a vector space is the following. For any positive integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n, the space of all n-tuples of elements of F forms an n-dimensional vector space over F sometimes called coordinate space
Coordinate space
In mathematics, specifically in linear algebra, the coordinate space, Fn, is the prototypical example of an n-dimensional vector space over a field F. It can be defined as the product space of F over a finite index set.-Definition:...
and denoted Fn. An element of Fn is written
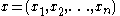
where each xi is an element of F. The operations on Fn are defined by
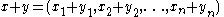
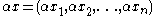
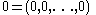

The most common cases are where F is the field of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s giving the real coordinate space Rn, or the field of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s giving the complex coordinate space Cn.
The quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s and the octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s are respectively four- and eight- dimensional vector spaces over the reals.
The vector space Fn comes with a standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
:
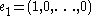
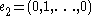
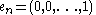
where 1 denotes the multiplicative identity in F.
Infinite coordinate space
Let F∞ denote the space of infinite sequences of elements from F such that only finitely many elements are nonzero. That is, if we write an element of F∞ as
then only a finite number of the xi are nonzero (i.e., the coordinates become all zero after a certain point). Addition and scalar multiplication are given as in finite coordinate space. The dimensionality of F∞ is countably infinite. A standard basis consists of the vectors ei which contain a 1 in the i-th slot and zeros elsewhere. This vector space is the coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
(or direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
) of countably many copies of the vector space F.
Note the role of the finiteness condition here. One could consider arbitrary sequences of elements in F, which also constitute a vector space with the same operations, often denoted by FN - see below. FN is the product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
of countably many copies of F.
By Zorn's lemma, FN has a basis (there is no obvious basis). There are uncountably infinite elements in the basis. Since the dimensions are different, FN is not isomorphic to F∞. It is worth noting that FN is (isomorphic to) the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of F∞, because a linear map T from F∞ to F is determined uniquely by its values T(ei) on the basis elements of F∞, and these values can be arbitrary. Thus one sees that a vector space need not be isomorphic to its dual if it is infinite dimensional, in contrast to the finite dimensional case.
Product of vector spaces
Starting from n vector spaces, or a countably infinite collection of them, each with the same field, we can define the product space like above.Matrices
Let Fm×n denote the set of matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with entries in F. Then Fm×n is a vector space over F. Vector addition is just matrix addition and scalar multiplication is defined in the obvious way (by multiplying each entry by the same scalar). The zero vector is just the zero matrix. The dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of Fm×n is mn. One possible choice of basis is the matrices with a single entry equal to 1 and all other entries 0.
One variable
The set of polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s with coefficients in F is vector space over F denoted F[x]. Vector addition and scalar multiplication are defined in the obvious manner. If the degree
Degree (mathematics)
In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
of the polynomials is unrestricted then the dimension of F[x] is countably infinite. If instead one restricts to polynomials with degree less than or equal to n, then we have a vector space with dimension n+1.
One possible basis for F[x] is a monomial basis
Monomial basis
In mathematics a monomial basis is a way to describe uniquely a polynomial using a linear combination of monomials. This description, the monomial form of a polynomial, is often used because of the simple structure of the monomial basis....
: the coordinates of a polynomial with respect to this basis are its coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s, and the map sending a polynomial to the sequence of its coefficients is a linear isomorphism from F[x] to the infinite coordinate space F∞.
The vector space of polynomials with real coefficients and degree less than or equal to n is denoted by Pn.
Several variables
The set of polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in several variables with coefficients in F is vector space over F denoted F[x1, x2, …, xr]. Here r is the number of variables.
- See also: polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
Function spaces
- See main article at Function spaceFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
, especially the functional analysis section.
Let X be an arbitrary set and V an arbitrary vector space over F. The space of all function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s from X to V is a vector space over F under pointwise
Pointwise
In mathematics, the qualifier pointwise is used to indicate that a certain property is defined by considering each value f of some function f. An important class of pointwise concepts are the pointwise operations — operations defined on functions by applying the operations to function values...
addition and multiplication. That is, let f : X → V and g : X → V denote two functions, and let α∈F. We define

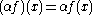
where the operations on the right hand side are those in V. The zero vector is given by the constant function sending everything to the zero vector in V. The space of all functions from X to V is commonly denoted VX.
If X is finite and V is finite-dimensional then VX has dimension |X|(dim V), otherwise the space is infinite-dimensional (uncountably so if X is infinite).
Many of the vector spaces that arise in mathematics are subspaces of some function space. We give some further examples.
Generalized coordinate space
Let X be an arbitrary set. Consider the space of all functions from X to F which vanish on all but a finite number of points in X. This space is a vector subspace of FX, the space of all possible functions from X to F. To see this note that the union of two finite sets is finite so that the sum of two functions in this space will still vanish outside a finite set.The space described above is commonly denoted (FX)0 and is called generalized coordinate space for the following reason. If X is the set of numbers between 1 and n then this space is easily seen to be equivalent to the coordinate space Fn. Likewise, if X is the set of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, N, then this space is just F∞.
A canonical basis for (FX)0 is the set of functions {δx | x ∈ X} defined by
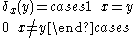
The dimension of (FX)0 is therefore equal to the cardinality of X. In this manner we can construct a vector space of any dimension over any field. Furthermore, every vector space is isomorphic to one of this form. Any choice of basis determines an isomorphism by sending the basis onto the canonical one for (FX)0.
Generalized coordinate space may also be understood as the direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of |X| copies of F (i.e. one for each point in X):
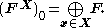
The finiteness condition is built into the definition of the direct sum. Contrast this with the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of |X| copies of F which would give the full function space FX.
Linear maps
An important example arising in the context of linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
itself is the vector space of linear maps. Let L(V,W) denote the set of all linear maps from V to W (both of which are vector spaces over F). Then L(V,W) is a subspace of WV since it is closed under addition and scalar multiplication.
Note that L(Fn,Fm) can be identified with the space of matrices Fm×n in a natural way. In fact, by choosing appropriate bases for finite-dimensional spaces V and W, L(V,W) can also be identified with Fm×n. This identification normally depends on the choice of basis.
Continuous functions
If X is some topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, such as the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1], we can consider the space of all continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s from X to R. This is a vector subspace of RX since the sum of any two continuous functions is continuous and scalar multiplication is continuous.
Differential equations
The subset of the space of all functions from R to R consisting of (sufficiently differentiable) functions that satisfy a certain differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
is a subspace of RR if the equation is linear. This is because differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
is a linear operation, i.e.,
Field extensions
Suppose K is a subfield of F (cf. field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
). Then F can be regarded as a vector space over K by restricting scalar multiplication to elements in K (vector addition is defined as normal). The dimension of this vector space is called the degree of the extension. For example the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C form a two dimensional vector space over the real numbers R. Likewise, the real numbers R form an (uncountably) infinite-dimensional vector space over the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q.
If V is a vector space over F it may also be regarded as vector space over K. The dimensions are related by the formula
- dimKV = (dimFV)(dimKF)
For example Cn, regarded as a vector space over the reals, has dimension 2n.
Finite vector spaces
Apart from the trivial case of a zero-dimensional space over any field, a vector space over a field F has a finite number of elements if and only if F is a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
and the vector space has a finite dimension. Thus we have Fq, the unique finite field (up to isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, of course) with q elements. Here q must be a power of a prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
(q = pm with p prime). Then any n-dimensional vector space V over Fq will have qn elements. Note that the number of elements in V is also the power of a prime. The primary example of such a space is the coordinate space (Fq)n.

