History of geodesy
Encyclopedia
Geodesy[1] also named geodetics, is the scientific discipline that deals with the measurement and representation of the Earth.
Humanity has always been interested in the Earth
. During very early times this interest was limited, naturally, to the immediate vicinity of home and residency, and the fact that we live on a near spherical globe may or may not have been apparent. As humanity developed, so did its interest in understanding and mapping the size, shape, and composition of the Earth.
), and the heavens a physical dome spanning over it. Two early arguments for a spherical earth were that lunar eclipses were seen as circular shadows which could only be caused by a spherical Earth, and that Polaris
is seen lower in the sky as one travels South.
The early Greeks
, in their speculation and theorizing, ranged from the flat disc advocated by Homer
to the spherical body postulated by Pythagoras
— an idea supported one hundred years later by Aristotle
. Pythagoras was a mathematician and to him the most perfect figure was a sphere
. He reasoned that the gods would create a perfect figure and therefore the earth was created to be spherical in shape. Anaximenes
, an early Greek scientist, believed strongly that the earth was rectangular in shape.
Since the spherical shape was the most widely supported during the Greek Era, efforts to determine its size followed. Plato
determined the circumference of the earth to be 400,000 stadia (between 62,800 km/39,250 mi and 74,000 km/46,250 mi ) while Archimedes
estimated 300,000 stadia ( 55,500 kilometre
s/34,687 mile
s ), using the Hellenic stadia which scholars generally take to be 185 meters or 1/10 of a geographical mile
. Plato's figure was a guess and Archimedes' a more conservative approximation.
(276 BC– 195 BC), is said to have made more explicit measurements. He had heard that on the longest day of the summer solstice
, the midday sun shone to the bottom of a well in the town of Syene (Aswan
). At the same time, he observed the sun was not directly overhead at Alexandria
; instead, it cast a shadow with the vertical equal to 1/50th of a circle (7° 12'). To these observations, Eratosthenes applied certain "known" facts (1) that on the day of the summer solstice, the midday sun was directly over the Tropic of Cancer
; (2) Syene was on this tropic; (3) Alexandria and Syene lay on a direct north-south line; (4) The sun was a relatively long way away (Astronomical unit
). Legend has it that he had someone walk from Alexandria to Syene to measure the distance: that came out to be equal to 5000 stadia or (at the usual Hellenic 185 meters per stadion) about 925 kilometres.
From these observations, measurements, and/or "known" facts, Eratosthenes concluded that, since the angular deviation of the sun from the vertical direction
at Alexandria was also the angle of the subtended arc (see illustration), the linear distance between Alexandria and Syene was 1/50 of the circumference of the Earth which thus must be 50×5000 = 250,000 stadia or probably 25,000 geographical miles. The circumference of the Earth is 24,902 miles (40,075.16 km). Over the poles it is more precisely 40,008 km or 24,860 statute miles. The actual unit of measure used by Eratosthenes was the stadion. No one knows for sure what his stadion equals in today's units, but most current specialists in antiquities accept that it was the regular Hellenic 185 meter stadion, and few if any would incline to an obscure definition that happened to make Eratosthenes's result correct.
Had the experiment been carried out as described, it would not be remarkable if it agreed with actuality. What is remarkable is that the result was probably about one sixth too high. His measurements were subject to several inaccuracies: (1) though at the summer solstice the noon sun is overhead at the Tropic of Cancer, Syene was not exactly on the tropic (which was at 23° 43' latitude in that day) but about 22 geographical miles to the north; (2) the difference of latitude between Alexandria (31.2 degrees north latitude) and Syene (24.1 degrees) is really 7.1 degrees rather than the perhaps rounded (1/50 of a circle) value of 7° 12' that Eratosthenes used; (4) the actual solstice zenith distance of the noon sun at Alexandria was 31° 12' − 23° 43' = 7° 29' or about 1/48 of a circle not 1/50 = 7° 12', an error closely consistent with use of a vertical gnomon
which fixes not the sun's center but the solar upper limb
16' higher; (5) the most importantly flawed element, whether he measured or adopted it, was the latitudinal distance from Alexandria to Syene (or the true Tropic somewhat further south) which he appears to have overestimated by a factor that relates to most of the error in his resulting circumference of the earth.
A parallel later legendary ancient measurement of the size of the earth was made by another influential Greek scholar, Posidonius
. He is said to have noted that the star Canopus
was hidden from view in most parts of Greece but that it just grazed the horizon at Rhodes. Posidonius is supposed to have measured the elevation of Canopus at Alexandria and determined that the angle was 1/48th of circle. He assumed the distance from Alexandria to Rhodes to be 5000 stadia, and so he computed the Earth's circumference in stadia as 48 times 5000 = 240,000. Some scholars see these results as luckily semi-accurate due to cancellation of errors. But since the Canopus observations are both mistaken by over a degree, the "experiment" may be not much more than a recycling of Eratosthenes's numbers, while altering 1/50 to the correct 1/48 of a circle. Later either he or a follower appears to have altered the base distance to agree with Eratosthenes's Alexandria-to-Rhodes figure of 3750 stadia since Posidonius's final circumference was 180,000 stadia, which equals 48×3750 stadia. The 180,000 stadia circumference of Posidonius is suspiciously close to that which results from another unlaborious method of measuring the earth, by timing ocean sun-sets from different heights, a method which produces a size of the earth too low by a factor of 5/6, again due to horizontal refraction.
The abovementioned larger and smaller sizes of the earth were those used by Claudius Ptolemy at different times, 252,000 stadia in the Almagest
and 180,000 stadia in the later Geographical Directory. His midcareer conversion resulted in the latter work's systematic exaggeration of degree longitudes in the Mediterranean by a factor close to the ratio of the two seriously differing sizes discussed here, which indicates that the conventional size of the earth was what changed, not the stadion.
(AD 476 - 550) was a pioneer of mathematical astronomy. He describes the earth as being spherical and that it rotates on its axis, among other things in his work Āryabhaṭīya
. Aryabhatiya is divided into four sections. Gitika, Ganitha (mathematics), Kalakriya (reckoning of time) and Gola (celestial sphere
). The discovery that the earth rotates on its own axis from west to east is described in Aryabhatiya ( Gitika 3,6; Kalakriya 5; Gola 9,10;). For example he explained the apparent motion of heavenly bodies is only an illusion (Gola 9), with the following simile;
Aryabhatiya also estimates the circumference of Earth, accurate to 1% which is remarkable. Aryabhata gives the radius of planets in terms of the Earth-Sun distance as essentially their periods of rotation around the Sun. He also gave the correct explanation of lunar and solar eclipses and that the Moon shines by reflecting sunlight.
theory, used it to calculate the distance and direction from any given point on the earth to Mecca
. This determined the Qibla
, or Muslim direction of prayer. Muslim mathematicians
developed spherical trigonometry
which was used in these calculations.
Around AD 830 Caliph al-Ma'mun
commissioned a group of astronomers to measure the distance from Tadmur (Palmyra
) to al-Raqqah
, in modern Syria
. They found the cities to be separated by one degree of latitude and the distance between them to be 66 2/3 miles and thus calculated the Earth's circumference to be 24,000 miles. Another estimate given was 56 2/3 Arabic miles per degree, which corresponds to 111.8 km per degree and a circumference of 40,248 km, very close to the currently modern values of 111.3 km per degree and 40,068 km circumference, respectively.
Muslim astronomers
and geographers were aware of magnetic declination
by the 15th century, when the Egyptian Muslim astronomer 'Izz al-Din al-Wafa'i (d. 1469/1471) measured it as 7 degrees from Cairo
.
At the age of 17, Biruni calculated the latitude
of Kath, Khwarazm, using the maximum altitude of the Sun. Biruni also solved a complex geodesic equation in order to accurately compute the Earth
's circumference
, which were close to modern values of the Earth's circumference. His estimate of 6,339.9 km for the Earth radius
was only 16.8 km less than the modern value of 6,356.7 km. In contrast to his predecessors who measured the Earth's circumference by sighting the Sun simultaneously from two different locations, Biruni developed a new method of using trigonometric calculations based on the angle between a plain
and mountain
top which yielded more accurate measurements of the Earth's circumference and made it possible for it to be measured by a single person from a single location. Abu Rayhan Biruni's method was intended to avoid "walking across hot, dusty deserts" and the idea came to him when he was on top of a tall mountain in India. From the top of the mountain, he sighted the dip angle which, along with the mountain's height (which he calculated beforehand), he applied to the law of sines
formula. This was the earliest known use of dip angle and the earliest practical use of the law of sines. He also made use of algebra
to formulate trigonometric equations and used the astrolabe
to measure angles. His method can be summarized as follows:
He first calculated the height of the mountain by going to two points at sea level with a known distance apart and then measuring the angle between the plain and the top of the mountain for both points. He made both the measurements using an astrolabe. He then used the following trigonometric formula relating the distance (d) between both points with the tangents of their angles (θ) to determine the height (h) of the mountain:
He then stood at the highest point of the mountain, where he measured the dip angle using an astrolabe. He applied the values he obtained for the dip angle and the mountain's height to the following trigonometric formula in order to calculate the Earth's radius:
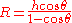
where
Biruni had also, by the age of 22, written a study of map projection
s, Cartography
, which included a method for projecting a hemisphere
on a plane
. Around 1025, Biruni was the first to describe a polar equi-azimuthal equidistant projection
of the celestial sphere
. He was also regarded as the most skilled when it came to mapping cities and measuring the distances between them, which he did for many cities in the Middle East
and western Indian subcontinent
. He often combined astronomical readings and mathematical equations, in order to develop methods of pin-pointing locations by recording degrees of latitude and longitude
. He also developed similar techniques when it came to measuring the heights of mountains, depths of valley
s, and expanse of the horizon, in The Chronology of the Ancient Nations. He also discussed human geography
and the planetary habitability
of the Earth. He hypothesized that roughly a quarter of the Earth's surface is habitable by humans, and also argued that the shores of Asia and Europe were "separated by a vast sea, too dark and dense to navigate and too risky to try".
through his world maps. The maps of Ptolemy strongly influenced the cartographers of the Middle Ages
. It is probable that Christopher Columbus
, using such maps, was led to believe that Asia was only 3 or 4 thousand miles west of Europe.
Ptolemy's view was not universal, however, and chapter 20 of Mandeville's Travels (c. 1357) supports Erasthenes' calculation.
It was not until the 16th century that his concept of the Earth's size was revised. During that period the Flemish cartographer, Mercator
, made successive reductions in the size of the Mediterranean Sea
and all of Europe which had the effect of increasing the size of the earth.
and the theodolite
and the development of logarithm tables allowed exact triangulation
and grade measurement
.
performed the first modern meridian arc
measurement in 1699–70. He measured a base line
by the aid of wooden rods, used a telescope in his angle measurements, and computed with logarithms. Jacques Cassini
later continued Picard's arc northward to Dunkirk and southward to the Spanish boundary. Cassini divided the measured arc into two parts, one northward from Paris
, another southward. When he computed the length of a degree from both chains, he found that the length of one degree in the northern part of the chain was shorter than that in the southern part. See the illustration at right.
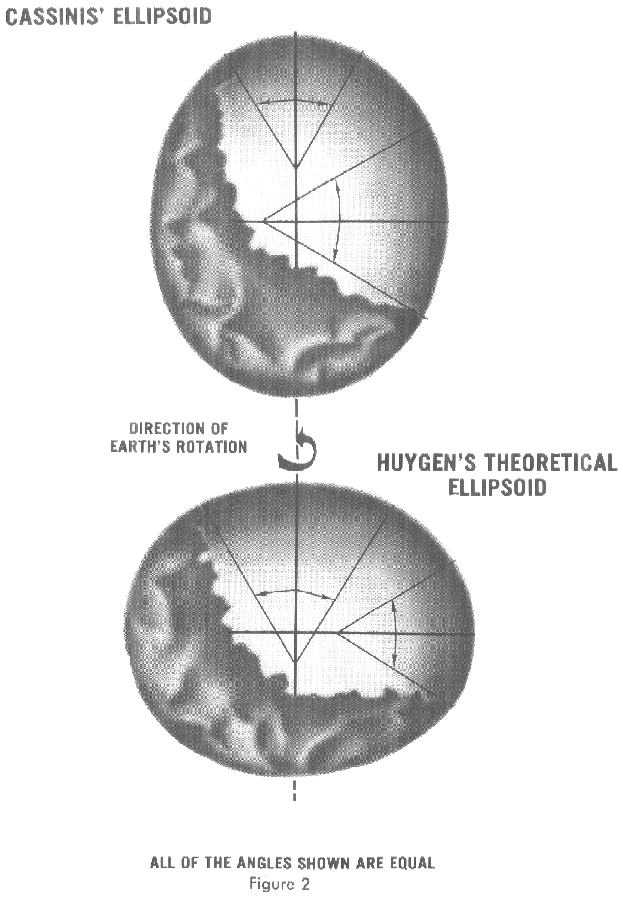This result, if correct, meant that the earth was not a sphere, but an oblong (egg-shaped) ellipsoid—which contradicted the computations by Isaac Newton
and Christiaan Huygens. Newton's theory of gravitation predicted the Earth to be an oblate spheroid with a flattening
of 1:230.
The issue could be settled by measuring, for a number of points on earth, the relationship between their distance (in north-south direction) and the angles between their astronomical verticals (the projection of the vertical direction
on the sky). On an oblate Earth the meridional distance corresponding to one degree would grow toward the poles.
The French Academy of Sciences
dispatched two expeditions – see French Geodesic Mission
. One expedition under Pierre Louis Maupertuis
(1736–37) was sent to Torne Valley
(as far North as possible). The second mission
under Pierre Bouguer
was sent to what is modern-day Ecuador
, near the equator (1735–44).
The measurements conclusively showed that the earth was oblate, with a flattening of 1:210. Thus the next approximation to the true figure of the Earth after the sphere became the oblong ellipsoid of revolution.
Bouguer noticed, as did George Everest
in the 19th century Great Trigonometric Survey
of India, that the astronomical vertical tended to be pulled in the direction of large mountain ranges, due to the gravitation
al attraction of these huge piles of rock. As this vertical is everywhere perpendicular to the idealized surface of mean sea level, or the geoid
, this means that the figure of the Earth is even more irregular than an ellipsoid of revolution. Thus the study of the "undulation of the geoid
" became the next great undertaking in the science of studying the figure of the Earth.
In the late 19th century the Zentralbüro für die Internationale Erdmessung (that is, Central Bureau for International Geodesy) was established by Austria-Hungary
and Germany
. One of its most important goals was the derivation of an international ellipsoid and a gravity formula which should be optimal not only for Europe
but also for the whole world. The Zentralbüro was an early predecessor of the International Association of Geodesy
(IAG) and the International Union of Geodesy and Geophysics
(IUGG) which was founded in 1919.
Most of the relevant theories were derived by the German geodesist Friedrich Robert Helmert
in his famous books Die mathematischen und physikalischen Theorieen der höheren Geodäsie, Einleitung und 1 Teil (1880); English translation: Mathematical and Physical Theories of Higher Geodesy, Vol. 1. Helmert also derived the first global ellipsoid in 1906 with an accuracy of 100 meters (0.002 percent of the Earth's radii). The US
geodesist Hayford
derived a global ellipsoid in ~1910, based on intercontinental isostasy
and an accuracy of 200 m. It was adopted by the IUGG as "international ellipsoid 1924".
Humanity has always been interested in the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
. During very early times this interest was limited, naturally, to the immediate vicinity of home and residency, and the fact that we live on a near spherical globe may or may not have been apparent. As humanity developed, so did its interest in understanding and mapping the size, shape, and composition of the Earth.
Hellenic world
Early ideas about the figure of the Earth held the Earth to be flat (see flat earthFlat Earth
The Flat Earth model is a belief that the Earth's shape is a plane or disk. Most ancient cultures have had conceptions of a flat Earth, including Greece until the classical period, the Bronze Age and Iron Age civilizations of the Near East until the Hellenistic period, India until the Gupta period ...
), and the heavens a physical dome spanning over it. Two early arguments for a spherical earth were that lunar eclipses were seen as circular shadows which could only be caused by a spherical Earth, and that Polaris
Polaris
Polaris |Alpha]] Ursae Minoris, commonly North Star or Pole Star, also Lodestar) is the brightest star in the constellation Ursa Minor. It is very close to the north celestial pole, making it the current northern pole star....
is seen lower in the sky as one travels South.
The early Greeks
Ancient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
, in their speculation and theorizing, ranged from the flat disc advocated by Homer
Homer
In the Western classical tradition Homer , is the author of the Iliad and the Odyssey, and is revered as the greatest ancient Greek epic poet. These epics lie at the beginning of the Western canon of literature, and have had an enormous influence on the history of literature.When he lived is...
to the spherical body postulated by Pythagoras
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
— an idea supported one hundred years later by Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
. Pythagoras was a mathematician and to him the most perfect figure was a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
. He reasoned that the gods would create a perfect figure and therefore the earth was created to be spherical in shape. Anaximenes
Anaximenes of Miletus
Anaximenes of Miletus was an Archaic Greek Pre-Socratic philosopher active in the latter half of the 6th century BC. One of the three Milesian philosophers, he is identified as a younger friend or student of Anaximander. Anaximenes, like others in his school of thought, practiced material monism...
, an early Greek scientist, believed strongly that the earth was rectangular in shape.
Since the spherical shape was the most widely supported during the Greek Era, efforts to determine its size followed. Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
determined the circumference of the earth to be 400,000 stadia (between 62,800 km/39,250 mi and 74,000 km/46,250 mi ) while Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
estimated 300,000 stadia ( 55,500 kilometre
Kilometre
The kilometre is a unit of length in the metric system, equal to one thousand metres and is therefore exactly equal to the distance travelled by light in free space in of a second...
s/34,687 mile
Mile
A mile is a unit of length, most commonly 5,280 feet . The mile of 5,280 feet is sometimes called the statute mile or land mile to distinguish it from the nautical mile...
s ), using the Hellenic stadia which scholars generally take to be 185 meters or 1/10 of a geographical mile
Geographical mile
The geographical mile is a unit of length determined by 1 minute of arc along the Earth's equator. For the 1924 International Spheroid this equalled 1855.4 metres...
. Plato's figure was a guess and Archimedes' a more conservative approximation.
Hellenistic world
In Egypt, a Greek scholar and philosopher, EratosthenesEratosthenes
Eratosthenes of Cyrene was a Greek mathematician, poet, athlete, geographer, astronomer, and music theorist.He was the first person to use the word "geography" and invented the discipline of geography as we understand it...
(276 BC– 195 BC), is said to have made more explicit measurements. He had heard that on the longest day of the summer solstice
Solstice
A solstice is an astronomical event that happens twice each year when the Sun's apparent position in the sky, as viewed from Earth, reaches its northernmost or southernmost extremes...
, the midday sun shone to the bottom of a well in the town of Syene (Aswan
Aswan
Aswan , formerly spelled Assuan, is a city in the south of Egypt, the capital of the Aswan Governorate.It stands on the east bank of the Nile at the first cataract and is a busy market and tourist centre...
). At the same time, he observed the sun was not directly overhead at Alexandria
Alexandria
Alexandria is the second-largest city of Egypt, with a population of 4.1 million, extending about along the coast of the Mediterranean Sea in the north central part of the country; it is also the largest city lying directly on the Mediterranean coast. It is Egypt's largest seaport, serving...
; instead, it cast a shadow with the vertical equal to 1/50th of a circle (7° 12'). To these observations, Eratosthenes applied certain "known" facts (1) that on the day of the summer solstice, the midday sun was directly over the Tropic of Cancer
Tropic of Cancer
The Tropic of Cancer, also referred to as the Northern tropic, is the circle of latitude on the Earth that marks the most northerly position at which the Sun may appear directly overhead at its zenith...
; (2) Syene was on this tropic; (3) Alexandria and Syene lay on a direct north-south line; (4) The sun was a relatively long way away (Astronomical unit
Astronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
). Legend has it that he had someone walk from Alexandria to Syene to measure the distance: that came out to be equal to 5000 stadia or (at the usual Hellenic 185 meters per stadion) about 925 kilometres.
From these observations, measurements, and/or "known" facts, Eratosthenes concluded that, since the angular deviation of the sun from the vertical direction
Vertical direction
In astronomy, geography, geometry and related sciences and contexts, a direction passing by a given point is said to be vertical if it is locally aligned with the gradient of the gravity field, i.e., with the direction of the gravitational force at that point...
at Alexandria was also the angle of the subtended arc (see illustration), the linear distance between Alexandria and Syene was 1/50 of the circumference of the Earth which thus must be 50×5000 = 250,000 stadia or probably 25,000 geographical miles. The circumference of the Earth is 24,902 miles (40,075.16 km). Over the poles it is more precisely 40,008 km or 24,860 statute miles. The actual unit of measure used by Eratosthenes was the stadion. No one knows for sure what his stadion equals in today's units, but most current specialists in antiquities accept that it was the regular Hellenic 185 meter stadion, and few if any would incline to an obscure definition that happened to make Eratosthenes's result correct.
Had the experiment been carried out as described, it would not be remarkable if it agreed with actuality. What is remarkable is that the result was probably about one sixth too high. His measurements were subject to several inaccuracies: (1) though at the summer solstice the noon sun is overhead at the Tropic of Cancer, Syene was not exactly on the tropic (which was at 23° 43' latitude in that day) but about 22 geographical miles to the north; (2) the difference of latitude between Alexandria (31.2 degrees north latitude) and Syene (24.1 degrees) is really 7.1 degrees rather than the perhaps rounded (1/50 of a circle) value of 7° 12' that Eratosthenes used; (4) the actual solstice zenith distance of the noon sun at Alexandria was 31° 12' − 23° 43' = 7° 29' or about 1/48 of a circle not 1/50 = 7° 12', an error closely consistent with use of a vertical gnomon
Gnomon
The gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....
which fixes not the sun's center but the solar upper limb
Limb darkening
Limb darkening refers to the diminishing of intensity in the image of a star as one moves from the center of the image to the edge or "limb" of the image...
16' higher; (5) the most importantly flawed element, whether he measured or adopted it, was the latitudinal distance from Alexandria to Syene (or the true Tropic somewhat further south) which he appears to have overestimated by a factor that relates to most of the error in his resulting circumference of the earth.
A parallel later legendary ancient measurement of the size of the earth was made by another influential Greek scholar, Posidonius
Posidonius
Posidonius "of Apameia" or "of Rhodes" , was a Greek Stoic philosopher, politician, astronomer, geographer, historian and teacher native to Apamea, Syria. He was acclaimed as the greatest polymath of his age...
. He is said to have noted that the star Canopus
Canopus
Canopus |Alpha]] Carinae) is the brightest star in the southern constellation of Carina and Argo Navis, and the second brightest star in the night-time sky, after Sirius. Canopus's visual magnitude is −0.72, and it has an absolute magnitude of −5.53.Canopus is a supergiant of spectral...
was hidden from view in most parts of Greece but that it just grazed the horizon at Rhodes. Posidonius is supposed to have measured the elevation of Canopus at Alexandria and determined that the angle was 1/48th of circle. He assumed the distance from Alexandria to Rhodes to be 5000 stadia, and so he computed the Earth's circumference in stadia as 48 times 5000 = 240,000. Some scholars see these results as luckily semi-accurate due to cancellation of errors. But since the Canopus observations are both mistaken by over a degree, the "experiment" may be not much more than a recycling of Eratosthenes's numbers, while altering 1/50 to the correct 1/48 of a circle. Later either he or a follower appears to have altered the base distance to agree with Eratosthenes's Alexandria-to-Rhodes figure of 3750 stadia since Posidonius's final circumference was 180,000 stadia, which equals 48×3750 stadia. The 180,000 stadia circumference of Posidonius is suspiciously close to that which results from another unlaborious method of measuring the earth, by timing ocean sun-sets from different heights, a method which produces a size of the earth too low by a factor of 5/6, again due to horizontal refraction.
The abovementioned larger and smaller sizes of the earth were those used by Claudius Ptolemy at different times, 252,000 stadia in the Almagest
Almagest
The Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,...
and 180,000 stadia in the later Geographical Directory. His midcareer conversion resulted in the latter work's systematic exaggeration of degree longitudes in the Mediterranean by a factor close to the ratio of the two seriously differing sizes discussed here, which indicates that the conventional size of the earth was what changed, not the stadion.
Ancient India
The great Indian mathematician AryabhataAryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
(AD 476 - 550) was a pioneer of mathematical astronomy. He describes the earth as being spherical and that it rotates on its axis, among other things in his work Āryabhaṭīya
Aryabhatiya
Āryabhaṭīya or Āryabhaṭīyaṃ, a Sanskrit astronomical treatise, is the magnum opus and only extant work of the 5th century Indian mathematician, Āryabhaṭa.- Structure and style:...
. Aryabhatiya is divided into four sections. Gitika, Ganitha (mathematics), Kalakriya (reckoning of time) and Gola (celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
). The discovery that the earth rotates on its own axis from west to east is described in Aryabhatiya ( Gitika 3,6; Kalakriya 5; Gola 9,10;). For example he explained the apparent motion of heavenly bodies is only an illusion (Gola 9), with the following simile;
- Just as a passenger in a boat moving downstream sees the stationary (trees on the river banks) as traversing upstream, so does an observer on earth see the fixed stars as moving towards the west at exactly the same speed (at which the earth moves from west to east.)
Aryabhatiya also estimates the circumference of Earth, accurate to 1% which is remarkable. Aryabhata gives the radius of planets in terms of the Earth-Sun distance as essentially their periods of rotation around the Sun. He also gave the correct explanation of lunar and solar eclipses and that the Moon shines by reflecting sunlight.
Islamic world
The Muslim scholars, who held to the spherical EarthSpherical Earth
The concept of a spherical Earth dates back to ancient Greek philosophy from around the 6th century BC, but remained a matter of philosophical speculation until the 3rd century BC when Hellenistic astronomy established the spherical shape of the earth as a physical given...
theory, used it to calculate the distance and direction from any given point on the earth to Mecca
Mecca
Mecca is a city in the Hijaz and the capital of Makkah province in Saudi Arabia. The city is located inland from Jeddah in a narrow valley at a height of above sea level...
. This determined the Qibla
Qibla
The Qiblah , also transliterated as Qibla, Kiblah or Kibla, is the direction that should be faced when a Muslim prays during salah...
, or Muslim direction of prayer. Muslim mathematicians
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
developed spherical trigonometry
Spherical trigonometry
Spherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...
which was used in these calculations.
Around AD 830 Caliph al-Ma'mun
Al-Ma'mun
Abū Jaʿfar Abdullāh al-Māʾmūn ibn Harūn was an Abbasid caliph who reigned from 813 until his death in 833...
commissioned a group of astronomers to measure the distance from Tadmur (Palmyra
Palmyra
Palmyra was an ancient city in Syria. In the age of antiquity, it was an important city of central Syria, located in an oasis 215 km northeast of Damascus and 180 km southwest of the Euphrates at Deir ez-Zor. It had long been a vital caravan city for travellers crossing the Syrian desert...
) to al-Raqqah
Ar Raqqah
Ar-Raqqah , also spelled Rakka, is a city in north central Syria located on the north bank of the Euphrates, about 160 km east of Aleppo. It is the capital of the Ar-Raqqah Governorate and one of the main cities of the historical Diyār Muḍar, the western part of the Jazīra...
, in modern Syria
Syria
Syria , officially the Syrian Arab Republic , is a country in Western Asia, bordering Lebanon and the Mediterranean Sea to the West, Turkey to the north, Iraq to the east, Jordan to the south, and Israel to the southwest....
. They found the cities to be separated by one degree of latitude and the distance between them to be 66 2/3 miles and thus calculated the Earth's circumference to be 24,000 miles. Another estimate given was 56 2/3 Arabic miles per degree, which corresponds to 111.8 km per degree and a circumference of 40,248 km, very close to the currently modern values of 111.3 km per degree and 40,068 km circumference, respectively.
Muslim astronomers
Islamic astronomy
Islamic astronomy or Arabic astronomy comprises the astronomical developments made in the Islamic world, particularly during the Islamic Golden Age , and mostly written in the Arabic language. These developments mostly took place in the Middle East, Central Asia, Al-Andalus, and North Africa, and...
and geographers were aware of magnetic declination
Magnetic declination
Magnetic declination is the angle between magnetic north and true north. The declination is positive when the magnetic north is east of true north. The term magnetic variation is a synonym, and is more often used in navigation...
by the 15th century, when the Egyptian Muslim astronomer 'Izz al-Din al-Wafa'i (d. 1469/1471) measured it as 7 degrees from Cairo
Cairo
Cairo , is the capital of Egypt and the largest city in the Arab world and Africa, and the 16th largest metropolitan area in the world. Nicknamed "The City of a Thousand Minarets" for its preponderance of Islamic architecture, Cairo has long been a centre of the region's political and cultural life...
.
Biruni
Of the medieval Persian Abu Rayhan Biruni (973-1048) it is said:At the age of 17, Biruni calculated the latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
of Kath, Khwarazm, using the maximum altitude of the Sun. Biruni also solved a complex geodesic equation in order to accurately compute the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
's circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
, which were close to modern values of the Earth's circumference. His estimate of 6,339.9 km for the Earth radius
Earth radius
Because the Earth is not perfectly spherical, no single value serves as its natural radius. Distances from points on the surface to the center range from 6,353 km to 6,384 km...
was only 16.8 km less than the modern value of 6,356.7 km. In contrast to his predecessors who measured the Earth's circumference by sighting the Sun simultaneously from two different locations, Biruni developed a new method of using trigonometric calculations based on the angle between a plain
Plain
In geography, a plain is land with relatively low relief, that is flat or gently rolling. Prairies and steppes are types of plains, and the archetype for a plain is often thought of as a grassland, but plains in their natural state may also be covered in shrublands, woodland and forest, or...
and mountain
Mountain
Image:Himalaya_annotated.jpg|thumb|right|The Himalayan mountain range with Mount Everestrect 58 14 160 49 Chomo Lonzorect 200 28 335 52 Makalurect 378 24 566 45 Mount Everestrect 188 581 920 656 Tibetan Plateaurect 250 406 340 427 Rong River...
top which yielded more accurate measurements of the Earth's circumference and made it possible for it to be measured by a single person from a single location. Abu Rayhan Biruni's method was intended to avoid "walking across hot, dusty deserts" and the idea came to him when he was on top of a tall mountain in India. From the top of the mountain, he sighted the dip angle which, along with the mountain's height (which he calculated beforehand), he applied to the law of sines
Law of sines
In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
formula. This was the earliest known use of dip angle and the earliest practical use of the law of sines. He also made use of algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
to formulate trigonometric equations and used the astrolabe
Astrolabe
An astrolabe is an elaborate inclinometer, historically used by astronomers, navigators, and astrologers. Its many uses include locating and predicting the positions of the Sun, Moon, planets, and stars, determining local time given local latitude and longitude, surveying, triangulation, and to...
to measure angles. His method can be summarized as follows:
He first calculated the height of the mountain by going to two points at sea level with a known distance apart and then measuring the angle between the plain and the top of the mountain for both points. He made both the measurements using an astrolabe. He then used the following trigonometric formula relating the distance (d) between both points with the tangents of their angles (θ) to determine the height (h) of the mountain:
He then stood at the highest point of the mountain, where he measured the dip angle using an astrolabe. He applied the values he obtained for the dip angle and the mountain's height to the following trigonometric formula in order to calculate the Earth's radius:
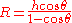
where
- R = Earth radius
- h = height of mountain
- θ = dip angle
Biruni had also, by the age of 22, written a study of map projection
Map projection
A map projection is any method of representing the surface of a sphere or other three-dimensional body on a plane. Map projections are necessary for creating maps. All map projections distort the surface in some fashion...
s, Cartography
Cartography
Cartography is the study and practice of making maps. Combining science, aesthetics, and technique, cartography builds on the premise that reality can be modeled in ways that communicate spatial information effectively.The fundamental problems of traditional cartography are to:*Set the map's...
, which included a method for projecting a hemisphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
on a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
. Around 1025, Biruni was the first to describe a polar equi-azimuthal equidistant projection
Azimuthal equidistant projection
The azimuthal equidistant projection is a type of map projection.A useful application for this type of projection is a polar projection in which all distances measured from the center of the map along any longitudinal line are accurate; an example of a polar azimuthal equidistant projection can be...
of the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
. He was also regarded as the most skilled when it came to mapping cities and measuring the distances between them, which he did for many cities in the Middle East
Middle East
The Middle East is a region that encompasses Western Asia and Northern Africa. It is often used as a synonym for Near East, in opposition to Far East...
and western Indian subcontinent
Indian subcontinent
The Indian subcontinent, also Indian Subcontinent, Indo-Pak Subcontinent or South Asian Subcontinent is a region of the Asian continent on the Indian tectonic plate from the Hindu Kush or Hindu Koh, Himalayas and including the Kuen Lun and Karakoram ranges, forming a land mass which extends...
. He often combined astronomical readings and mathematical equations, in order to develop methods of pin-pointing locations by recording degrees of latitude and longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
. He also developed similar techniques when it came to measuring the heights of mountains, depths of valley
Valley
In geology, a valley or dale is a depression with predominant extent in one direction. A very deep river valley may be called a canyon or gorge.The terms U-shaped and V-shaped are descriptive terms of geography to characterize the form of valleys...
s, and expanse of the horizon, in The Chronology of the Ancient Nations. He also discussed human geography
Human geography
Human geography is one of the two major sub-fields of the discipline of geography. Human geography is the study of the world, its people, communities, and cultures. Human geography differs from physical geography mainly in that it has a greater focus on studying human activities and is more...
and the planetary habitability
Planetary habitability
Planetary habitability is the measure of a planet's or a natural satellite's potential to sustain life. Life may develop directly on a planet or satellite or be transferred to it from another body, a theoretical process known as panspermia...
of the Earth. He hypothesized that roughly a quarter of the Earth's surface is habitable by humans, and also argued that the shores of Asia and Europe were "separated by a vast sea, too dark and dense to navigate and too risky to try".
Medieval Europe
Revising the figures attributed to Posidonius, another Greek philosopher determined 18,000 miles as the Earth's circumference. This last figure was promulgated by PtolemyPtolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
through his world maps. The maps of Ptolemy strongly influenced the cartographers of the Middle Ages
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
. It is probable that Christopher Columbus
Christopher Columbus
Christopher Columbus was an explorer, colonizer, and navigator, born in the Republic of Genoa, in northwestern Italy. Under the auspices of the Catholic Monarchs of Spain, he completed four voyages across the Atlantic Ocean that led to general European awareness of the American continents in the...
, using such maps, was led to believe that Asia was only 3 or 4 thousand miles west of Europe.
Ptolemy's view was not universal, however, and chapter 20 of Mandeville's Travels (c. 1357) supports Erasthenes' calculation.
It was not until the 16th century that his concept of the Earth's size was revised. During that period the Flemish cartographer, Mercator
Gerardus Mercator
thumb|right|200px|Gerardus MercatorGerardus Mercator was a cartographer, born in Rupelmonde in the Hapsburg County of Flanders, part of the Holy Roman Empire. He is remembered for the Mercator projection world map, which is named after him...
, made successive reductions in the size of the Mediterranean Sea
Mediterranean Sea
The Mediterranean Sea is a sea connected to the Atlantic Ocean surrounded by the Mediterranean region and almost completely enclosed by land: on the north by Anatolia and Europe, on the south by North Africa, and on the east by the Levant...
and all of Europe which had the effect of increasing the size of the earth.
Early modern period
The invention of the telescopeTelescope
A telescope is an instrument that aids in the observation of remote objects by collecting electromagnetic radiation . The first known practical telescopes were invented in the Netherlands at the beginning of the 1600s , using glass lenses...
and the theodolite
Theodolite
A theodolite is a precision instrument for measuring angles in the horizontal and vertical planes. Theodolites are mainly used for surveying applications, and have been adapted for specialized purposes in fields like metrology and rocket launch technology...
and the development of logarithm tables allowed exact triangulation
Triangulation
In trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly...
and grade measurement
Grade measurement
Grade measurement is the geodetic determination of the local radius of curvature of the figure of the Earth by determining the difference in astronomical latitude between two locations on the same meridian, the metric distance between which is known....
.
Europe
Jean PicardJean Picard
Jean-Felix Picard was a French astronomer and priest born in La Flèche, where he studied at the Jesuit Collège Royal Henry-Le-Grand. He was the first person to measure the size of the Earth to a reasonable degree of accuracy in a survey conducted in 1669–70, for which he is honored with a...
performed the first modern meridian arc
Meridian arc
In geodesy, a meridian arc measurement is a highly accurate determination of the distance between two points with the same longitude. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This...
measurement in 1699–70. He measured a base line
Baseline (surveying)
In the United States Public Land Survey System, a baseline is the principal east-west line that divides survey townships between north and south. The baseline meets its corresponding meridian at the point of origin, or initial point, for the land survey...
by the aid of wooden rods, used a telescope in his angle measurements, and computed with logarithms. Jacques Cassini
Jacques Cassini
Jacques Cassini was a French astronomer, son of the famous Italian astronomer Giovanni Domenico Cassini.Cassini was born at the Paris Observatory. Admitted at the age of seventeen to membership of the French Academy of Sciences, he was elected in 1696 a fellow of the Royal Society of London, and...
later continued Picard's arc northward to Dunkirk and southward to the Spanish boundary. Cassini divided the measured arc into two parts, one northward from Paris
Paris
Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...
, another southward. When he computed the length of a degree from both chains, he found that the length of one degree in the northern part of the chain was shorter than that in the southern part. See the illustration at right.
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Christiaan Huygens. Newton's theory of gravitation predicted the Earth to be an oblate spheroid with a flattening
Flattening
The flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
of 1:230.
The issue could be settled by measuring, for a number of points on earth, the relationship between their distance (in north-south direction) and the angles between their astronomical verticals (the projection of the vertical direction
Vertical direction
In astronomy, geography, geometry and related sciences and contexts, a direction passing by a given point is said to be vertical if it is locally aligned with the gradient of the gravity field, i.e., with the direction of the gravitational force at that point...
on the sky). On an oblate Earth the meridional distance corresponding to one degree would grow toward the poles.
The French Academy of Sciences
French Academy of Sciences
The French Academy of Sciences is a learned society, founded in 1666 by Louis XIV at the suggestion of Jean-Baptiste Colbert, to encourage and protect the spirit of French scientific research...
dispatched two expeditions – see French Geodesic Mission
French Geodesic Mission
The French Geodesic Mission was an 18th-century expedition to what is now Ecuador carried out for the purpose of measuring the roundness of the Earth and measuring the length of a degree of longitude at the Equator...
. One expedition under Pierre Louis Maupertuis
Pierre Louis Maupertuis
Pierre-Louis Moreau de Maupertuis was a French mathematician, philosopher and man of letters. He became the Director of the Académie des Sciences, and the first President of the Berlin Academy of Science, at the invitation of Frederick the Great....
(1736–37) was sent to Torne Valley
Torne Valley
The Torne Valley or Torne River Valley lies at the border of Sweden and Finland. In 2009 it became one of the Sub-regions of Finland. It is named after the Torne River flowing through the valley and into the Gulf of Bothnia...
(as far North as possible). The second mission
French Geodesic Mission
The French Geodesic Mission was an 18th-century expedition to what is now Ecuador carried out for the purpose of measuring the roundness of the Earth and measuring the length of a degree of longitude at the Equator...
under Pierre Bouguer
Pierre Bouguer
Pierre Bouguer was a French mathematician, geophysicist, geodesist, and astronomer. He is also known as "the father of naval architecture"....
was sent to what is modern-day Ecuador
Ecuador
Ecuador , officially the Republic of Ecuador is a representative democratic republic in South America, bordered by Colombia on the north, Peru on the east and south, and by the Pacific Ocean to the west. It is one of only two countries in South America, along with Chile, that do not have a border...
, near the equator (1735–44).
The measurements conclusively showed that the earth was oblate, with a flattening of 1:210. Thus the next approximation to the true figure of the Earth after the sphere became the oblong ellipsoid of revolution.
Asia and Americas
In South AmericaSouth America
South America is a continent situated in the Western Hemisphere, mostly in the Southern Hemisphere, with a relatively small portion in the Northern Hemisphere. The continent is also considered a subcontinent of the Americas. It is bordered on the west by the Pacific Ocean and on the north and east...
Bouguer noticed, as did George Everest
George Everest
Colonel Sir George Everest was a Welsh surveyor, geographer and Surveyor-General of India from 1830 to 1843.Sir George was largely responsible for completing the section of the Great Trigonometric Survey of India along the meridian arc from the south of India extending north to Nepal, a distance...
in the 19th century Great Trigonometric Survey
Great Trigonometric Survey
The Great Trigonometric Survey was a project of the Survey of India throughout most of the 19th century. It was piloted in its initial stages by William Lambton, and later by George Everest. Among the many accomplishments of the Survey were the demarcation of the British territories in India and...
of India, that the astronomical vertical tended to be pulled in the direction of large mountain ranges, due to the gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
al attraction of these huge piles of rock. As this vertical is everywhere perpendicular to the idealized surface of mean sea level, or the geoid
Geoid
The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
, this means that the figure of the Earth is even more irregular than an ellipsoid of revolution. Thus the study of the "undulation of the geoid
Undulation of the geoid
Undulation of the geoid is the mathematical process of determining the height in meters above the geoid from the height provided by the GPS system which uses the ellipsoid as reference...
" became the next great undertaking in the science of studying the figure of the Earth.
19th century
Austria-Hungary
Austria-Hungary , more formally known as the Kingdoms and Lands Represented in the Imperial Council and the Lands of the Holy Hungarian Crown of Saint Stephen, was a constitutional monarchic union between the crowns of the Austrian Empire and the Kingdom of Hungary in...
and Germany
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
. One of its most important goals was the derivation of an international ellipsoid and a gravity formula which should be optimal not only for Europe
Europe
Europe is, by convention, one of the world's seven continents. Comprising the westernmost peninsula of Eurasia, Europe is generally 'divided' from Asia to its east by the watershed divides of the Ural and Caucasus Mountains, the Ural River, the Caspian and Black Seas, and the waterways connecting...
but also for the whole world. The Zentralbüro was an early predecessor of the International Association of Geodesy
International Association of Geodesy
International Association of Geodesy is an international organization of geodesists, founded in 1940. There are 4 commissions to IAG:*Reference Frames*Gravity Field*Geodynamics and Earth Rotation*Positioning & Applications...
(IAG) and the International Union of Geodesy and Geophysics
International Union of Geodesy and Geophysics
The International Union of Geodesy and Geophysics is a non-governmental organisation dedicated to the scientific study of the Earth using geophysical and geodesic techniques. The IUGG was established in 1919. Some areas within its scope are environmental preservation, reduction of the effects of...
(IUGG) which was founded in 1919.
Most of the relevant theories were derived by the German geodesist Friedrich Robert Helmert
Friedrich Robert Helmert
Friedrich Robert Helmert was a German geodesist and an important writer on the theory of errors.Helmert was born in Freiberg, Kingdom of Saxony. After schooling in Freiberg and Dresden, he entered the Polytechnische Schule, now Technische Universität, in Dresden to study engineering science in 1859...
in his famous books Die mathematischen und physikalischen Theorieen der höheren Geodäsie, Einleitung und 1 Teil (1880); English translation: Mathematical and Physical Theories of Higher Geodesy, Vol. 1. Helmert also derived the first global ellipsoid in 1906 with an accuracy of 100 meters (0.002 percent of the Earth's radii). The US
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
geodesist Hayford
John Fillmore Hayford
- References :...
derived a global ellipsoid in ~1910, based on intercontinental isostasy
Isostasy
Isostasy is a term used in geology to refer to the state of gravitational equilibrium between the earth's lithosphere and asthenosphere such that the tectonic plates "float" at an elevation which depends on their thickness and density. This concept is invoked to explain how different topographic...
and an accuracy of 200 m. It was adopted by the IUGG as "international ellipsoid 1924".