
Lovász number
Encyclopedia
In graph theory
, Lovász number of a graph
is a real number
that is an upper bound
on the Shannon capacity of the graph. It is also known as Lovász theta function and is commonly denoted by ϑ(G). This quantity was first introduced by László Lovász
in his 1979 paper On the Shannon Capacity of a Graph.
on n vertices. An ordered set of n unit vectors U = (ui | i ∈ V) ⊂ RN is called an orthonormal representation of G in RN, if ui and uj are orthogonal whenever vertices i and j are not adjacent in G: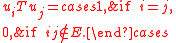
Clearly, every graph admits an orthonormal representation with N = n (just represent vertices by distinct vectors from the standard basis
of Rn), but in general it might be possible to take N considerably smaller than the number of vertices n.
Lovász number ϑ of graph G is defined as follows: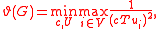
where c is a unit vector in RN and U is an orthonormal representation of G in RN. Here minimization implicitly is performed also over the dimension N, however without loss of generality it suffices to consider N = n. Intuitively, this corresponds to minimizing the half-angle of a rotational cone
containing all representing vectors of an orthonormal representation of G. If the optimal angle is ϕ, then ϑ(G) = 1/cos2(ϕ) and c corresponds to the symmetry axis of the cone.
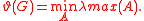
The following method is dual to the previous one. Let B range over all n × n symmetric positive semidefinite matrices such that bij = 0 for every ij ∈ E and Tr(B) = 1. Here Tr denotes trace
(the sum of diagonal entries) and J is the n × n matrix of ones. Then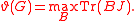
Note that Tr(BJ) is just the sum of all entries of B.
Lovász number can be computed also in terms of the complement graph
. Let d be a unit vector and V = (vi | i ∈ V) be an orthonormal representation of . Then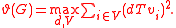
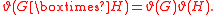
If is the complement
of G, then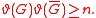
to compute. More precisely,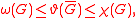
where ω(G) is the clique number of G (the size of the largest clique
) and χ(G) is the chromatic number of G (the smallest number of colors needed to color the vertices of G so that no two adjacent vertices receive the same color). However, the value of ϑ(G) can be approximated by the ellipsoid method
in time bounded by a polynomial in the number of vertices of G.
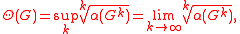
where α(G) is the independence number of graph
G (the size of a largest independent set
of G) and Gk is the strong graph product of G with itself k times. Clearly, Θ(G) ≥ α(G). However, Lovász number provides an upper bound on the Shannon capacity of graph, hence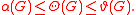
. Since the original paper due it was an open problem to determine the value of Θ(C5). It was first established by that Θ(C5) = .
Clearly, Θ(C5) ≥ α(C5) = 2. However, α(C52) ≥ 5, since "11", "23", "35", "54", "42" are five mutually non-confusable messages, thus Θ(C5) ≥ .
To show that this bound is tight, let U = (u1, ..., u5) be the following orthonormal representation of the pentagon: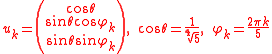
and let c = (1, 0, 0). By using this choice in the initial definition of Lovász number, we get ϑ(C5) ≤ . Hence, Θ(C5) = .

where B is an n × n matrix over some field
, such that bii ≠ 0 and bij = 0 if vertices i and j are not adjacent.
.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, Lovász number of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
that is an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
on the Shannon capacity of the graph. It is also known as Lovász theta function and is commonly denoted by ϑ(G). This quantity was first introduced by László Lovász
László Lovász
László Lovász is a Hungarian mathematician, best known for his work in combinatorics, for which he was awarded the Wolf Prize and the Knuth Prize in 1999, and the Kyoto Prize in 2010....
in his 1979 paper On the Shannon Capacity of a Graph.
Definition
Let G = (V, E) be a graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
on n vertices. An ordered set of n unit vectors U = (ui | i ∈ V) ⊂ RN is called an orthonormal representation of G in RN, if ui and uj are orthogonal whenever vertices i and j are not adjacent in G:
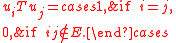
Clearly, every graph admits an orthonormal representation with N = n (just represent vertices by distinct vectors from the standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
of Rn), but in general it might be possible to take N considerably smaller than the number of vertices n.
Lovász number ϑ of graph G is defined as follows:
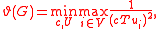
where c is a unit vector in RN and U is an orthonormal representation of G in RN. Here minimization implicitly is performed also over the dimension N, however without loss of generality it suffices to consider N = n. Intuitively, this corresponds to minimizing the half-angle of a rotational cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
containing all representing vectors of an orthonormal representation of G. If the optimal angle is ϕ, then ϑ(G) = 1/cos2(ϕ) and c corresponds to the symmetry axis of the cone.
Equivalent expressions
Let G = (V, E) be a graph on n vertices. Let A range over all n × n symmetric matrices such that aij = 1 whenever i = j or ij ∉ E, and let λmax(A) denote the largest eigenvalue of A. Then an alternative way of computing the Lovász number of G is as follows: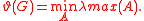
The following method is dual to the previous one. Let B range over all n × n symmetric positive semidefinite matrices such that bij = 0 for every ij ∈ E and Tr(B) = 1. Here Tr denotes trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
(the sum of diagonal entries) and J is the n × n matrix of ones. Then
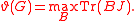
Note that Tr(BJ) is just the sum of all entries of B.
Lovász number can be computed also in terms of the complement graph
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
. Let d be a unit vector and V = (vi | i ∈ V) be an orthonormal representation of . Then
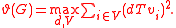
Value of ϑ for some well-known graphs
| Graph | Value of ϑ |
|---|---|
| Complete graph Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... |
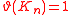 |
| Empty graph | 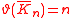 |
| Pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... graph |
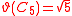 |
| Cycle graph Cycle graph In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn... s |
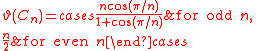 |
| Petersen graph Petersen graph In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it... |
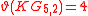 |
| Kneser graph Kneser graph In graph theory, the Kneser graph is the graph whose vertices correspond to the -element subsets of a set of elements, and where two vertices are connected if and only if the two corresponding sets are disjoint... s |
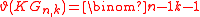 |
| Complete multipartite graphs | 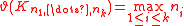 |
Properties
If G ⊠ H denotes the strong graph product of graphs G and H, then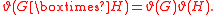
If is the complement
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of G, then
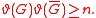
Lovász "sandwich theorem"
The Lovász "sandwich theorem" states that the Lovász number always lies between two other numbers that are NP-completeNP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
to compute. More precisely,
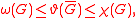
where ω(G) is the clique number of G (the size of the largest clique
Clique
A clique is an exclusive group of people who share common interests, views, purposes, patterns of behavior, or ethnicity. A clique as a reference group can be either normative or comparative. Membership in a clique is typically exclusive, and qualifications for membership may be social or...
) and χ(G) is the chromatic number of G (the smallest number of colors needed to color the vertices of G so that no two adjacent vertices receive the same color). However, the value of ϑ(G) can be approximated by the ellipsoid method
Ellipsoid method
In mathematical optimization, the ellipsoid method is an iterative method for minimizing convex functions. When specialized to solving feasible linear optimization problems with rational data, the ellipsoid method is an algorithm, which finds an optimal solution in a finite number of steps.The...
in time bounded by a polynomial in the number of vertices of G.
Shannon capacity of a graph
Shannon capacity of graph G is defined as follows: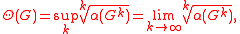
where α(G) is the independence number of graph
Graph
Graph may refer to:* A graphic depicting the relationship between two or more variables used, for instance, in visualising scientific data.In mathematics:* Graph , is a set of vertices and edges....
G (the size of a largest independent set
Independent set (graph theory)
In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
of G) and Gk is the strong graph product of G with itself k times. Clearly, Θ(G) ≥ α(G). However, Lovász number provides an upper bound on the Shannon capacity of graph, hence
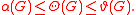
Example (pentagon)
Let the confusability graph of the channel be C5, a pentagonPentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
. Since the original paper due it was an open problem to determine the value of Θ(C5). It was first established by that Θ(C5) = .
Clearly, Θ(C5) ≥ α(C5) = 2. However, α(C52) ≥ 5, since "11", "23", "35", "54", "42" are five mutually non-confusable messages, thus Θ(C5) ≥ .
To show that this bound is tight, let U = (u1, ..., u5) be the following orthonormal representation of the pentagon:
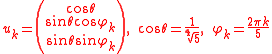
and let c = (1, 0, 0). By using this choice in the initial definition of Lovász number, we get ϑ(C5) ≤ . Hence, Θ(C5) = .
Haemers bound
Haemers has found graphs for which Θ(G) < ϑ(G), i.e., Shannon capacity is strictly smaller than the Lovász number. This means that in general Lovász result is not tight. Haemers has also provided an alternative bound, which is sometimes better than Lovász bound:
where B is an n × n matrix over some field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, such that bii ≠ 0 and bij = 0 if vertices i and j are not adjacent.
Generalizations
Lovász number has been generalized for "non-commutative graphs" in the context of quantum communicationQuantum channel
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
.

