
Möbius transformation
Encyclopedia
In geometry
, a Möbius transformation of the plane is a rational function
of the form

of one complex
variable z; here the coefficients a, b, c, d are complex numbers satisfying ad − bc ≠ 0.
Möbius transformations are named in honor of August Ferdinand Möbius
, although they are also called homographic transformations, linear fractional transformations, or fractional linear transformations.
(i.e. the complex plane
augmented by the point at infinity):
This extended complex plane can be thought of as a sphere, the Riemann sphere
, or as the complex projective line
. Every Möbius transformation is a bijective conformal
map of the Riemann sphere to itself. Indeed, every such map is by necessity a Möbius transformation.
The set of all Möbius transformations forms a group
under composition
called the Möbius group. It is the automorphism group of the Riemann sphere (when considered as a Riemann surface
) and is sometimes denoted .
.
The Möbius group is isomorphic
to the group of orientation-preserving isometries
of hyperbolic 3-space
and therefore plays an important role when studying hyperbolic 3-manifold
s.
In physics
, the identity component
of the Lorentz group
acts on the celestial sphere
in the same way that the Möbius group acts on the Riemann sphere. In fact, these two groups are isomorphic. An observer who accelerates to relativistic velocities will see the pattern of constellations as seen near the Earth continuously transform according to infinitesimal Möbius transformations. This observation is often taken as the starting point of twistor theory
.
Certain subgroup
s of the Möbius group form the automorphism groups of the other simply-connected Riemann surfaces (the complex plane
and the hyperbolic plane
). As such, Möbius transformations play an important role in the theory of Riemann surfaces. The fundamental group
of every Riemann surface is a discrete subgroup of the Möbius group (see Fuchsian group
and Kleinian group
).
A particularly important discrete subgroup of the Möbius group is the modular group
; it is central to the theory of many fractal
s, modular form
s, elliptic curve
s and Pellian equations.
Möbius transformations can be more generally defined in spaces of dimension n>2 as the bijective conformal orientation-preserving maps from the n-sphere to the n-sphere. Such a transformation is the most general form of conformal mapping of a domain. According to Liouville's theorem a Möbius transformation can be expressed as a composition of translations, similarities, orthogonal transformations and inversions.

where a, b, c, d are any complex number
s satisfying ad − bc ≠ 0. (If ad = bc the rational function defined above is a constant and is not considered a Möbius transformation.) In case c≠0 this definition is extended to the whole Riemann sphere
by defining
if c=0 we define
This turns f(z) into a bijective holomorphic function
from the Riemann sphere to the Riemann sphere.
The set of all Möbius transformations forms a group
under composition
. This group can be given the structure of a complex manifold
in such a way that composition and inversion are holomorphic maps. The Möbius group is then a complex Lie group. The Möbius group is usually denoted as it is the automorphism group of the Riemann sphere.
as it is the automorphism group of the Riemann sphere.
then these functions can be composed
, giving

This decomposition makes many properties of the Möbius transformation obvious.
The existence of the inverse Möbius transformation and its explicit formula are easily derived by the composition of the inverse functions of the simpler transformations. That is, define functions such that each
such that each  is the inverse of
is the inverse of  . Then the composition
. Then the composition
gives a formula for the inverse.
Furthermore, Möbius transformations map generalized circles to generalized circles since circle inversion has this property. A generalized circle is either a circle or a line, the latter being considered as a circle through the point at infinity. Note that a Möbius transformation does not necessarily map circles to circles and lines to lines: it can mix the two. Even if it maps a circle to another circle, it does not necessarily map the first circle's center to the second circle's center.
s are invariant under Möbius transformations. That is, if a Möbius transformation maps four distinct points to four distinct points
to four distinct points  respectively, then
respectively, then
If one of the points is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of
is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of  is
is

we can associate the Möbius transformation
The condition ad − bc ≠ 0 is equivalent to the condition that the determinant
of above matrix be nonzero, i.e. that the matrix be invertible.
It is straightforward to check that then the product
of two matrices will be associated with the composition of the two corresponding Möbius transformations.
In other words, the map
from the general linear group
GL(2,C) to the Möbius group,
which sends the matrix to the transformation f, is a group homomorphism
to the transformation f, is a group homomorphism
.
Note that any matrix obtained by multiplying by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up to
by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up to
scalar multiples. In other words: the kernel of π consists of all scalar multiples of the identity matrix
I, and the first isomorphism theorem of group theory states that the quotient group
GL(2,C)/(CI) is isomorphic to the Möbius group. This quotient group is known as the projective linear group
and is usually denoted PGL(2,C).
The same identification of PGL(2,K) with the group of fractional linear transformations and with the group of projective linear automorphisms of the projective line holds over any field K, a fact of algebraic interest, particularly for finite fields, though the case of the complex numbers has the greatest geometric interest.
The natural action
of PGL(2,C) on the complex projective line CP1 is exactly the natural action of the Möbius group on the Riemann sphere, where the projective line CP1 and the Riemann sphere are identified as follows:
Here [z1:z2] are homogeneous coordinates
on CP1; the point [1:0] corresponds to the point ∞ of the Riemann sphere.
By using homogeneous coordinates, many concrete calculations involving Möbius transformations can be simplified, since no case distinctions dealing with ∞ are required.
If one restricts to matrices of determinant one, the map
to matrices of determinant one, the map  restricts to a surjective map from the special linear group
restricts to a surjective map from the special linear group
SL(2,C) to the Möbius group; in the restricted setting the kernel is formed by plus and minus the identity, and the quotient group SL(2,C)/{±I}, denoted by PSL(2,C), is therefore also isomorphic to the Möbius group:
From this we see that the Möbius group is a 3-dimensional complex Lie group (or a 6-dimensional real Lie group). It is a semisimple non-compact
Lie group.
Note that there are precisely two matrices with unit determinant which can be used to represent any given Möbius transformation. That is, SL(2,C) is a double cover of PSL(2,C). Since SL(2,C) is simply-connected it is the universal cover of the Möbius group. Therefore the fundamental group
of the Möbius group is Z2.
of the Möbius group on the Riemann sphere is sharply 3-transitive.) There are several ways to determine f(z) from the given sets of points.

with matrix
maps z1, z2, z3 to 0, 1, ∞, respectively.
(If one of the zi is ∞, then the proper formula for is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)
is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)
If is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix
is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix  which maps
which maps  to
to  becomes
becomes

is equivalent to the equation of a standard hyperbola

in the (z,w)-plane. The problem of constructing a Möbius transformation mapping a triple
mapping a triple  to another triple
to another triple  is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points
is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points  . An explicit equation can be found by evaluating the determinant
. An explicit equation can be found by evaluating the determinant

by means of a Laplace expansion
along the first row. This results in the determinant formulae



for the coefficients of the representing matrix
of the representing matrix  . The constructed matrix
. The constructed matrix  has determinant equal to
has determinant equal to  which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.
which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.
The four types can be distinguished by looking at the trace . Note that the trace is invariant under conjugation
. Note that the trace is invariant under conjugation
, that is,

and so every member of a conjugacy class will have the same trace. Every Möbius transformation can be written such that its representing matrix has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations
has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations  (both not equal to the identity transform) with
(both not equal to the identity transform) with  are conjugate if and only if
are conjugate if and only if 
In the following discussion we will always assume that the representing matrix is normalized such that
is normalized such that  .
.
 of determinant one is said to be parabolic if
of determinant one is said to be parabolic if

(so the trace is plus or minus 2; either can occur for a given transformation since is determined only up to sign). In fact one of the choices for
is determined only up to sign). In fact one of the choices for  has the same characteristic polynomial
has the same characteristic polynomial
X2−2X+1 as the identity matrix, and is therefore unipotent
. A Möbius transform is parabolic if and only if it has exactly one fixed point in the extended complex plane
 , which happens if and only if it can be defined by a matrix conjugate to
, which happens if and only if it can be defined by a matrix conjugate to

which describes a translation in the complex plane.
The set of all parabolic Möbius transformations with a given fixed point in , together with the identity, forms a subgroup
, together with the identity, forms a subgroup
isomorphic to the group of matrices

this is an example of the unipotent radical
of a Borel subgroup
(of the Möbius group, or of SL(2,C) for the matrix group; the notion is defined for any reductive Lie group).

with the complex number not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number
not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number  , called the characteristic constant or multiplier of the transformation.
, called the characteristic constant or multiplier of the transformation.
 whose trace is real
whose trace is real
with

A transform is elliptic if and only if . Writing
. Writing  , an elliptic transform is conjugate to
, an elliptic transform is conjugate to
with real.
real.
Note that for any with characteristic constant k, the characteristic constant of
with characteristic constant k, the characteristic constant of  is
is  . Thus, all Möbius transformations of finite order
. Thus, all Möbius transformations of finite order
are elliptic transformations, namely exactly those where λ is a root of unity
, or, equivalently, where α is a rational
multiple of π
.
 whose trace is real
whose trace is real
with

A transform is hyperbolic if and only if λ is real and positive.
 is not in [0,4]. A transformation is loxodromic if and only if
is not in [0,4]. A transformation is loxodromic if and only if  .
.
Historically, navigation
by loxodrome or rhumb line
refers to a path of constant bearing
; the resulting path is a logarithmic spiral
, similar in shape to the transformations of the complex plane that a loxodromic Möbius transformation makes. See the geometric figures below.
 as the eccentricity
as the eccentricity
of the transformation – division by 2 corrects for the dimension, so the identity has eccentricity 1 (tr/n is sometimes used as an alternative for the trace for this reason), and absolute value corrects for the trace only being defined up to a factor of due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.
due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.
 on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.
on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.

are obtained by solving the fixed point equation . For
. For  , this has two roots obtained by expanding this equation to
, this has two roots obtained by expanding this equation to
and applying the quadratic formula. The roots are
Note that for parabolic transformations, which satisfy , the fixed points coincide. Note also that the discriminant is
, the fixed points coincide. Note also that the discriminant is
When c = 0, the quadratic equation degenerates into a linear equation. This corresponds to the situation that one of the fixed points is the point at infinity. When a ≠ d the second fixed point is finite and is given by

In this case the transformation will be a simple transformation composed of translation
s, rotation
s, and dilations
:

If c = 0 and a = d, then both fixed points are at infinity, and the Möbius transformation corresponds to a pure translation: .
.
of the sphere being 2:
Firstly, the projective linear group
PGL(2,K) is sharply 3-transitive – for any two ordered triples of distinct points, there is a unique map that takes one triple to the other, just as for Möbius transforms, and by the same algebraic proof (essentially dimension counting, as the group is 3-dimensional). Thus any map that fixes at least 3 points is the identity.
Next, the Möbius group is connected, so any map is homotopic to the identity. The Lefschetz–Hopf theorem states that the sum of the indices (in this context, multiplicity) of the fixed points of a map with finitely many fixed points equals the Lefschetz number of the map, which is this case is the trace of the identity map on homology groups, which is simply the Euler characteristic.
By contrast, the projective linear group of the real projective line, PGL(2,R) need not fix any points – for example has no (real) fixed points: as a complex transformation it fixes
has no (real) fixed points: as a complex transformation it fixes  Geometrically this map is the stereographic projection
Geometrically this map is the stereographic projection
of a rotation by 90° around with period 4, which takes
with period 4, which takes  – while the map
– while the map  fixes the two points of 0 and
fixes the two points of 0 and  This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.
This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.
Non-parabolic case:
Every non-parabolic transformation is conjugate
to a dilation/rotation, i.e. a transformation of the form

(k ∈ C) with fixed points at 0 and ∞. To see this define a map

which sends the points to
to  . Here we assume that both
. Here we assume that both  and
and  are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.
are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.
If f has distinct fixed points then the transformation
then the transformation  has fixed points at 0 and ∞ and is therefore a dilation:
has fixed points at 0 and ∞ and is therefore a dilation:  . The fixed point equation for the transformation f can then be written
. The fixed point equation for the transformation f can then be written
Solving for f gives (in matrix form):

or, if one of the fixed points is at infinity:

From the above expressions one can calculate the derivatives of f at the fixed points:
 and
and 
Observe that, given an ordering of the fixed points, we can distinguish one of the multipliers (k) of f as the characteristic constant of f. Reversing the order of the fixed points is equivalent to taking the inverse multiplier for the characteristic constant:
For loxodromic transformations, whenever , one says that
, one says that  is the repulsive fixed point, and
is the repulsive fixed point, and  is the attractive fixed point. For
is the attractive fixed point. For  , the roles are reversed.
, the roles are reversed.
Parabolic case:
In the parabolic case there is only one fixed point . The transformation sending that point to ∞ is
. The transformation sending that point to ∞ is

or the identity if is already at infinity. The transformation
is already at infinity. The transformation  fixes infinity and is therefore a translation:
fixes infinity and is therefore a translation:

Here, β is called the translation length. The fixed point formula for a parabolic transformation is then

Solving for f (in matrix form) gives

or, if :
:

Note that is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:
is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:
The characteristic constant can be expressed in terms of its logarithm
:
When expressed in this way, the real number becomes an expansion factor. It indicates how repulsive the fixed point
becomes an expansion factor. It indicates how repulsive the fixed point  is, and how attractive
is, and how attractive  is.
is.
The real number is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about
is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about  and clockwise about
and clockwise about  .
.
 , then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.
, then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.
If we take the one-parameter subgroup generated by any elliptic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a family of circles which is nested between the two fixed points on the Riemann sphere. In general, the two fixed points can be any two distinct points.
This has an important physical interpretation.
Imagine that some observer rotates with constant angular velocity about some axis. Then we can take the two fixed points to be the North and South poles of the celestial sphere. The appearance of the night sky is now transformed continuously in exactly the manner described by the one-parameter subgroup of elliptic transformations sharing the fixed points , and with the number
, and with the number  corresponding to the constant angular velocity of our observer.
corresponding to the constant angular velocity of our observer.
Here are some figures illustrating the effect of an elliptic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):
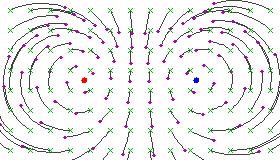
These pictures illustrate the effect of a single Möbius transformation. The one-parameter subgroup which it generates continuously moves points along the family of circular arcs suggested by the pictures.
 If
If  is zero (or a multiple of
is zero (or a multiple of  ), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.
), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.
If we take the one-parameter subgroup
generated by any hyperbolic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of circular arcs away from the first fixed point and toward the second fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
This too has an important physical interpretation. Imagine that an observer accelerates (with constant magnitude of acceleration) in the direction of the North pole on his celestial sphere. Then the appearance of the night sky is transformed in exactly the manner described by the one-parameter subgroup of hyperbolic transformations sharing the fixed points , with the real number
, with the real number  corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).
corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).
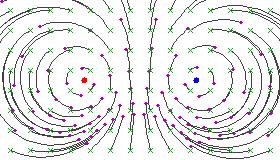
Here are some figures illustrating the effect of a hyperbolic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):
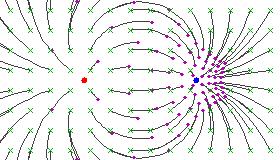
These pictures resemble the field lines of a positive and a negative electrical charge located at the fixed points, because the circular flow lines subtend a constant angle between the two fixed points.
The word "loxodrome" is from the Greek: "λοξος (loxos), slanting + δρόμος (dromos), course". When sailing
on a constant bearing
- if you maintain a heading of (say) north-east, you will eventually wind up sailing around the north pole
in a logarithmic spiral
. On the mercator projection
such a course is a straight line, as the north and south poles project to infinity. The angle that the loxodrome subtends relative to the lines of longitude (i.e. its slope, the "tightness" of the spiral) is the argument of k. Of course, Möbius transformations may have their two fixed points anywhere, not just at the north and south poles. But any loxodromic transformation will be conjugate to a transform that moves all points along such loxodromes.
If we take the one-parameter subgroup
generated by any loxodromic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of curves, away from the first fixed point and toward the second fixed point. Unlike the hyperbolic case, these curves are not circular arcs, but certain curves which under stereographic projection from the sphere to the plane appear as spiral curves which twist counterclockwise infinitely often around one fixed point and twist clockwise infinitely often around the other fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
You can probably guess the physical interpretation in the case when the two fixed points are : an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points
: an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points  , and with
, and with  determined respectively by the magnitude of the actual linear and angular velocities.
determined respectively by the magnitude of the actual linear and angular velocities.
onto the Riemann sphere
. Note in particular that when projected onto a sphere, the special case of a fixed point at infinity looks no different from having the fixed points in an arbitrary location.
 has fixed points
has fixed points  , and characteristic constant k, then
, and characteristic constant k, then  will have
will have  ,
,  ,
,  .
.
This can be used to iterate a transformation, or to animate one by breaking it up into steps.
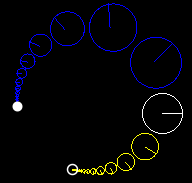
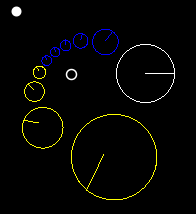
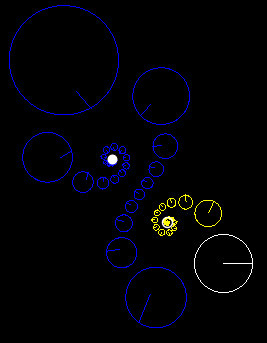
These images show three points (red, blue and black) continuously iterated under transformations with various characteristic constants.
And these images demonstrate what happens when you transform a circle under Hyperbolic, Elliptical, and Loxodromic transforms. Note that in the elliptical and loxodromic images, the α value is 1/10 .
In geometry
, a Möbius transformation of the plane is a rational function
of the form

of one complex
variable z; here the coefficients a, b, c, d are complex numbers satisfying ad − bc ≠ 0.
Möbius transformations are named in honor of August Ferdinand Möbius
, although they are also called homographic transformations, linear fractional transformations, or fractional linear transformations.
(i.e. the complex plane
augmented by the point at infinity):
This extended complex plane can be thought of as a sphere, the Riemann sphere
, or as the complex projective line
. Every Möbius transformation is a bijective conformal
map of the Riemann sphere to itself. Indeed, every such map is by necessity a Möbius transformation.
The set of all Möbius transformations forms a group
under composition
called the Möbius group. It is the automorphism group of the Riemann sphere (when considered as a Riemann surface
) and is sometimes denoted .
.
The Möbius group is isomorphic
to the group of orientation-preserving isometries
of hyperbolic 3-space
and therefore plays an important role when studying hyperbolic 3-manifold
s.
In physics
, the identity component
of the Lorentz group
acts on the celestial sphere
in the same way that the Möbius group acts on the Riemann sphere. In fact, these two groups are isomorphic. An observer who accelerates to relativistic velocities will see the pattern of constellations as seen near the Earth continuously transform according to infinitesimal Möbius transformations. This observation is often taken as the starting point of twistor theory
.
Certain subgroup
s of the Möbius group form the automorphism groups of the other simply-connected Riemann surfaces (the complex plane
and the hyperbolic plane
). As such, Möbius transformations play an important role in the theory of Riemann surfaces. The fundamental group
of every Riemann surface is a discrete subgroup of the Möbius group (see Fuchsian group
and Kleinian group
).
A particularly important discrete subgroup of the Möbius group is the modular group
; it is central to the theory of many fractal
s, modular form
s, elliptic curve
s and Pellian equations.
Möbius transformations can be more generally defined in spaces of dimension n>2 as the bijective conformal orientation-preserving maps from the n-sphere to the n-sphere. Such a transformation is the most general form of conformal mapping of a domain. According to Liouville's theorem a Möbius transformation can be expressed as a composition of translations, similarities, orthogonal transformations and inversions.

where a, b, c, d are any complex number
s satisfying ad − bc ≠ 0. (If ad = bc the rational function defined above is a constant and is not considered a Möbius transformation.) In case c≠0 this definition is extended to the whole Riemann sphere
by defining
if c=0 we define
This turns f(z) into a bijective holomorphic function
from the Riemann sphere to the Riemann sphere.
The set of all Möbius transformations forms a group
under composition
. This group can be given the structure of a complex manifold
in such a way that composition and inversion are holomorphic maps. The Möbius group is then a complex Lie group. The Möbius group is usually denoted as it is the automorphism group of the Riemann sphere.
as it is the automorphism group of the Riemann sphere.
then these functions can be composed
, giving

This decomposition makes many properties of the Möbius transformation obvious.
The existence of the inverse Möbius transformation and its explicit formula are easily derived by the composition of the inverse functions of the simpler transformations. That is, define functions such that each
such that each  is the inverse of
is the inverse of  . Then the composition
. Then the composition
gives a formula for the inverse.
Furthermore, Möbius transformations map generalized circles to generalized circles since circle inversion has this property. A generalized circle is either a circle or a line, the latter being considered as a circle through the point at infinity. Note that a Möbius transformation does not necessarily map circles to circles and lines to lines: it can mix the two. Even if it maps a circle to another circle, it does not necessarily map the first circle's center to the second circle's center.
s are invariant under Möbius transformations. That is, if a Möbius transformation maps four distinct points to four distinct points
to four distinct points  respectively, then
respectively, then
If one of the points is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of
is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of  is
is

we can associate the Möbius transformation
The condition ad − bc ≠ 0 is equivalent to the condition that the determinant
of above matrix be nonzero, i.e. that the matrix be invertible.
It is straightforward to check that then the product
of two matrices will be associated with the composition of the two corresponding Möbius transformations.
In other words, the map
from the general linear group
GL(2,C) to the Möbius group,
which sends the matrix to the transformation f, is a group homomorphism
to the transformation f, is a group homomorphism
.
Note that any matrix obtained by multiplying by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up to
by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up to
scalar multiples. In other words: the kernel of π consists of all scalar multiples of the identity matrix
I, and the first isomorphism theorem of group theory states that the quotient group
GL(2,C)/(CI) is isomorphic to the Möbius group. This quotient group is known as the projective linear group
and is usually denoted PGL(2,C).
The same identification of PGL(2,K) with the group of fractional linear transformations and with the group of projective linear automorphisms of the projective line holds over any field K, a fact of algebraic interest, particularly for finite fields, though the case of the complex numbers has the greatest geometric interest.
The natural action
of PGL(2,C) on the complex projective line CP1 is exactly the natural action of the Möbius group on the Riemann sphere, where the projective line CP1 and the Riemann sphere are identified as follows:
Here [z1:z2] are homogeneous coordinates
on CP1; the point [1:0] corresponds to the point ∞ of the Riemann sphere.
By using homogeneous coordinates, many concrete calculations involving Möbius transformations can be simplified, since no case distinctions dealing with ∞ are required.
If one restricts to matrices of determinant one, the map
to matrices of determinant one, the map  restricts to a surjective map from the special linear group
restricts to a surjective map from the special linear group
SL(2,C) to the Möbius group; in the restricted setting the kernel is formed by plus and minus the identity, and the quotient group SL(2,C)/{±I}, denoted by PSL(2,C), is therefore also isomorphic to the Möbius group:
From this we see that the Möbius group is a 3-dimensional complex Lie group (or a 6-dimensional real Lie group). It is a semisimple non-compact
Lie group.
Note that there are precisely two matrices with unit determinant which can be used to represent any given Möbius transformation. That is, SL(2,C) is a double cover of PSL(2,C). Since SL(2,C) is simply-connected it is the universal cover of the Möbius group. Therefore the fundamental group
of the Möbius group is Z2.
of the Möbius group on the Riemann sphere is sharply 3-transitive.) There are several ways to determine f(z) from the given sets of points.

with matrix
maps z1, z2, z3 to 0, 1, ∞, respectively.
(If one of the zi is ∞, then the proper formula for is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)
is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)
If is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix
is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix  which maps
which maps  to
to  becomes
becomes

is equivalent to the equation of a standard hyperbola

in the (z,w)-plane. The problem of constructing a Möbius transformation mapping a triple
mapping a triple  to another triple
to another triple  is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points
is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points  . An explicit equation can be found by evaluating the determinant
. An explicit equation can be found by evaluating the determinant

by means of a Laplace expansion
along the first row. This results in the determinant formulae



for the coefficients of the representing matrix
of the representing matrix  . The constructed matrix
. The constructed matrix  has determinant equal to
has determinant equal to  which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.
which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.
The four types can be distinguished by looking at the trace . Note that the trace is invariant under conjugation
. Note that the trace is invariant under conjugation
, that is,

and so every member of a conjugacy class will have the same trace. Every Möbius transformation can be written such that its representing matrix has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations
has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations  (both not equal to the identity transform) with
(both not equal to the identity transform) with  are conjugate if and only if
are conjugate if and only if 
In the following discussion we will always assume that the representing matrix is normalized such that
is normalized such that  .
.
 of determinant one is said to be parabolic if
of determinant one is said to be parabolic if

(so the trace is plus or minus 2; either can occur for a given transformation since is determined only up to sign). In fact one of the choices for
is determined only up to sign). In fact one of the choices for  has the same characteristic polynomial
has the same characteristic polynomial
X2−2X+1 as the identity matrix, and is therefore unipotent
. A Möbius transform is parabolic if and only if it has exactly one fixed point in the extended complex plane
 , which happens if and only if it can be defined by a matrix conjugate to
, which happens if and only if it can be defined by a matrix conjugate to

which describes a translation in the complex plane.
The set of all parabolic Möbius transformations with a given fixed point in , together with the identity, forms a subgroup
, together with the identity, forms a subgroup
isomorphic to the group of matrices

this is an example of the unipotent radical
of a Borel subgroup
(of the Möbius group, or of SL(2,C) for the matrix group; the notion is defined for any reductive Lie group).

with the complex number not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number
not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number  , called the characteristic constant or multiplier of the transformation.
, called the characteristic constant or multiplier of the transformation.
 whose trace is real
whose trace is real
with

A transform is elliptic if and only if . Writing
. Writing  , an elliptic transform is conjugate to
, an elliptic transform is conjugate to
with real.
real.
Note that for any with characteristic constant k, the characteristic constant of
with characteristic constant k, the characteristic constant of  is
is  . Thus, all Möbius transformations of finite order
. Thus, all Möbius transformations of finite order
are elliptic transformations, namely exactly those where λ is a root of unity
, or, equivalently, where α is a rational
multiple of π
.
 whose trace is real
whose trace is real
with

A transform is hyperbolic if and only if λ is real and positive.
 is not in [0,4]. A transformation is loxodromic if and only if
is not in [0,4]. A transformation is loxodromic if and only if  .
.
Historically, navigation
by loxodrome or rhumb line
refers to a path of constant bearing
; the resulting path is a logarithmic spiral
, similar in shape to the transformations of the complex plane that a loxodromic Möbius transformation makes. See the geometric figures below.
 as the eccentricity
as the eccentricity
of the transformation – division by 2 corrects for the dimension, so the identity has eccentricity 1 (tr/n is sometimes used as an alternative for the trace for this reason), and absolute value corrects for the trace only being defined up to a factor of due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.
due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.
 on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.
on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.

are obtained by solving the fixed point equation . For
. For  , this has two roots obtained by expanding this equation to
, this has two roots obtained by expanding this equation to
and applying the quadratic formula. The roots are
Note that for parabolic transformations, which satisfy , the fixed points coincide. Note also that the discriminant is
, the fixed points coincide. Note also that the discriminant is
When c = 0, the quadratic equation degenerates into a linear equation. This corresponds to the situation that one of the fixed points is the point at infinity. When a ≠ d the second fixed point is finite and is given by

In this case the transformation will be a simple transformation composed of translation
s, rotation
s, and dilations
:

If c = 0 and a = d, then both fixed points are at infinity, and the Möbius transformation corresponds to a pure translation: .
.
of the sphere being 2:
Firstly, the projective linear group
PGL(2,K) is sharply 3-transitive – for any two ordered triples of distinct points, there is a unique map that takes one triple to the other, just as for Möbius transforms, and by the same algebraic proof (essentially dimension counting, as the group is 3-dimensional). Thus any map that fixes at least 3 points is the identity.
Next, the Möbius group is connected, so any map is homotopic to the identity. The Lefschetz–Hopf theorem states that the sum of the indices (in this context, multiplicity) of the fixed points of a map with finitely many fixed points equals the Lefschetz number of the map, which is this case is the trace of the identity map on homology groups, which is simply the Euler characteristic.
By contrast, the projective linear group of the real projective line, PGL(2,R) need not fix any points – for example has no (real) fixed points: as a complex transformation it fixes
has no (real) fixed points: as a complex transformation it fixes  Geometrically this map is the stereographic projection
Geometrically this map is the stereographic projection
of a rotation by 90° around with period 4, which takes
with period 4, which takes  – while the map
– while the map  fixes the two points of 0 and
fixes the two points of 0 and  This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.
This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.
Non-parabolic case:
Every non-parabolic transformation is conjugate
to a dilation/rotation, i.e. a transformation of the form

(k ∈ C) with fixed points at 0 and ∞. To see this define a map

which sends the points to
to  . Here we assume that both
. Here we assume that both  and
and  are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.
are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.
If f has distinct fixed points then the transformation
then the transformation  has fixed points at 0 and ∞ and is therefore a dilation:
has fixed points at 0 and ∞ and is therefore a dilation:  . The fixed point equation for the transformation f can then be written
. The fixed point equation for the transformation f can then be written
Solving for f gives (in matrix form):

or, if one of the fixed points is at infinity:

From the above expressions one can calculate the derivatives of f at the fixed points:
 and
and 
Observe that, given an ordering of the fixed points, we can distinguish one of the multipliers (k) of f as the characteristic constant of f. Reversing the order of the fixed points is equivalent to taking the inverse multiplier for the characteristic constant:
For loxodromic transformations, whenever , one says that
, one says that  is the repulsive fixed point, and
is the repulsive fixed point, and  is the attractive fixed point. For
is the attractive fixed point. For  , the roles are reversed.
, the roles are reversed.
Parabolic case:
In the parabolic case there is only one fixed point . The transformation sending that point to ∞ is
. The transformation sending that point to ∞ is

or the identity if is already at infinity. The transformation
is already at infinity. The transformation  fixes infinity and is therefore a translation:
fixes infinity and is therefore a translation:

Here, β is called the translation length. The fixed point formula for a parabolic transformation is then

Solving for f (in matrix form) gives

or, if :
:

Note that is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:
is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:

The characteristic constant can be expressed in terms of its logarithm
:
When expressed in this way, the real number becomes an expansion factor. It indicates how repulsive the fixed point
becomes an expansion factor. It indicates how repulsive the fixed point  is, and how attractive
is, and how attractive  is.
is.
The real number is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about
is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about  and clockwise about
and clockwise about  .
.
 , then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.
, then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.
If we take the one-parameter subgroup generated by any elliptic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a family of circles which is nested between the two fixed points on the Riemann sphere. In general, the two fixed points can be any two distinct points.
This has an important physical interpretation.
Imagine that some observer rotates with constant angular velocity about some axis. Then we can take the two fixed points to be the North and South poles of the celestial sphere. The appearance of the night sky is now transformed continuously in exactly the manner described by the one-parameter subgroup of elliptic transformations sharing the fixed points , and with the number
, and with the number  corresponding to the constant angular velocity of our observer.
corresponding to the constant angular velocity of our observer.
Here are some figures illustrating the effect of an elliptic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):


These pictures illustrate the effect of a single Möbius transformation. The one-parameter subgroup which it generates continuously moves points along the family of circular arcs suggested by the pictures.
 If
If  is zero (or a multiple of
is zero (or a multiple of  ), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.
), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.
If we take the one-parameter subgroup
generated by any hyperbolic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of circular arcs away from the first fixed point and toward the second fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
This too has an important physical interpretation. Imagine that an observer accelerates (with constant magnitude of acceleration) in the direction of the North pole on his celestial sphere. Then the appearance of the night sky is transformed in exactly the manner described by the one-parameter subgroup of hyperbolic transformations sharing the fixed points , with the real number
, with the real number  corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).
corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).
Here are some figures illustrating the effect of a hyperbolic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):


These pictures resemble the field lines of a positive and a negative electrical charge located at the fixed points, because the circular flow lines subtend a constant angle between the two fixed points.
The word "loxodrome" is from the Greek: "λοξος (loxos), slanting + δρόμος (dromos), course". When sailing
on a constant bearing
- if you maintain a heading of (say) north-east, you will eventually wind up sailing around the north pole
in a logarithmic spiral
. On the mercator projection
such a course is a straight line, as the north and south poles project to infinity. The angle that the loxodrome subtends relative to the lines of longitude (i.e. its slope, the "tightness" of the spiral) is the argument of k. Of course, Möbius transformations may have their two fixed points anywhere, not just at the north and south poles. But any loxodromic transformation will be conjugate to a transform that moves all points along such loxodromes.
If we take the one-parameter subgroup
generated by any loxodromic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of curves, away from the first fixed point and toward the second fixed point. Unlike the hyperbolic case, these curves are not circular arcs, but certain curves which under stereographic projection from the sphere to the plane appear as spiral curves which twist counterclockwise infinitely often around one fixed point and twist clockwise infinitely often around the other fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
You can probably guess the physical interpretation in the case when the two fixed points are : an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points
: an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points  , and with
, and with  determined respectively by the magnitude of the actual linear and angular velocities.
determined respectively by the magnitude of the actual linear and angular velocities.
onto the Riemann sphere
. Note in particular that when projected onto a sphere, the special case of a fixed point at infinity looks no different from having the fixed points in an arbitrary location.
 has fixed points
has fixed points  , and characteristic constant k, then
, and characteristic constant k, then  will have
will have  ,
,  ,
,  .
.
This can be used to iterate a transformation, or to animate one by breaking it up into steps.
These images show three points (red, blue and black) continuously iterated under transformations with various characteristic constants.
And these images demonstrate what happens when you transform a circle under Hyperbolic, Elliptical, and Loxodromic transforms. Note that in the elliptical and loxodromic images, the α value is 1/10 .



In geometry
, a Möbius transformation of the plane is a rational function
of the form

of one complex
variable z; here the coefficients a, b, c, d are complex numbers satisfying ad − bc ≠ 0.
Möbius transformations are named in honor of August Ferdinand Möbius
, although they are also called homographic transformations, linear fractional transformations, or fractional linear transformations.
(i.e. the complex plane
augmented by the point at infinity):
This extended complex plane can be thought of as a sphere, the Riemann sphere
, or as the complex projective line
. Every Möbius transformation is a bijective conformal
map of the Riemann sphere to itself. Indeed, every such map is by necessity a Möbius transformation.
The set of all Möbius transformations forms a group
under composition
called the Möbius group. It is the automorphism group of the Riemann sphere (when considered as a Riemann surface
) and is sometimes denoted .
.
The Möbius group is isomorphic
to the group of orientation-preserving isometries
of hyperbolic 3-space
and therefore plays an important role when studying hyperbolic 3-manifold
s.
In physics
, the identity component
of the Lorentz group
acts on the celestial sphere
in the same way that the Möbius group acts on the Riemann sphere. In fact, these two groups are isomorphic. An observer who accelerates to relativistic velocities will see the pattern of constellations as seen near the Earth continuously transform according to infinitesimal Möbius transformations. This observation is often taken as the starting point of twistor theory
.
Certain subgroup
s of the Möbius group form the automorphism groups of the other simply-connected Riemann surfaces (the complex plane
and the hyperbolic plane
). As such, Möbius transformations play an important role in the theory of Riemann surfaces. The fundamental group
of every Riemann surface is a discrete subgroup of the Möbius group (see Fuchsian group
and Kleinian group
).
A particularly important discrete subgroup of the Möbius group is the modular group
; it is central to the theory of many fractal
s, modular form
s, elliptic curve
s and Pellian equations.
Möbius transformations can be more generally defined in spaces of dimension n>2 as the bijective conformal orientation-preserving maps from the n-sphere to the n-sphere. Such a transformation is the most general form of conformal mapping of a domain. According to Liouville's theorem a Möbius transformation can be expressed as a composition of translations, similarities, orthogonal transformations and inversions.

where a, b, c, d are any complex number
s satisfying ad − bc ≠ 0. (If ad = bc the rational function defined above is a constant and is not considered a Möbius transformation.) In case c≠0 this definition is extended to the whole Riemann sphere
by defining
if c=0 we define
This turns f(z) into a bijective holomorphic function
from the Riemann sphere to the Riemann sphere.
The set of all Möbius transformations forms a group
under composition
. This group can be given the structure of a complex manifold
in such a way that composition and inversion are holomorphic maps. The Möbius group is then a complex Lie group. The Möbius group is usually denoted as it is the automorphism group of the Riemann sphere.
as it is the automorphism group of the Riemann sphere.
then these functions can be composed
, giving

This decomposition makes many properties of the Möbius transformation obvious.
The existence of the inverse Möbius transformation and its explicit formula are easily derived by the composition of the inverse functions of the simpler transformations. That is, define functions such that each
such that each  is the inverse of
is the inverse of  . Then the composition
. Then the composition
gives a formula for the inverse.
Furthermore, Möbius transformations map generalized circles to generalized circles since circle inversion has this property. A generalized circle is either a circle or a line, the latter being considered as a circle through the point at infinity. Note that a Möbius transformation does not necessarily map circles to circles and lines to lines: it can mix the two. Even if it maps a circle to another circle, it does not necessarily map the first circle's center to the second circle's center.
s are invariant under Möbius transformations. That is, if a Möbius transformation maps four distinct points to four distinct points
to four distinct points  respectively, then
respectively, then
If one of the points is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of
is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of  is
is

we can associate the Möbius transformation
The condition ad − bc ≠ 0 is equivalent to the condition that the determinant
of above matrix be nonzero, i.e. that the matrix be invertible.
It is straightforward to check that then the product
of two matrices will be associated with the composition of the two corresponding Möbius transformations.
In other words, the map
from the general linear group
GL(2,C) to the Möbius group,
which sends the matrix to the transformation f, is a group homomorphism
to the transformation f, is a group homomorphism
.
Note that any matrix obtained by multiplying by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up to
by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up to
scalar multiples. In other words: the kernel of π consists of all scalar multiples of the identity matrix
I, and the first isomorphism theorem of group theory states that the quotient group
GL(2,C)/(CI) is isomorphic to the Möbius group. This quotient group is known as the projective linear group
and is usually denoted PGL(2,C).
The same identification of PGL(2,K) with the group of fractional linear transformations and with the group of projective linear automorphisms of the projective line holds over any field K, a fact of algebraic interest, particularly for finite fields, though the case of the complex numbers has the greatest geometric interest.
The natural action
of PGL(2,C) on the complex projective line CP1 is exactly the natural action of the Möbius group on the Riemann sphere, where the projective line CP1 and the Riemann sphere are identified as follows:
Here [z1:z2] are homogeneous coordinates
on CP1; the point [1:0] corresponds to the point ∞ of the Riemann sphere.
By using homogeneous coordinates, many concrete calculations involving Möbius transformations can be simplified, since no case distinctions dealing with ∞ are required.
If one restricts to matrices of determinant one, the map
to matrices of determinant one, the map  restricts to a surjective map from the special linear group
restricts to a surjective map from the special linear group
SL(2,C) to the Möbius group; in the restricted setting the kernel is formed by plus and minus the identity, and the quotient group SL(2,C)/{±I}, denoted by PSL(2,C), is therefore also isomorphic to the Möbius group:
From this we see that the Möbius group is a 3-dimensional complex Lie group (or a 6-dimensional real Lie group). It is a semisimple non-compact
Lie group.
Note that there are precisely two matrices with unit determinant which can be used to represent any given Möbius transformation. That is, SL(2,C) is a double cover of PSL(2,C). Since SL(2,C) is simply-connected it is the universal cover of the Möbius group. Therefore the fundamental group
of the Möbius group is Z2.
of the Möbius group on the Riemann sphere is sharply 3-transitive.) There are several ways to determine f(z) from the given sets of points.

with matrix
maps z1, z2, z3 to 0, 1, ∞, respectively.
(If one of the zi is ∞, then the proper formula for is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)
is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)
If is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix
is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix  which maps
which maps  to
to  becomes
becomes

is equivalent to the equation of a standard hyperbola

in the (z,w)-plane. The problem of constructing a Möbius transformation mapping a triple
mapping a triple  to another triple
to another triple  is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points
is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points  . An explicit equation can be found by evaluating the determinant
. An explicit equation can be found by evaluating the determinant

by means of a Laplace expansion
along the first row. This results in the determinant formulae



for the coefficients of the representing matrix
of the representing matrix  . The constructed matrix
. The constructed matrix  has determinant equal to
has determinant equal to  which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.
which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.
The four types can be distinguished by looking at the trace . Note that the trace is invariant under conjugation
. Note that the trace is invariant under conjugation
, that is,

and so every member of a conjugacy class will have the same trace. Every Möbius transformation can be written such that its representing matrix has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations
has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations  (both not equal to the identity transform) with
(both not equal to the identity transform) with  are conjugate if and only if
are conjugate if and only if 
In the following discussion we will always assume that the representing matrix is normalized such that
is normalized such that  .
.
 of determinant one is said to be parabolic if
of determinant one is said to be parabolic if

(so the trace is plus or minus 2; either can occur for a given transformation since is determined only up to sign). In fact one of the choices for
is determined only up to sign). In fact one of the choices for  has the same characteristic polynomial
has the same characteristic polynomial
X2−2X+1 as the identity matrix, and is therefore unipotent
. A Möbius transform is parabolic if and only if it has exactly one fixed point in the extended complex plane
 , which happens if and only if it can be defined by a matrix conjugate to
, which happens if and only if it can be defined by a matrix conjugate to

which describes a translation in the complex plane.
The set of all parabolic Möbius transformations with a given fixed point in , together with the identity, forms a subgroup
, together with the identity, forms a subgroup
isomorphic to the group of matrices

this is an example of the unipotent radical
of a Borel subgroup
(of the Möbius group, or of SL(2,C) for the matrix group; the notion is defined for any reductive Lie group).

with the complex number not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number
not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number  , called the characteristic constant or multiplier of the transformation.
, called the characteristic constant or multiplier of the transformation.
 whose trace is real
whose trace is real
with

A transform is elliptic if and only if . Writing
. Writing  , an elliptic transform is conjugate to
, an elliptic transform is conjugate to
with real.
real.
Note that for any with characteristic constant k, the characteristic constant of
with characteristic constant k, the characteristic constant of  is
is  . Thus, all Möbius transformations of finite order
. Thus, all Möbius transformations of finite order
are elliptic transformations, namely exactly those where λ is a root of unity
, or, equivalently, where α is a rational
multiple of π
.
 whose trace is real
whose trace is real
with

A transform is hyperbolic if and only if λ is real and positive.
 is not in [0,4]. A transformation is loxodromic if and only if
is not in [0,4]. A transformation is loxodromic if and only if  .
.
Historically, navigation
by loxodrome or rhumb line
refers to a path of constant bearing
; the resulting path is a logarithmic spiral
, similar in shape to the transformations of the complex plane that a loxodromic Möbius transformation makes. See the geometric figures below.
 as the eccentricity
as the eccentricity
of the transformation – division by 2 corrects for the dimension, so the identity has eccentricity 1 (tr/n is sometimes used as an alternative for the trace for this reason), and absolute value corrects for the trace only being defined up to a factor of due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.
due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.
 on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.
on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.

are obtained by solving the fixed point equation . For
. For  , this has two roots obtained by expanding this equation to
, this has two roots obtained by expanding this equation to
and applying the quadratic formula. The roots are
Note that for parabolic transformations, which satisfy , the fixed points coincide. Note also that the discriminant is
, the fixed points coincide. Note also that the discriminant is
When c = 0, the quadratic equation degenerates into a linear equation. This corresponds to the situation that one of the fixed points is the point at infinity. When a ≠ d the second fixed point is finite and is given by

In this case the transformation will be a simple transformation composed of translation
s, rotation
s, and dilations
:

If c = 0 and a = d, then both fixed points are at infinity, and the Möbius transformation corresponds to a pure translation: .
.
of the sphere being 2:
Firstly, the projective linear group
PGL(2,K) is sharply 3-transitive – for any two ordered triples of distinct points, there is a unique map that takes one triple to the other, just as for Möbius transforms, and by the same algebraic proof (essentially dimension counting, as the group is 3-dimensional). Thus any map that fixes at least 3 points is the identity.
Next, the Möbius group is connected, so any map is homotopic to the identity. The Lefschetz–Hopf theorem states that the sum of the indices (in this context, multiplicity) of the fixed points of a map with finitely many fixed points equals the Lefschetz number of the map, which is this case is the trace of the identity map on homology groups, which is simply the Euler characteristic.
By contrast, the projective linear group of the real projective line, PGL(2,R) need not fix any points – for example has no (real) fixed points: as a complex transformation it fixes
has no (real) fixed points: as a complex transformation it fixes  Geometrically this map is the stereographic projection
Geometrically this map is the stereographic projection
of a rotation by 90° around with period 4, which takes
with period 4, which takes  – while the map
– while the map  fixes the two points of 0 and
fixes the two points of 0 and  This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.
This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.
Non-parabolic case:
Every non-parabolic transformation is conjugate
to a dilation/rotation, i.e. a transformation of the form

(k ∈ C) with fixed points at 0 and ∞. To see this define a map

which sends the points to
to  . Here we assume that both
. Here we assume that both  and
and  are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.
are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.
If f has distinct fixed points then the transformation
then the transformation  has fixed points at 0 and ∞ and is therefore a dilation:
has fixed points at 0 and ∞ and is therefore a dilation:  . The fixed point equation for the transformation f can then be written
. The fixed point equation for the transformation f can then be written
Solving for f gives (in matrix form):

or, if one of the fixed points is at infinity:

From the above expressions one can calculate the derivatives of f at the fixed points:
 and
and 
Observe that, given an ordering of the fixed points, we can distinguish one of the multipliers (k) of f as the characteristic constant of f. Reversing the order of the fixed points is equivalent to taking the inverse multiplier for the characteristic constant:
For loxodromic transformations, whenever , one says that
, one says that  is the repulsive fixed point, and
is the repulsive fixed point, and  is the attractive fixed point. For
is the attractive fixed point. For  , the roles are reversed.
, the roles are reversed.
Parabolic case:
In the parabolic case there is only one fixed point . The transformation sending that point to ∞ is
. The transformation sending that point to ∞ is

or the identity if is already at infinity. The transformation
is already at infinity. The transformation  fixes infinity and is therefore a translation:
fixes infinity and is therefore a translation:

Here, β is called the translation length. The fixed point formula for a parabolic transformation is then

Solving for f (in matrix form) gives

or, if :
:

Note that is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:
is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:

The characteristic constant can be expressed in terms of its logarithm
:
When expressed in this way, the real number becomes an expansion factor. It indicates how repulsive the fixed point
becomes an expansion factor. It indicates how repulsive the fixed point  is, and how attractive
is, and how attractive  is.
is.
The real number is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about
is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about  and clockwise about
and clockwise about  .
.
 , then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.
, then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.
If we take the one-parameter subgroup generated by any elliptic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a family of circles which is nested between the two fixed points on the Riemann sphere. In general, the two fixed points can be any two distinct points.
This has an important physical interpretation.
Imagine that some observer rotates with constant angular velocity about some axis. Then we can take the two fixed points to be the North and South poles of the celestial sphere. The appearance of the night sky is now transformed continuously in exactly the manner described by the one-parameter subgroup of elliptic transformations sharing the fixed points , and with the number
, and with the number  corresponding to the constant angular velocity of our observer.
corresponding to the constant angular velocity of our observer.
Here are some figures illustrating the effect of an elliptic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):


These pictures illustrate the effect of a single Möbius transformation. The one-parameter subgroup which it generates continuously moves points along the family of circular arcs suggested by the pictures.
 If
If  is zero (or a multiple of
is zero (or a multiple of  ), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.
), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.
If we take the one-parameter subgroup
generated by any hyperbolic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of circular arcs away from the first fixed point and toward the second fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
This too has an important physical interpretation. Imagine that an observer accelerates (with constant magnitude of acceleration) in the direction of the North pole on his celestial sphere. Then the appearance of the night sky is transformed in exactly the manner described by the one-parameter subgroup of hyperbolic transformations sharing the fixed points , with the real number
, with the real number  corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).
corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).
Here are some figures illustrating the effect of a hyperbolic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):


These pictures resemble the field lines of a positive and a negative electrical charge located at the fixed points, because the circular flow lines subtend a constant angle between the two fixed points.
The word "loxodrome" is from the Greek: "λοξος (loxos), slanting + δρόμος (dromos), course". When sailing
on a constant bearing
- if you maintain a heading of (say) north-east, you will eventually wind up sailing around the north pole
in a logarithmic spiral
. On the mercator projection
such a course is a straight line, as the north and south poles project to infinity. The angle that the loxodrome subtends relative to the lines of longitude (i.e. its slope, the "tightness" of the spiral) is the argument of k. Of course, Möbius transformations may have their two fixed points anywhere, not just at the north and south poles. But any loxodromic transformation will be conjugate to a transform that moves all points along such loxodromes.
If we take the one-parameter subgroup
generated by any loxodromic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of curves, away from the first fixed point and toward the second fixed point. Unlike the hyperbolic case, these curves are not circular arcs, but certain curves which under stereographic projection from the sphere to the plane appear as spiral curves which twist counterclockwise infinitely often around one fixed point and twist clockwise infinitely often around the other fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
You can probably guess the physical interpretation in the case when the two fixed points are : an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points
: an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points  , and with
, and with  determined respectively by the magnitude of the actual linear and angular velocities.
determined respectively by the magnitude of the actual linear and angular velocities.
onto the Riemann sphere
. Note in particular that when projected onto a sphere, the special case of a fixed point at infinity looks no different from having the fixed points in an arbitrary location.
 has fixed points
has fixed points  , and characteristic constant k, then
, and characteristic constant k, then  will have
will have  ,
,  ,
,  .
.
This can be used to iterate a transformation, or to animate one by breaking it up into steps.
These images show three points (red, blue and black) continuously iterated under transformations with various characteristic constants.
And these images demonstrate what happens when you transform a circle under Hyperbolic, Elliptical, and Loxodromic transforms. Note that in the elliptical and loxodromic images, the α value is 1/10 .




Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Möbius transformation of the plane is a rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
of the form

of one complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
variable z; here the coefficients a, b, c, d are complex numbers satisfying ad − bc ≠ 0.
Möbius transformations are named in honor of August Ferdinand Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
, although they are also called homographic transformations, linear fractional transformations, or fractional linear transformations.
Overview
Möbius transformations are defined on the extended complex planeRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
(i.e. the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
augmented by the point at infinity):

This extended complex plane can be thought of as a sphere, the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, or as the complex projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
. Every Möbius transformation is a bijective conformal
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
map of the Riemann sphere to itself. Indeed, every such map is by necessity a Möbius transformation.
The set of all Möbius transformations forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
called the Möbius group. It is the automorphism group of the Riemann sphere (when considered as a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
) and is sometimes denoted
 .
.The Möbius group is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the group of orientation-preserving isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of hyperbolic 3-space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
and therefore plays an important role when studying hyperbolic 3-manifold
Hyperbolic 3-manifold
A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously...
s.
In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
acts on the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
in the same way that the Möbius group acts on the Riemann sphere. In fact, these two groups are isomorphic. An observer who accelerates to relativistic velocities will see the pattern of constellations as seen near the Earth continuously transform according to infinitesimal Möbius transformations. This observation is often taken as the starting point of twistor theory
Twistor theory
In theoretical and mathematical physics, twistor theory maps the geometric objects of conventional 3+1 space-time into geometric objects in a 4 dimensional space with metric signature...
.
Certain subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of the Möbius group form the automorphism groups of the other simply-connected Riemann surfaces (the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
and the hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
). As such, Möbius transformations play an important role in the theory of Riemann surfaces. The fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of every Riemann surface is a discrete subgroup of the Möbius group (see Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
and Kleinian group
Kleinian group
In mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
).
A particularly important discrete subgroup of the Möbius group is the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
; it is central to the theory of many fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s, modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s, elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s and Pellian equations.
Möbius transformations can be more generally defined in spaces of dimension n>2 as the bijective conformal orientation-preserving maps from the n-sphere to the n-sphere. Such a transformation is the most general form of conformal mapping of a domain. According to Liouville's theorem a Möbius transformation can be expressed as a composition of translations, similarities, orthogonal transformations and inversions.
Definition
The general form of a Möbius transformation is given by
where a, b, c, d are any complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s satisfying ad − bc ≠ 0. (If ad = bc the rational function defined above is a constant and is not considered a Möbius transformation.) In case c≠0 this definition is extended to the whole Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
by defining

if c=0 we define

This turns f(z) into a bijective holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
from the Riemann sphere to the Riemann sphere.
The set of all Möbius transformations forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. This group can be given the structure of a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
in such a way that composition and inversion are holomorphic maps. The Möbius group is then a complex Lie group. The Möbius group is usually denoted
 as it is the automorphism group of the Riemann sphere.
as it is the automorphism group of the Riemann sphere.Decomposition and elementary properties
A Möbius transformation is equivalent to a sequence of simpler transformations. Let:-
 (translationTranslation (geometry)In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
(translationTranslation (geometry)In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
by d/c) -
 (inversionInversion (geometry)In geometry, inversive geometry is the study of those properties of figures that are preserved by a generalization of a type of transformation of the Euclidean plane, called inversion...
(inversionInversion (geometry)In geometry, inversive geometry is the study of those properties of figures that are preserved by a generalization of a type of transformation of the Euclidean plane, called inversion...
and reflectionReflection (mathematics)In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
with respect to the real axis) -
 (dilationDilation (mathematics)In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
(dilationDilation (mathematics)In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
and rotationRotation (mathematics)In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
) -
 (translation by a/c)
(translation by a/c)
then these functions can be composed
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, giving

This decomposition makes many properties of the Möbius transformation obvious.
The existence of the inverse Möbius transformation and its explicit formula are easily derived by the composition of the inverse functions of the simpler transformations. That is, define functions
 such that each
such that each  is the inverse of
is the inverse of  . Then the composition
. Then the composition
gives a formula for the inverse.
Preservation of angles and generalized circles
From this decomposition, we see that Möbius transformations carry over all non-trivial properties of circle inversion. For example, the preservation of angles is reduced to proving that circle inversion preserves angles since the other types of transformations are dilation and isometries (translation, reflection, rotation), which trivially preserve angles.Furthermore, Möbius transformations map generalized circles to generalized circles since circle inversion has this property. A generalized circle is either a circle or a line, the latter being considered as a circle through the point at infinity. Note that a Möbius transformation does not necessarily map circles to circles and lines to lines: it can mix the two. Even if it maps a circle to another circle, it does not necessarily map the first circle's center to the second circle's center.
Cross-ratio preservation
Cross-ratioCross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
s are invariant under Möbius transformations. That is, if a Möbius transformation maps four distinct points
 to four distinct points
to four distinct points  respectively, then
respectively, then
If one of the points
 is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of
is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of  is
is
Projective matrix representations
With every invertible complex 2-by-2 matrix
we can associate the Möbius transformation

The condition ad − bc ≠ 0 is equivalent to the condition that the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of above matrix be nonzero, i.e. that the matrix be invertible.
It is straightforward to check that then the product
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
of two matrices will be associated with the composition of the two corresponding Möbius transformations.
In other words, the map

from the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(2,C) to the Möbius group,
which sends the matrix
 to the transformation f, is a group homomorphism
to the transformation f, is a group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
.
Note that any matrix obtained by multiplying
 by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up to
by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
scalar multiples. In other words: the kernel of π consists of all scalar multiples of the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
I, and the first isomorphism theorem of group theory states that the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
GL(2,C)/(CI) is isomorphic to the Möbius group. This quotient group is known as the projective linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
and is usually denoted PGL(2,C).

The same identification of PGL(2,K) with the group of fractional linear transformations and with the group of projective linear automorphisms of the projective line holds over any field K, a fact of algebraic interest, particularly for finite fields, though the case of the complex numbers has the greatest geometric interest.
The natural action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of PGL(2,C) on the complex projective line CP1 is exactly the natural action of the Möbius group on the Riemann sphere, where the projective line CP1 and the Riemann sphere are identified as follows:

Here [z1:z2] are homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
on CP1; the point [1:0] corresponds to the point ∞ of the Riemann sphere.
By using homogeneous coordinates, many concrete calculations involving Möbius transformations can be simplified, since no case distinctions dealing with ∞ are required.
If one restricts
 to matrices of determinant one, the map
to matrices of determinant one, the map  restricts to a surjective map from the special linear group
restricts to a surjective map from the special linear groupSpecial linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2,C) to the Möbius group; in the restricted setting the kernel is formed by plus and minus the identity, and the quotient group SL(2,C)/{±I}, denoted by PSL(2,C), is therefore also isomorphic to the Möbius group:

From this we see that the Möbius group is a 3-dimensional complex Lie group (or a 6-dimensional real Lie group). It is a semisimple non-compact
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
Lie group.
Note that there are precisely two matrices with unit determinant which can be used to represent any given Möbius transformation. That is, SL(2,C) is a double cover of PSL(2,C). Since SL(2,C) is simply-connected it is the universal cover of the Möbius group. Therefore the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the Möbius group is Z2.
Specifying a transformation by three points
Given a set of three distinct points z1, z2, z3 on the Riemann sphere and a second set of distinct points w1, w2, w3, there exists precisely one Möbius transformation f(z) which maps the zs to the ws, i.e. with f(zi) = wi for i=1,2,3. (In other words: the actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the Möbius group on the Riemann sphere is sharply 3-transitive.) There are several ways to determine f(z) from the given sets of points.
Mapping first to 0, 1, ∞
It is easy to check that the Möbius transformation
with matrix

maps z1, z2, z3 to 0, 1, ∞, respectively.
(If one of the zi is ∞, then the proper formula for
 is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)
is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)If
 is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix
is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix  which maps
which maps  to
to  becomes
becomes
Explicit determinant formula
The equation
is equivalent to the equation of a standard hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...

in the (z,w)-plane. The problem of constructing a Möbius transformation
 mapping a triple
mapping a triple  to another triple
to another triple  is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points
is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points  . An explicit equation can be found by evaluating the determinant
. An explicit equation can be found by evaluating the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

by means of a Laplace expansion
Laplace expansion
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of...
along the first row. This results in the determinant formulae




for the coefficients
 of the representing matrix
of the representing matrix  . The constructed matrix
. The constructed matrix  has determinant equal to
has determinant equal to  which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.
which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.Classification
Non-identity Möbius transformations are commonly classified into four types, parabolic, elliptic, hyperbolic and loxodromic, with the hyperbolic ones being a subclass of the loxodromic ones. The classification has both algebraic and geometric significance. Geometrically, the different types result in different transformations of the complex plane, as the figures below illustrate.The four types can be distinguished by looking at the trace
 . Note that the trace is invariant under conjugation
. Note that the trace is invariant under conjugationConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
, that is,

and so every member of a conjugacy class will have the same trace. Every Möbius transformation can be written such that its representing matrix
 has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations
has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations  (both not equal to the identity transform) with
(both not equal to the identity transform) with  are conjugate if and only if
are conjugate if and only if 
In the following discussion we will always assume that the representing matrix
 is normalized such that
is normalized such that  .
.Parabolic transforms
A non-identity Möbius transformation defined by a matrix of determinant one is said to be parabolic if
of determinant one is said to be parabolic if
(so the trace is plus or minus 2; either can occur for a given transformation since
 is determined only up to sign). In fact one of the choices for
is determined only up to sign). In fact one of the choices for  has the same characteristic polynomial
has the same characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
X2−2X+1 as the identity matrix, and is therefore unipotent
Unipotent
In mathematics, a unipotent element r of a ring R is one such that r − 1 is a nilpotent element, in other words such that some power n is zero....
. A Möbius transform is parabolic if and only if it has exactly one fixed point in the extended complex plane
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
 , which happens if and only if it can be defined by a matrix conjugate to
, which happens if and only if it can be defined by a matrix conjugate toConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...

which describes a translation in the complex plane.
The set of all parabolic Möbius transformations with a given fixed point in
 , together with the identity, forms a subgroup
, together with the identity, forms a subgroupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
isomorphic to the group of matrices

this is an example of the unipotent radical
Unipotent
In mathematics, a unipotent element r of a ring R is one such that r − 1 is a nilpotent element, in other words such that some power n is zero....
of a Borel subgroup
Borel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
(of the Möbius group, or of SL(2,C) for the matrix group; the notion is defined for any reductive Lie group).
Characteristic constant
All non-parabolic transformations have two fixed points and are defined by a matrix conjugate to
with the complex number
 not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number
not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number  , called the characteristic constant or multiplier of the transformation.
, called the characteristic constant or multiplier of the transformation.Elliptic transforms
The transformation is said to be elliptic if it can be represented by a matrix whose trace is real
whose trace is realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
with

A transform is elliptic if and only if
 . Writing
. Writing  , an elliptic transform is conjugate to
, an elliptic transform is conjugate to
with
 real.
real.Note that for any
 with characteristic constant k, the characteristic constant of
with characteristic constant k, the characteristic constant of  is
is  . Thus, all Möbius transformations of finite order
. Thus, all Möbius transformations of finite orderOrder (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
are elliptic transformations, namely exactly those where λ is a root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, or, equivalently, where α is a rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
multiple of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
.
Hyperbolic transforms
The transform is said to be hyperbolic if it can be represented by a matrix whose trace is real
whose trace is realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
with

A transform is hyperbolic if and only if λ is real and positive.
Loxodromic transforms
The transform is said to be loxodromic if is not in [0,4]. A transformation is loxodromic if and only if
is not in [0,4]. A transformation is loxodromic if and only if  .
.Historically, navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
by loxodrome or rhumb line
Rhumb line
In navigation, a rhumb line is a line crossing all meridians of longitude at the same angle, i.e. a path derived from a defined initial bearing...
refers to a path of constant bearing
Bearing (navigation)
In marine navigation, a bearing is the direction one object is from another object, usually, the direction of an object from one's own vessel. In aircraft navigation, a bearing is the actual compass direction of the forward course of the aircraft...
; the resulting path is a logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
, similar in shape to the transformations of the complex plane that a loxodromic Möbius transformation makes. See the geometric figures below.
General classification
| Transformation | Trace squared | Multipliers | Class representative | |
|---|---|---|---|---|
| Elliptic |  |
 |
 |
 |
| Parabolic |  |
 |
 |
 |
| Hyperbolic |  |
  |
 |
 |
| Loxodromic |  |
 |
 |
 |
The real case and a note on terminology
Over the real numbers (if the coefficients must be real), there are no non-hyperbolic loxodromic transformations, and the classification is into elliptic, parabolic, and hyperbolic, as for real conics. The terminology is due to considering half the absolute value of the trace, as the eccentricity
as the eccentricityEccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
of the transformation – division by 2 corrects for the dimension, so the identity has eccentricity 1 (tr/n is sometimes used as an alternative for the trace for this reason), and absolute value corrects for the trace only being defined up to a factor of
 due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.
due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.Fixed points
Every non-identity Möbius transformation has two fixed pointsFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
 on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.
on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.Determining the fixed points
The fixed points of the transformation
are obtained by solving the fixed point equation
 . For
. For  , this has two roots obtained by expanding this equation to
, this has two roots obtained by expanding this equation to
and applying the quadratic formula. The roots are

Note that for parabolic transformations, which satisfy
 , the fixed points coincide. Note also that the discriminant is
, the fixed points coincide. Note also that the discriminant is
When c = 0, the quadratic equation degenerates into a linear equation. This corresponds to the situation that one of the fixed points is the point at infinity. When a ≠ d the second fixed point is finite and is given by

In this case the transformation will be a simple transformation composed of translation
Translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
s, rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s, and dilations
Dilation (mathematics)
In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
:

If c = 0 and a = d, then both fixed points are at infinity, and the Möbius transformation corresponds to a pure translation:
 .
.Topological proof
Topologically, the fact that (non-identity) Möbius transformations fix 2 points corresponds to the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the sphere being 2:

Firstly, the projective linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
PGL(2,K) is sharply 3-transitive – for any two ordered triples of distinct points, there is a unique map that takes one triple to the other, just as for Möbius transforms, and by the same algebraic proof (essentially dimension counting, as the group is 3-dimensional). Thus any map that fixes at least 3 points is the identity.
Next, the Möbius group is connected, so any map is homotopic to the identity. The Lefschetz–Hopf theorem states that the sum of the indices (in this context, multiplicity) of the fixed points of a map with finitely many fixed points equals the Lefschetz number of the map, which is this case is the trace of the identity map on homology groups, which is simply the Euler characteristic.
By contrast, the projective linear group of the real projective line, PGL(2,R) need not fix any points – for example
 has no (real) fixed points: as a complex transformation it fixes
has no (real) fixed points: as a complex transformation it fixes  Geometrically this map is the stereographic projection
Geometrically this map is the stereographic projectionStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
of a rotation by 90° around
 with period 4, which takes
with period 4, which takes  – while the map
– while the map  fixes the two points of 0 and
fixes the two points of 0 and  This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.
This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.Normal form
Möbius transformations are also sometimes written in terms of their fixed points in so-called normal form. We first treat the non-parabolic case, for which there are two distinct fixed points.Non-parabolic case:
Every non-parabolic transformation is conjugate
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
to a dilation/rotation, i.e. a transformation of the form

(k ∈ C) with fixed points at 0 and ∞. To see this define a map

which sends the points
 to
to  . Here we assume that both
. Here we assume that both  and
and  are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.
are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.If f has distinct fixed points
 then the transformation
then the transformation  has fixed points at 0 and ∞ and is therefore a dilation:
has fixed points at 0 and ∞ and is therefore a dilation:  . The fixed point equation for the transformation f can then be written
. The fixed point equation for the transformation f can then be written
Solving for f gives (in matrix form):

or, if one of the fixed points is at infinity:

From the above expressions one can calculate the derivatives of f at the fixed points:
 and
and 
Observe that, given an ordering of the fixed points, we can distinguish one of the multipliers (k) of f as the characteristic constant of f. Reversing the order of the fixed points is equivalent to taking the inverse multiplier for the characteristic constant:

For loxodromic transformations, whenever
 , one says that
, one says that  is the repulsive fixed point, and
is the repulsive fixed point, and  is the attractive fixed point. For
is the attractive fixed point. For  , the roles are reversed.
, the roles are reversed.Parabolic case:
In the parabolic case there is only one fixed point
 . The transformation sending that point to ∞ is
. The transformation sending that point to ∞ is
or the identity if
 is already at infinity. The transformation
is already at infinity. The transformation  fixes infinity and is therefore a translation:
fixes infinity and is therefore a translation:
Here, β is called the translation length. The fixed point formula for a parabolic transformation is then

Solving for f (in matrix form) gives

or, if
 :
:
Note that
 is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:
is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:
Geometric interpretation of the characteristic constant
The following picture depicts (after stereographic transformation from the sphere to the plane) the two fixed points of a Möbius transformation in the non-parabolic case:
The characteristic constant can be expressed in terms of its logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
:

When expressed in this way, the real number
 becomes an expansion factor. It indicates how repulsive the fixed point
becomes an expansion factor. It indicates how repulsive the fixed point  is, and how attractive
is, and how attractive  is.
is.The real number
 is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about
is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about  and clockwise about
and clockwise about  .
.Elliptic transformations
If , then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.
, then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.If we take the one-parameter subgroup generated by any elliptic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a family of circles which is nested between the two fixed points on the Riemann sphere. In general, the two fixed points can be any two distinct points.
This has an important physical interpretation.
Imagine that some observer rotates with constant angular velocity about some axis. Then we can take the two fixed points to be the North and South poles of the celestial sphere. The appearance of the night sky is now transformed continuously in exactly the manner described by the one-parameter subgroup of elliptic transformations sharing the fixed points
 , and with the number
, and with the number  corresponding to the constant angular velocity of our observer.
corresponding to the constant angular velocity of our observer.Here are some figures illustrating the effect of an elliptic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):


These pictures illustrate the effect of a single Möbius transformation. The one-parameter subgroup which it generates continuously moves points along the family of circular arcs suggested by the pictures.
Hyperbolic transformations

 is zero (or a multiple of
is zero (or a multiple of  ), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.
), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.If we take the one-parameter subgroup
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
generated by any hyperbolic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of circular arcs away from the first fixed point and toward the second fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
This too has an important physical interpretation. Imagine that an observer accelerates (with constant magnitude of acceleration) in the direction of the North pole on his celestial sphere. Then the appearance of the night sky is transformed in exactly the manner described by the one-parameter subgroup of hyperbolic transformations sharing the fixed points
 , with the real number
, with the real number  corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).
corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).Here are some figures illustrating the effect of a hyperbolic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):


These pictures resemble the field lines of a positive and a negative electrical charge located at the fixed points, because the circular flow lines subtend a constant angle between the two fixed points.
Loxodromic transformations
If both ρ and α are nonzero, then the transformation is said to be loxodromic. These transformations tend to move all points in S-shaped paths from one fixed point to the other.The word "loxodrome" is from the Greek: "λοξος (loxos), slanting + δρόμος (dromos), course". When sailing
Sailing
Sailing is the propulsion of a vehicle and the control of its movement with large foils called sails. By changing the rigging, rudder, and sometimes the keel or centre board, a sailor manages the force of the wind on the sails in order to move the boat relative to its surrounding medium and...
on a constant bearing
Bearing (navigation)
In marine navigation, a bearing is the direction one object is from another object, usually, the direction of an object from one's own vessel. In aircraft navigation, a bearing is the actual compass direction of the forward course of the aircraft...
- if you maintain a heading of (say) north-east, you will eventually wind up sailing around the north pole
North Pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is, subject to the caveats explained below, defined as the point in the northern hemisphere where the Earth's axis of rotation meets its surface...
in a logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
. On the mercator projection
Mercator projection
The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...
such a course is a straight line, as the north and south poles project to infinity. The angle that the loxodrome subtends relative to the lines of longitude (i.e. its slope, the "tightness" of the spiral) is the argument of k. Of course, Möbius transformations may have their two fixed points anywhere, not just at the north and south poles. But any loxodromic transformation will be conjugate to a transform that moves all points along such loxodromes.
If we take the one-parameter subgroup
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
generated by any loxodromic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of curves, away from the first fixed point and toward the second fixed point. Unlike the hyperbolic case, these curves are not circular arcs, but certain curves which under stereographic projection from the sphere to the plane appear as spiral curves which twist counterclockwise infinitely often around one fixed point and twist clockwise infinitely often around the other fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
You can probably guess the physical interpretation in the case when the two fixed points are
 : an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points
: an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points  , and with
, and with  determined respectively by the magnitude of the actual linear and angular velocities.
determined respectively by the magnitude of the actual linear and angular velocities.Stereographic projection
These images show Möbius transformations stereographically projectedStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
onto the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. Note in particular that when projected onto a sphere, the special case of a fixed point at infinity looks no different from having the fixed points in an arbitrary location.
| One fixed point at infinity | ||
| Fixed points diametrically opposite | ||
| Fixed points in an arbitrary location | ||
Iterating a transformation
If a transformation has fixed points
has fixed points  , and characteristic constant k, then
, and characteristic constant k, then  will have
will have  ,
,  ,
,  .
.This can be used to iterate a transformation, or to animate one by breaking it up into steps.
These images show three points (red, blue and black) continuously iterated under transformations with various characteristic constants.
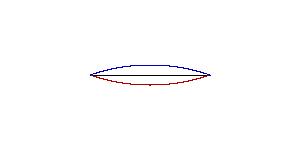 |
 |
 |
|
And these images demonstrate what happens when you transform a circle under Hyperbolic, Elliptical, and Loxodromic transforms. Note that in the elliptical and loxodromic images, the α value is 1/10 .



In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Möbius transformation of the plane is a rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
of the form

of one complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
variable z; here the coefficients a, b, c, d are complex numbers satisfying ad − bc ≠ 0.
Möbius transformations are named in honor of August Ferdinand Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
, although they are also called homographic transformations, linear fractional transformations, or fractional linear transformations.
Overview
Möbius transformations are defined on the extended complex planeRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
(i.e. the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
augmented by the point at infinity):

This extended complex plane can be thought of as a sphere, the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, or as the complex projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
. Every Möbius transformation is a bijective conformal
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
map of the Riemann sphere to itself. Indeed, every such map is by necessity a Möbius transformation.
The set of all Möbius transformations forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
called the Möbius group. It is the automorphism group of the Riemann sphere (when considered as a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
) and is sometimes denoted
 .
.The Möbius group is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the group of orientation-preserving isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of hyperbolic 3-space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
and therefore plays an important role when studying hyperbolic 3-manifold
Hyperbolic 3-manifold
A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously...
s.
In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
acts on the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
in the same way that the Möbius group acts on the Riemann sphere. In fact, these two groups are isomorphic. An observer who accelerates to relativistic velocities will see the pattern of constellations as seen near the Earth continuously transform according to infinitesimal Möbius transformations. This observation is often taken as the starting point of twistor theory
Twistor theory
In theoretical and mathematical physics, twistor theory maps the geometric objects of conventional 3+1 space-time into geometric objects in a 4 dimensional space with metric signature...
.
Certain subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of the Möbius group form the automorphism groups of the other simply-connected Riemann surfaces (the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
and the hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
). As such, Möbius transformations play an important role in the theory of Riemann surfaces. The fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of every Riemann surface is a discrete subgroup of the Möbius group (see Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
and Kleinian group
Kleinian group
In mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
).
A particularly important discrete subgroup of the Möbius group is the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
; it is central to the theory of many fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s, modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s, elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s and Pellian equations.
Möbius transformations can be more generally defined in spaces of dimension n>2 as the bijective conformal orientation-preserving maps from the n-sphere to the n-sphere. Such a transformation is the most general form of conformal mapping of a domain. According to Liouville's theorem a Möbius transformation can be expressed as a composition of translations, similarities, orthogonal transformations and inversions.
Definition
The general form of a Möbius transformation is given by
where a, b, c, d are any complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s satisfying ad − bc ≠ 0. (If ad = bc the rational function defined above is a constant and is not considered a Möbius transformation.) In case c≠0 this definition is extended to the whole Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
by defining

if c=0 we define

This turns f(z) into a bijective holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
from the Riemann sphere to the Riemann sphere.
The set of all Möbius transformations forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. This group can be given the structure of a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
in such a way that composition and inversion are holomorphic maps. The Möbius group is then a complex Lie group. The Möbius group is usually denoted
 as it is the automorphism group of the Riemann sphere.
as it is the automorphism group of the Riemann sphere.Decomposition and elementary properties
A Möbius transformation is equivalent to a sequence of simpler transformations. Let:-
 (translationTranslation (geometry)In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
(translationTranslation (geometry)In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
by d/c) -
 (inversionInversion (geometry)In geometry, inversive geometry is the study of those properties of figures that are preserved by a generalization of a type of transformation of the Euclidean plane, called inversion...
(inversionInversion (geometry)In geometry, inversive geometry is the study of those properties of figures that are preserved by a generalization of a type of transformation of the Euclidean plane, called inversion...
and reflectionReflection (mathematics)In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
with respect to the real axis) -
 (dilationDilation (mathematics)In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
(dilationDilation (mathematics)In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
and rotationRotation (mathematics)In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
) -
 (translation by a/c)
(translation by a/c)
then these functions can be composed
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, giving

This decomposition makes many properties of the Möbius transformation obvious.
The existence of the inverse Möbius transformation and its explicit formula are easily derived by the composition of the inverse functions of the simpler transformations. That is, define functions
 such that each
such that each  is the inverse of
is the inverse of  . Then the composition
. Then the composition
gives a formula for the inverse.
Preservation of angles and generalized circles
From this decomposition, we see that Möbius transformations carry over all non-trivial properties of circle inversion. For example, the preservation of angles is reduced to proving that circle inversion preserves angles since the other types of transformations are dilation and isometries (translation, reflection, rotation), which trivially preserve angles.Furthermore, Möbius transformations map generalized circles to generalized circles since circle inversion has this property. A generalized circle is either a circle or a line, the latter being considered as a circle through the point at infinity. Note that a Möbius transformation does not necessarily map circles to circles and lines to lines: it can mix the two. Even if it maps a circle to another circle, it does not necessarily map the first circle's center to the second circle's center.
Cross-ratio preservation
Cross-ratioCross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
s are invariant under Möbius transformations. That is, if a Möbius transformation maps four distinct points
 to four distinct points
to four distinct points  respectively, then
respectively, then
If one of the points
 is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of
is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of  is
is
Projective matrix representations
With every invertible complex 2-by-2 matrix
we can associate the Möbius transformation

The condition ad − bc ≠ 0 is equivalent to the condition that the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of above matrix be nonzero, i.e. that the matrix be invertible.
It is straightforward to check that then the product
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
of two matrices will be associated with the composition of the two corresponding Möbius transformations.
In other words, the map

from the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(2,C) to the Möbius group,
which sends the matrix
 to the transformation f, is a group homomorphism
to the transformation f, is a group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
.
Note that any matrix obtained by multiplying
 by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up to
by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
scalar multiples. In other words: the kernel of π consists of all scalar multiples of the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
I, and the first isomorphism theorem of group theory states that the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
GL(2,C)/(CI) is isomorphic to the Möbius group. This quotient group is known as the projective linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
and is usually denoted PGL(2,C).

The same identification of PGL(2,K) with the group of fractional linear transformations and with the group of projective linear automorphisms of the projective line holds over any field K, a fact of algebraic interest, particularly for finite fields, though the case of the complex numbers has the greatest geometric interest.
The natural action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of PGL(2,C) on the complex projective line CP1 is exactly the natural action of the Möbius group on the Riemann sphere, where the projective line CP1 and the Riemann sphere are identified as follows:

Here [z1:z2] are homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
on CP1; the point [1:0] corresponds to the point ∞ of the Riemann sphere.
By using homogeneous coordinates, many concrete calculations involving Möbius transformations can be simplified, since no case distinctions dealing with ∞ are required.
If one restricts
 to matrices of determinant one, the map
to matrices of determinant one, the map  restricts to a surjective map from the special linear group
restricts to a surjective map from the special linear groupSpecial linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2,C) to the Möbius group; in the restricted setting the kernel is formed by plus and minus the identity, and the quotient group SL(2,C)/{±I}, denoted by PSL(2,C), is therefore also isomorphic to the Möbius group:

From this we see that the Möbius group is a 3-dimensional complex Lie group (or a 6-dimensional real Lie group). It is a semisimple non-compact
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
Lie group.
Note that there are precisely two matrices with unit determinant which can be used to represent any given Möbius transformation. That is, SL(2,C) is a double cover of PSL(2,C). Since SL(2,C) is simply-connected it is the universal cover of the Möbius group. Therefore the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the Möbius group is Z2.
Specifying a transformation by three points
Given a set of three distinct points z1, z2, z3 on the Riemann sphere and a second set of distinct points w1, w2, w3, there exists precisely one Möbius transformation f(z) which maps the zs to the ws, i.e. with f(zi) = wi for i=1,2,3. (In other words: the actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the Möbius group on the Riemann sphere is sharply 3-transitive.) There are several ways to determine f(z) from the given sets of points.
Mapping first to 0, 1, ∞
It is easy to check that the Möbius transformation
with matrix

maps z1, z2, z3 to 0, 1, ∞, respectively.
(If one of the zi is ∞, then the proper formula for
 is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)
is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)If
 is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix
is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix  which maps
which maps  to
to  becomes
becomes
Explicit determinant formula
The equation
is equivalent to the equation of a standard hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...

in the (z,w)-plane. The problem of constructing a Möbius transformation
 mapping a triple
mapping a triple  to another triple
to another triple  is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points
is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points  . An explicit equation can be found by evaluating the determinant
. An explicit equation can be found by evaluating the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

by means of a Laplace expansion
Laplace expansion
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of...
along the first row. This results in the determinant formulae




for the coefficients
 of the representing matrix
of the representing matrix  . The constructed matrix
. The constructed matrix  has determinant equal to
has determinant equal to  which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.
which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.Classification
Non-identity Möbius transformations are commonly classified into four types, parabolic, elliptic, hyperbolic and loxodromic, with the hyperbolic ones being a subclass of the loxodromic ones. The classification has both algebraic and geometric significance. Geometrically, the different types result in different transformations of the complex plane, as the figures below illustrate.The four types can be distinguished by looking at the trace
 . Note that the trace is invariant under conjugation
. Note that the trace is invariant under conjugationConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
, that is,

and so every member of a conjugacy class will have the same trace. Every Möbius transformation can be written such that its representing matrix
 has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations
has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations  (both not equal to the identity transform) with
(both not equal to the identity transform) with  are conjugate if and only if
are conjugate if and only if 
In the following discussion we will always assume that the representing matrix
 is normalized such that
is normalized such that  .
.Parabolic transforms
A non-identity Möbius transformation defined by a matrix of determinant one is said to be parabolic if
of determinant one is said to be parabolic if
(so the trace is plus or minus 2; either can occur for a given transformation since
 is determined only up to sign). In fact one of the choices for
is determined only up to sign). In fact one of the choices for  has the same characteristic polynomial
has the same characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
X2−2X+1 as the identity matrix, and is therefore unipotent
Unipotent
In mathematics, a unipotent element r of a ring R is one such that r − 1 is a nilpotent element, in other words such that some power n is zero....
. A Möbius transform is parabolic if and only if it has exactly one fixed point in the extended complex plane
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
 , which happens if and only if it can be defined by a matrix conjugate to
, which happens if and only if it can be defined by a matrix conjugate toConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...

which describes a translation in the complex plane.
The set of all parabolic Möbius transformations with a given fixed point in
 , together with the identity, forms a subgroup
, together with the identity, forms a subgroupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
isomorphic to the group of matrices

this is an example of the unipotent radical
Unipotent
In mathematics, a unipotent element r of a ring R is one such that r − 1 is a nilpotent element, in other words such that some power n is zero....
of a Borel subgroup
Borel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
(of the Möbius group, or of SL(2,C) for the matrix group; the notion is defined for any reductive Lie group).
Characteristic constant
All non-parabolic transformations have two fixed points and are defined by a matrix conjugate to
with the complex number
 not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number
not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number  , called the characteristic constant or multiplier of the transformation.
, called the characteristic constant or multiplier of the transformation.Elliptic transforms
The transformation is said to be elliptic if it can be represented by a matrix whose trace is real
whose trace is realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
with

A transform is elliptic if and only if
 . Writing
. Writing  , an elliptic transform is conjugate to
, an elliptic transform is conjugate to
with
 real.
real.Note that for any
 with characteristic constant k, the characteristic constant of
with characteristic constant k, the characteristic constant of  is
is  . Thus, all Möbius transformations of finite order
. Thus, all Möbius transformations of finite orderOrder (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
are elliptic transformations, namely exactly those where λ is a root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, or, equivalently, where α is a rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
multiple of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
.
Hyperbolic transforms
The transform is said to be hyperbolic if it can be represented by a matrix whose trace is real
whose trace is realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
with

A transform is hyperbolic if and only if λ is real and positive.
Loxodromic transforms
The transform is said to be loxodromic if is not in [0,4]. A transformation is loxodromic if and only if
is not in [0,4]. A transformation is loxodromic if and only if  .
.Historically, navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
by loxodrome or rhumb line
Rhumb line
In navigation, a rhumb line is a line crossing all meridians of longitude at the same angle, i.e. a path derived from a defined initial bearing...
refers to a path of constant bearing
Bearing (navigation)
In marine navigation, a bearing is the direction one object is from another object, usually, the direction of an object from one's own vessel. In aircraft navigation, a bearing is the actual compass direction of the forward course of the aircraft...
; the resulting path is a logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
, similar in shape to the transformations of the complex plane that a loxodromic Möbius transformation makes. See the geometric figures below.
General classification
| Transformation | Trace squared | Multipliers | Class representative | |
|---|---|---|---|---|
| Elliptic |  |
 |
 |
 |
| Parabolic |  |
 |
 |
 |
| Hyperbolic |  |
  |
 |
 |
| Loxodromic |  |
 |
 |
 |
The real case and a note on terminology
Over the real numbers (if the coefficients must be real), there are no non-hyperbolic loxodromic transformations, and the classification is into elliptic, parabolic, and hyperbolic, as for real conics. The terminology is due to considering half the absolute value of the trace, as the eccentricity
as the eccentricityEccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
of the transformation – division by 2 corrects for the dimension, so the identity has eccentricity 1 (tr/n is sometimes used as an alternative for the trace for this reason), and absolute value corrects for the trace only being defined up to a factor of
 due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.
due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.Fixed points
Every non-identity Möbius transformation has two fixed pointsFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
 on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.
on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.Determining the fixed points
The fixed points of the transformation
are obtained by solving the fixed point equation
 . For
. For  , this has two roots obtained by expanding this equation to
, this has two roots obtained by expanding this equation to
and applying the quadratic formula. The roots are

Note that for parabolic transformations, which satisfy
 , the fixed points coincide. Note also that the discriminant is
, the fixed points coincide. Note also that the discriminant is
When c = 0, the quadratic equation degenerates into a linear equation. This corresponds to the situation that one of the fixed points is the point at infinity. When a ≠ d the second fixed point is finite and is given by

In this case the transformation will be a simple transformation composed of translation
Translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
s, rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s, and dilations
Dilation (mathematics)
In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
:

If c = 0 and a = d, then both fixed points are at infinity, and the Möbius transformation corresponds to a pure translation:
 .
.Topological proof
Topologically, the fact that (non-identity) Möbius transformations fix 2 points corresponds to the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the sphere being 2:

Firstly, the projective linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
PGL(2,K) is sharply 3-transitive – for any two ordered triples of distinct points, there is a unique map that takes one triple to the other, just as for Möbius transforms, and by the same algebraic proof (essentially dimension counting, as the group is 3-dimensional). Thus any map that fixes at least 3 points is the identity.
Next, the Möbius group is connected, so any map is homotopic to the identity. The Lefschetz–Hopf theorem states that the sum of the indices (in this context, multiplicity) of the fixed points of a map with finitely many fixed points equals the Lefschetz number of the map, which is this case is the trace of the identity map on homology groups, which is simply the Euler characteristic.
By contrast, the projective linear group of the real projective line, PGL(2,R) need not fix any points – for example
 has no (real) fixed points: as a complex transformation it fixes
has no (real) fixed points: as a complex transformation it fixes  Geometrically this map is the stereographic projection
Geometrically this map is the stereographic projectionStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
of a rotation by 90° around
 with period 4, which takes
with period 4, which takes  – while the map
– while the map  fixes the two points of 0 and
fixes the two points of 0 and  This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.
This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.Normal form
Möbius transformations are also sometimes written in terms of their fixed points in so-called normal form. We first treat the non-parabolic case, for which there are two distinct fixed points.Non-parabolic case:
Every non-parabolic transformation is conjugate
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
to a dilation/rotation, i.e. a transformation of the form

(k ∈ C) with fixed points at 0 and ∞. To see this define a map

which sends the points
 to
to  . Here we assume that both
. Here we assume that both  and
and  are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.
are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.If f has distinct fixed points
 then the transformation
then the transformation  has fixed points at 0 and ∞ and is therefore a dilation:
has fixed points at 0 and ∞ and is therefore a dilation:  . The fixed point equation for the transformation f can then be written
. The fixed point equation for the transformation f can then be written
Solving for f gives (in matrix form):

or, if one of the fixed points is at infinity:

From the above expressions one can calculate the derivatives of f at the fixed points:
 and
and 
Observe that, given an ordering of the fixed points, we can distinguish one of the multipliers (k) of f as the characteristic constant of f. Reversing the order of the fixed points is equivalent to taking the inverse multiplier for the characteristic constant:

For loxodromic transformations, whenever
 , one says that
, one says that  is the repulsive fixed point, and
is the repulsive fixed point, and  is the attractive fixed point. For
is the attractive fixed point. For  , the roles are reversed.
, the roles are reversed.Parabolic case:
In the parabolic case there is only one fixed point
 . The transformation sending that point to ∞ is
. The transformation sending that point to ∞ is
or the identity if
 is already at infinity. The transformation
is already at infinity. The transformation  fixes infinity and is therefore a translation:
fixes infinity and is therefore a translation:
Here, β is called the translation length. The fixed point formula for a parabolic transformation is then

Solving for f (in matrix form) gives

or, if
 :
:
Note that
 is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:
is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:
Geometric interpretation of the characteristic constant
The following picture depicts (after stereographic transformation from the sphere to the plane) the two fixed points of a Möbius transformation in the non-parabolic case:
The characteristic constant can be expressed in terms of its logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
:

When expressed in this way, the real number
 becomes an expansion factor. It indicates how repulsive the fixed point
becomes an expansion factor. It indicates how repulsive the fixed point  is, and how attractive
is, and how attractive  is.
is.The real number
 is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about
is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about  and clockwise about
and clockwise about  .
.Elliptic transformations
If , then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.
, then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.If we take the one-parameter subgroup generated by any elliptic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a family of circles which is nested between the two fixed points on the Riemann sphere. In general, the two fixed points can be any two distinct points.
This has an important physical interpretation.
Imagine that some observer rotates with constant angular velocity about some axis. Then we can take the two fixed points to be the North and South poles of the celestial sphere. The appearance of the night sky is now transformed continuously in exactly the manner described by the one-parameter subgroup of elliptic transformations sharing the fixed points
 , and with the number
, and with the number  corresponding to the constant angular velocity of our observer.
corresponding to the constant angular velocity of our observer.Here are some figures illustrating the effect of an elliptic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):


These pictures illustrate the effect of a single Möbius transformation. The one-parameter subgroup which it generates continuously moves points along the family of circular arcs suggested by the pictures.
Hyperbolic transformations

 is zero (or a multiple of
is zero (or a multiple of  ), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.
), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.If we take the one-parameter subgroup
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
generated by any hyperbolic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of circular arcs away from the first fixed point and toward the second fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
This too has an important physical interpretation. Imagine that an observer accelerates (with constant magnitude of acceleration) in the direction of the North pole on his celestial sphere. Then the appearance of the night sky is transformed in exactly the manner described by the one-parameter subgroup of hyperbolic transformations sharing the fixed points
 , with the real number
, with the real number  corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).
corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).Here are some figures illustrating the effect of a hyperbolic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):


These pictures resemble the field lines of a positive and a negative electrical charge located at the fixed points, because the circular flow lines subtend a constant angle between the two fixed points.
Loxodromic transformations
If both ρ and α are nonzero, then the transformation is said to be loxodromic. These transformations tend to move all points in S-shaped paths from one fixed point to the other.The word "loxodrome" is from the Greek: "λοξος (loxos), slanting + δρόμος (dromos), course". When sailing
Sailing
Sailing is the propulsion of a vehicle and the control of its movement with large foils called sails. By changing the rigging, rudder, and sometimes the keel or centre board, a sailor manages the force of the wind on the sails in order to move the boat relative to its surrounding medium and...
on a constant bearing
Bearing (navigation)
In marine navigation, a bearing is the direction one object is from another object, usually, the direction of an object from one's own vessel. In aircraft navigation, a bearing is the actual compass direction of the forward course of the aircraft...
- if you maintain a heading of (say) north-east, you will eventually wind up sailing around the north pole
North Pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is, subject to the caveats explained below, defined as the point in the northern hemisphere where the Earth's axis of rotation meets its surface...
in a logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
. On the mercator projection
Mercator projection
The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...
such a course is a straight line, as the north and south poles project to infinity. The angle that the loxodrome subtends relative to the lines of longitude (i.e. its slope, the "tightness" of the spiral) is the argument of k. Of course, Möbius transformations may have their two fixed points anywhere, not just at the north and south poles. But any loxodromic transformation will be conjugate to a transform that moves all points along such loxodromes.
If we take the one-parameter subgroup
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
generated by any loxodromic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of curves, away from the first fixed point and toward the second fixed point. Unlike the hyperbolic case, these curves are not circular arcs, but certain curves which under stereographic projection from the sphere to the plane appear as spiral curves which twist counterclockwise infinitely often around one fixed point and twist clockwise infinitely often around the other fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
You can probably guess the physical interpretation in the case when the two fixed points are
 : an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points
: an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points  , and with
, and with  determined respectively by the magnitude of the actual linear and angular velocities.
determined respectively by the magnitude of the actual linear and angular velocities.Stereographic projection
These images show Möbius transformations stereographically projectedStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
onto the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. Note in particular that when projected onto a sphere, the special case of a fixed point at infinity looks no different from having the fixed points in an arbitrary location.
| One fixed point at infinity | ||
| Fixed points diametrically opposite | ||
| Fixed points in an arbitrary location | ||
Iterating a transformation
If a transformation has fixed points
has fixed points  , and characteristic constant k, then
, and characteristic constant k, then  will have
will have  ,
,  ,
,  .
.This can be used to iterate a transformation, or to animate one by breaking it up into steps.
These images show three points (red, blue and black) continuously iterated under transformations with various characteristic constants.
 |
 |
 |
|
And these images demonstrate what happens when you transform a circle under Hyperbolic, Elliptical, and Loxodromic transforms. Note that in the elliptical and loxodromic images, the α value is 1/10 .



In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Möbius transformation of the plane is a rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
of the form

of one complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
variable z; here the coefficients a, b, c, d are complex numbers satisfying ad − bc ≠ 0.
Möbius transformations are named in honor of August Ferdinand Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
, although they are also called homographic transformations, linear fractional transformations, or fractional linear transformations.
Overview
Möbius transformations are defined on the extended complex planeRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
(i.e. the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
augmented by the point at infinity):

This extended complex plane can be thought of as a sphere, the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, or as the complex projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
. Every Möbius transformation is a bijective conformal
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
map of the Riemann sphere to itself. Indeed, every such map is by necessity a Möbius transformation.
The set of all Möbius transformations forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
called the Möbius group. It is the automorphism group of the Riemann sphere (when considered as a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
) and is sometimes denoted
 .
.The Möbius group is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the group of orientation-preserving isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of hyperbolic 3-space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
and therefore plays an important role when studying hyperbolic 3-manifold
Hyperbolic 3-manifold
A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously...
s.
In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
acts on the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
in the same way that the Möbius group acts on the Riemann sphere. In fact, these two groups are isomorphic. An observer who accelerates to relativistic velocities will see the pattern of constellations as seen near the Earth continuously transform according to infinitesimal Möbius transformations. This observation is often taken as the starting point of twistor theory
Twistor theory
In theoretical and mathematical physics, twistor theory maps the geometric objects of conventional 3+1 space-time into geometric objects in a 4 dimensional space with metric signature...
.
Certain subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of the Möbius group form the automorphism groups of the other simply-connected Riemann surfaces (the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
and the hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
). As such, Möbius transformations play an important role in the theory of Riemann surfaces. The fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of every Riemann surface is a discrete subgroup of the Möbius group (see Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
and Kleinian group
Kleinian group
In mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
).
A particularly important discrete subgroup of the Möbius group is the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
; it is central to the theory of many fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s, modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s, elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s and Pellian equations.
Möbius transformations can be more generally defined in spaces of dimension n>2 as the bijective conformal orientation-preserving maps from the n-sphere to the n-sphere. Such a transformation is the most general form of conformal mapping of a domain. According to Liouville's theorem a Möbius transformation can be expressed as a composition of translations, similarities, orthogonal transformations and inversions.
Definition
The general form of a Möbius transformation is given by
where a, b, c, d are any complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s satisfying ad − bc ≠ 0. (If ad = bc the rational function defined above is a constant and is not considered a Möbius transformation.) In case c≠0 this definition is extended to the whole Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
by defining

if c=0 we define

This turns f(z) into a bijective holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
from the Riemann sphere to the Riemann sphere.
The set of all Möbius transformations forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. This group can be given the structure of a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
in such a way that composition and inversion are holomorphic maps. The Möbius group is then a complex Lie group. The Möbius group is usually denoted
 as it is the automorphism group of the Riemann sphere.
as it is the automorphism group of the Riemann sphere.Decomposition and elementary properties
A Möbius transformation is equivalent to a sequence of simpler transformations. Let:-
 (translationTranslation (geometry)In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
(translationTranslation (geometry)In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
by d/c) -
 (inversionInversion (geometry)In geometry, inversive geometry is the study of those properties of figures that are preserved by a generalization of a type of transformation of the Euclidean plane, called inversion...
(inversionInversion (geometry)In geometry, inversive geometry is the study of those properties of figures that are preserved by a generalization of a type of transformation of the Euclidean plane, called inversion...
and reflectionReflection (mathematics)In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
with respect to the real axis) -
 (dilationDilation (mathematics)In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
(dilationDilation (mathematics)In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
and rotationRotation (mathematics)In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
) -
 (translation by a/c)
(translation by a/c)
then these functions can be composed
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, giving

This decomposition makes many properties of the Möbius transformation obvious.
The existence of the inverse Möbius transformation and its explicit formula are easily derived by the composition of the inverse functions of the simpler transformations. That is, define functions
 such that each
such that each  is the inverse of
is the inverse of  . Then the composition
. Then the composition
gives a formula for the inverse.
Preservation of angles and generalized circles
From this decomposition, we see that Möbius transformations carry over all non-trivial properties of circle inversion. For example, the preservation of angles is reduced to proving that circle inversion preserves angles since the other types of transformations are dilation and isometries (translation, reflection, rotation), which trivially preserve angles.Furthermore, Möbius transformations map generalized circles to generalized circles since circle inversion has this property. A generalized circle is either a circle or a line, the latter being considered as a circle through the point at infinity. Note that a Möbius transformation does not necessarily map circles to circles and lines to lines: it can mix the two. Even if it maps a circle to another circle, it does not necessarily map the first circle's center to the second circle's center.
Cross-ratio preservation
Cross-ratioCross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
s are invariant under Möbius transformations. That is, if a Möbius transformation maps four distinct points
 to four distinct points
to four distinct points  respectively, then
respectively, then
If one of the points
 is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of
is the point at infinity, then the cross-ratio has to be defined by taking the appropriate limit; e.g. the cross-ratio of  is
is
Projective matrix representations
With every invertible complex 2-by-2 matrix
we can associate the Möbius transformation

The condition ad − bc ≠ 0 is equivalent to the condition that the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of above matrix be nonzero, i.e. that the matrix be invertible.
It is straightforward to check that then the product
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
of two matrices will be associated with the composition of the two corresponding Möbius transformations.
In other words, the map

from the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(2,C) to the Möbius group,
which sends the matrix
 to the transformation f, is a group homomorphism
to the transformation f, is a group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
.
Note that any matrix obtained by multiplying
 by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up to
by a complex scalar λ determines the same transformation, so a Möbius transformation determines its matrix only up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
scalar multiples. In other words: the kernel of π consists of all scalar multiples of the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
I, and the first isomorphism theorem of group theory states that the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
GL(2,C)/(CI) is isomorphic to the Möbius group. This quotient group is known as the projective linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
and is usually denoted PGL(2,C).

The same identification of PGL(2,K) with the group of fractional linear transformations and with the group of projective linear automorphisms of the projective line holds over any field K, a fact of algebraic interest, particularly for finite fields, though the case of the complex numbers has the greatest geometric interest.
The natural action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of PGL(2,C) on the complex projective line CP1 is exactly the natural action of the Möbius group on the Riemann sphere, where the projective line CP1 and the Riemann sphere are identified as follows:

Here [z1:z2] are homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
on CP1; the point [1:0] corresponds to the point ∞ of the Riemann sphere.
By using homogeneous coordinates, many concrete calculations involving Möbius transformations can be simplified, since no case distinctions dealing with ∞ are required.
If one restricts
 to matrices of determinant one, the map
to matrices of determinant one, the map  restricts to a surjective map from the special linear group
restricts to a surjective map from the special linear groupSpecial linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2,C) to the Möbius group; in the restricted setting the kernel is formed by plus and minus the identity, and the quotient group SL(2,C)/{±I}, denoted by PSL(2,C), is therefore also isomorphic to the Möbius group:

From this we see that the Möbius group is a 3-dimensional complex Lie group (or a 6-dimensional real Lie group). It is a semisimple non-compact
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
Lie group.
Note that there are precisely two matrices with unit determinant which can be used to represent any given Möbius transformation. That is, SL(2,C) is a double cover of PSL(2,C). Since SL(2,C) is simply-connected it is the universal cover of the Möbius group. Therefore the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the Möbius group is Z2.
Specifying a transformation by three points
Given a set of three distinct points z1, z2, z3 on the Riemann sphere and a second set of distinct points w1, w2, w3, there exists precisely one Möbius transformation f(z) which maps the zs to the ws, i.e. with f(zi) = wi for i=1,2,3. (In other words: the actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the Möbius group on the Riemann sphere is sharply 3-transitive.) There are several ways to determine f(z) from the given sets of points.
Mapping first to 0, 1, ∞
It is easy to check that the Möbius transformation
with matrix

maps z1, z2, z3 to 0, 1, ∞, respectively.
(If one of the zi is ∞, then the proper formula for
 is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)
is obtained from the above one by first dividing all entries by zi and then taking the limit zi→∞.)If
 is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix
is similarly defined to map w1, w2, w3 to 0, 1, ∞, then the matrix  which maps
which maps  to
to  becomes
becomes
Explicit determinant formula
The equation
is equivalent to the equation of a standard hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...

in the (z,w)-plane. The problem of constructing a Möbius transformation
 mapping a triple
mapping a triple  to another triple
to another triple  is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points
is thus equivalent to finding the coefficients a, b, c, d of the hyperbola passing through the points  . An explicit equation can be found by evaluating the determinant
. An explicit equation can be found by evaluating the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

by means of a Laplace expansion
Laplace expansion
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of...
along the first row. This results in the determinant formulae




for the coefficients
 of the representing matrix
of the representing matrix  . The constructed matrix
. The constructed matrix  has determinant equal to
has determinant equal to  which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.
which does not vanish if the zi resp. wi are pairwise different thus the Möbius transformation is well-defined. If one of the points zi or wi is ∞, then we first divide all four determinants by this variable and then take the limit as the variable approaches ∞.Classification
Non-identity Möbius transformations are commonly classified into four types, parabolic, elliptic, hyperbolic and loxodromic, with the hyperbolic ones being a subclass of the loxodromic ones. The classification has both algebraic and geometric significance. Geometrically, the different types result in different transformations of the complex plane, as the figures below illustrate.The four types can be distinguished by looking at the trace
 . Note that the trace is invariant under conjugation
. Note that the trace is invariant under conjugationConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
, that is,

and so every member of a conjugacy class will have the same trace. Every Möbius transformation can be written such that its representing matrix
 has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations
has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations  (both not equal to the identity transform) with
(both not equal to the identity transform) with  are conjugate if and only if
are conjugate if and only if 
In the following discussion we will always assume that the representing matrix
 is normalized such that
is normalized such that  .
.Parabolic transforms
A non-identity Möbius transformation defined by a matrix of determinant one is said to be parabolic if
of determinant one is said to be parabolic if
(so the trace is plus or minus 2; either can occur for a given transformation since
 is determined only up to sign). In fact one of the choices for
is determined only up to sign). In fact one of the choices for  has the same characteristic polynomial
has the same characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
X2−2X+1 as the identity matrix, and is therefore unipotent
Unipotent
In mathematics, a unipotent element r of a ring R is one such that r − 1 is a nilpotent element, in other words such that some power n is zero....
. A Möbius transform is parabolic if and only if it has exactly one fixed point in the extended complex plane
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
 , which happens if and only if it can be defined by a matrix conjugate to
, which happens if and only if it can be defined by a matrix conjugate toConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...

which describes a translation in the complex plane.
The set of all parabolic Möbius transformations with a given fixed point in
 , together with the identity, forms a subgroup
, together with the identity, forms a subgroupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
isomorphic to the group of matrices

this is an example of the unipotent radical
Unipotent
In mathematics, a unipotent element r of a ring R is one such that r − 1 is a nilpotent element, in other words such that some power n is zero....
of a Borel subgroup
Borel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
(of the Möbius group, or of SL(2,C) for the matrix group; the notion is defined for any reductive Lie group).
Characteristic constant
All non-parabolic transformations have two fixed points and are defined by a matrix conjugate to
with the complex number
 not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number
not equal to 0, 1 or −1, corresponding to a dilation/rotation through multiplication by the complex number  , called the characteristic constant or multiplier of the transformation.
, called the characteristic constant or multiplier of the transformation.Elliptic transforms
The transformation is said to be elliptic if it can be represented by a matrix whose trace is real
whose trace is realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
with

A transform is elliptic if and only if
 . Writing
. Writing  , an elliptic transform is conjugate to
, an elliptic transform is conjugate to
with
 real.
real.Note that for any
 with characteristic constant k, the characteristic constant of
with characteristic constant k, the characteristic constant of  is
is  . Thus, all Möbius transformations of finite order
. Thus, all Möbius transformations of finite orderOrder (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
are elliptic transformations, namely exactly those where λ is a root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, or, equivalently, where α is a rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
multiple of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
.
Hyperbolic transforms
The transform is said to be hyperbolic if it can be represented by a matrix whose trace is real
whose trace is realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
with

A transform is hyperbolic if and only if λ is real and positive.
Loxodromic transforms
The transform is said to be loxodromic if is not in [0,4]. A transformation is loxodromic if and only if
is not in [0,4]. A transformation is loxodromic if and only if  .
.Historically, navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
by loxodrome or rhumb line
Rhumb line
In navigation, a rhumb line is a line crossing all meridians of longitude at the same angle, i.e. a path derived from a defined initial bearing...
refers to a path of constant bearing
Bearing (navigation)
In marine navigation, a bearing is the direction one object is from another object, usually, the direction of an object from one's own vessel. In aircraft navigation, a bearing is the actual compass direction of the forward course of the aircraft...
; the resulting path is a logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
, similar in shape to the transformations of the complex plane that a loxodromic Möbius transformation makes. See the geometric figures below.
General classification
| Transformation | Trace squared | Multipliers | Class representative | |
|---|---|---|---|---|
| Elliptic |  |
 |
 |
 |
| Parabolic |  |
 |
 |
 |
| Hyperbolic |  |
  |
 |
 |
| Loxodromic |  |
 |
 |
 |
The real case and a note on terminology
Over the real numbers (if the coefficients must be real), there are no non-hyperbolic loxodromic transformations, and the classification is into elliptic, parabolic, and hyperbolic, as for real conics. The terminology is due to considering half the absolute value of the trace, as the eccentricity
as the eccentricityEccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
of the transformation – division by 2 corrects for the dimension, so the identity has eccentricity 1 (tr/n is sometimes used as an alternative for the trace for this reason), and absolute value corrects for the trace only being defined up to a factor of
 due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.
due to working in PSL. Alternatively one may use half the trace squared as a proxy for the eccentricity squared, as was done above; these classifications (but not the exact eccentricity values, since squaring and absolute values are different) agree for real traces but not complex traces. The same terminology is used for the classification of elements of SL2(R) (the 2-fold cover), and analogous classifications are used elsewhere. Loxodromic transformations are an essentially complex phenomenon, and correspond to complex eccentricities.Fixed points
Every non-identity Möbius transformation has two fixed pointsFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
 on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.
on the Riemann sphere. Note that the fixed points are counted here with multiplicity; the parabolic transformations are those where the fixed points coincide. Either or both of these fixed points may be the point at infinity.Determining the fixed points
The fixed points of the transformation
are obtained by solving the fixed point equation
 . For
. For  , this has two roots obtained by expanding this equation to
, this has two roots obtained by expanding this equation to
and applying the quadratic formula. The roots are

Note that for parabolic transformations, which satisfy
 , the fixed points coincide. Note also that the discriminant is
, the fixed points coincide. Note also that the discriminant is
When c = 0, the quadratic equation degenerates into a linear equation. This corresponds to the situation that one of the fixed points is the point at infinity. When a ≠ d the second fixed point is finite and is given by

In this case the transformation will be a simple transformation composed of translation
Translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
s, rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s, and dilations
Dilation (mathematics)
In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
:

If c = 0 and a = d, then both fixed points are at infinity, and the Möbius transformation corresponds to a pure translation:
 .
.Topological proof
Topologically, the fact that (non-identity) Möbius transformations fix 2 points corresponds to the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the sphere being 2:

Firstly, the projective linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
PGL(2,K) is sharply 3-transitive – for any two ordered triples of distinct points, there is a unique map that takes one triple to the other, just as for Möbius transforms, and by the same algebraic proof (essentially dimension counting, as the group is 3-dimensional). Thus any map that fixes at least 3 points is the identity.
Next, the Möbius group is connected, so any map is homotopic to the identity. The Lefschetz–Hopf theorem states that the sum of the indices (in this context, multiplicity) of the fixed points of a map with finitely many fixed points equals the Lefschetz number of the map, which is this case is the trace of the identity map on homology groups, which is simply the Euler characteristic.
By contrast, the projective linear group of the real projective line, PGL(2,R) need not fix any points – for example
 has no (real) fixed points: as a complex transformation it fixes
has no (real) fixed points: as a complex transformation it fixes  Geometrically this map is the stereographic projection
Geometrically this map is the stereographic projectionStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
of a rotation by 90° around
 with period 4, which takes
with period 4, which takes  – while the map
– while the map  fixes the two points of 0 and
fixes the two points of 0 and  This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.
This corresponds to the fact that the Euler characteristic of the circle (real projective line) is 0, and thus the Lefschetz fixed-point theorem says only that it must fix at least 0 points, but possibly more.Normal form
Möbius transformations are also sometimes written in terms of their fixed points in so-called normal form. We first treat the non-parabolic case, for which there are two distinct fixed points.Non-parabolic case:
Every non-parabolic transformation is conjugate
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
to a dilation/rotation, i.e. a transformation of the form

(k ∈ C) with fixed points at 0 and ∞. To see this define a map

which sends the points
 to
to  . Here we assume that both
. Here we assume that both  and
and  are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.
are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.If f has distinct fixed points
 then the transformation
then the transformation  has fixed points at 0 and ∞ and is therefore a dilation:
has fixed points at 0 and ∞ and is therefore a dilation:  . The fixed point equation for the transformation f can then be written
. The fixed point equation for the transformation f can then be written
Solving for f gives (in matrix form):

or, if one of the fixed points is at infinity:

From the above expressions one can calculate the derivatives of f at the fixed points:
 and
and 
Observe that, given an ordering of the fixed points, we can distinguish one of the multipliers (k) of f as the characteristic constant of f. Reversing the order of the fixed points is equivalent to taking the inverse multiplier for the characteristic constant:

For loxodromic transformations, whenever
 , one says that
, one says that  is the repulsive fixed point, and
is the repulsive fixed point, and  is the attractive fixed point. For
is the attractive fixed point. For  , the roles are reversed.
, the roles are reversed.Parabolic case:
In the parabolic case there is only one fixed point
 . The transformation sending that point to ∞ is
. The transformation sending that point to ∞ is
or the identity if
 is already at infinity. The transformation
is already at infinity. The transformation  fixes infinity and is therefore a translation:
fixes infinity and is therefore a translation:
Here, β is called the translation length. The fixed point formula for a parabolic transformation is then

Solving for f (in matrix form) gives

or, if
 :
:
Note that
 is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:
is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:
Geometric interpretation of the characteristic constant
The following picture depicts (after stereographic transformation from the sphere to the plane) the two fixed points of a Möbius transformation in the non-parabolic case:
The characteristic constant can be expressed in terms of its logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
:

When expressed in this way, the real number
 becomes an expansion factor. It indicates how repulsive the fixed point
becomes an expansion factor. It indicates how repulsive the fixed point  is, and how attractive
is, and how attractive  is.
is.The real number
 is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about
is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about  and clockwise about
and clockwise about  .
.Elliptic transformations
If , then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.
, then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptic. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.If we take the one-parameter subgroup generated by any elliptic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a family of circles which is nested between the two fixed points on the Riemann sphere. In general, the two fixed points can be any two distinct points.
This has an important physical interpretation.
Imagine that some observer rotates with constant angular velocity about some axis. Then we can take the two fixed points to be the North and South poles of the celestial sphere. The appearance of the night sky is now transformed continuously in exactly the manner described by the one-parameter subgroup of elliptic transformations sharing the fixed points
 , and with the number
, and with the number  corresponding to the constant angular velocity of our observer.
corresponding to the constant angular velocity of our observer.Here are some figures illustrating the effect of an elliptic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):


These pictures illustrate the effect of a single Möbius transformation. The one-parameter subgroup which it generates continuously moves points along the family of circular arcs suggested by the pictures.
Hyperbolic transformations

 is zero (or a multiple of
is zero (or a multiple of  ), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.
), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.If we take the one-parameter subgroup
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
generated by any hyperbolic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of circular arcs away from the first fixed point and toward the second fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
This too has an important physical interpretation. Imagine that an observer accelerates (with constant magnitude of acceleration) in the direction of the North pole on his celestial sphere. Then the appearance of the night sky is transformed in exactly the manner described by the one-parameter subgroup of hyperbolic transformations sharing the fixed points
 , with the real number
, with the real number  corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).
corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).Here are some figures illustrating the effect of a hyperbolic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):


These pictures resemble the field lines of a positive and a negative electrical charge located at the fixed points, because the circular flow lines subtend a constant angle between the two fixed points.
Loxodromic transformations
If both ρ and α are nonzero, then the transformation is said to be loxodromic. These transformations tend to move all points in S-shaped paths from one fixed point to the other.The word "loxodrome" is from the Greek: "λοξος (loxos), slanting + δρόμος (dromos), course". When sailing
Sailing
Sailing is the propulsion of a vehicle and the control of its movement with large foils called sails. By changing the rigging, rudder, and sometimes the keel or centre board, a sailor manages the force of the wind on the sails in order to move the boat relative to its surrounding medium and...
on a constant bearing
Bearing (navigation)
In marine navigation, a bearing is the direction one object is from another object, usually, the direction of an object from one's own vessel. In aircraft navigation, a bearing is the actual compass direction of the forward course of the aircraft...
- if you maintain a heading of (say) north-east, you will eventually wind up sailing around the north pole
North Pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is, subject to the caveats explained below, defined as the point in the northern hemisphere where the Earth's axis of rotation meets its surface...
in a logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
. On the mercator projection
Mercator projection
The Mercator projection is a cylindrical map projection presented by the Belgian geographer and cartographer Gerardus Mercator, in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known as rhumb lines or loxodromes, as...
such a course is a straight line, as the north and south poles project to infinity. The angle that the loxodrome subtends relative to the lines of longitude (i.e. its slope, the "tightness" of the spiral) is the argument of k. Of course, Möbius transformations may have their two fixed points anywhere, not just at the north and south poles. But any loxodromic transformation will be conjugate to a transform that moves all points along such loxodromes.
If we take the one-parameter subgroup
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
generated by any loxodromic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of curves, away from the first fixed point and toward the second fixed point. Unlike the hyperbolic case, these curves are not circular arcs, but certain curves which under stereographic projection from the sphere to the plane appear as spiral curves which twist counterclockwise infinitely often around one fixed point and twist clockwise infinitely often around the other fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.
You can probably guess the physical interpretation in the case when the two fixed points are
 : an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points
: an observer who is both rotating (with constant angular velocity) about some axis and moving along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points  , and with
, and with  determined respectively by the magnitude of the actual linear and angular velocities.
determined respectively by the magnitude of the actual linear and angular velocities.Stereographic projection
These images show Möbius transformations stereographically projectedStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
onto the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. Note in particular that when projected onto a sphere, the special case of a fixed point at infinity looks no different from having the fixed points in an arbitrary location.
| One fixed point at infinity | ||
| Fixed points diametrically opposite | ||
| Fixed points in an arbitrary location | ||
Iterating a transformation
If a transformation has fixed points
has fixed points  , and characteristic constant k, then
, and characteristic constant k, then  will have
will have  ,
,  ,
,  .
.This can be used to iterate a transformation, or to animate one by breaking it up into steps.
These images show three points (red, blue and black) continuously iterated under transformations with various characteristic constants.
 |
 |
 |
|
And these images demonstrate what happens when you transform a circle under Hyperbolic, Elliptical, and Loxodromic transforms. Note that in the elliptical and loxodromic images, the α value is 1/10 .







