
Nested word
Encyclopedia
In computer science
, more specifically in automata
and formal language
theory, nested words are a concept proposed by Alur
and Madhusudan as a joint generalization of words
, as traditionally used for modelling linearly ordered structures, and of ordered unranked trees
, as traditionally used for modelling hierarchical structures. Finite-state acceptors for nested words,
so-called nested word automata, then give a more expressive generalization of finite automata on words. The linear encodings of languages accepted by finite nested word automata gives the class of visibly pushdown languages. The latter language class lies properly between the regular language
s and the deterministic context-free language
s. Since their introduction in 2004, these concepts have triggered much research in that area.
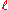 , we use the notation
, we use the notation  to denote the set
to denote the set 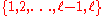 , with the special case
, with the special case  .
.
A matching relation ↝ of length is a subset of
is a subset of  such that:
such that:
(i) all nesting edges are forward, that is, if i ↝ j then i
(ii) nesting edges never have a finite position in common, that is, for , there is at most one position h such that h ↝ i, and there is at most one position j such that i ↝ j; and
, there is at most one position h such that h ↝ i, and there is at most one position j such that i ↝ j; and
(iii) nesting edges never cross, that is, we can't find i
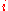 is referred to as a call position, if i ↝ j for some j, as a pending call if i ↝ ∞, as a return position, if h ↝ i for some h and as a "pending return" if -∞ ↝ i.
is referred to as a call position, if i ↝ j for some j, as a pending call if i ↝ ∞, as a return position, if h ↝ i for some h and as a "pending return" if -∞ ↝ i.
A nested word of length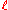 over an alphabet Σ is a pair (w,↝), where w is a word of length
over an alphabet Σ is a pair (w,↝), where w is a word of length 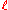 over Σ (in the usual sense) and ↝ is a matching relation of length
over Σ (in the usual sense) and ↝ is a matching relation of length 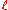 .
.
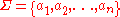 can be encoded into "ordinary" words over the tagged alphabet
can be encoded into "ordinary" words over the tagged alphabet  , in which each symbol a from Σ has three tagged counterparts: the
, in which each symbol a from Σ has three tagged counterparts: the
symbol ⟨a for encoding a call position in a nested word labelled with a, the symbol a⟩ for encoding a return position labelled with a, and finally the symbol a itself for representing an internal position labelled with a. More precisely, let φ be the function mapping nested words over Σ to words over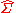 such that each nested word (
such that each nested word (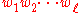 ,↝) is mapped to the word
,↝) is mapped to the word 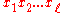 , where the letter
, where the letter 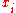 equals ⟨a, a, or a⟩, respectively, if
equals ⟨a, a, or a⟩, respectively, if  and i is a call position, an internal position, or a return position, respectively.
and i is a call position, an internal position, or a return position, respectively.
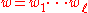 from left to right, and the state of the automaton after reading the jth letter
from left to right, and the state of the automaton after reading the jth letter  depends on the state in which the automaton was before reading
depends on the state in which the automaton was before reading 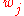 .
.
In a nested word automaton, the position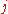 in the nested word (w,↝) might be a return position; if so, the state after reading
in the nested word (w,↝) might be a return position; if so, the state after reading 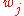 will not only depend on the linear state in which the automaton was before reading
will not only depend on the linear state in which the automaton was before reading 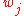 , but also on a hierarchical state propagated by the automaton at the time it was in the corresponding call position. In analogy to regular language
, but also on a hierarchical state propagated by the automaton at the time it was in the corresponding call position. In analogy to regular language
s of words, a set L of nested words is called regular if it is accepted by some (finite-state) nested word automaton.
.
Following Alur and Madhusudan, a deterministic visibly pushdown automaton is formally defined as a 6-tuple
where
The notion of computation of a visibly pushdown automaton is a restriction of the one used for pushdown automata. Visibly pushdown automata only add a symbol to the stack when reading a call symbol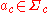 , they only remove the top element from the stack when reading a return symbol
, they only remove the top element from the stack when reading a return symbol  and they do not alter the stack when reading an internal event
and they do not alter the stack when reading an internal event 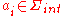 . A computation ending in an accepting state is an accepting computation.
. A computation ending in an accepting state is an accepting computation.
As a result, a visibly pushdown automaton cannot push to and pop from the stack with the same input symbol. Thus the language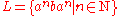 cannot be accepted by a visibly pushdown automaton for any partition of
cannot be accepted by a visibly pushdown automaton for any partition of  , however there are pushdown automata accepting this language.
, however there are pushdown automata accepting this language.
If a language
L over a tagged alphabet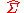 is accepted by a deterministic visibly pushdown automaton, then L is called a visibly pushdown language.
is accepted by a deterministic visibly pushdown automaton, then L is called a visibly pushdown language.
 states, the deterministic one may have up to
states, the deterministic one may have up to 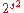 states.
states.
 be the size of the description of an automaton
be the size of the description of an automaton  , then it is possible to check if a word n is accepted by the automaton in time
, then it is possible to check if a word n is accepted by the automaton in time 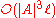 . In particular, the emptiness problem is solvable in time
. In particular, the emptiness problem is solvable in time 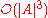 .
.
If is fixed, it is decidable in time
is fixed, it is decidable in time 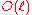 and space
and space 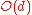 where
where 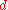 is the depth of n in a streaming seeing. It is also decidable with space
is the depth of n in a streaming seeing. It is also decidable with space 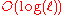 and time
and time 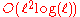 , and by a uniform boolean circuit of depth
, and by a uniform boolean circuit of depth 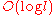 .
.
For two nondeterministic automata A and B, deciding whether the set of words accepted by A is a subset of the word accepted by B is EXPTIME
-complete. It is also EXPTIME-complete to figure out if there is a word that is not accepted.
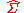 forms a subset of the set DCFL of deterministic context-free language
forms a subset of the set DCFL of deterministic context-free language
s over the set of symbols in . In particular, the function that removes matching relation from nested words transforms regular languages over nested words into context-free languages.
. In particular, the function that removes matching relation from nested words transforms regular languages over nested words into context-free languages.
For the intersection operation, one can construct a VPA M simulating two given VPAs and
and  by a simple product construction : For
by a simple product construction : For  , assume
, assume 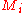 is given as
is given as 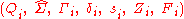 . Then for the automaton M, the set of states is
. Then for the automaton M, the set of states is 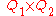 , the initial state is
, the initial state is 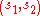 , the set of final states is
, the set of final states is  , the stack alphabet is given by
, the stack alphabet is given by  , and the initial stack symbol is
, and the initial stack symbol is 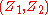 .
.
If is in state
is in state 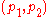 on reading a call symbol
on reading a call symbol  , then
, then
 pushes the stack symbol
pushes the stack symbol 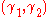
and goes to state , where
, where 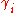 is the stack symbol pushed by
is the stack symbol pushed by 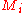
when transitioning from state to
to  on reading input
on reading input  .
.
If is in state
is in state  on reading an internal symbol
on reading an internal symbol  , then
, then 
goes to state , whenever
, whenever 
transitions from state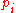 to
to 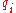 on reading a.
on reading a.
If is in state
is in state 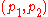 on reading a return symbol
on reading a return symbol 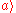 , then
, then 
pops the symbol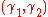 from the stack and
from the stack and
goes to state , where
, where 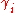 is the stack symbol popped by
is the stack symbol popped by 
when transitioning from state to
to 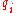 on reading
on reading  .
.
Correctness of the above construction crucially relies on the fact that the push and pop actions of the simulated
machines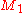 and
and  are synchronized along the input symbols read. In fact, a similar simulation is no longer possible for deterministic pushdown automata
are synchronized along the input symbols read. In fact, a similar simulation is no longer possible for deterministic pushdown automata
, as the larger class of deterministic context-free languages is no longer closed under intersection.
In contrast to the construction for concatenation shown above, the complementation construction for visibly pushdown automata parallels the standard construction for deterministic pushdown automata.
Moreover, the class of visibly pushdown languages is closed under
s, which were introduced by . In comparison to conjunctive grammars, a generalization of context-free grammars, shows that the linear conjunctive languages form a superclass of the visibly pushdown languages. The following table puts the family of visibly pushdown languages in relation to other language families in the Chomsky hierarchy
.
Visibly pushdown grammars can be defined as a restriction of context-free grammars. A visibly pushdown grammars G is defined by the 4-tuple
:
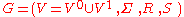 where
where
Here, the asterisk represents the Kleene star
operation and is the empty word.
is the empty word.
 .
.
SO (complexity)
with two unary predicates call and return, linear successor and the matching relation ↝.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, more specifically in automata
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
and formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
theory, nested words are a concept proposed by Alur
Rajeev Alur
Rajeev Alur is a researcher in the field of formal methods for modeling and analyzing programs and systems, in particular model checking. His contributions include timed automation and temporal specifications based on languages of nested words and trees. He is Zisman Family professor of Computer...
and Madhusudan as a joint generalization of words
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
, as traditionally used for modelling linearly ordered structures, and of ordered unranked trees
Tree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
, as traditionally used for modelling hierarchical structures. Finite-state acceptors for nested words,
so-called nested word automata, then give a more expressive generalization of finite automata on words. The linear encodings of languages accepted by finite nested word automata gives the class of visibly pushdown languages. The latter language class lies properly between the regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s and the deterministic context-free language
Deterministic context-free language
A deterministic context-free language is a formal language which is defined by a deterministic context-free grammar. The set of deterministic context-free languages is called DCFL and is identical to the set of languages accepted by a deterministic pushdown automaton.The set of deterministic...
s. Since their introduction in 2004, these concepts have triggered much research in that area.
Formal definition
To define nested words, we first need to define matching relation. As usual, for a nonnegative integer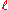 , we use the notation
, we use the notation  to denote the set
to denote the set 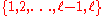 , with the special case
, with the special case  .
.A matching relation ↝ of length
 is a subset of
is a subset of  such that:
such that: (i) all nesting edges are forward, that is, if i ↝ j then i
(ii) nesting edges never have a finite position in common, that is, for
 , there is at most one position h such that h ↝ i, and there is at most one position j such that i ↝ j; and
, there is at most one position h such that h ↝ i, and there is at most one position j such that i ↝ j; and (iii) nesting edges never cross, that is, we can't find i
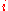 is referred to as a call position, if i ↝ j for some j, as a pending call if i ↝ ∞, as a return position, if h ↝ i for some h and as a "pending return" if -∞ ↝ i.
is referred to as a call position, if i ↝ j for some j, as a pending call if i ↝ ∞, as a return position, if h ↝ i for some h and as a "pending return" if -∞ ↝ i.A nested word of length
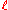 over an alphabet Σ is a pair (w,↝), where w is a word of length
over an alphabet Σ is a pair (w,↝), where w is a word of length 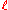 over Σ (in the usual sense) and ↝ is a matching relation of length
over Σ (in the usual sense) and ↝ is a matching relation of length 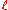 .
.Encoding nested words into ordinary words
Nested words over the alphabet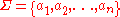 can be encoded into "ordinary" words over the tagged alphabet
can be encoded into "ordinary" words over the tagged alphabet  , in which each symbol a from Σ has three tagged counterparts: the
, in which each symbol a from Σ has three tagged counterparts: thesymbol ⟨a for encoding a call position in a nested word labelled with a, the symbol a⟩ for encoding a return position labelled with a, and finally the symbol a itself for representing an internal position labelled with a. More precisely, let φ be the function mapping nested words over Σ to words over
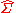 such that each nested word (
such that each nested word (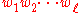 ,↝) is mapped to the word
,↝) is mapped to the word 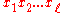 , where the letter
, where the letter 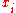 equals ⟨a, a, or a⟩, respectively, if
equals ⟨a, a, or a⟩, respectively, if  and i is a call position, an internal position, or a return position, respectively.
and i is a call position, an internal position, or a return position, respectively.Example
For illustration, let n=(w,↝) be the nested word over an ternary alphabet with w=abaabccca and matching relation ↝ = {(-∞,1),(2,∞),(3,4),(5,7),(8,∞)}. Then its encoding as word reads as φ(n) = a⟩⟨b⟨aa⟩⟨bcc⟩⟨ca.Nested word automaton
A nested word automaton has a finite number of states, and operates in almost the same way as a deterministic finite automaton on classical strings: a classical finite automaton reads the input word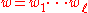 from left to right, and the state of the automaton after reading the jth letter
from left to right, and the state of the automaton after reading the jth letter  depends on the state in which the automaton was before reading
depends on the state in which the automaton was before reading 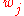 .
.In a nested word automaton, the position
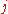 in the nested word (w,↝) might be a return position; if so, the state after reading
in the nested word (w,↝) might be a return position; if so, the state after reading 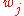 will not only depend on the linear state in which the automaton was before reading
will not only depend on the linear state in which the automaton was before reading 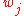 , but also on a hierarchical state propagated by the automaton at the time it was in the corresponding call position. In analogy to regular language
, but also on a hierarchical state propagated by the automaton at the time it was in the corresponding call position. In analogy to regular languageRegular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s of words, a set L of nested words is called regular if it is accepted by some (finite-state) nested word automaton.
Visibly pushdown automaton
Nested word automata are an automaton model accepting nested words. There is an equivalent automaton model operating on (ordinary) words. Namely, the notion of a deterministic visibly pushdown automaton is a restriction of the notion of a deterministic pushdown automatonDeterministic pushdown automaton
In automata theory, a pushdown automaton is a finite automaton with an additional stack of symbols; its transitions can take the top symbol on the stack and depend on its value, and they can add new top symbols to the stack....
.
Following Alur and Madhusudan, a deterministic visibly pushdown automaton is formally defined as a 6-tuple

where
 is a finite set of states,
is a finite set of states, is the input alphabet, which – in contrast to that of ordinary pushdown automata – is partitioned into three sets
is the input alphabet, which – in contrast to that of ordinary pushdown automata – is partitioned into three sets 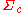 ,
, 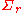 , and
, and  . The alphabet
. The alphabet  denotes the set of call symbols,
denotes the set of call symbols,  contains the return symbols, and the set
contains the return symbols, and the set  contains the internal symbols,
contains the internal symbols, is a finite set which is called the stack alphabet, which containins a special symbol
is a finite set which is called the stack alphabet, which containins a special symbol 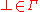 denoting the empty stack,
denoting the empty stack,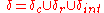 is the transition function, which is partitioned into three parts corresponding to call transitions, return transitions, and internal transitions, namely
is the transition function, which is partitioned into three parts corresponding to call transitions, return transitions, and internal transitions, namely
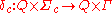 , the call transition function
, the call transition function , the return transition function
, the return transition function , the internal transition function,
, the internal transition function,
 is the initial state, and
is the initial state, and is the set of accepting states.
is the set of accepting states.
The notion of computation of a visibly pushdown automaton is a restriction of the one used for pushdown automata. Visibly pushdown automata only add a symbol to the stack when reading a call symbol
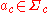 , they only remove the top element from the stack when reading a return symbol
, they only remove the top element from the stack when reading a return symbol  and they do not alter the stack when reading an internal event
and they do not alter the stack when reading an internal event 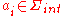 . A computation ending in an accepting state is an accepting computation.
. A computation ending in an accepting state is an accepting computation.As a result, a visibly pushdown automaton cannot push to and pop from the stack with the same input symbol. Thus the language
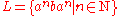 cannot be accepted by a visibly pushdown automaton for any partition of
cannot be accepted by a visibly pushdown automaton for any partition of  , however there are pushdown automata accepting this language.
, however there are pushdown automata accepting this language.If a language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
L over a tagged alphabet
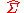 is accepted by a deterministic visibly pushdown automaton, then L is called a visibly pushdown language.
is accepted by a deterministic visibly pushdown automaton, then L is called a visibly pushdown language.Nondeterministic visibly pushdown automata
Nondeterministic visibly pushdown automata are as expressive as deterministic ones. Hence one can transform a nondeterministic visibly pushdown automaton into a deterministic one, but if the nondeterministic automaton had states, the deterministic one may have up to
states, the deterministic one may have up to 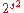 states.
states.Decision problems
Let be the size of the description of an automaton
be the size of the description of an automaton  , then it is possible to check if a word n is accepted by the automaton in time
, then it is possible to check if a word n is accepted by the automaton in time 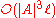 . In particular, the emptiness problem is solvable in time
. In particular, the emptiness problem is solvable in time 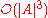 .
.If
 is fixed, it is decidable in time
is fixed, it is decidable in time 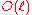 and space
and space 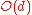 where
where 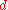 is the depth of n in a streaming seeing. It is also decidable with space
is the depth of n in a streaming seeing. It is also decidable with space 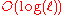 and time
and time 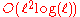 , and by a uniform boolean circuit of depth
, and by a uniform boolean circuit of depth 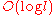 .
.For two nondeterministic automata A and B, deciding whether the set of words accepted by A is a subset of the word accepted by B is EXPTIME
EXPTIME
In computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
-complete. It is also EXPTIME-complete to figure out if there is a word that is not accepted.
Languages
As the definition of visibly pushdown automata shows, deterministic visibly pushdown automata can be seen as a special case of deterministic pushdown automata; thus the set VPL of visibly pushdown languages over forms a subset of the set DCFL of deterministic context-free language
forms a subset of the set DCFL of deterministic context-free languageDeterministic context-free language
A deterministic context-free language is a formal language which is defined by a deterministic context-free grammar. The set of deterministic context-free languages is called DCFL and is identical to the set of languages accepted by a deterministic pushdown automaton.The set of deterministic...
s over the set of symbols in
 . In particular, the function that removes matching relation from nested words transforms regular languages over nested words into context-free languages.
. In particular, the function that removes matching relation from nested words transforms regular languages over nested words into context-free languages.Closure properties
The set of visibly pushdown languages is closed under the following operations:- set operations:
- union
- intersection
- complement, thus giving rise to a boolean algebraBoolean algebraIn abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets...
.
- Kleene starKleene starIn mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
- concatenation
For the intersection operation, one can construct a VPA M simulating two given VPAs
 and
and  by a simple product construction : For
by a simple product construction : For  , assume
, assume 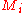 is given as
is given as 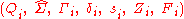 . Then for the automaton M, the set of states is
. Then for the automaton M, the set of states is 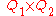 , the initial state is
, the initial state is 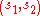 , the set of final states is
, the set of final states is  , the stack alphabet is given by
, the stack alphabet is given by  , and the initial stack symbol is
, and the initial stack symbol is 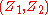 .
.If
 is in state
is in state 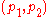 on reading a call symbol
on reading a call symbol  , then
, then pushes the stack symbol
pushes the stack symbol 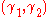
and goes to state
 , where
, where 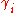 is the stack symbol pushed by
is the stack symbol pushed by 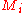
when transitioning from state
 to
to  on reading input
on reading input  .
.If
 is in state
is in state  on reading an internal symbol
on reading an internal symbol  , then
, then 
goes to state
 , whenever
, whenever 
transitions from state
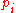 to
to 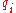 on reading a.
on reading a.If
 is in state
is in state 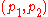 on reading a return symbol
on reading a return symbol 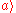 , then
, then 
pops the symbol
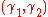 from the stack and
from the stack andgoes to state
 , where
, where 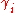 is the stack symbol popped by
is the stack symbol popped by 
when transitioning from state
 to
to 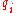 on reading
on reading  .
.Correctness of the above construction crucially relies on the fact that the push and pop actions of the simulated
machines
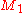 and
and  are synchronized along the input symbols read. In fact, a similar simulation is no longer possible for deterministic pushdown automata
are synchronized along the input symbols read. In fact, a similar simulation is no longer possible for deterministic pushdown automataDeterministic pushdown automaton
In automata theory, a pushdown automaton is a finite automaton with an additional stack of symbols; its transitions can take the top symbol on the stack and depend on its value, and they can add new top symbols to the stack....
, as the larger class of deterministic context-free languages is no longer closed under intersection.
In contrast to the construction for concatenation shown above, the complementation construction for visibly pushdown automata parallels the standard construction for deterministic pushdown automata.
Moreover, the class of visibly pushdown languages is closed under
- prefix closure
- suffix closure
- reversal.
Relation to other language classes
point out that the visibly pushdown languages are more general than the parenthesis languages suggested in . As shown by , the VPL in turn are strictly contained in the class of languages described by operator-precedence grammarOperator-precedence grammar
An operator precedence grammar is a kind of grammar for formal languages.Technically, an operator precedence grammar is a context-free grammar that has the property...
s, which were introduced by . In comparison to conjunctive grammars, a generalization of context-free grammars, shows that the linear conjunctive languages form a superclass of the visibly pushdown languages. The following table puts the family of visibly pushdown languages in relation to other language families in the Chomsky hierarchy
Chomsky hierarchy
Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
.
Visibly pushdown grammars
Visibly pushdown languages are exactly the languages that can be described by visibly pushdown grammars.Visibly pushdown grammars can be defined as a restriction of context-free grammars. A visibly pushdown grammars G is defined by the 4-tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
:
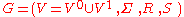 where
where
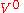 and
and  are disjoint finite set; each element
are disjoint finite set; each element  is called a non-terminal character or a variable. Each variable represents a different type of phrase or clause in the sentence. Each variable defines a sub-language of the language defined by
is called a non-terminal character or a variable. Each variable represents a different type of phrase or clause in the sentence. Each variable defines a sub-language of the language defined by  , and the sub-languages of
, and the sub-languages of 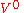 are the one without pending calls or pending returns.
are the one without pending calls or pending returns. is a finite set of terminals, disjoint from
is a finite set of terminals, disjoint from 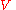 , which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar
, which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar  .
. is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of
is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of 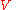 .
. is a finite relation from
is a finite relation from 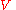 to
to 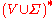 such that
such that 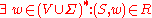 . The members of
. The members of  are called the (rewrite) rules or productions of the grammar. There are three kinds of rewrite rules. For
are called the (rewrite) rules or productions of the grammar. There are three kinds of rewrite rules. For  ,
, 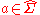 and
and 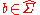

 and if
and if 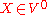 then
then  and
and 
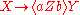 and if
and if  then
then 
Here, the asterisk represents the Kleene star
Kleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
operation and
 is the empty word.
is the empty word.Uniform Boolean circuits
The problem whether a word n is accepted by a given nested word automaton can be solved by uniform Boolean circuits of depth .
.Logical description
Regular languages over nested words are exactly the set of languages described by MonadicMonadic predicate calculus
In logic, the monadic predicate calculus is the fragment of predicate calculus in which all predicate letters are monadic , and there are no function letters...
SO (complexity)
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
with two unary predicates call and return, linear successor and the matching relation ↝.

