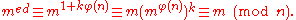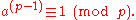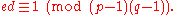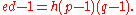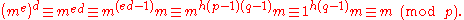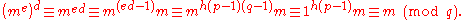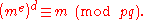RSA
Encyclopedia
RSA is an algorithm
for public-key cryptography
that is based on the presumed difficulty of factoring large integers, the factoring problem. RSA stands for Ron Rivest
, Adi Shamir
and Leonard Adleman
, who first publicly described it in 1978. A user of RSA creates and then publishes the product of two large prime number
s, along with an auxiliary value, as their public key. The prime factors must be kept secret. Anyone can use the public key to encrypt a message, but with currently published methods, if the public key is large enough, only someone with knowledge of the prime factors can feasibly decode the message.
Whether breaking RSA encryption is as hard as factoring is an open question known as the RSA problem
.
, an English mathematician
working for the UK
intelligence agency GCHQ
, described an equivalent system in an internal document in 1973, but given the relatively expensive computers needed to implement it at the time, it was mostly considered a curiosity and, as far as is publicly known, was never deployed. His discovery, however, was not revealed until 1998 due to its top-secret classification, and Rivest, Shamir, and Adleman devised RSA independently of Cocks' work.
The RSA algorithm was publicly described in 1978 by Ron Rivest
, Adi Shamir
, and Leonard Adleman
at MIT
; the letters RSA are the initials of their surnames, listed in the same order as on the paper.
MIT
was granted for a "Cryptographic communications system and method" that used the algorithm in 1983. The patent would have expired on September 21, 2000 (the term of patent
was 17 years at the time), but the algorithm was released to the public domain by RSA Security
on 6 September 2000, two weeks earlier. Since a paper describing the algorithm had been published in August 1977, prior to the December 1977 filing date of the patent application
, regulations in much of the rest of the world precluded patent
s elsewhere and only the US
patent was granted. Had Cocks' work been publicly known, a patent in the US might not have been possible.
From the DWPI's abstract of the patent,
generation, encryption and decryption.
The public key consists of the modulus n and the public (or encryption) exponent e. The private key consists of the modulus n and the private (or decryption) exponent d which must be kept secret.
Notes:
transmits her public key
to Bob
and keeps the private key secret. Bob then wishes to send message M to Alice.
He first turns M into an integer m, such that
by using an agreed-upon reversible protocol known as a padding scheme. He then computes the ciphertext 
corresponding to
This can be done quickly using the method of exponentiation by squaring
. Bob then transmits
to Alice.
Note that at least nine values of m will yield a ciphertext c equal to
m,
But this is very unlikely to occur in practice.
from 
by using her private key exponent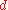 
via computing
Given
, she can recover the original message M by reversing the padding scheme.
(In practice, there are more efficient methods of calculating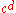
using the pre computed values below.)
The following values are precomputed and stored as part of the private key:
These values allow the recipient to compute the exponentiation
more efficiently as follows:
This is more efficient than computing
even though two modular exponentiations have to be computed.
The reason is that these two modular exponentiations both use a smaller exponent and a smaller modulus.
The public key is (
, 
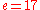). For a padded plaintext
message
, the encryption function is 
.
The private key is (
, 
). For an encrypted ciphertext
, the decryption function is 
.
For instance, in order to encrypt
, we calculate
.
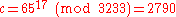To decrypt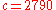
, we calculate
.
Both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation
. In real life situations the primes selected would be much larger; in our example it would be relatively trivial to factor
, 3233, obtained from the freely available public key back to the primes 
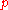and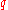 
. Given 
, also from the public key, we could then compute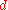 
and so acquire the private key.
Practical implementations use Chinese remainder theorem
to speed up the calculation using modulus of factors (mod p*q using mod p and mod q).
The values dp, dq and qInv, which are part of the private key are computed as follows:
Here is how dp, dq and qInv are used for efficient decryption. (Encryption is efficient by choice of public exponent e)
into the value
before encrypting it. This padding ensures that 
does not fall into the range of insecure plaintexts, and that a given message, once padded, will encrypt to one of a large number of different possible ciphertexts.
Standards such as PKCS#1
have been carefully designed to securely pad messages prior to RSA encryption. Because these schemes pad the plaintext
with some number of additional bits, the size of the un-padded message M must be somewhat smaller. RSA padding schemes must be carefully designed so as to prevent sophisticated attacks which may be facilitated by a predictable message structure. Early versions of the PKCS#1 standard (up to version 1.5) used a construction that turned RSA into a semantically secure encryption scheme. This version was later found vulnerable to a practical adaptive chosen ciphertext attack. Later versions of the standard include Optimal Asymmetric Encryption Padding
(OAEP), which prevents these attacks. The PKCS#1 standard also incorporates processing schemes designed to provide additional security for RSA signatures, e.g., the Probabilistic Signature Scheme for RSA (RSA-PSS).
uses Bob
's public key to send him an encrypted message. In the message, she can claim to be Alice but Bob has no way of verifying that the message was actually from Alice since anyone can use Bob's public key to send him encrypted messages. In order to verify the origin of a message, RSA can also be used to sign
a message.
Suppose Alice wishes to send a signed message to Bob. She can use her own private key to do so. She produces a hash value
of the message, raises it to the power of
(as she does when decrypting a message), and attaches it as a "signature" to the message. When Bob receives the signed message, he uses the same hash algorithm in conjunction with Alice's public key. He raises the signature to the power of 
(as he does when encrypting a message), and compares the resulting hash value with the message's actual hash value. If the two agree, he knows that the author of the message was in possession of Alice's private key, and that the message has not been tampered with since.
Secure padding schemes such as RSA-PSS are as essential for the security of message signing as they are for message encryption. The same key should never be used for both encryption and signing.
and the RSA problem
. Full decryption of an RSA ciphertext is thought to be infeasible on the assumption that both of these problems are hard, i.e., no efficient algorithm exists for solving them. Providing security against partial decryption may require the addition of a secure padding scheme
.
The RSA problem
is defined as the task of taking
th roots modulo a composite 
: recovering a value 
such that 
, where 
is an RSA public key and 
is an RSA ciphertext. Currently the most promising approach to solving the RSA problem is to factor the modulus 
. With the ability to recover prime factors, an attacker can compute the secret exponent 
from a public key 
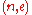, then decrypt 
using the standard procedure. To accomplish this, an attacker factors 
into 
and 
, and computes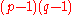 
which allows the determination of 
from 
. No polynomial-time method for factoring large integers on a classical computer has yet been found, but it has not been proven that none exists. See integer factorization
for a discussion of this problem.
Rivest, Shamir and Adleman note that Miller has shown that - assuming the Extended Riemann Hypothesis
(though others call it the Generalized Riemann Hypothesis
) - finding d from n and e is as hard as factoring n into p and q (up to a polynomial time difference). However, this proof does not imply that inverting RSA is equally hard as factoring.
, the largest (known) number factored by a general-purpose factoring
algorithm was 768 bits long (see RSA-768), using a state-of-the-art distributed implementation. RSA keys are typically 1024–2048 bits long. Some experts believe that 1024-bit keys may become breakable in the near future (though this is disputed); few see any way that 4096-bit keys could be broken in the foreseeable future. Therefore, it is generally presumed that RSA is secure if
is sufficiently large. If 
is 300 bit
s or shorter, it can be factored in a few hours on a personal computer
, using software already freely available. Keys of 512 bits have been shown to be practically breakable in 1999 when RSA-155 was factored by using several hundred computers and are now factored in a few weeks using common hardware. Exploits using 512-bit code-signing certificates that may have been factored were reported in 2011. A theoretical hardware device named TWIRL
and described by Shamir and Tromer in 2003 called into question the security of 1024 bit keys. It is currently recommended that
be at least 2048 bits long.
In 1994, Peter Shor
showed that a quantum computer
(if one could ever be practically created for the purpose) would be able to factor in polynomial time, breaking RSA.
s which quickly eliminate virtually all non-primes.
Numbers p and q should not be 'too close', lest the Fermat factorization for n be successful, if p − q, for instance is less than 2n1/4 (which for even small 1024-bit values of n is 3×1077) solving for p and q is trivial. Furthermore, if either p − 1 or q − 1 has only small prime factors, n can be factored quickly by Pollard's p − 1 algorithm, and these values of p or q should therefore be discarded as well.
It is important that the private key d be large enough. Michael J. Wiener showed that if p is between q and 2q (which is quite typical) and d < n1/4/3, then d can be computed efficiently from n and e.
There is no known attack against small public exponents such as e = 3, provided that proper padding is used. However, when no padding is used, or when the padding is improperly implemented, small public exponents have a greater risk of leading to an attack, such as the unpadded plaintext vulnerability listed above. 65537 is a commonly used value for e. This value can be regarded as a compromise between avoiding potential small exponent attacks and still allowing efficient encryptions (or signature verification). The NIST Special Publication on Computer Security (SP 800-78 Rev 1 of August 2007) does not allow public exponents e smaller than 65537, but does not state a reason for this restriction.
This procedure raises additional security issues. For instance, it is of utmost importance to use a strong random number generator for the symmetric key, because otherwise Eve (an eavesdropper wanting to see what was sent) could bypass RSA by guessing the symmetric key.
described a new attack on RSA in 1995: if the attacker Eve knows Alice's hardware in sufficient detail and is able to measure the decryption times for several known ciphertexts, she can deduce the decryption key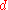
quickly. This attack can also be applied against the RSA signature scheme. In 2003, Boneh
and Brumley
demonstrated a more practical attack capable of recovering RSA factorizations over a network connection (e.g., from a Secure Socket Layer (SSL)-enabled webserver). This attack takes advantage of information leaked by the Chinese remainder theorem
optimization used by many RSA implementations.
One way to thwart these attacks is to ensure that the decryption operation takes a constant amount of time for every ciphertext. However, this approach can significantly reduce performance. Instead, most RSA implementations use an alternate technique known as cryptographic blinding
. RSA blinding makes use of the multiplicative property of RSA. Instead of computing
, Alice first chooses a secret random value 
and computes 
. The result of this computation after applying Euler's Theorem is 
and so the effect of 
can be removed by multiplying by its inverse. A new value of 
is chosen for each ciphertext. With blinding applied, the decryption time is no longer correlated to the value of the input ciphertext and so the timing attack fails.
described the first practical adaptive chosen ciphertext attack, against RSA-encrypted messages using the PKCS #1 v1 padding scheme
(a padding scheme randomizes and adds structure to an RSA-encrypted message, so it is possible to determine whether a decrypted message is valid.) Due to flaws with the PKCS #1 scheme, Bleichenbacher was able to mount a practical attack against RSA implementations of the Secure Socket Layer protocol, and to recover session keys. As a result of this work, cryptographers now recommend the use of provably secure padding schemes such as Optimal Asymmetric Encryption Padding
, and RSA Laboratories has released new versions of PKCS #1 that are not vulnerable to these attacks.
to determine whether a conditional branch in the instruction flow of a program is likely to be taken or not. Often these processors also implement simultaneous multithreading
(SMT). Branch prediction analysis attacks use a spy process to discover (statistically) the private key when processed with these processors.
Simple Branch Prediction Analysis (SBPA) claims to improve BPA in a non-statistical way. In their paper, "On the Power of Simple Branch Prediction Analysis", the authors of SBPA (Onur Aciicmez and Cetin Kaya Koc) claim to have discovered 508 out of 512 bits of an RSA key in 10 iterations.
A power fault attack on RSA implementations has been described in 2010. The authors recovered the key by varying the CPU power voltage outside limits; this caused multiple power faults on the server.
i.e.
Now, since
,
The last congruence directly follows from Euler's theorem when
is relatively prime to 
. In other case, it follows from the Chinese remainder theorem
.
. This theorem states that if p is prime and p does not divide a then
In RSA, the modulus
is a product of two primes p and q. The public key e and private key d satisfy
Therefore, there exists an integer h, such that
We can then continue to calculate
And likewise for q
If p and q are coprime,
and 
then the Chinese remainder theorem
implies
.
Hence
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for public-key cryptography
Public-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
that is based on the presumed difficulty of factoring large integers, the factoring problem. RSA stands for Ron Rivest
Ron Rivest
Ronald Linn Rivest is a cryptographer. He is the Andrew and Erna Viterbi Professor of Computer Science at MIT's Department of Electrical Engineering and Computer Science and a member of MIT's Computer Science and Artificial Intelligence Laboratory...
, Adi Shamir
Adi Shamir
Adi Shamir is an Israeli cryptographer. He is a co-inventor of the RSA algorithm , a co-inventor of the Feige–Fiat–Shamir identification scheme , one of the inventors of differential cryptanalysis and has made numerous contributions to the fields of cryptography and computer...
and Leonard Adleman
Leonard Adleman
Leonard Max Adleman is an American theoretical computer scientist and professor of computer science and molecular biology at the University of Southern California. He is known for being a co-inventor of the RSA cryptosystem in 1977, and of DNA computing...
, who first publicly described it in 1978. A user of RSA creates and then publishes the product of two large prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s, along with an auxiliary value, as their public key. The prime factors must be kept secret. Anyone can use the public key to encrypt a message, but with currently published methods, if the public key is large enough, only someone with knowledge of the prime factors can feasibly decode the message.
Whether breaking RSA encryption is as hard as factoring is an open question known as the RSA problem
RSA problem
In cryptography, the RSA problem summarizes the task of performing an RSA private-key operation given only the public key. The RSA algorithm raises a message to an exponent, modulo a composite number N whose factors are not known. As such, the task can be neatly described as finding the eth roots...
.
History
Clifford CocksClifford Cocks
Clifford Christopher Cocks, CB, is a British mathematician and cryptographer at GCHQ.He invented the widely-used encryption algorithm now commonly known as RSA, about three years before it was independently developed by Rivest, Shamir, and Adleman at MIT...
, an English mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
working for the UK
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
intelligence agency GCHQ
Government Communications Headquarters
The Government Communications Headquarters is a British intelligence agency responsible for providing signals intelligence and information assurance to the UK government and armed forces...
, described an equivalent system in an internal document in 1973, but given the relatively expensive computers needed to implement it at the time, it was mostly considered a curiosity and, as far as is publicly known, was never deployed. His discovery, however, was not revealed until 1998 due to its top-secret classification, and Rivest, Shamir, and Adleman devised RSA independently of Cocks' work.
The RSA algorithm was publicly described in 1978 by Ron Rivest
Ron Rivest
Ronald Linn Rivest is a cryptographer. He is the Andrew and Erna Viterbi Professor of Computer Science at MIT's Department of Electrical Engineering and Computer Science and a member of MIT's Computer Science and Artificial Intelligence Laboratory...
, Adi Shamir
Adi Shamir
Adi Shamir is an Israeli cryptographer. He is a co-inventor of the RSA algorithm , a co-inventor of the Feige–Fiat–Shamir identification scheme , one of the inventors of differential cryptanalysis and has made numerous contributions to the fields of cryptography and computer...
, and Leonard Adleman
Leonard Adleman
Leonard Max Adleman is an American theoretical computer scientist and professor of computer science and molecular biology at the University of Southern California. He is known for being a co-inventor of the RSA cryptosystem in 1977, and of DNA computing...
at MIT
Massachusetts Institute of Technology
The Massachusetts Institute of Technology is a private research university located in Cambridge, Massachusetts. MIT has five schools and one college, containing a total of 32 academic departments, with a strong emphasis on scientific and technological education and research.Founded in 1861 in...
; the letters RSA are the initials of their surnames, listed in the same order as on the paper.
MIT
Massachusetts Institute of Technology
The Massachusetts Institute of Technology is a private research university located in Cambridge, Massachusetts. MIT has five schools and one college, containing a total of 32 academic departments, with a strong emphasis on scientific and technological education and research.Founded in 1861 in...
was granted for a "Cryptographic communications system and method" that used the algorithm in 1983. The patent would have expired on September 21, 2000 (the term of patent
Term of patent
The term of a patent is the maximum period during which it can be maintained into force. It is usually expressed in number of years either starting from the filing date of the patent application or from the date of grant of the patent. In most patent laws, renewal annuities or maintenance fees have...
was 17 years at the time), but the algorithm was released to the public domain by RSA Security
RSA Security
RSA, the security division of EMC Corporation, is headquartered in Bedford, Massachusetts, United States, and maintains offices in Australia, Ireland, Israel, the United Kingdom, Singapore, India, China, Hong Kong and Japan....
on 6 September 2000, two weeks earlier. Since a paper describing the algorithm had been published in August 1977, prior to the December 1977 filing date of the patent application
Patent application
A patent application is a request pending at a patent office for the grant of a patent for the invention described and claimed by that application. An application consists of a description of the invention , together with official forms and correspondence relating to the application...
, regulations in much of the rest of the world precluded patent
Patent
A patent is a form of intellectual property. It consists of a set of exclusive rights granted by a sovereign state to an inventor or their assignee for a limited period of time in exchange for the public disclosure of an invention....
s elsewhere and only the US
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
patent was granted. Had Cocks' work been publicly known, a patent in the US might not have been possible.
From the DWPI's abstract of the patent,
The system includes a communications channel coupled to at least one terminal having an encoding device and to at least one terminal having a decoding device. A message-to-be-transferred is enciphered to ciphertext at the encoding terminal by encoding the message as a number M in a predetermined set. That number is then raised to a first predetermined power (associated with the intended receiver) and finally computed. The remainder or residue, C, is... computed when the exponentiated number is divided by the product of two predetermined prime numbers (associated with the intended receiver).
Operation
The RSA algorithm involves three steps: keyKey (cryptography)
In cryptography, a key is a piece of information that determines the functional output of a cryptographic algorithm or cipher. Without a key, the algorithm would produce no useful result. In encryption, a key specifies the particular transformation of plaintext into ciphertext, or vice versa...
generation, encryption and decryption.
Key generation
RSA involves a public key and a private key. The public key can be known to everyone and is used for encrypting messages. Messages encrypted with the public key can only be decrypted using the private key. The keys for the RSA algorithm are generated the following way:- Choose two distinct prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s p and q.- For security purposes, the integers p and q should be chosen at random, and should be of similar bit-length. Prime integers can be efficiently found using a primality testPrimality testA primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
.
- For security purposes, the integers p and q should be chosen at random, and should be of similar bit-length. Prime integers can be efficiently found using a primality test
- Compute
- n is used as the modulusModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
for both the public and private keys
- n is used as the modulus
- Compute , where φ is Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
. - Choose an integer e such that and , i.e. e and φ(n) are coprimeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
.- e is released as the public key exponent.
- e having a short bit-lengthBit-lengthThe length, in integers, of a binary number. The term "bit" is an abbreviation of "binary digits."At their most fundamental level, digital computers and telecommunications devices can process only data that has been expressed in binary format...
and small Hamming weightHamming weightThe Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
results in more efficient encryption - most commonly 0x10001 = 65537. However, small values of e (such as 3) have been shown to be less secure in some settings.
- Determine ; i.e. d is the multiplicative inverse of .
- This is more clearly stated as solve for d given (d*e)mod φ(n) = 1
- This is often computed using the extended Euclidean algorithmExtended Euclidean algorithmThe extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
. - d is kept as the private key exponent.
The public key consists of the modulus n and the public (or encryption) exponent e. The private key consists of the modulus n and the private (or decryption) exponent d which must be kept secret.
Notes:
- An alternative, used by PKCS#1PKCS1In cryptography, PKCS#1 is the first of a family of standards called Public-Key Cryptography Standards , published by RSA Laboratories. It provides the basic definitions of and recommendations for implementing the RSA algorithm for public-key cryptography...
, is to choose d matching with , where lcm is the least common multipleLeast common multipleIn arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
. Using λ instead of φ(n) allows more choices for d. λ can also be defined using the Carmichael function, λ(n). - The ANSI X9.31 standard prescribes, IEEE 1363 describes, and PKCS#1PKCS1In cryptography, PKCS#1 is the first of a family of standards called Public-Key Cryptography Standards , published by RSA Laboratories. It provides the basic definitions of and recommendations for implementing the RSA algorithm for public-key cryptography...
allows, that p and q match additional requirements: be strong primeStrong primeIn mathematics, a strong prime is a prime number with certain special properties. The definitions of strong primes are different in cryptography and number theory.- Definition in cryptography :...
s, and be different enough that Fermat factorization fails.
Encryption
AliceAlice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
transmits her public key
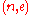to BobAlice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
and keeps the private key secret. Bob then wishes to send message M to Alice.
He first turns M into an integer m, such that
by using an agreed-upon reversible protocol known as a padding scheme. He then computes the ciphertext corresponding to-
.
This can be done quickly using the method of exponentiation by squaring
Exponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
. Bob then transmits
to Alice.Note that at least nine values of m will yield a ciphertext c equal to
m,
But this is very unlikely to occur in practice.
Decryption
Alice can recover from by using her private key exponent 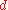via computing-
.
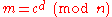Given
, she can recover the original message M by reversing the padding scheme.(In practice, there are more efficient methods of calculating
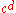using the pre computed values below.)Using the Chinese remainder algorithm
For efficiency many popular crypto libraries (like OpenSSL, Java and .NET) use the following optimization for decryption and signing:The following values are precomputed and stored as part of the private key:
-
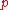and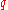 
: the primes from the key generation, -
, -
and -
.
These values allow the recipient to compute the exponentiation
more efficiently as follows:
-
-
-
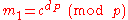
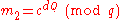
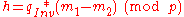(if 
then some libraries compute h as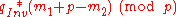 
) -
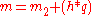
This is more efficient than computing
even though two modular exponentiations have to be computed.The reason is that these two modular exponentiations both use a smaller exponent and a smaller modulus.
A working example
Here is an example of RSA encryption and decryption. The parameters used here are artificially small, but one can also use OpenSSL to generate and examine a real keypair.- Choose two distinct prime numbers, such as
and 
.
- Compute
giving
- n = 61 · 53 = 3233.
- Compute the totient of the product as
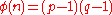giving
.
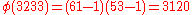- Choose any number
that is coprimeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to 3120. Choosing a prime number for
leaves us only to check that 
is not a divisor of 3120.
- Let
.
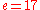- Let
- Compute
, the modular multiplicative inverse of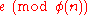 
yielding
.
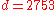The public key is (
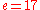, ). For a padded plaintextPlaintext
In cryptography, plaintext is information a sender wishes to transmit to a receiver. Cleartext is often used as a synonym. Before the computer era, plaintext most commonly meant message text in the language of the communicating parties....
message
, the encryption function is .The private key is (
, ). For an encrypted ciphertextCiphertext
In cryptography, ciphertext is the result of encryption performed on plaintext using an algorithm, called a cipher. Ciphertext is also known as encrypted or encoded information because it contains a form of the original plaintext that is unreadable by a human or computer without the proper cipher...
, the decryption function is .For instance, in order to encrypt
, we calculate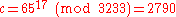.To decrypt
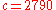, we calculate.Both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation
Modular exponentiation
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
. In real life situations the primes selected would be much larger; in our example it would be relatively trivial to factor
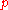, 3233, obtained from the freely available public key back to the primes and 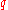. Given , also from the public key, we could then compute 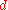and so acquire the private key.Practical implementations use Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
to speed up the calculation using modulus of factors (mod p*q using mod p and mod q).
The values dp, dq and qInv, which are part of the private key are computed as follows:
-
-
-
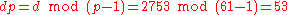
(Hence: 
)
Here is how dp, dq and qInv are used for efficient decryption. (Encryption is efficient by choice of public exponent e)
-
-
-
-
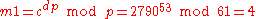
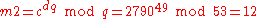
(same as above but computed more efficiently)
Attacks against plain RSA
There are a number of attacks against plain RSA as described below.- When encrypting with low encryption exponents (e.g.,
) and small values of the 
, (i.e. 
) the result of 
is strictly less than the modulus 
. In this case, ciphertexts can be easily decrypted by taking the 
th root of the ciphertext over the integers. - If the same clear text message is sent to
or more recipients in an encrypted way, and the receivers share the same exponent 
, but different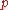 
, 
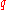, and therefore 
, then it is easy to decrypt the original clear text message via the Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
. Johan HåstadJohan HåstadJohan Torkel Håstad is a Swedish theoretical computer scientist most known for his work on computational complexity theory. He was the recipient of the Gödel Prize in 1994 and 2011 and the ACM Doctoral Dissertation Award in 1986, among other prizes...
noticed that this attack is possible even if the cleartexts are not equal, but the attacker knows a linear relation between them. This attack was later improved by Don CoppersmithDon CoppersmithDon Coppersmith is a cryptographer and mathematician. He was involved in the design of the Data Encryption Standard block cipher at IBM, particularly the design of the S-boxes, strengthening them against differential cryptanalysis...
.
- Because RSA encryption is a deterministic encryption algorithmDeterministic algorithmIn computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
– i.e., has no random component – an attacker can successfully launch a chosen plaintext attack against the cryptosystem, by encrypting likely plaintexts under the public key and test if they are equal to the ciphertext. A cryptosystem is called semantically secure if an attacker cannot distinguish two encryptions from each other even if the attacker knows (or has chosen) the corresponding plaintexts. As described above, RSA without padding is not semantically secure. - RSA has the property that the product of two ciphertexts is equal to the encryption of the product of the respective plaintexts. That is
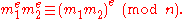Because of this multiplicative property a chosen-ciphertext attackChosen-ciphertext attackA chosen-ciphertext attack is an attack model for cryptanalysis in which the cryptanalyst gathers information, at least in part, by choosing a ciphertext and obtaining its decryption under an unknown key. In the attack, an adversary has a chance to enter one or more known ciphertexts into the...
is possible. E.g. an attacker, who wants to know the decryption of a ciphertext
may ask the holder of the private key to decrypt an unsuspicious-looking ciphertext 
for some value 
chosen by the attacker. Because of the multiplicative property 
is the encryption of 
. Hence, if the attacker is successful with the attack, he will learn 
from which he can derive the message m by multiplying 
with the modular inverse of 
modulo 
.
Padding schemes
To avoid these problems, practical RSA implementations typically embed some form of structured, randomized paddingPadding (cryptography)
-Classical cryptography:Official messages often start and end in predictable ways: My dear ambassador, Weather report, Sincerely yours, etc. The primary use of padding with classical ciphers is to prevent the cryptanalyst from using that predictability to find cribs that aid in breaking the...
into the value
before encrypting it. This padding ensures that does not fall into the range of insecure plaintexts, and that a given message, once padded, will encrypt to one of a large number of different possible ciphertexts.Standards such as PKCS#1
PKCS1
In cryptography, PKCS#1 is the first of a family of standards called Public-Key Cryptography Standards , published by RSA Laboratories. It provides the basic definitions of and recommendations for implementing the RSA algorithm for public-key cryptography...
have been carefully designed to securely pad messages prior to RSA encryption. Because these schemes pad the plaintext
with some number of additional bits, the size of the un-padded message M must be somewhat smaller. RSA padding schemes must be carefully designed so as to prevent sophisticated attacks which may be facilitated by a predictable message structure. Early versions of the PKCS#1 standard (up to version 1.5) used a construction that turned RSA into a semantically secure encryption scheme. This version was later found vulnerable to a practical adaptive chosen ciphertext attack. Later versions of the standard include Optimal Asymmetric Encryption PaddingOptimal Asymmetric Encryption Padding
In cryptography, Optimal Asymmetric Encryption Padding is a padding scheme often used together with RSA encryption. OAEP was introduced by Bellare and Rogaway....
(OAEP), which prevents these attacks. The PKCS#1 standard also incorporates processing schemes designed to provide additional security for RSA signatures, e.g., the Probabilistic Signature Scheme for RSA (RSA-PSS).
Signing messages
Suppose AliceAlice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
uses Bob
Alice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
's public key to send him an encrypted message. In the message, she can claim to be Alice but Bob has no way of verifying that the message was actually from Alice since anyone can use Bob's public key to send him encrypted messages. In order to verify the origin of a message, RSA can also be used to sign
Digital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
a message.
Suppose Alice wishes to send a signed message to Bob. She can use her own private key to do so. She produces a hash value
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
of the message, raises it to the power of
(as she does when decrypting a message), and attaches it as a "signature" to the message. When Bob receives the signed message, he uses the same hash algorithm in conjunction with Alice's public key. He raises the signature to the power of (as he does when encrypting a message), and compares the resulting hash value with the message's actual hash value. If the two agree, he knows that the author of the message was in possession of Alice's private key, and that the message has not been tampered with since.Secure padding schemes such as RSA-PSS are as essential for the security of message signing as they are for message encryption. The same key should never be used for both encryption and signing.
Integer factorization and RSA problem
The security of the RSA cryptosystem is based on two mathematical problems: the problem of factoring large numbersInteger factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
and the RSA problem
RSA problem
In cryptography, the RSA problem summarizes the task of performing an RSA private-key operation given only the public key. The RSA algorithm raises a message to an exponent, modulo a composite number N whose factors are not known. As such, the task can be neatly described as finding the eth roots...
. Full decryption of an RSA ciphertext is thought to be infeasible on the assumption that both of these problems are hard, i.e., no efficient algorithm exists for solving them. Providing security against partial decryption may require the addition of a secure padding scheme
Padding (cryptography)
-Classical cryptography:Official messages often start and end in predictable ways: My dear ambassador, Weather report, Sincerely yours, etc. The primary use of padding with classical ciphers is to prevent the cryptanalyst from using that predictability to find cribs that aid in breaking the...
.
The RSA problem
RSA problem
In cryptography, the RSA problem summarizes the task of performing an RSA private-key operation given only the public key. The RSA algorithm raises a message to an exponent, modulo a composite number N whose factors are not known. As such, the task can be neatly described as finding the eth roots...
is defined as the task of taking
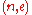th roots modulo a composite : recovering a value such that , where is an RSA public key and is an RSA ciphertext. Currently the most promising approach to solving the RSA problem is to factor the modulus . With the ability to recover prime factors, an attacker can compute the secret exponent from a public key , then decrypt using the standard procedure. To accomplish this, an attacker factors into and , and computes 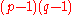which allows the determination of from . No polynomial-time method for factoring large integers on a classical computer has yet been found, but it has not been proven that none exists. See integer factorizationInteger factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
for a discussion of this problem.
Rivest, Shamir and Adleman note that Miller has shown that - assuming the Extended Riemann Hypothesis
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
(though others call it the Generalized Riemann Hypothesis
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
) - finding d from n and e is as hard as factoring n into p and q (up to a polynomial time difference). However, this proof does not imply that inverting RSA is equally hard as factoring.
, the largest (known) number factored by a general-purpose factoring
General number field sieve
In number theory, the general number field sieve is the most efficient classical algorithm known for factoring integers larger than 100 digits...
algorithm was 768 bits long (see RSA-768), using a state-of-the-art distributed implementation. RSA keys are typically 1024–2048 bits long. Some experts believe that 1024-bit keys may become breakable in the near future (though this is disputed); few see any way that 4096-bit keys could be broken in the foreseeable future. Therefore, it is generally presumed that RSA is secure if
is sufficiently large. If is 300 bitBit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s or shorter, it can be factored in a few hours on a personal computer
Personal computer
A personal computer is any general-purpose computer whose size, capabilities, and original sales price make it useful for individuals, and which is intended to be operated directly by an end-user with no intervening computer operator...
, using software already freely available. Keys of 512 bits have been shown to be practically breakable in 1999 when RSA-155 was factored by using several hundred computers and are now factored in a few weeks using common hardware. Exploits using 512-bit code-signing certificates that may have been factored were reported in 2011. A theoretical hardware device named TWIRL
TWIRL
In cryptography and number theory, TWIRL is a hypothetical hardware device designed to speed up the sieving step of the general number field sieve integer factorization algorithm. During the sieving step, the algorithm searches for numbers with a certain mathematical relationship...
and described by Shamir and Tromer in 2003 called into question the security of 1024 bit keys. It is currently recommended that
be at least 2048 bits long.In 1994, Peter Shor
Peter Shor
Peter Williston Shor is an American professor of applied mathematics at MIT, most famous for his work on quantum computation, in particular for devising Shor's algorithm, a quantum algorithm for factoring exponentially faster than the best currently-known algorithm running on a classical...
showed that a quantum computer
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
(if one could ever be practically created for the purpose) would be able to factor in polynomial time, breaking RSA.
Key generation
Finding the large primes p and q is usually done by testing random numbers of the right size with probabilistic primality testPrimality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
s which quickly eliminate virtually all non-primes.
Numbers p and q should not be 'too close', lest the Fermat factorization for n be successful, if p − q, for instance is less than 2n1/4 (which for even small 1024-bit values of n is 3×1077) solving for p and q is trivial. Furthermore, if either p − 1 or q − 1 has only small prime factors, n can be factored quickly by Pollard's p − 1 algorithm, and these values of p or q should therefore be discarded as well.
It is important that the private key d be large enough. Michael J. Wiener showed that if p is between q and 2q (which is quite typical) and d < n1/4/3, then d can be computed efficiently from n and e.
There is no known attack against small public exponents such as e = 3, provided that proper padding is used. However, when no padding is used, or when the padding is improperly implemented, small public exponents have a greater risk of leading to an attack, such as the unpadded plaintext vulnerability listed above. 65537 is a commonly used value for e. This value can be regarded as a compromise between avoiding potential small exponent attacks and still allowing efficient encryptions (or signature verification). The NIST Special Publication on Computer Security (SP 800-78 Rev 1 of August 2007) does not allow public exponents e smaller than 65537, but does not state a reason for this restriction.
This procedure raises additional security issues. For instance, it is of utmost importance to use a strong random number generator for the symmetric key, because otherwise Eve (an eavesdropper wanting to see what was sent) could bypass RSA by guessing the symmetric key.
Timing attacks
KocherPaul Kocher
Paul Carl Kocher is an American cryptographer and cryptography consultant, currently the president and chief scientist of Cryptography Research, Inc....
described a new attack on RSA in 1995: if the attacker Eve knows Alice's hardware in sufficient detail and is able to measure the decryption times for several known ciphertexts, she can deduce the decryption key
quickly. This attack can also be applied against the RSA signature scheme. In 2003, BonehDan Boneh
Dan Boneh is a Professor of Computer Science and Electrical Engineering atStanford University. He is a well-known researcher in the areas of applied cryptographyand computer security.-Education:...
and Brumley
David Brumley
David Brumley is an Assistant Professor at Carnegie Mellon University. He is a well-known researcher in software security, network security, and applied cryptography. Prof...
demonstrated a more practical attack capable of recovering RSA factorizations over a network connection (e.g., from a Secure Socket Layer (SSL)-enabled webserver). This attack takes advantage of information leaked by the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
optimization used by many RSA implementations.
One way to thwart these attacks is to ensure that the decryption operation takes a constant amount of time for every ciphertext. However, this approach can significantly reduce performance. Instead, most RSA implementations use an alternate technique known as cryptographic blinding
Blinding (cryptography)
In cryptography, blinding is a technique by which an agent can provide a service to a client in an encoded form without knowing either the real input or the real output. Blinding techniques also have applications to preventing side-channel attacks on encryption devices.More precisely, Alice has...
. RSA blinding makes use of the multiplicative property of RSA. Instead of computing
, Alice first chooses a secret random value and computes . The result of this computation after applying Euler's Theorem is and so the effect of can be removed by multiplying by its inverse. A new value of is chosen for each ciphertext. With blinding applied, the decryption time is no longer correlated to the value of the input ciphertext and so the timing attack fails.Adaptive chosen ciphertext attacks
In 1998, Daniel BleichenbacherDaniel Bleichenbacher
Daniel Bleichenbacher is a Swiss cryptographer, previously a researcher at Bell Labs, and currently employed at Google. He received his Ph.D...
described the first practical adaptive chosen ciphertext attack, against RSA-encrypted messages using the PKCS #1 v1 padding scheme
Padding (cryptography)
-Classical cryptography:Official messages often start and end in predictable ways: My dear ambassador, Weather report, Sincerely yours, etc. The primary use of padding with classical ciphers is to prevent the cryptanalyst from using that predictability to find cribs that aid in breaking the...
(a padding scheme randomizes and adds structure to an RSA-encrypted message, so it is possible to determine whether a decrypted message is valid.) Due to flaws with the PKCS #1 scheme, Bleichenbacher was able to mount a practical attack against RSA implementations of the Secure Socket Layer protocol, and to recover session keys. As a result of this work, cryptographers now recommend the use of provably secure padding schemes such as Optimal Asymmetric Encryption Padding
Optimal Asymmetric Encryption Padding
In cryptography, Optimal Asymmetric Encryption Padding is a padding scheme often used together with RSA encryption. OAEP was introduced by Bellare and Rogaway....
, and RSA Laboratories has released new versions of PKCS #1 that are not vulnerable to these attacks.
Side-channel analysis attacks
A side-channel attack using branch prediction analysis (BPA) has been described. Many processors use a branch predictorBranch predictor
In computer architecture, a branch predictor is a digital circuit that tries to guess which way a branch will go before this is known for sure. The purpose of the branch predictor is to improve the flow in the instruction pipeline...
to determine whether a conditional branch in the instruction flow of a program is likely to be taken or not. Often these processors also implement simultaneous multithreading
Simultaneous multithreading
Simultaneous multithreading, often abbreviated as SMT, is a technique for improving the overall efficiency of superscalar CPUs with hardware multithreading...
(SMT). Branch prediction analysis attacks use a spy process to discover (statistically) the private key when processed with these processors.
Simple Branch Prediction Analysis (SBPA) claims to improve BPA in a non-statistical way. In their paper, "On the Power of Simple Branch Prediction Analysis", the authors of SBPA (Onur Aciicmez and Cetin Kaya Koc) claim to have discovered 508 out of 512 bits of an RSA key in 10 iterations.
A power fault attack on RSA implementations has been described in 2010. The authors recovered the key by varying the CPU power voltage outside limits; this caused multiple power faults on the server.
Concise proof using Euler's Theorem
To show that a message encrypted with e can be decrypted with d we need to provei.e.
Now, since
,
The last congruence directly follows from Euler's theorem when
is relatively prime to . In other case, it follows from the Chinese remainder theoremChinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
.
Proof using Fermat's Little Theorem and Chinese Remainder Theorem
Another way to prove the correctness of RSA is based on Fermat's little theoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
. This theorem states that if p is prime and p does not divide a then
In RSA, the modulus
is a product of two primes p and q. The public key e and private key d satisfy
Therefore, there exists an integer h, such that
We can then continue to calculate
And likewise for q
If p and q are coprime,
and then the Chinese remainder theoremChinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
implies
.Hence
See also
- Public-key cryptographyPublic-key cryptographyPublic-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
- EncryptionEncryptionIn cryptography, encryption is the process of transforming information using an algorithm to make it unreadable to anyone except those possessing special knowledge, usually referred to as a key. The result of the process is encrypted information...
- Key exchangeKey exchangeKey exchange is any method in cryptography by which cryptographic keys are exchanged between users, allowing use of a cryptographic algorithm....
- Diffie-Hellman key exchangeDiffie-Hellman key exchangeDiffie–Hellman key exchange Synonyms of Diffie–Hellman key exchange include:*Diffie–Hellman key agreement*Diffie–Hellman key establishment*Diffie–Hellman key negotiation...
- Key managementKey managementKey management is the provisions made in a cryptography system design that are related to generation, exchange, storage, safeguarding, use, vetting, and replacement of keys. It includes cryptographic protocol design, key servers, user procedures, and other relevant protocols.Key management concerns...
- Cryptographic key length
- Computational complexity theoryComputational complexity theoryComputational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
External links
- The Original RSA Patent as filed with the U.S. Patent Office by Rivest; Ronald L. (Belmont, MA), Shamir; Adi (Cambridge, MA), Adleman; Leonard M. (Arlington, MA), December 14, 1977, .
- PKCS #1: RSA Cryptography Standard (RSA Laboratories website)
- The PKCSPKCSIn cryptography, PKCS refers to a group of public-key cryptography standards devised and published by RSA Security.RSA Data Security Inc was assigned the licensing rights for the patent on the RSA asymmetric key algorithm and acquired the licensing rights to several other key patents as well...
#1 standardStandardizationStandardization is the process of developing and implementing technical standards.The goals of standardization can be to help with independence of single suppliers , compatibility, interoperability, safety, repeatability, or quality....
"provides recommendations for the implementation of public-key cryptographyPublic-key cryptographyPublic-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
based on the RSA algorithm, covering the following aspects: cryptographic primitivesPrimitive typeIn computer science, primitive data type is either of the following:* a basic type is a data type provided by a programming language as a basic building block...
; encryptionEncryptionIn cryptography, encryption is the process of transforming information using an algorithm to make it unreadable to anyone except those possessing special knowledge, usually referred to as a key. The result of the process is encrypted information...
schemes; signatureDigital signatureA digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
schemes with appendix; ASN.1 syntax for representing keys and for identifying the schemes".
- The PKCS
- Thorough walk through of RSA
- Prime Number Hide-And-Seek: How the RSA Cipher Works
- Menezes, Oorschot, Vanstone, Scott: Handbook of Applied Cryptography (free PDF downloads), see Chapter 8
- Onur Aciicmez, Cetin Kaya Koc, Jean-Pierre Seifert: On the Power of Simple Branch Prediction Analysis
- A New Vulnerability In RSA Cryptography, CAcert NEWS Blog
- Example of an RSA implementation with PKCS#1 padding (GPL source code)
- Kocher's article about timing attacks
- Online RSA encryption application
- An animated explanation of RSA with its mathematical background by CrypTool