Riemann–Roch theorem
Encyclopedia
The Riemann–Roch theorem is an important tool in mathematics
, specifically in complex analysis
and algebraic geometry
, for the computation of the dimension of the space of meromorphic function
s with prescribed zeroes and allowed poles. It relates the complex analysis of a connected compact
Riemann surface
with the surface's purely topological genus
g, in a way that can be carried over into purely algebraic settings.
Initially proved as Riemann's inequality by , the theorem reached its definitive form for Riemann surfaces after work of Riemann
's short-lived student . It was later generalized to algebraic curve
s, to higher-dimensional varieties
and beyond.
s: functions with no poles
(i.e., constant functions), functions allowed at most a simple pole at P, functions allowed at most a double pole at P, a triple pole, ... These spaces are all finite dimensional. In case g = 0 we can see that the sequence of dimensions starts
this can be read off from the theory of partial fraction
s. Conversely if this sequence starts
then g must be zero (the so-called Riemann sphere
).
In the theory of elliptic function
s it is shown that for g = 1 this sequence is
and this characterises the case g = 1. For g > 2 there is no set initial segment; but it is possible to say what the tail of the sequence must be. It is also possible to explain why the case g = 2 is somewhat special, by means of the theory of hyperelliptic curves, namely those with the sequence starting 1, 1, 2, ... .
The reason that the results take the form they do goes back to the formulation (Roch's part) of the theorem: as a difference of two such dimensions. When one of those can be set to zero, we get an exact formula, which is linear in the genus and the degree (i.e. number of degrees of freedom). Already the examples given allow a reconstruction in the shape
For g = 1 the correction is 1 for degree 0; and otherwise 0. The full theorem explains the correction as the dimension associated to a further, 'complementary' space of functions.
This applies to all divisors D, elements of the free abelian group
on the points of the surface. Equivalently, a divisor is a finite linear combination of points of the surface with integer coefficients.
We define the divisor of a meromorphic function f as
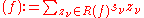
where R(f) is the set of all zeroes and poles of f, and sν is given by
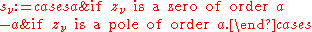
We define the divisor of a meromorphic 1-form similarly. A divisor of a global meromorphic function is called a principal divisor. Two divisors that differ by a principal divisor are called linearly equivalent. A divisor of a global meromorphic 1-form is called the canonical divisor (usually denoted K). Any two meromorphic 1-forms will yield linearly equivalent divisors, so the canonical divisor is uniquely determined up to linear equivalence (hence "the" canonical divisor).
The symbol deg(D) denotes the degree of the divisor D, i.e. the sum of the coefficients occurring in D. It can be shown that the divisor of a global meromorphic function always has degree 0, so the degree of the divisor depends only on the linear equivalence class.
The number l(D) is the quantity that is of primary interest: the dimension
(over C
) of the vector space of meromorphic functions h on the surface, such that all the coefficients of (h) + D are non-negative. Intuitively, we can think of this as being all meromorphic functions whose poles at every point are no worse than the corresponding coefficient in D; if the coefficient in D at z is negative, then we require that h has a zero of at least that multiplicity at z – if the coefficient in D is positive, h can have a pole of at most that order. The vector spaces for linearly equivalent divisors are naturally isomorphic through multiplication with the global meromorphic function (which is well-defined up to a scalar).
Even if we don't know anything about K, we know at least that the index of speciality (the "correction" referred to above) is non-negative, so that
and therefore
which is Riemann's inequality mentioned earlier.
The theorem above is correct for all compact connected Riemann surfaces. The formula also holds for all non-singular projective algebraic curves over an algebraically closed field
k. Here l(D) denotes the dimension (over k) of the space of rational function
s on the curve whose poles at every point are not worse than the corresponding coefficient in D.
To relate this to our example above, we need some information about K: for g = 1 we can take K = 0, while for g = 0 we can take K = −2P (any P). In general K has degree 2g − 2. As long as D has degree at least 2g − 1 we can be sure that the correction term is 0.
Going back therefore to the case g = 2 we see that the sequence mentioned above is
It is shown from this that the ? term of degree 2 is either 1 or 2, of course depending on the point. It can be proven that in any genus 2 curve there are exactly six points whose sequences are 1, 1, 2, 2, ... and the rest of the points have the generic sequence 1, 1, 1, 2, ... In particular, a genus 2 curve is a hyperelliptic curve. For g > 2 it is always true that at most points the sequence starts with g+1 ones and there are finitely many points with other sequences (see Weierstrass point
s).
Riemann surface
X of genus g and let
denote the space of holomorphic sections of L. This space will be finite-dimensional; its dimension is denoted 
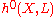. Let K denote the canonical bundle
on X. Then, the Riemann-Roch theorem states that
The theorem of the previous section is the special case of when L is a point bundle. The theorem can be applied to show that there are g holomorphic sections of K, or one-forms, on X. Taking L to be the trivial bundle,
since the only holomorphic functions on X are constants. The degree of L is zero, and L^{-1} is the trivial bundle. Thus,
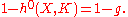
Therefore,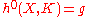
, proving that there are g holomorphic one-forms.
There are versions in higher dimensions (for the appropriate notion of divisor
, or line bundle
). Their general formulation depends on splitting the theorem into two parts. One, which would now be called Serre duality
, interprets the l(K − D) term as a dimension of a first sheaf cohomology
group; with l(D) the dimension of a zeroth cohomology group, or space of sections, the left-hand side of the theorem becomes an Euler characteristic
, and the right-hand side a computation of it as a degree corrected according to the topology of the Riemann surface.
In algebraic geometry
of dimension two such a formula was found by the geometers of the Italian school
; a Riemann–Roch theorem for algebraic surfaces was proved (there are several versions, with the first possibly being due to Max Noether
). So matters rested before about 1950.
An n-dimensional generalisation, the Hirzebruch–Riemann–Roch theorem, was found and proved by Friedrich Hirzebruch
, as an application of characteristic class
es in algebraic topology
; he was much influenced by the work of Kunihiko Kodaira. At about the same time Jean-Pierre Serre
was giving the general form of Serre duality, as we now know it.
Alexander Grothendieck
proved a far-reaching generalization in 1957, now known as the Grothendieck–Riemann–Roch theorem. His work reinterprets Riemann–Roch not as a theorem about a variety, but about a morphism between two varieties. The details of the proofs were published by Borel-Serre in 1958.
Finally a general version was found in algebraic topology
, too. These developments were essentially all carried out between 1950 and 1960. After that the Atiyah–Singer index theorem
opened another route to generalization.
What results is that the Euler characteristic (of a coherent sheaf
) is something reasonably computable. If one is interested, as is usually the case, in just one summand within the alternating sum, further arguments such as vanishing theorem
s must be brought to bear.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, for the computation of the dimension of the space of meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s with prescribed zeroes and allowed poles. It relates the complex analysis of a connected compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
with the surface's purely topological genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
g, in a way that can be carried over into purely algebraic settings.
Initially proved as Riemann's inequality by , the theorem reached its definitive form for Riemann surfaces after work of Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
's short-lived student . It was later generalized to algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s, to higher-dimensional varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
and beyond.
Motivation
We start with a connected compact Riemann surface of genus g, and a fixed point P on it. We may look at functions having a pole only at P. There is an increasing sequence of vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s: functions with no poles
(i.e., constant functions), functions allowed at most a simple pole at P, functions allowed at most a double pole at P, a triple pole, ... These spaces are all finite dimensional. In case g = 0 we can see that the sequence of dimensions starts
- 1, 2, 3, ...:
this can be read off from the theory of partial fraction
Partial fraction
In algebra, the partial fraction decomposition or partial fraction expansion is a procedure used to reduce the degree of either the numerator or the denominator of a rational function ....
s. Conversely if this sequence starts
- 1, 2, ...
then g must be zero (the so-called Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
).
In the theory of elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s it is shown that for g = 1 this sequence is
- 1, 1, 2, 3, 4, 5 ... ;
and this characterises the case g = 1. For g > 2 there is no set initial segment; but it is possible to say what the tail of the sequence must be. It is also possible to explain why the case g = 2 is somewhat special, by means of the theory of hyperelliptic curves, namely those with the sequence starting 1, 1, 2, ... .
The reason that the results take the form they do goes back to the formulation (Roch's part) of the theorem: as a difference of two such dimensions. When one of those can be set to zero, we get an exact formula, which is linear in the genus and the degree (i.e. number of degrees of freedom). Already the examples given allow a reconstruction in the shape
- dimension − correction = degree − g + 1.
For g = 1 the correction is 1 for degree 0; and otherwise 0. The full theorem explains the correction as the dimension associated to a further, 'complementary' space of functions.
Statement of the theorem
In now-accepted notation, the statement of Riemann–Roch for a compact Riemann surface of genus g with canonical divisor K is- l(D) − l(K − D) = deg(D) − g + 1.
This applies to all divisors D, elements of the free abelian group
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
on the points of the surface. Equivalently, a divisor is a finite linear combination of points of the surface with integer coefficients.
We define the divisor of a meromorphic function f as
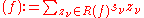
where R(f) is the set of all zeroes and poles of f, and sν is given by
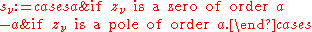
We define the divisor of a meromorphic 1-form similarly. A divisor of a global meromorphic function is called a principal divisor. Two divisors that differ by a principal divisor are called linearly equivalent. A divisor of a global meromorphic 1-form is called the canonical divisor (usually denoted K). Any two meromorphic 1-forms will yield linearly equivalent divisors, so the canonical divisor is uniquely determined up to linear equivalence (hence "the" canonical divisor).
The symbol deg(D) denotes the degree of the divisor D, i.e. the sum of the coefficients occurring in D. It can be shown that the divisor of a global meromorphic function always has degree 0, so the degree of the divisor depends only on the linear equivalence class.
The number l(D) is the quantity that is of primary interest: the dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
(over C
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
) of the vector space of meromorphic functions h on the surface, such that all the coefficients of (h) + D are non-negative. Intuitively, we can think of this as being all meromorphic functions whose poles at every point are no worse than the corresponding coefficient in D; if the coefficient in D at z is negative, then we require that h has a zero of at least that multiplicity at z – if the coefficient in D is positive, h can have a pole of at most that order. The vector spaces for linearly equivalent divisors are naturally isomorphic through multiplication with the global meromorphic function (which is well-defined up to a scalar).
Even if we don't know anything about K, we know at least that the index of speciality (the "correction" referred to above) is non-negative, so that
- l(K − D) ≥ 0,
and therefore
- l(D) ≥ deg(D) − g + 1
which is Riemann's inequality mentioned earlier.
The theorem above is correct for all compact connected Riemann surfaces. The formula also holds for all non-singular projective algebraic curves over an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
k. Here l(D) denotes the dimension (over k) of the space of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s on the curve whose poles at every point are not worse than the corresponding coefficient in D.
To relate this to our example above, we need some information about K: for g = 1 we can take K = 0, while for g = 0 we can take K = −2P (any P). In general K has degree 2g − 2. As long as D has degree at least 2g − 1 we can be sure that the correction term is 0.
Going back therefore to the case g = 2 we see that the sequence mentioned above is
- 1, 1, ?, 2, 3, ... .
It is shown from this that the ? term of degree 2 is either 1 or 2, of course depending on the point. It can be proven that in any genus 2 curve there are exactly six points whose sequences are 1, 1, 2, 2, ... and the rest of the points have the generic sequence 1, 1, 1, 2, ... In particular, a genus 2 curve is a hyperelliptic curve. For g > 2 it is always true that at most points the sequence starts with g+1 ones and there are finitely many points with other sequences (see Weierstrass point
Weierstrass point
In mathematics, a Weierstrass point P on a nonsingular algebraic curve C defined over the complex numbers is a point such that there are extra functions on C, with their poles restricted to P only, than would be predicted by looking at the Riemann–Roch theorem...
s).
Riemann-Roch for Line Bundles
Let L be a holomorphic line bundle on a compactCompact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:* Interstate compact* Compact government, a type of colonial rule utilized in British North America...
Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
X of genus g and let
denote the space of holomorphic sections of L. This space will be finite-dimensional; its dimension is denoted 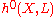. Let K denote the canonical bundleCanonical bundle
In mathematics, the canonical bundle of a non-singular algebraic variety V of dimension n is the line bundle\,\!\Omega^n = \omegawhich is the nth exterior power of the cotangent bundle Ω on V. Over the complex numbers, it is the determinant bundle of holomorphic n-forms on V.This is the dualising...
on X. Then, the Riemann-Roch theorem states that
The theorem of the previous section is the special case of when L is a point bundle. The theorem can be applied to show that there are g holomorphic sections of K, or one-forms, on X. Taking L to be the trivial bundle,
since the only holomorphic functions on X are constants. The degree of L is zero, and L^{-1} is the trivial bundle. Thus,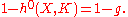Therefore,
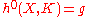, proving that there are g holomorphic one-forms.Generalizations of the Riemann-Roch Theorem
The Riemann–Roch theorem for curves was proved for Riemann surfaces by Riemann and Roch in the 1850s and for algebraic curves by F. K. Schmidt in 1929 (cf. the dedicated article Riemann-Roch theorem for algebraic curves). It is foundational in the sense that the subsequent theory for curves tries to refine the information it yields (for example in the Brill–Noether theory).There are versions in higher dimensions (for the appropriate notion of divisor
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
, or line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
). Their general formulation depends on splitting the theorem into two parts. One, which would now be called Serre duality
Serre duality
In algebraic geometry, a branch of mathematics, Serre duality is a duality present on non-singular projective algebraic varieties V of dimension n . It shows that a cohomology group Hi is the dual space of another one, Hn−i...
, interprets the l(K − D) term as a dimension of a first sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
group; with l(D) the dimension of a zeroth cohomology group, or space of sections, the left-hand side of the theorem becomes an Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
, and the right-hand side a computation of it as a degree corrected according to the topology of the Riemann surface.
In algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
of dimension two such a formula was found by the geometers of the Italian school
Italian school of algebraic geometry
In relation with the history of mathematics, the Italian school of algebraic geometry refers to the work over half a century or more done internationally in birational geometry, particularly on algebraic surfaces. There were in the region of 30 to 40 leading mathematicians who made major...
; a Riemann–Roch theorem for algebraic surfaces was proved (there are several versions, with the first possibly being due to Max Noether
Max Noether
Max Noether was a German mathematician who worked on algebraic geometry and the theory of algebraic functions. He has been called "one of the finest mathematicians of the nineteenth century".-Biography:...
). So matters rested before about 1950.
An n-dimensional generalisation, the Hirzebruch–Riemann–Roch theorem, was found and proved by Friedrich Hirzebruch
Friedrich Hirzebruch
Friedrich Ernst Peter Hirzebruch is a German mathematician, working in the fields of topology, complex manifolds and algebraic geometry, and a leading figure in his generation.-Life:He was born in Hamm, Westphalia...
, as an application of characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
; he was much influenced by the work of Kunihiko Kodaira. At about the same time Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
was giving the general form of Serre duality, as we now know it.
Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
proved a far-reaching generalization in 1957, now known as the Grothendieck–Riemann–Roch theorem. His work reinterprets Riemann–Roch not as a theorem about a variety, but about a morphism between two varieties. The details of the proofs were published by Borel-Serre in 1958.
Finally a general version was found in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, too. These developments were essentially all carried out between 1950 and 1960. After that the Atiyah–Singer index theorem
Atiyah–Singer index theorem
In differential geometry, the Atiyah–Singer index theorem, proved by , states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index...
opened another route to generalization.
What results is that the Euler characteristic (of a coherent sheaf
Coherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
) is something reasonably computable. If one is interested, as is usually the case, in just one summand within the alternating sum, further arguments such as vanishing theorem
Vanishing theorem
In algebraic geometry, a vanishing theorem gives conditions for coherent cohomology groups to vanish.*Grauert–Riemenschneider vanishing theorem*Kawamata–Viehweg vanishing theorem*Kollár vanishing theorem*Kodaira vanishing theorem*Miyaoka vanishing theorem...
s must be brought to bear.