Rng (algebra)
Encyclopedia
In abstract algebra
, a rng (also called a pseudo-ring or non-unital ring) is an algebraic structure
satisfying the same properties as a ring
, except that multiplication need not have an identity element
. The term "rng" is meant to suggest that it is a "ring" without an "identity element", i.
Many authors do not require rings to have a multiplicative identity, so the concept discussed here is just what these authors call a ring.
Homomorphism
s between rngs are defined just like ring homomorphism
s except that the requirement f(1) = 1 is dropped. That is, a rng homomorphism is a function f : R → S from one rng to another such that
for all x and y in R.
One can prove, however, that if a rng homomorphism f : R → S takes 1 to a unit s of S, then s = 1, or further that any rng homomorphism mapping any nonzero element to an element that is not a zero divisor in fact maps 1 to 1. Corollary : if a rng homomorphism maps a unit to a unit then it maps the identity of R to the identity of S.
whose bottom row is zero. Both of these examples are instances of the general fact that every (one- or two-sided) ideal
is a rng.
Any abelian group can be made into a rng by taking the multiplication operation to be trivial (i.e. r·s = 0 for all r and s): such rng is called a zero ring
. This rng will not have an identity unless it is trivial.
Rngs often appear naturally in functional analysis
when linear operators on infinite-dimensional vector space
s are considered. Take for instance any infinite-dimensional vector space V and consider the set of all linear operators f : V → V with finite rank
(i.e. dim f(V) < ∞). Together with addition and composition of operators, this is a rng, but not a ring. Another example is the rng of all real sequence
s that converge to
0, with component-wise operations.
Also, many test function spaces occurring in the theory of distributions consist of functions
decreasing to zero at infinity, like e.g. Schwartz space. Thus, the function everywhere equal to one, which would be the only possible identity element for pointwise multiplication, cannot exist in such spaces, which therefore are rngs (for pointwise addition and multiplication).
In particular, the real-valued continuous function
s with compact
support
defined on some topological space
, together with pointwise addition and multiplication, form a rng; this is not a ring unless the underlying space is compact
.
s can be defined for rngs in the same manner as for rings. The ideal theory of rngs is complicated by the fact that a rng, unlike a ring, need not contain any maximal ideal
s. Many theorems of ring theory
are false for rngs.
where n is an integer
and r ∈ R. Multiplication is defined by linearity:·(n2 + r2) = n1n2 + n1r2 + n2r1 + r1r2.
More formally, we can take R^ to be the cartesian product
Z × R and define addition and multiplication by + (n2, r2) = (n1 + n2, r1 + r2),·(n2, r2) = (n1n2, n1r2 + n2r1 + r1r2).
The multiplicative identity of R^ is then (1, 0). There is a natural rng homomorphism j : R → R^ defined by j(r) = (0, r). This map has the following universal property
:
The map g can be defined by g(n, r) = n·1S + f(r). In a sense then, R^ is "the most general" ring containing R.
There is a natural surjective ring homomorphism R^ → Z which sends (n, r) to n. The kernel of this homomorphism is the image of R in R^. Since j is injective, we see that R is embedded as a (two-sided) ideal
in R^ with the quotient ring
R^/R isomorphic to Z. It follows that
Note that j is never surjective. So even when R already has an identity element the ring R^ will be a larger one with a different identity.
The process of adjoining an identity element to a rng can be formulated in the language of category theory
. If we denote the category of all rings and ring homomorphisms by Ring and the category of all rngs and rng homomorphisms by Rng, then Ring is a (nonfull) subcategory
of Rng. The construction of R^ given above yields a left adjoint to the inclusion functor I : Ring → Rng. This means that Ring is a reflective subcategory
of Rng with reflector j : R → R^.
For example:
It is not hard to check that these properties are weaker than having an identity element and weaker than the previous one.
if the product of any two elements in R is the additive identity 0.
A zero rng that has a multiplicative identity (that is, which is a ring) must be the trivial rng. Therefore, the concept of a zero rng is interesting only for rngs that are not rings.
Any abelian group
can be turned into a zero ring by letting a · b = 0 for every a, b in the group (and letting + be the group operation of that abelian group).
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a rng (also called a pseudo-ring or non-unital ring) is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
satisfying the same properties as a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, except that multiplication need not have an identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. The term "rng" is meant to suggest that it is a "ring" without an "identity element", i.
Many authors do not require rings to have a multiplicative identity, so the concept discussed here is just what these authors call a ring.
Formal definition
Formally, a rng is a set R with two binary operations (+, ·) called addition and multiplication such that- (R, +) is an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, - (R, ·) is a semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
, - Multiplication distributes over addition.
Homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s between rngs are defined just like ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
s except that the requirement f(1) = 1 is dropped. That is, a rng homomorphism is a function f : R → S from one rng to another such that
- f(x + y) = f(x) + f(y)
- f(x·y) = f(x)·f(y)
for all x and y in R.
One can prove, however, that if a rng homomorphism f : R → S takes 1 to a unit s of S, then s = 1, or further that any rng homomorphism mapping any nonzero element to an element that is not a zero divisor in fact maps 1 to 1. Corollary : if a rng homomorphism maps a unit to a unit then it maps the identity of R to the identity of S.
Examples
Of course all rings are rngs. A simple example of a rng that is not a ring is given by the even integers with the ordinary addition and multiplication of integers. Another example is given by the set of all 3-by-3 real matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
whose bottom row is zero. Both of these examples are instances of the general fact that every (one- or two-sided) ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
is a rng.
Any abelian group can be made into a rng by taking the multiplication operation to be trivial (i.e. r·s = 0 for all r and s): such rng is called a zero ring
Zero ring
In ring theory, a branch of mathematics, a zero ring is a ring in which the product of any two elements is 0 . In ring theory, a branch of mathematics, a zero ring is a ring (without unity) in which the product of any two elements is 0 (the additive identity element). In ring theory, a branch of...
. This rng will not have an identity unless it is trivial.
Rngs often appear naturally in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
when linear operators on infinite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s are considered. Take for instance any infinite-dimensional vector space V and consider the set of all linear operators f : V → V with finite rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
(i.e. dim f(V) < ∞). Together with addition and composition of operators, this is a rng, but not a ring. Another example is the rng of all real sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s that converge to
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
0, with component-wise operations.
Also, many test function spaces occurring in the theory of distributions consist of functions
decreasing to zero at infinity, like e.g. Schwartz space. Thus, the function everywhere equal to one, which would be the only possible identity element for pointwise multiplication, cannot exist in such spaces, which therefore are rngs (for pointwise addition and multiplication).
In particular, the real-valued continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s with compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
defined on some topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, together with pointwise addition and multiplication, form a rng; this is not a ring unless the underlying space is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
.
Properties
Ideals and quotient ringQuotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
s can be defined for rngs in the same manner as for rings. The ideal theory of rngs is complicated by the fact that a rng, unlike a ring, need not contain any maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
s. Many theorems of ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
are false for rngs.
Adjoining an identity element
Every rng R can be turned into a ring R^ by adjoining an identity element. The most general way in which to do this is to formally add an identity element 1 and let R^ consist of integral linear combinations of 1 and elements of R. That is, elements of R^ are of the form- n·1 + r
where n is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
and r ∈ R. Multiplication is defined by linearity:·(n2 + r2) = n1n2 + n1r2 + n2r1 + r1r2.
More formally, we can take R^ to be the cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
Z × R and define addition and multiplication by + (n2, r2) = (n1 + n2, r1 + r2),·(n2, r2) = (n1n2, n1r2 + n2r1 + r1r2).
The multiplicative identity of R^ is then (1, 0). There is a natural rng homomorphism j : R → R^ defined by j(r) = (0, r). This map has the following universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
:
- Given any ring S and any rng homomorphism f : R → S, there exists a unique ring homomorphisms g : R^ → S such that f = gj.
The map g can be defined by g(n, r) = n·1S + f(r). In a sense then, R^ is "the most general" ring containing R.
There is a natural surjective ring homomorphism R^ → Z which sends (n, r) to n. The kernel of this homomorphism is the image of R in R^. Since j is injective, we see that R is embedded as a (two-sided) ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in R^ with the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
R^/R isomorphic to Z. It follows that
- Every rng is an ideal in some ring, and every ideal of a ring is a rng.
Note that j is never surjective. So even when R already has an identity element the ring R^ will be a larger one with a different identity.
The process of adjoining an identity element to a rng can be formulated in the language of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. If we denote the category of all rings and ring homomorphisms by Ring and the category of all rngs and rng homomorphisms by Rng, then Ring is a (nonfull) subcategory
Subcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and...
of Rng. The construction of R^ given above yields a left adjoint to the inclusion functor I : Ring → Rng. This means that Ring is a reflective subcategory
Reflective subcategory
In mathematics, a subcategory A of a category B is said to be reflective in B when the inclusion functor from A to B has a left adjoint. This adjoint is sometimes called a reflector...
of Rng with reflector j : R → R^.
Properties weaker than having an identity
There are several properties that have been considered in the literature that are weaker than having an identity element, but not so general.For example:
- Rings with enough idempotents: A rng R is said to be a ring with enough idempotents in case there exists a subset E of R given by idempotents (i.e. e2 = e for all e in E) orthogonal (i.e. ef = 0 for all e≠f in E) such that
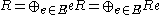. - Rings with local units: A rng R is said to be a ring with local units in case for every finite set r1, r2, ..., rt in R we can find e in R such that e2 = e and eri = ri = rie for every i
- s-unital rings: A rng R is said to be s-unital in case for every finite set r1, r2, ..., rt in R we can find s in R such that sri = ri = ris for every i.
- Firm rings: A rng R is said to be firm if the canonical homomorphism
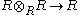given by 
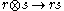is an isomorphism. - Idempotent rings: A rng R is said to be idempotent in case R2 = R, that is, for every element r of R we can find elements ri and si in R such that
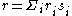
It is not hard to check that these properties are weaker than having an identity element and weaker than the previous one.
- Rings are rings with enough idempotents, using E = {1}. A ring with enough idempotents that has no identity is for example the ring of infinite matrices over a field with just a finite number of nonzero entries. The matrices that have just 1 over one element in the main diagonal and 0 otherwise are the orthogonal idempotents.
- Rings with enough idempotents are rings with local units just taking finite sums of the orthogonal idempotents to satisfy the definition.
- Rings with local units are in particular s-unital, s-unital rings are firm and firm rings are idempotent.
Zero rng
A rng (R, +, · ) is said to be a zero rngZero ring
In ring theory, a branch of mathematics, a zero ring is a ring in which the product of any two elements is 0 . In ring theory, a branch of mathematics, a zero ring is a ring (without unity) in which the product of any two elements is 0 (the additive identity element). In ring theory, a branch of...
if the product of any two elements in R is the additive identity 0.
A zero rng that has a multiplicative identity (that is, which is a ring) must be the trivial rng. Therefore, the concept of a zero rng is interesting only for rngs that are not rings.
Any abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
can be turned into a zero ring by letting a · b = 0 for every a, b in the group (and letting + be the group operation of that abelian group).