Rook's graph
Encyclopedia
In graph theory
, a rook's graph is a graph that represents all legal moves of the rook
chess
piece
on a chessboard
: each vertex represents a square on a chessboard and each edge represents a legal move. Rook's graphs are highly symmetric perfect graph
s; they may be characterized in terms of the number of triangles each edge belongs to and by the existence of a 4-cycle connecting each nonadjacent pair of vertices.
Its vertices may be given coordinates (x,y), where 1 ≤ x ≤ n and 1 ≤ y ≤ m. Two vertices (x1,y1) and (x2,y2) are adjacent if and only if either x1 = x2 or y1 = y2; that is, if they belong to the same rank or the same file of the chessboard.
For an n × m rook's graph the total number of vertices is simply nm. For an n × n rook's graph the total number of vertices is simply
and the total number of edges is 
; in this case the graph is also known as a two-dimensional Hamming graph or a Latin square
graph.
The rook's graph for an n × m chessboard may also be defined as the Cartesian product
of two complete graph
s Kn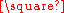
Km. The complement graph
of a 2 × n rook's graph is a crown graph
.
and (n + m − 2)-regular
; they are the only regular graphs formed from the moves of standard chess pieces in this way (Elkies). When m ≠ n, the symmetries of the rook's graph are formed by independently permuting the rows and columns of the graph. When n = m the graph has additional symmetries that swap the rows and columns; the rook's graph for a square chessboard is symmetric.
Any two vertices in a rook's graph are either at distance one or two from each other, according to whether they are adjacent or nonadjacent respectively. Any two nonadjacent vertices may be transformed into any other two nonadjacent vertices by a symmetry of the graph. When the rook's graph is not square, the pairs of adjacent vertices fall into two orbits of the symmetry group according to whether they are adjacent horizontally or vertically, but when the graph is square any two adjacent vertices may also be mapped into each other by a symmetry and the graph is therefore distance-transitive
.
When m and n are relatively prime, the symmetry group Sm×Sn of the rook's graph contains as a subgroup the cyclic group
Cmn = Cm×Cn that acts
by cyclically permuting the mn vertices; therefore, in this case, the rook's graph is a circulant graph
.
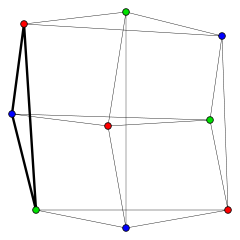A rook's graph can also be viewed as the line graph
of a complete bipartite graph
Kn,m — that is, it has one vertex for each edge of Kn,m, and two vertices of the rook's graph are adjacent if and only if the corresponding edges of the complete bipartite graph share a common endpoint. In this view, an edge in the complete bipartite graph from the ith vertex on one side of the bipartition to the jth vertex on the other side corresponds to a chessboard square with coordinates (i,j).
Any bipartite graph
is a subgraph of a complete bipartite graph, and correspondingly any line graph of a bipartite graph is an induced subgraph of a rook's graph. The line graphs of bipartite graphs are perfect
: in them, and in any of their induced subgraphs, the number of colors needed in any vertex coloring
is the same as the number of vertices in the largest complete subgraph
. Line graphs of bipartite graphs form an important family of perfect graphs: they are one of a small number of families used by to characterize the perfect graphs and to show that every graph with no odd hole and no odd antihole is perfect. In particular, rook's graphs are themselves perfect.
Because a rook's graph is perfect, the number of colors needed in any coloring of the graph is just the size of its largest clique. The cliques of a rook's graph are the subsets of its rows and columns, and the largest of these have size max(m,n), so this is also the chromatic number of the graph. An n-coloring of an n×n rook's graph may be interpreted as a Latin square
: it describes a way of filling the rows and columns of an n×n grid with n different values in such a way that the same value does not appear twice in any row or column.
An independent set
in a rook's graph is a set of vertices, no two of which belong to the same row or column of the graph. Perfect graphs may also be described as the graphs in which, in every induced subgraph, the size of the largest independent set is equal to the number of cliques in a partition of the graph's vertices into a minimum number of cliques. In a rook's graph, the sets of rows or the sets of columns (whichever has fewer sets) form such an optimal partition. The size of the largest independent set in the graph is therefore min(m,n). Every color class in every optimal coloring of a rook's graph is a maximum independent set.
When n = m, these conditions may be abbreviated by stating that an n×n rook's graph is a strongly regular graph
with parameters
srg(n2, 2n − 2, n − 2, 2), and that every strongly regular graph with these parameters must be an n×n rook's graph when n≠4. When n=4, there is another strongly regular graph, the Shrikhande graph
, with the same parameters as the 4×4 rook's graph.
The Shrikhande graph can be distinguished from the 4×4 rook's graph in that the neighborhood of any vertex in the Shrikhande graph is connected in a 6-cycle, while in the rook's graph it is connected into two triangles.
On the rook's graph a k-dominating set is a set of vertices whose corresponding squares attack all other squares (via a rook's move) at least k times. A k-tuple dominating set on the rook's graph is a set of vertices whose corresponding squares attack all other squares at least k times and are themselves attacked at least k − 1 times. The minimum cardinality among all k-dominating and k-tuple dominating sets are the k-domination number and the k-tuple domination number, respectively. On the square board, and for even k, the k-domination number is nk/2 when n ≥ (k2 − 2k)/4 and k < 2n. In a similar fashion, the k-tuple domination number is n(k + 1)/2 when k is odd and less than 2n .
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a rook's graph is a graph that represents all legal moves of the rook
Rook (chess)
A rook is a piece in the strategy board game of chess. Formerly the piece was called the castle, tower, marquess, rector, and comes...
chess
Chess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
piece
Chess piece
Chess pieces or chessmen are the pieces deployed on a chessboard to play the game of chess. The pieces vary in abilities, giving them different values in the game...
on a chessboard
Chessboard
A chessboard is the type of checkerboard used in the board game chess, and consists of 64 squares arranged in two alternating colors...
: each vertex represents a square on a chessboard and each edge represents a legal move. Rook's graphs are highly symmetric perfect graph
Perfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
s; they may be characterized in terms of the number of triangles each edge belongs to and by the existence of a 4-cycle connecting each nonadjacent pair of vertices.
Definitions
An n × m rook's graph represents the moves of a rook on an n × m chessboard.Its vertices may be given coordinates (x,y), where 1 ≤ x ≤ n and 1 ≤ y ≤ m. Two vertices (x1,y1) and (x2,y2) are adjacent if and only if either x1 = x2 or y1 = y2; that is, if they belong to the same rank or the same file of the chessboard.
For an n × m rook's graph the total number of vertices is simply nm. For an n × n rook's graph the total number of vertices is simply
and the total number of edges is ; in this case the graph is also known as a two-dimensional Hamming graph or a Latin squareLatin square
In combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column...
graph.
The rook's graph for an n × m chessboard may also be defined as the Cartesian product
Cartesian product of graphs
In graph theory, the Cartesian product G \square H of graphs G and H is a graph such that* the vertex set of G \square H is the Cartesian product V × V; and...
of two complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
s Kn
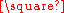Km. The complement graphComplement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of a 2 × n rook's graph is a crown graph
Crown graph
In graph theory, a branch of mathematics, a crown graph on 2n vertices is an undirected graph with two sets of vertices ui and vi and with an edge from ui to vj whenever i ≠ j...
.
Symmetry
Rook's graphs are vertex-transitiveVertex-transitive graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
and (n + m − 2)-regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
; they are the only regular graphs formed from the moves of standard chess pieces in this way (Elkies). When m ≠ n, the symmetries of the rook's graph are formed by independently permuting the rows and columns of the graph. When n = m the graph has additional symmetries that swap the rows and columns; the rook's graph for a square chessboard is symmetric.
Any two vertices in a rook's graph are either at distance one or two from each other, according to whether they are adjacent or nonadjacent respectively. Any two nonadjacent vertices may be transformed into any other two nonadjacent vertices by a symmetry of the graph. When the rook's graph is not square, the pairs of adjacent vertices fall into two orbits of the symmetry group according to whether they are adjacent horizontally or vertically, but when the graph is square any two adjacent vertices may also be mapped into each other by a symmetry and the graph is therefore distance-transitive
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
.
When m and n are relatively prime, the symmetry group Sm×Sn of the rook's graph contains as a subgroup the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Cmn = Cm×Cn that acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
by cyclically permuting the mn vertices; therefore, in this case, the rook's graph is a circulant graph
Circulant graph
In graph theory, a circulant graph is an undirected graph that has a cyclic group of symmetries that includes a symmetry taking any vertex to any other vertex.-Equivalent definitions:Circulant graphs can be described in several equivalent ways:...
.
Perfection
Line graph
In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
of a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
Kn,m — that is, it has one vertex for each edge of Kn,m, and two vertices of the rook's graph are adjacent if and only if the corresponding edges of the complete bipartite graph share a common endpoint. In this view, an edge in the complete bipartite graph from the ith vertex on one side of the bipartition to the jth vertex on the other side corresponds to a chessboard square with coordinates (i,j).
Any bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
is a subgraph of a complete bipartite graph, and correspondingly any line graph of a bipartite graph is an induced subgraph of a rook's graph. The line graphs of bipartite graphs are perfect
Perfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
: in them, and in any of their induced subgraphs, the number of colors needed in any vertex coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
is the same as the number of vertices in the largest complete subgraph
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
. Line graphs of bipartite graphs form an important family of perfect graphs: they are one of a small number of families used by to characterize the perfect graphs and to show that every graph with no odd hole and no odd antihole is perfect. In particular, rook's graphs are themselves perfect.
Because a rook's graph is perfect, the number of colors needed in any coloring of the graph is just the size of its largest clique. The cliques of a rook's graph are the subsets of its rows and columns, and the largest of these have size max(m,n), so this is also the chromatic number of the graph. An n-coloring of an n×n rook's graph may be interpreted as a Latin square
Latin square
In combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column...
: it describes a way of filling the rows and columns of an n×n grid with n different values in such a way that the same value does not appear twice in any row or column.
An independent set
Independent set (graph theory)
In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
in a rook's graph is a set of vertices, no two of which belong to the same row or column of the graph. Perfect graphs may also be described as the graphs in which, in every induced subgraph, the size of the largest independent set is equal to the number of cliques in a partition of the graph's vertices into a minimum number of cliques. In a rook's graph, the sets of rows or the sets of columns (whichever has fewer sets) form such an optimal partition. The size of the largest independent set in the graph is therefore min(m,n). Every color class in every optimal coloring of a rook's graph is a maximum independent set.
Characterization
characterizes the m × n rook's graph as the unique graph having the following properties:- It has mn vertices, each of which is adjacent to n + m − 2 edges.
- mn(m −1)/2 of the edges belong to m − 2 triangles and the remaining mn(n −1)/2 edges belong to n − 2 triangles.
- Any two vertices that are not adjacent to each other belong to a unique 4-cycleCycle (graph theory)In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
.
When n = m, these conditions may be abbreviated by stating that an n×n rook's graph is a strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
with parameters
srg(n2, 2n − 2, n − 2, 2), and that every strongly regular graph with these parameters must be an n×n rook's graph when n≠4. When n=4, there is another strongly regular graph, the Shrikhande graph
Shrikhande graph
In the mathematical field of graph theory, the Shrikhande graph is a named graph discovered by S. S. Shrikhande in 1959. It is a strongly regular graph with 16 vertices and 48 edges, with each vertex having a degree of 6.-Properties:...
, with the same parameters as the 4×4 rook's graph.
The Shrikhande graph can be distinguished from the 4×4 rook's graph in that the neighborhood of any vertex in the Shrikhande graph is connected in a 6-cycle, while in the rook's graph it is connected into two triangles.
Domination
The domination number of a graph is the minimum cardinality among all dominating sets. On the rook's graph a set of vertices is a dominating set if and only if their corresponding squares either occupy, or are a rook's move away from, all squares on the m×n board. For the m×n board the domination number is min(m,n) .On the rook's graph a k-dominating set is a set of vertices whose corresponding squares attack all other squares (via a rook's move) at least k times. A k-tuple dominating set on the rook's graph is a set of vertices whose corresponding squares attack all other squares at least k times and are themselves attacked at least k − 1 times. The minimum cardinality among all k-dominating and k-tuple dominating sets are the k-domination number and the k-tuple domination number, respectively. On the square board, and for even k, the k-domination number is nk/2 when n ≥ (k2 − 2k)/4 and k < 2n. In a similar fashion, the k-tuple domination number is n(k + 1)/2 when k is odd and less than 2n .