A snub polyhedron is a polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 obtained by adding extra triangles around each vertex.

Chiral

Chirality (mathematics)

In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...

snub polyhedra do not have reflection symmetry

Reflection symmetry

Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...

 and hence have two enantiomorphous

Chirality (mathematics)

In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...

 forms which are reflections of each other. Their symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

s are all point groups and are one of:

• O - chiral octahedral symmetry
  Octahedral symmetry
  150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
  
  ;the rotation group of the cube and octahedron
  Octahedron
  In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
  
  ; order 24.
• I - chiral icosahedral symmetry
  Icosahedral symmetry
  A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
  
  ; the rotation group of the icosahedron
  Icosahedron
  In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
  
   and the dodecahedron; order 60.

For example, the snub cube

Snub cube

In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...

:


Snub polyhedra have Wythoff symbol

Wythoff symbol

In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....

 | p q r and by extension, vertex configuration

Vertex configuration

In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...

 3.p.3.q.3.r.

Uniform

There are 12 uniform snub polyhedra, not including the icosahedron

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

 as a snub tetrahedron

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

, the great icosahedron as a retrosnub tetrahedron

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

 and the great disnub dirhombidodecahedron

Great disnub dirhombidodecahedron

In geometry, the great disnub dirhombidodecahedron, also called Skilling's figure, is a uniform star polyhedron.John Skilling discovered this one further uniform polyhedron, by relaxing the condition that only two faces may meet at an edge...

, also known as Skilling's figure.

Snub polyhedron	Image	Original polyhedron	Image	Symmetry group
Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....		Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....		Ih
Great icosahedron		Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....		Ih
Snub cube Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...		Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...		O
Snub dodecahedron Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....		Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...		I
Great snub dodecicosidodecahedron Great snub dodecicosidodecahedron In geometry, the great snub dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U64.- Related polyhedra :It shares its vertices and edges, as well as 20 of its triangular faces and all its pentagrammic faces, with the great dirhombicosidodecahedron,...		Great dodecicosidodecahedron Great dodecicosidodecahedron In geometry, the great dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U61.- Related polyhedra :It shares its vertex arrangement with the truncated great dodecahedron and the uniform compounds of 6 or 12 pentagonal prisms...		I
Snub icosidodecadodecahedron Snub icosidodecadodecahedron In geometry, the snub icosidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U46.- Cartesian coordinates :Cartesian coordinates for the vertices of a snub icosidodecadodecahedron are all the even permutations of...		Icosidodecadodecahedron Icosidodecadodecahedron In geometry, the icosidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U44. Its vertex figure is a crossed quadrilateral.- Related polyhedra :It shares its vertex arrangement with the uniform compounds of 10 or 20 triangular prisms...		I
Snub dodecadodecahedron		Dodecadodecahedron		I
Inverted snub dodecadodecahedron		Dodecadodecahedron		I
Great inverted snub icosidodecahedron		Great icosidodecahedron		I
Great retrosnub icosidodecahedron		Great icosidodecahedron		I
Great snub icosidodecahedron		Great icosidodecahedron		I
Small snub icosicosidodecahedron Small snub icosicosidodecahedron In geometry, the small snub icosicosidodecahedron is a uniform star polyhedron, indexed as U32. It has 112 faces , 180 edges, and 60 vertices.- Convex hull :Its convex hull is a nonuniform truncated icosahedron....		Small icosicosidodecahedron Small icosicosidodecahedron In geometry, the small icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U31.- Related polyhedra :It shares its vertex arrangement with the great stellated truncated dodecahedron...		Ih
Small retrosnub icosicosidodecahedron Small retrosnub icosicosidodecahedron In geometry, the small retrosnub icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U72.- Convex hull :Its convex hull is a nonuniform truncated dodecahedron.- Cartesian coordinates :...		Small icosicosidodecahedron Small icosicosidodecahedron In geometry, the small icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U31.- Related polyhedra :It shares its vertex arrangement with the great stellated truncated dodecahedron...		Ih
Great dirhombicosidodecahedron Great dirhombicosidodecahedron In geometry, the great dirhombicosidodecahedron is a nonconvex uniform polyhedron, indexed last as U75.This is the only uniform polyhedron with more than six faces meeting at a vertex...				Ih
Great disnub dirhombidodecahedron Great disnub dirhombidodecahedron In geometry, the great disnub dirhombidodecahedron, also called Skilling's figure, is a uniform star polyhedron.John Skilling discovered this one further uniform polyhedron, by relaxing the condition that only two faces may meet at an edge...		Great dirhombicosidodecahedron Great dirhombicosidodecahedron In geometry, the great dirhombicosidodecahedron is a nonconvex uniform polyhedron, indexed last as U75.This is the only uniform polyhedron with more than six faces meeting at a vertex...		Ih

Notes:

• The icosahedron
  Icosahedron
  In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
  
  , snub cube
  Snub cube
  In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...
  
   and snub dodecahedron
  Snub dodecahedron
  In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....
  
   are the only three convex
  Convex set
  In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
  
   ones. They are obtained by snubification of the octahedron
  Octahedron
  In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
  
  , cuboctahedron
  Cuboctahedron
  In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
  
   and the icosidodecahedron
  Icosidodecahedron
  In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
  
   - the three convex quasiregular polyhedra
  Quasiregular polyhedron
  In geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...
  
  .
• The only snub polyhedron with the chiral
  Chirality (mathematics)
  In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
  
   octahedral group of symmetries is the snub cube
  Snub cube
  In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...
  
  .
• Only the icosahedron
  Icosahedron
  In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
  
   and the great icosahedron are also regular polyhedra
  Regular polyhedron
  A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
  
  . They are also deltahedra
  Deltahedron
  A deltahedron is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta , which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces...
  
  .
• Only the first two and the last four also have reflective symmetries.

There is also the infinite set of antiprism

Antiprism

In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...

s. They are formed from dihedra

Dihedron

A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...

, degenerate

Degeneracy (mathematics)

In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....

regular polyhedra

Regular polyhedron

A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...

. Those up to hexagonal are listed below.

Snub polyhedron	Image	Original polyhedron	Symmetry group
Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...		Digonal dihedron Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...	Td
Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....		Trigonal dihedron Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...	Oh
Square antiprism Square antiprism In geometry, the square antiprism is the second in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps...		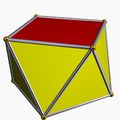Tetragonal dihedron Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...	D4d
Pentagonal antiprism Pentagonal antiprism In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...		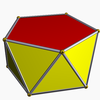Pentagonal dihedron Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...	D5d
Pentagrammic antiprism Pentagrammic antiprism In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U79 as a uniform polyhedron....		Pentagrammic dihedron Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...	D5d
Pentagrammic crossed-antiprism Pentagrammic crossed-antiprism In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams....		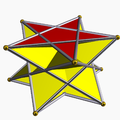Retrogade pentagrammic dihedron Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...	D5d
Hexagonal antiprism Hexagonal antiprism In geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms...		Hexagonal dihedron Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...	D6d

Notes:

• Two of these polyhedra may be constructed from the first two snub polyhedra in the list starting with the icosahedron
  Icosahedron
  In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
  
  : the pentagonal antiprism
  Pentagonal antiprism
  In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...
  
   is a parabidiminished icosahedron
  Johnson solid
  In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
  
   and a pentagrammic crossed-antiprism
  Pentagrammic crossed-antiprism
  In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams....
  
   is a parabidiminished great icosahedron
  Johnson solid
  In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
  
  , also known as a parabireplenished great icosahedron.

Non-uniform

Two Johnson solids are snub polyhedra: the snub disphenoid

Snub disphenoid

In geometry, the snub disphenoid is one of the Johnson solids . It is a three-dimensional solid that has only equilateral triangles as faces, and is therefore a deltahedron. It is not a regular polyhedron because some vertices have four faces and others have five...

 and the snub square antiprism

Snub square antiprism

In geometry, the snub square antiprism is one of theJohnson solids .It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids, although it is a relative of the Icosahedron that has fourfold symmetry instead of...

. Neither is chiral.

Snub polyhedron	Image	Original polyhedron	Image	Symmetry group
Snub disphenoid Snub disphenoid In geometry, the snub disphenoid is one of the Johnson solids . It is a three-dimensional solid that has only equilateral triangles as faces, and is therefore a deltahedron. It is not a regular polyhedron because some vertices have four faces and others have five...		Disphenoid Disphenoid A disphenoid is a polyhedron whose four faces are identical triangles. The faces of a tetragonal disphenoid are isosceles; the faces of a rhombic disphenoid are scalene. If the faces are equilateral triangles, one obtains a regular tetrahedron, which is not normally considered a disphenoid.All the...		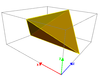D2d
Snub square antiprism Snub square antiprism In geometry, the snub square antiprism is one of theJohnson solids .It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids, although it is a relative of the Icosahedron that has fourfold symmetry instead of...		Square antiprism Square antiprism In geometry, the square antiprism is the second in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps...		D4d

Notes:

• Only the snub disphenoid
  Snub disphenoid
  In geometry, the snub disphenoid is one of the Johnson solids . It is a three-dimensional solid that has only equilateral triangles as faces, and is therefore a deltahedron. It is not a regular polyhedron because some vertices have four faces and others have five...
  
   is a deltahedron
  Deltahedron
  A deltahedron is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta , which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces...
  
  .