
Arithmetic surface
Encyclopedia
In mathematics, an arithmetic surface over a Dedekind domain
R with fraction field
 is a geometric object having one conventional dimension, and one other dimension provided by the infinitude of the primes. When R is the ring of integers
is a geometric object having one conventional dimension, and one other dimension provided by the infinitude of the primes. When R is the ring of integers
Z, this intuition depends on the prime ideal spectrum Spec(Z) being seen as analogous to a line. Arithmetic surfaces arise naturally in diophantine geometry
, when an algebraic curve
defined over K is thought of as having reductions over the fields R/P, where P is a prime ideal of R, for almost all
P; and are helpful in specifying what should happen about the process of reducing to R/P when the most naive way fails to make sense.
Such an object can be less informally defined as an R-scheme
with a non-singular, connected
projective curve
 for a generic fiber
for a generic fiber
and unions of curves (possibly reducible
, singular
, non-reduced
) over the appropriate residue field
for special fibers
.
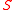 is a scheme
is a scheme
with a morphism
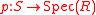 with the following properties:
with the following properties: 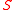 is integral
is integral
, normal
, excellent
, flat
and of finite type over and the generic fiber is a non-singular, connected projective curve over
and the generic fiber is a non-singular, connected projective curve over 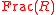 and for other
and for other  in
in 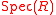 ,
,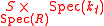
is a union of curves over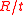 .
.
of a number field (which is the case above). An arithmetic surface is then a regular fibered surface over a Dedekind scheme of dimension one. This generalisation is useful, for example, it allows for base curves which are smooth and projective over finite fields, which is important in positive characteristic.
on arithmetic surfaces since every local ring of dimension one is regular. This is briefly stated as "arithmetic surfaces are regular in codimension one." The theory is developed in Hartshorne's Algebraic Geometry, for example.
over Dedekind domain is a smooth
is a smooth
, proper
arithmetic surface over . The fiber over any maximal ideal
. The fiber over any maximal ideal  is the projective line over the field
is the projective line over the field 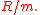
s for elliptic curve
s, initially defined over a global field
, are examples of this construction, and are much studied examples of arithmetic surfaces. There are strong analogies with elliptic fibrations.
offers a solution to the problem presented above. Intuitively, fibers are added at infinity by adding a fiber for each archimedean absolute value of K. A local intersection pairing that extends to the full divisor group can then be defined, with the desired invariance under linear equivalence.
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
R with fraction field
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
 is a geometric object having one conventional dimension, and one other dimension provided by the infinitude of the primes. When R is the ring of integers
is a geometric object having one conventional dimension, and one other dimension provided by the infinitude of the primes. When R is the ring of integersRing of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
Z, this intuition depends on the prime ideal spectrum Spec(Z) being seen as analogous to a line. Arithmetic surfaces arise naturally in diophantine geometry
Diophantine geometry
In mathematics, diophantine geometry is one approach to the theory of Diophantine equations, formulating questions about such equations in terms of algebraic geometry over a ground field K that is not algebraically closed, such as the field of rational numbers or a finite field, or more general...
, when an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
defined over K is thought of as having reductions over the fields R/P, where P is a prime ideal of R, for almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
P; and are helpful in specifying what should happen about the process of reducing to R/P when the most naive way fails to make sense.
Such an object can be less informally defined as an R-scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
with a non-singular, connected
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
projective curve
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
 for a generic fiber
for a generic fiberGeneric point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
and unions of curves (possibly reducible
Irreducible component
In mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :...
, singular
Singular point of an algebraic variety
In mathematics, a singular point of an algebraic variety V is a point P that is 'special' , in the geometric sense that V is not locally flat there. In the case of an algebraic curve, a plane curve that has a double point, such as the cubic curveexhibits at , cannot simply be parametrized near the...
, non-reduced
Glossary of scheme theory
This is a glossary of scheme theory. For an introduction to the theory of schemes in algebraic geometry, see affine scheme, projective space, sheaf and scheme. The concern here is to list the fundamental technical definitions and properties of scheme theory...
) over the appropriate residue field
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
for special fibers
Generic point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
.
Formal definition
In more detail, an arithmetic surface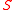 is a scheme
is a schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
with a morphism
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
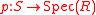 with the following properties:
with the following properties: 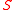 is integral
is integralGlossary of scheme theory
This is a glossary of scheme theory. For an introduction to the theory of schemes in algebraic geometry, see affine scheme, projective space, sheaf and scheme. The concern here is to list the fundamental technical definitions and properties of scheme theory...
, normal
Glossary of scheme theory
This is a glossary of scheme theory. For an introduction to the theory of schemes in algebraic geometry, see affine scheme, projective space, sheaf and scheme. The concern here is to list the fundamental technical definitions and properties of scheme theory...
, excellent
Excellent ring
In mathematics, in the fields of commutative algebra and algebraic geometry, an excellent ring is a Noetherian commutative ring with many of the good properties of complete local rings...
, flat
Flat morphism
In mathematics, in particular in the theory of schemes in algebraic geometry, a flat morphism f from a scheme X to a scheme Y is a morphism such that the induced map on every stalk is a flat map of rings, i.e.,is a flat map for all P in X...
and of finite type over
 and the generic fiber is a non-singular, connected projective curve over
and the generic fiber is a non-singular, connected projective curve over 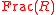 and for other
and for other  in
in 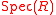 ,
,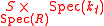
is a union of curves over
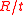 .
.Over a Dedekind Scheme
In even more generality, arithmetic surfaces can be defined over Dedekind schemes, a typical example of which is the spectrum of the ring of integersRing of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
of a number field (which is the case above). An arithmetic surface is then a regular fibered surface over a Dedekind scheme of dimension one. This generalisation is useful, for example, it allows for base curves which are smooth and projective over finite fields, which is important in positive characteristic.
What makes them "arithmetic?"
Arithmetic surfaces are the arithmetic analogue of fibred surfaces with the spectrum of a Dedekind domain replacing the base curve. Such surfaces arise primarily in the context of number theory. In higher dimensions one may also consider arithmetic schemes.Divisors
We can develop a theory of Weil divisorsDivisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
on arithmetic surfaces since every local ring of dimension one is regular. This is briefly stated as "arithmetic surfaces are regular in codimension one." The theory is developed in Hartshorne's Algebraic Geometry, for example.
Projective line
The projective lineProjective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
over Dedekind domain
 is a smooth
is a smoothGlossary of scheme theory
This is a glossary of scheme theory. For an introduction to the theory of schemes in algebraic geometry, see affine scheme, projective space, sheaf and scheme. The concern here is to list the fundamental technical definitions and properties of scheme theory...
, proper
Glossary of scheme theory
This is a glossary of scheme theory. For an introduction to the theory of schemes in algebraic geometry, see affine scheme, projective space, sheaf and scheme. The concern here is to list the fundamental technical definitions and properties of scheme theory...
arithmetic surface over
 . The fiber over any maximal ideal
. The fiber over any maximal ideal  is the projective line over the field
is the projective line over the field 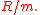
Regular minimal models
Néron modelNéron model
In algebraic geometry, a Néron model for an abelian variety AK defined over a local field K is the "best possible" group scheme AO defined over the ring of integers R of the local field K that becomes isomorphic to AK after base change from R to K.They were introduced by André Néron...
s for elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s, initially defined over a global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
, are examples of this construction, and are much studied examples of arithmetic surfaces. There are strong analogies with elliptic fibrations.
Intersection theory
Given two distinct irreducible divisors and a closed point on the special fiber of an arithmetic surface, we can define the local intersection index of the divisors at the point as you would for any algebraic surface, namely as the dimension of a certain quotient of the local ring at a point. The idea is then to add these local indices up to get a global intersection index. The theory starts to diverge from that of algebraic surfaces when we try to ensure linear equivalent divisors give the same intersection index, this would be used, for example in computing a divisors intersection index with itself. This fails because an arithmetic surface is not complete and a linear equivalence may move an intersection point out to infinity. The simplest resolution to this is to restrict the set of divisors we want to intersect, in particular forcing at least one divisor to be "fibral" (every component is a component of a special fiber) allows us to define a unique intersection pairing having this property, amongst other desirable ones.Arakelov theory
Arakelov theoryArakelov theory
Arakelov theory is an approach to Diophantine geometry, named for Suren Arakelov. It is used to study Diophantine equations in higher dimensions.-Background:...
offers a solution to the problem presented above. Intuitively, fibers are added at infinity by adding a fiber for each archimedean absolute value of K. A local intersection pairing that extends to the full divisor group can then be defined, with the desired invariance under linear equivalence.
See also
- Glossary of arithmetic and Diophantine geometryGlossary of arithmetic and Diophantine geometryThis is a glossary of arithmetic and Diophantine geometry in mathematics, areas growing out of the traditional study of Diophantine equations to encompass large parts of number theory and algebraic geometry...
- Arakelov theoryArakelov theoryArakelov theory is an approach to Diophantine geometry, named for Suren Arakelov. It is used to study Diophantine equations in higher dimensions.-Background:...
- Néron modelNéron modelIn algebraic geometry, a Néron model for an abelian variety AK defined over a local field K is the "best possible" group scheme AO defined over the ring of integers R of the local field K that becomes isomorphic to AK after base change from R to K.They were introduced by André Néron...

