
Cauchy's integral formula
Encyclopedia
In mathematics
, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis
. It expresses the fact that a holomorphic function
defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all derivatives of a holomorphic function. Cauchy's formula shows that, in complex analysis, "differentiation is equivalent to integration": complex differentation, like integration, behaves well under uniform limits – a result denied in real analysis
.
C, f : U → C is a holomorphic function and the closed disk
D = { z : | z − z0| ≤ r} is completely contained in U. Let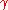 be the circle forming the boundary
be the circle forming the boundary
of D. Then for every a in the interior
of D:
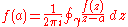
where the contour integral is taken counter-clockwise
.
The proof of this statement uses the Cauchy integral theorem and similarly only requires f to be complex differentiable. Since the reciprocal of the denominator of the integrand in Cauchy's integral formula can be expanded as a power series in the variable (a − z0), it follows that holomorphic functions are analytic
. In particular f is actually infinitely differentiable, with

This formula is sometimes referred to as Cauchy's differentiation formula.
The circle γ can be replaced by any closed rectifiable curve in U which has winding number
one about a. Moreover, as for the Cauchy integral theorem, it is sufficient to require that f be holomorphic in the open region enclosed by the path and continuous on its closure
.
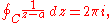
over any circle C centered at a. This can be calculated directly via a parametrization (integration by substitution
)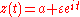 where 0 ≤ t ≤ 2π and ε is the radius of the circle.
where 0 ≤ t ≤ 2π and ε is the radius of the circle.
Letting ε → 0 gives the desired estimate
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
. It expresses the fact that a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all derivatives of a holomorphic function. Cauchy's formula shows that, in complex analysis, "differentiation is equivalent to integration": complex differentation, like integration, behaves well under uniform limits – a result denied in real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
.
Theorem
Suppose U is an open subset of the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
C, f : U → C is a holomorphic function and the closed disk
D = { z : | z − z0| ≤ r} is completely contained in U. Let
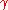 be the circle forming the boundary
be the circle forming the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of D. Then for every a in the interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of D:
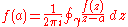
where the contour integral is taken counter-clockwise
Curve orientation
In mathematics, a positively oriented curve is a planar simple closed curve such that when traveling on it one always has the curve interior to the left...
.
The proof of this statement uses the Cauchy integral theorem and similarly only requires f to be complex differentiable. Since the reciprocal of the denominator of the integrand in Cauchy's integral formula can be expanded as a power series in the variable (a − z0), it follows that holomorphic functions are analytic
Holomorphic functions are analytic
In complex analysis, a branch of mathematics, a complex-valued function ƒ of a complex variable z.*is said to be holomorphic at a point a if it is differentiable at every point within some open disk centered at a, and...
. In particular f is actually infinitely differentiable, with

This formula is sometimes referred to as Cauchy's differentiation formula.
The circle γ can be replaced by any closed rectifiable curve in U which has winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
one about a. Moreover, as for the Cauchy integral theorem, it is sufficient to require that f be holomorphic in the open region enclosed by the path and continuous on its closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
.
Proof sketch
By using the Cauchy integral theorem, one can show that the integral over C (or the closed rectifiable curve) is equal to the same integral taken over an arbitrarily small circle around a. Since f(z) is continuous, we can choose a circle small enough on which f(z) is arbitrarily close to f(a). On the other hand, the integral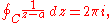
over any circle C centered at a. This can be calculated directly via a parametrization (integration by substitution
Integration by substitution
In calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
)
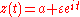 where 0 ≤ t ≤ 2π and ε is the radius of the circle.
where 0 ≤ t ≤ 2π and ε is the radius of the circle.Letting ε → 0 gives the desired estimate
-
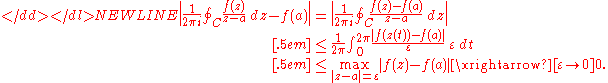
Example
Consider the function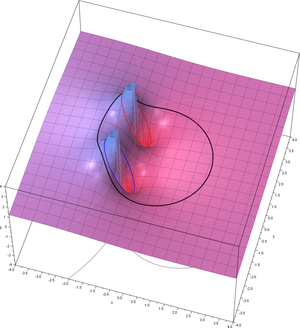
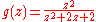
and the contour described by |z| = 2, call it C.
To find the integral of g(z) around the contour, we need to know the singularities of g(z). Observe that we can rewrite g as follows:
where

Clearly the poles become evident, their moduliAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
are less than 2 and thus lie inside the contour and are subject to consideration by the formula. By the Cauchy-Goursat theorem, we can express the integral around the contour as the sum of the integral around z1 and z2 where the contour is a small circle around each pole. Call these contours C1 around z1 and C2 around z2.
Now, around C1, f is analyticHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
(since the contour does not contain the other singularity), and this allows us to write f in the form we require, namely:

and now
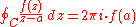

Doing likewise for the other contour:

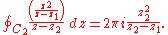
The integral around the original contour C then is the sum of these two integrals:
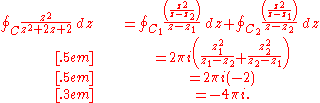
An elementary trick using partial fraction decomposition: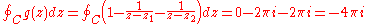
Consequences
The integral formula has broad applications. First, it implies that a function which is holomorphic in an open set is in fact infinitely differentiable there. Furthermore, it is an analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
, meaning that it can be represented as a power series. The proof of this uses the dominated convergence theoremDominated convergence theoremIn measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
and the geometric series applied to
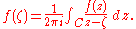
The formula is also used to prove the residue theoremResidue theoremThe residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
, which is a result for meromorphic functionMeromorphic functionIn complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s, and a related result, the argument principleArgument principleIn complex analysis, the argument principle determines the difference between the number of zeros and poles of a meromorphic function by computing a contour integral of the function's logarithmic derivative....
. It is known from Morera's theoremMorera's theoremIn complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic....
that the uniform limit of holomorphic functions is holomorphic. This can also be deduced from Cauchy's integral formula: indeed the formula also holds in the limit and the integrand, and hence the integral, can be expanded as a power series. In addition the Cauchy formulas for the higher order derivatives show that all these derivatives also converge uniformly.
The analog of the Cauchy integral formula in real analysis is the Poisson integral formula for harmonic functionHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s; many of the results for holomorphic functions carry over to this setting. No such results, however, are valid for more general classes of differentiable or real analytic functions. For instance, the existence of the first derivative of a real function need not imply the existence of higher order derivatives, nor in particular the analyticity of the function. Likewise, the uniform limit of a sequence of (real) differentiable functions may fail to be differentiable, or may be differentiable but with a derivative which is not the limit of the derivatives of the members of the sequence.
Smooth functions
A version of Cauchy's integral formula holds for smooth functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s as well, as it is based on Stokes' theoremStokes' theoremIn differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
. Let D be a disc in C and suppose that f is a complex-valued C1 function on the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of D. Then
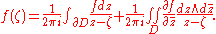
One may use this representation formula to solve the inhomogeneous Cauchy–Riemann equations in D. Indeed, if φ is a function in D, then a particular solution f of the equation is a holomorphic function outside the support of μ. Moreover, if in an open set D,
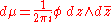
for some φ ∈ Ck(D) (k ≥ 1), then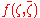 is also in Ck(D) and satisfies the equation
is also in Ck(D) and satisfies the equation
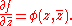
The first conclusion is, succinctly, that the convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
μ∗k(z) of a compactly supported measure with the Cauchy kernel

is a holomorphic function off the support of μ. Here p.v. denotes the principal valueCauchy principal valueIn mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
. The second conclusion asserts that the Cauchy kernel is a fundamental solutionFundamental solutionIn mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
of the Cauchy–Riemann equations. Note that for smooth complex-valued functions f of compact support on C the generalized Cauchy integral formula simplifies to
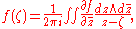
and is a restatement of the fact that, considered as a distributionDistribution (mathematics)In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
, is a fundamental solutionFundamental solutionIn mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
is a fundamental solutionFundamental solutionIn mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
of the Cauchy-Riemann operator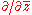 . The generalized Cauchy integral formula can be deduced for any bounded open region X with C1 boundary ∂X from this result and the formula for the distributional derivative of the characteristic functionCharacteristic functionIn mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
. The generalized Cauchy integral formula can be deduced for any bounded open region X with C1 boundary ∂X from this result and the formula for the distributional derivative of the characteristic functionCharacteristic functionIn mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
χX of X:
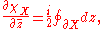
where the distribution on the right hand side denotes contour integration along ∂X.
Several variables
In several complex variablesSeveral complex variablesThe theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, the Cauchy integral formula can be generalized to polydiscs . Let D be the polydisc given as the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of n open discs D1, ..., Dn: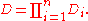
Suppose that f is a holomorphic function in D continuous on the closure of D. Then
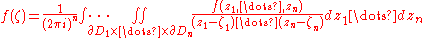
where ζ=(ζ1,...,ζn) ∈ D.
In real algebras
The Cauchy integral formula is generalizable to real vector spaces of two or more dimensions. The insight into this property comes from geometric algebraGeometric algebraGeometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, where objects beyond scalars and vectors (such as planar bivectors and volumetric trivectors) are considered, and a proper generalization of Stokes theorem.
Geometric calculus defines a derivative operator under its geometric product—that is, for a
under its geometric product—that is, for a 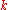 -vector field
-vector field 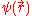 , the derivative
, the derivative 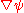 generally contains terms of grade
generally contains terms of grade  and
and  . For example, a vector field (
. For example, a vector field ( ) generally has in its derivative a scalar part, the divergence (
) generally has in its derivative a scalar part, the divergence ( ), and a bivector part, the curl (
), and a bivector part, the curl ( ). This particular derivative operator has a Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
). This particular derivative operator has a Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
:
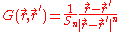
where is the surface area of a unit ball in the space (that is,
is the surface area of a unit ball in the space (that is,  , the circumference of a circle with radius 1, and
, the circumference of a circle with radius 1, and  , the surface area of a sphere with radius 1). By definition of a Green's function,
, the surface area of a sphere with radius 1). By definition of a Green's function, 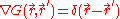 . It is this useful property that can be used, in conjunction with the generalized Stokes theorem:
. It is this useful property that can be used, in conjunction with the generalized Stokes theorem:
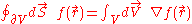
where, for an -dimensional vector space,
-dimensional vector space, 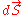 is an
is an 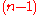 -vector and
-vector and 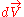 is an
is an  -vector. The function
-vector. The function  can, in principle, be composed of any combination of multivectors. The proof of Cauchy's integral theorem for higher dimensional spaces relies on the using the generalized Stokes theorem on the quantity
can, in principle, be composed of any combination of multivectors. The proof of Cauchy's integral theorem for higher dimensional spaces relies on the using the generalized Stokes theorem on the quantity 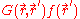 and use of the product rule:
and use of the product rule:

when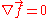 ,
,  is called a monogenic function, the generalization of holomorphic functions to higher-dimensional spaces—indeed, it can be shown that the Cauchy–Riemann condition is just the two-dimensional expression of the monogenic condition. When that condition is met, the second term in the right-hand integral vanishes, leaving only
is called a monogenic function, the generalization of holomorphic functions to higher-dimensional spaces—indeed, it can be shown that the Cauchy–Riemann condition is just the two-dimensional expression of the monogenic condition. When that condition is met, the second term in the right-hand integral vanishes, leaving only

where is that algebra's unit
is that algebra's unit  -vector, the pseudoscalarPseudoscalarIn physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
-vector, the pseudoscalarPseudoscalarIn physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
. The result is
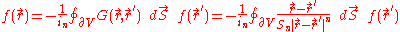
Thus, as in the two-dimensional (complex analysis) case, the value of an analytic (monogenic) function at a point can be found by an integral over the surface surrounding the point, and this is valid not only for scalar functions but vector and general multivector functions as well.
See also
- Cauchy–Riemann equations
- Methods of contour integrationMethods of contour integrationIn the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.Contour integration is closely related to the calculus of residues, a methodology of complex analysis....
- Nachbin's theoremNachbin's theoremIn mathematics, in the area of complex analysis, Nachbin's theorem is commonly used to establish a bound on the growth rates for an analytic function. This article will provide a brief review of growth rates, including the idea of a function of exponential type...
- Morera's theoremMorera's theoremIn complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic....
- Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
generalizes this idea to the non-linear setup - Schwarz integral formula
- Parseval–Gutzmer formula
External links

