Entanglement distillation
Encyclopedia
Entanglement distillation is the transformation of N copies of an arbitrary entangled state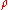 
into some number of approximately pure Bell pairs, using only local operations and classical communication (LOCC
). Entanglement
distillation can in this way overcome the degenerative influence of noisy quantum channel
s by transforming previously shared less entangled pairs into a smaller number of maximally entangled pairs (Bell state
s).
, H. Bernstein, S. Popescu, and B. Schumacher while Entanglement distillation protocols for mixed states were introduced by Bennett, Brassard, Popescu, Schumacher, Smolin and Wootters in a paper later that year in the same journal. Bennett, DiVincenzo, Smolin and Wootters established the connection to quantum error-correction in a ground-breaking paper published in August 1996 also in the journal of Physical Review, which has stimulated a lot of subsequent research.
system can be written as a superposition of possible computational basis qubit states:
, each with an associated complex coefficient 
:
As in the case of a single qubit, the probability of measuring a particular computational basis state
is the amplitude of its associated coefficient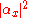 
, subject to the normalization condition 
.
The Bell state is a particularly important example of a two qubit state: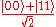
Bell states possess the amazing property that measurement outcomes of a Bell state are correlated. As can be seen from the expression above, the two possible measurement outcomes are zero and one, both with probability of 50%. As a result, a measurement of the second qubit always gives the same result as the measurement of the first qubit.
Bell states can be used to quantify entanglement. Let m be the number of high-fidelity copies of a Bell state that can be produced using LOCC. Given a large number of Bell states the amount of entanglement present in a pure state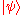
can then be defined as the ratio of 
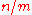, called the distillable entanglement of a particular state 
, which gives a quantified measure of the amount of entanglement present in a given system. The process of entanglement distillation aims to saturate this limiting ratio. The number of copies of a pure state that may be converted into a maximally entangled state is equal to the von Neumann entropy S(p) of the state, which is an extension of the concept of classical entropy for quantum systems. Mathematically, for a given density matrix p, the von Neumann entropy S(p) is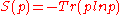 
. Entanglement can then be quantified as the entropy of entanglement, which is the von Neumann entropy of either 
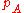or 
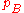as:
Which ranges from 0 for a product state to 1 for a maximally entangled state.
, would like to communicate classical information over a noisy quantum channel. Either classical or quantum information can be transmitted over a quantum channel by encoding the information in a quantum state. With this knowledge, Alice encodes the classical information that she intends to send to Bob in a (quantum) product state, as a tensor product
of reduced density matrices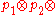
.... where each 
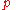is diagonal and can only be used as a one time input for a particular channel 
.
The fidelity of the noisy quantum channel is a measure of how closely the output of a quantum channel resembles the input, and is therefore a measure of how well a quantum channel preserves information. If a pure state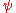
is sent into a quantum channel emerges as the state represented by density matrix 
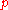, the fidelity of transmission is defined as 
.
The problem that Alice and Bob now face is that quantum communication over large distances depends upon successful distribution of highly entangled quantum states, and due to unavoidable noise in quantum communication channels, the quality of entangled states generally decreases exponentially with channel length as a function of the fidelity of the channel. Entanglement distillation addresses this problem of maintaining a high degree of entanglement between distributed quantum states by transforming N copies of an arbitrary entangled state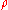
into approximately 
Bell pairs, using only local operations and classical communication. The objective is to share strongly correlated qubits between distant parties (Alice and Bob) in order to allow reliable quantum teleportation
or quantum cryptography
.
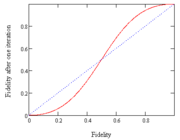Given n particles in the singlet state shared between Alice and Bob, local actions and classical communication will suffice to prepare m arbitrarily good copies of 
with a yield
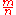approaching 
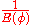as 
.
Let an entangled state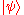
have a Schmidt decomposition
:
where coefficients p(x) form a probability distribution
, and thus are positive valued and sum to unity. The tensor product of this state is then,
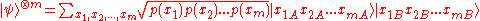
Now, omitting all terms
which are not part of any sequence which is likely to occur with high probability, known as the typical set
:
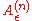the new state is
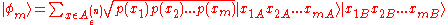
And renormalizing,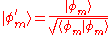
Then the fidelity
as 
.
Suppose that Alice and Bob are in possession of m copies of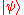
. Alice can perform a measurement onto the typical set 
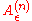subset of 
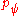, converting the state 
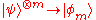with high fidelity. The theorem of typical sequences then shows us that 
is the probability that the given sequence is part of the typical set, and may be made arbitrarily close to 1 for sufficiently large m, and therefore the Schmidt coefficients of the renormalized Bell state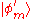 
will be at most a factor 
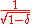larger. Alice and Bob can now obtain a smaller set of n Bell states by performing LOCC on the state 
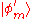with which they can overcome the noise of a quantum channel to communicate successfully.
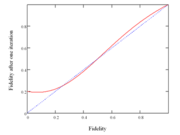Many techniques have been developed for doing entanglement distillation for mixed states, giving a lower bounds on the value of the distillable entanglement 
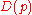for specific classes of states 
.
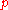One common method involves Alice not using the noisy channel to transmit source states directly but instead preparing a large number of Bell states, sending half of each Bell pair to Bob. The result from transmission through the noisy channel is to create the mixed entangled state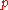
, so that Alice and Bob end up sharing 
copies of 
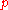. Alice and Bob then perform entanglement distillation, producing 
almost perfectly entangled states from the mixed entangled states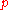 
by performing local unitary operations and measurements on the shared entangled pairs, coordinating their actions through classical messages, and sacrificing some of the entangled pairs to increase the purity of the remaining ones. Alice can now prepare an 
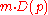qubit state and teleport it to Bob using the 
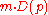Bell pairs which they share with high fidelity. What Alice and Bob have then effectively accomplished is having simulated a noiseless quantum channel using a noisy one, with the aid of local actions and classical communication.
Let
be a general mixed state of two spin-1/2 particles which could have resulted from the transmission of an initially pure singlet state
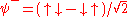
through a noisy channel between Alice and Bob, which will be used to distill some pure entanglement. The fidelity of M
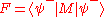
is a convenient expression of its purity relative to a perfect singlet. Suppose that M is already a pure state of two particles
for some 
. The entanglement for 
, as already established, is the von Neumann entropy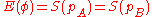 
where
,
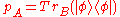and likewise for
, represent the reduced density matrices for either particle. The following protocol is then used:
Repeating the outlined protocol above will distill Werner states whose purity may be chosen to be arbitrarily high
from a collection M of input mixed states of purity 
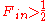but with a yield tending to zero in the limit 
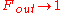. By performing another bilateral XOR operation, this time on a variable number 
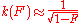of source pairs, as opposed to 1, into each target pair prior to measuring it, the yield can made to approach a positive limit as 
. This method can then be combined with others to obtain an even higher yield.
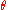) of the n pairs in advance. The method derives its name from Procrustes
because it produces a perfectly entangled state by chopping off the extra probability associated with the larger term in the partial entanglement of the pure states:
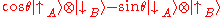
Assuming a collection of particles for which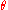
is known as being either less than or greater than 
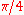the Procrustean method may be carried out by keeping all particles which, when passed through a polarization-dependent absorber, or a polarization-dependent-reflector, which absorb or reflect a fraction 
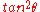of the more likely outcome, are not absorbed or deflected. Therefore, if Alice possesses particles for which 
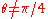, she can separate out particles which are more likely to be measured in the up/down basis, and left with particles in maximally mixed state of spin up and spin down. This treatment corresponds to a POVM
(positive-operator-valued measurement). To obtain a perfectly entangled state of two particles, Alice informs Bob of the result of her generalized measurement while Bob doesn't measure his particle at all but instead discards his if Alice discards hers.
entanglement distillation protocol is to distill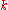
pure ebit
s from
noisy ebit
s where
.
The yield of such a protocol is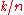
. Two parties can then use the noiseless
ebit
s for quantum communication protocols.
The two parties establish a set of shared noisy ebit
s in the following way.
The sender Alice first prepares
Bell state
s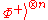
locally. She sends the second qubit
of each
pair over a noisy quantum channel
to a receiver Bob. Let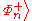
be the state 
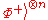rearranged so that all of Alice's qubit
s are on the left and all
of Bob's qubit
s are on the right. The noisy quantum channel
applies a Pauli error in
the error set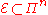
to the set of 
qubit
s sent over
the channel. The sender and receiver then share a set of
noisy ebit
s of
the form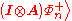
where the identity 
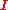acts on Alice's qubit
s and
is some Pauli operator in 
acting on Bob's qubit
s.
A one-way stabilizer entanglement distillation protocol uses a stabilizer code
for the distillation procedure. Suppose the stabilizer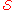
for an
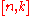quantum error-correcting code has generators 
. The
distillation procedure begins with Alice measuring the
generators in
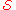. Let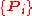 
be the set of the
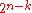projector
s that project onto the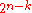
orthogonal subspaces
corresponding to the generators in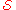
. The measurement projects
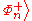randomly onto one of the
subspaces. Each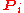 
commute
s with the noisy operator
on Bob's side so that
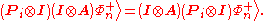
The following important Bell-state matrix identity holds for an arbitrary matrix
:
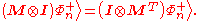
Then the above expression is equal to the following: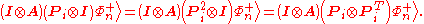
Therefore each of Alice's projectors
projects Bob's qubit
s
onto a subspace
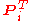corresponding to Alice's projected
subspace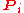
. Alice restores her qubit
s to the simultaneous
+1-eigenspace of the generators in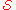
. She sends her measurement
results to Bob. Bob measures the generators in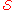
. Bob combines his
measurements with Alice's to determine a syndrome
for the error. He performs a
recovery operation on his qubit
s to reverse the error. He restores his qubit
s
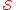. Alice
and Bob both perform the decoding unitary
corresponding to stabilizer
to convert their 
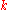logical ebit
s to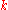
physical ebit
s.
straightforward extension of the above protocol (Luo and Devetak 2007). Their
method converts an entanglement-assisted stabilizer code into an
entanglement-assisted entanglement distillation protocol.
Luo and Devetak form an entanglement distillation protocol that has
entanglement assistance from a few noiseless ebit
s. The crucial assumption for
an entanglement-assisted entanglement distillation protocol is that Alice and
Bob possess
noiseless ebit
s in addition to their
noisy ebit
s. The
total state of the noisy and noiseless ebit
s is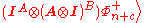
where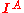
is the 
identity matrix
acting on
Alice's qubit
s and the noisy Pauli operator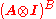
affects Bob's first 
qubit
s only. Thus the last
ebit
s
are noiseless, and Alice and Bob have to correct for errors on the first
ebit
s only.
The protocol proceeds exactly as outlined in the previous section. The only
difference is that Alice and Bob measure the generators in an
entanglement-assisted stabilizer code. Each generator spans over
qubit
s
where the last
qubit
s are noiseless.
We comment on the yield of this entanglement-assisted entanglement
distillation protocol. An entanglement-assisted code has
generators that
each have
Pauli entries. These parameters imply that the entanglement
distillation protocol produces
ebits. But the protocol consumes 
initial noiseless ebit
s as a catalyst for distillation. Therefore the yield of
this protocol is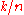
.
connecting Alice and Bob.
In some cases, entanglement distillation may work when conventional quantum error-correction techniques fail. Entanglement distillation protocols are known which can produce a non-zero rate of transmission D(p) for channels which do not allow the transmission of quantum information due to the property that entanglement distillation protocols allow classical communication between parties as opposed to conventional error-correction which prohibits it.
If an entangled pair of particles is shared between two parties, anyone intercepting either particle will alter the overall system, allowing their presence (and the amount of information they have gained) to be determined so long as the particles are in a maximally entangled state. Also, in order to share a secret key string, Alice and Bob must perform the techniques of privacy amplification and information reconciliation to distill a shared secret key string. Information reconciliation is error-correction over a public channel which reconciles errors between the correlated random classical bit strings shared by Alice and Bob while limiting the knowledge that a possible eavesdropper Eve can have about the shared keys. After information reconciliation is used to reconcile possible errors between the shared keys that Alice and Bob possess and limit the possible information Eve could have gained, the technique of privacy amplification is used to distill a smaller subset of bits maximizing Eve's uncertainty about the key.
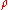into some number of approximately pure Bell pairs, using only local operations and classical communication (LOCCLOCC
LOCC, or Local Operations and Classical Communication, is a method in quantum information theory where a local operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed...
). Entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
distillation can in this way overcome the degenerative influence of noisy quantum channel
Quantum channel
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
s by transforming previously shared less entangled pairs into a smaller number of maximally entangled pairs (Bell state
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s).
History
The limits for entanglement dilution and distillation are due to Bennett, Bernstein, Popescu and Schumacher. Entanglement distillation protocols for pure states were originally presented in a paper by C. H. BennettCharles H. Bennett (computer scientist)
Charles H. Bennett is an IBM Fellow at IBM Research. Bennett's recent work at IBM has concentrated on a re-examination of the physical basis of information, applying quantum physics to the problems surrounding information exchange...
, H. Bernstein, S. Popescu, and B. Schumacher while Entanglement distillation protocols for mixed states were introduced by Bennett, Brassard, Popescu, Schumacher, Smolin and Wootters in a paper later that year in the same journal. Bennett, DiVincenzo, Smolin and Wootters established the connection to quantum error-correction in a ground-breaking paper published in August 1996 also in the journal of Physical Review, which has stimulated a lot of subsequent research.
Quantifying Entanglement
A two qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
system can be written as a superposition of possible computational basis qubit states:
, each with an associated complex coefficient :As in the case of a single qubit, the probability of measuring a particular computational basis state
is the amplitude of its associated coefficient 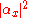, subject to the normalization condition .The Bell state is a particularly important example of a two qubit state:
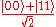
Bell states possess the amazing property that measurement outcomes of a Bell state are correlated. As can be seen from the expression above, the two possible measurement outcomes are zero and one, both with probability of 50%. As a result, a measurement of the second qubit always gives the same result as the measurement of the first qubit.
Bell states can be used to quantify entanglement. Let m be the number of high-fidelity copies of a Bell state that can be produced using LOCC. Given a large number of Bell states the amount of entanglement present in a pure state
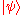can then be defined as the ratio of 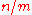, called the distillable entanglement of a particular state , which gives a quantified measure of the amount of entanglement present in a given system. The process of entanglement distillation aims to saturate this limiting ratio. The number of copies of a pure state that may be converted into a maximally entangled state is equal to the von Neumann entropy S(p) of the state, which is an extension of the concept of classical entropy for quantum systems. Mathematically, for a given density matrix p, the von Neumann entropy S(p) is 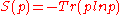. 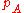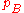Entanglement can then be quantified as the entropy of entanglement, which is the von Neumann entropy of either or as:Which ranges from 0 for a product state to 1 for a maximally entangled state.
Motivation
Suppose that two parties, Alice and BobAlice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
, would like to communicate classical information over a noisy quantum channel. Either classical or quantum information can be transmitted over a quantum channel by encoding the information in a quantum state. With this knowledge, Alice encodes the classical information that she intends to send to Bob in a (quantum) product state, as a tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of reduced density matrices
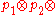.... where each 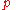is diagonal and can only be used as a one time input for a particular channel .The fidelity of the noisy quantum channel is a measure of how closely the output of a quantum channel resembles the input, and is therefore a measure of how well a quantum channel preserves information. If a pure state
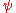is sent into a quantum channel emerges as the state represented by density matrix 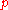, the fidelity of transmission is defined as .The problem that Alice and Bob now face is that quantum communication over large distances depends upon successful distribution of highly entangled quantum states, and due to unavoidable noise in quantum communication channels, the quality of entangled states generally decreases exponentially with channel length as a function of the fidelity of the channel. Entanglement distillation addresses this problem of maintaining a high degree of entanglement between distributed quantum states by transforming N copies of an arbitrary entangled state
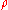into approximately Bell pairs, using only local operations and classical communication. The objective is to share strongly correlated qubits between distant parties (Alice and Bob) in order to allow reliable quantum teleportationQuantum teleportation
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
or quantum cryptography
Quantum cryptography
Quantum key distribution uses quantum mechanics to guarantee secure communication. It enables two parties to produce a shared random secret key known only to them, which can then be used to encrypt and decrypt messages...
.
Pure States
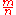with a yield approaching 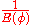as .Let an entangled state
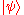have a Schmidt decompositionSchmidt decomposition
In linear algebra, the Schmidt decomposition refers to a particular way of expressing a vector in the tensor product of two inner product spaces. It has applications in quantum information theory and plasticity....
:
where coefficients p(x) form a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, and thus are positive valued and sum to unity. The tensor product of this state is then,
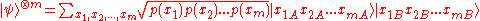
Now, omitting all terms
which are not part of any sequence which is likely to occur with high probability, known as the typical setTypical set
In information theory, the typical set is a set of sequences whose probability is close to two raised to the negative power of the entropy of their source distribution. That this set has total probability close to one is a consequence of the asymptotic equipartition property which is a kind of law...
:
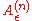the new state is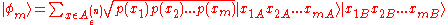And renormalizing,
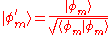
Then the fidelity
Fidelity of quantum states
In quantum information theory, fidelity is a measure of the "closeness" of two quantum states. It is not a metric on the space of density matrices, but it can be used to define the Bures metric on this space.- Motivation :...
as .Suppose that Alice and Bob are in possession of m copies of
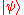. Alice can perform a measurement onto the typical set 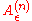subset of 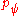, converting the state 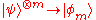with high fidelity. The theorem of typical sequences then shows us that is the probability that the given sequence is part of the typical set, and may be made arbitrarily close to 1 for sufficiently large m, and therefore the Schmidt coefficients of the renormalized Bell state 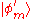will be at most a factor 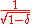larger. Alice and Bob can now obtain a smaller set of n Bell states by performing LOCC on the state 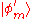with which they can overcome the noise of a quantum channel to communicate successfully.Mixed States
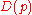for specific classes of states 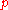.One common method involves Alice not using the noisy channel to transmit source states directly but instead preparing a large number of Bell states, sending half of each Bell pair to Bob. The result from transmission through the noisy channel is to create the mixed entangled state
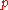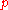, so that Alice and Bob end up sharing copies of . Alice and Bob then perform entanglement distillation, producing almost perfectly entangled states from the mixed entangled states 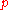by performing local unitary operations and measurements on the shared entangled pairs, coordinating their actions through classical messages, and sacrificing some of the entangled pairs to increase the purity of the remaining ones. Alice can now prepare an 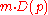qubit state and teleport it to Bob using the 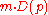Bell pairs which they share with high fidelity. What Alice and Bob have then effectively accomplished is having simulated a noiseless quantum channel using a noisy one, with the aid of local actions and classical communication.Let
be a general mixed state of two spin-1/2 particles which could have resulted from the transmission of an initially pure singlet state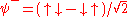through a noisy channel between Alice and Bob, which will be used to distill some pure entanglement. The fidelity of M
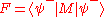
is a convenient expression of its purity relative to a perfect singlet. Suppose that M is already a pure state of two particles
for some . The entanglement for , as already established, is the von Neumann entropy 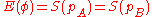where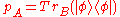,and likewise for
, represent the reduced density matrices for either particle. The following protocol is then used:- Performing a random bilateral rotation on each shared pair, choosing a random SU(2) rotation independently for each pair and applying it locally to both members of the pair transforms the initial general two-spin matrix state M into a rotationally symmetric mixture of the singlet state
and the three triplet states 
and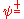 
:
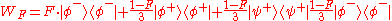
The Werner stateWerner stateA Werner state is a -dimensional bipartite quantum state that is invariant under all unitary operators of the form U \otimes U. That is, it is a quantum state ρ that satisfies\rho = \rho...
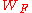has the same purity F as the initial mixed state M from which it was derived due to the singlet's invariance under bilateral rotations. - Each of the two pairs is then acted on by a unilateral rotation, which we can call
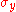, which has the effect of converting them from mainly 
Werner states to mainly 
states with a large component 
of 
while the components of the other three Bell states are equal. - The two impure
states are then acted on by a bilateral XOR, and afterwards the target pair is locally measured along the z axis. The unmeasured source pair is kept if the target pair's spins come out parallel as in the case of both inputs being true 
states; and it is discarded otherwise. - If the source pair has not been discarded it is converted back to a predominantly
state by a unilateral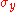 
rotation, and made rotationally symmetric by a random bilateral rotation.
Repeating the outlined protocol above will distill Werner states whose purity may be chosen to be arbitrarily high
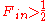from a collection M of input mixed states of purity but with a yield tending to zero in the limit 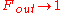. By performing another bilateral XOR operation, this time on a variable number 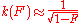of source pairs, as opposed to 1, into each target pair prior to measuring it, the yield can made to approach a positive limit as . This method can then be combined with others to obtain an even higher yield.Procrustean Method
The Procrustean method of entanglement concentration can be used for as little as one partly entangled pair, being more efficient than the Schmidt projection method for entangling less than 5 pairs, and requires Alice and Bob to know the bias (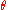) of the n pairs in advance. The method derives its name from ProcrustesProcrustes
In Greek mythology Procrustes or "the stretcher [who hammers out the metal]", also known as Prokoptas or Damastes "subduer", was a rogue smith and bandit from Attica who physically attacked people by stretching them or cutting off their legs, so as to force them to fit the size of an iron bed...
because it produces a perfectly entangled state by chopping off the extra probability associated with the larger term in the partial entanglement of the pure states:
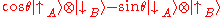
Assuming a collection of particles for which
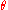is known as being either less than or greater than 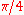the Procrustean method may be carried out by keeping all particles which, when passed through a polarization-dependent absorber, or a polarization-dependent-reflector, which absorb or reflect a fraction 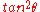of the more likely outcome, are not absorbed or deflected. Therefore, if Alice possesses particles for which 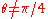, she can separate out particles which are more likely to be measured in the up/down basis, and left with particles in maximally mixed state of spin up and spin down. This treatment corresponds to a POVMPOVM
In functional analysis and quantum measurement theory, a POVM is a measure whose values are non-negative self-adjoint operators on a Hilbert space. It is the most general formulation of a measurement in the theory of quantum physics...
(positive-operator-valued measurement). To obtain a perfectly entangled state of two particles, Alice informs Bob of the result of her generalized measurement while Bob doesn't measure his particle at all but instead discards his if Alice discards hers.
Entanglement Distillation with a Stabilizer Code
The purpose of anentanglement distillation protocol is to distill
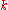pure ebitBell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s from
noisy ebit
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s where
.The yield of such a protocol is
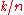. Two parties can then use the noiselessebit
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s for quantum communication protocols.
The two parties establish a set of shared noisy ebit
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s in the following way.
The sender Alice first prepares
Bell stateBell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s
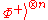locally. She sends the second qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
of each
pair over a noisy quantum channel
Quantum channel
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
to a receiver Bob. Let
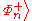be the state 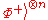rearranged so that all of Alice's qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s are on the left and all
of Bob's qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s are on the right. The noisy quantum channel
Quantum channel
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
applies a Pauli error in
the error set
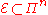to the set of qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s sent over
the channel. The sender and receiver then share a set of
noisy ebitBell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s of
the form
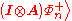where the identity 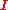acts on Alice's qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s and
is some Pauli operator in acting on Bob's qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s.
A one-way stabilizer entanglement distillation protocol uses a stabilizer code
Stabilizer code
The theory of quantum error correction plays a prominent role in the practical realization and engineering ofquantum computing and quantum communication devices. The first quantumerror-correcting codes are strikingly similar to classical block codes in their...
for the distillation procedure. Suppose the stabilizer
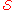for an 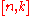quantum error-correcting code has generators . Thedistillation procedure begins with Alice measuring the
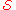generators in. Let 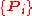be the set of the 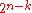projectorProjector
Projector may refer to:*Image projector, a device that projects an image on a surface** Video projector, a device that projects a video signal from computer, home theater system etc.** Movie projector, a device that projects moving pictures from a filmstrip...
s that project onto the
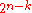orthogonal subspacescorresponding to the generators in
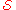. The measurement projects 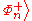randomly onto one of the subspaces. Each 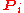commuteCommutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
s with the noisy operator
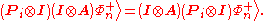
on Bob's side so thatThe following important Bell-state matrix identity holds for an arbitrary matrix
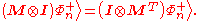
:Then the above expression is equal to the following:
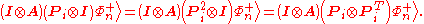
Therefore each of Alice's projectors
projects Bob's qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s
onto a subspace
Subspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
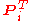corresponding to Alice's projectedsubspace
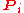. Alice restores her qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s to the simultaneous
+1-eigenspace of the generators in
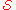. She sends her measurementresults to Bob. Bob measures the generators in
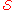. Bob combines hismeasurements with Alice's to determine a syndrome
Syndrome
In medicine and psychology, a syndrome is the association of several clinically recognizable features, signs , symptoms , phenomena or characteristics that often occur together, so that the presence of one or more features alerts the physician to the possible presence of the others...
for the error. He performs a
recovery operation on his qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s to reverse the error. He restores his qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s
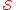. Aliceand Bob both perform the decoding unitary
Unitary
Unitary may refer to:* Unitary construction, in automotive design, another common term for a unibody or monocoque construction**Unitary as chemical weapons opposite of Binary...
corresponding to stabilizer
Stabilizer code
The theory of quantum error correction plays a prominent role in the practical realization and engineering ofquantum computing and quantum communication devices. The first quantumerror-correcting codes are strikingly similar to classical block codes in their...
to convert their 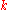logical ebitBell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s to
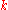physical ebitBell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s.
Entanglement Distillation with an Entanglement-Assisted Stabilizer Code
Luo and Devetak provided astraightforward extension of the above protocol (Luo and Devetak 2007). Their
method converts an entanglement-assisted stabilizer code into an
entanglement-assisted entanglement distillation protocol.
Luo and Devetak form an entanglement distillation protocol that has
entanglement assistance from a few noiseless ebit
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s. The crucial assumption for
an entanglement-assisted entanglement distillation protocol is that Alice and
Bob possess
noiseless ebitBell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s in addition to their
noisy ebitBell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s. The
total state of the noisy and noiseless ebit
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s is
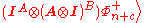
where
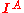is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
acting on
Alice's qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s and the noisy Pauli operator
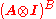affects Bob's first qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s only. Thus the last
ebitBell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s
are noiseless, and Alice and Bob have to correct for errors on the first
ebit
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s only.
The protocol proceeds exactly as outlined in the previous section. The only
difference is that Alice and Bob measure the generators in an
entanglement-assisted stabilizer code. Each generator spans over
qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s
where the last
qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s are noiseless.
We comment on the yield of this entanglement-assisted entanglement
distillation protocol. An entanglement-assisted code has
generators thateach have
Pauli entries. These parameters imply that the entanglementdistillation protocol produces
ebits. But the protocol consumes initial noiseless ebit
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
s as a catalyst for distillation. Therefore the yield of
this protocol is
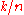.Entanglement Dilution
The reverse process of entanglement distillation is entanglement dilution, where large copies of the Bell state are converted into less entangled states using LOCC with high fidelity. The aim of the entanglement dilution process, then, is to saturate the inverse ratio of n to m, defined as the distillable entanglement.Applications
Besides its important application in quantum communication, entanglement purification also plays a crucial role in error correction for quantum computation, because it can significantly increase the quality of logic operations between different qubits. The role of entanglement distillation is discussed briefly for the following applications.Quantum Error Correction
Entanglement distillation protocols for mixed states can be used as a type of error-correction for quantum communications channels between two parties Alice and Bob, enabling Alice to reliably send mD(p) qubits of information to Bob, where D(p) is the distillable entanglement of p, the state that results when one half of a Bell pair is sent through the noisy channel connecting Alice and Bob.In some cases, entanglement distillation may work when conventional quantum error-correction techniques fail. Entanglement distillation protocols are known which can produce a non-zero rate of transmission D(p) for channels which do not allow the transmission of quantum information due to the property that entanglement distillation protocols allow classical communication between parties as opposed to conventional error-correction which prohibits it.
Quantum Cryptography
The concept of correlated measurement outcomes and entanglement is central to quantum key exchange, and therefore the ability to successfully perform entanglement distillation to obtain maximally entangled states is essential for quantum cryptography.If an entangled pair of particles is shared between two parties, anyone intercepting either particle will alter the overall system, allowing their presence (and the amount of information they have gained) to be determined so long as the particles are in a maximally entangled state. Also, in order to share a secret key string, Alice and Bob must perform the techniques of privacy amplification and information reconciliation to distill a shared secret key string. Information reconciliation is error-correction over a public channel which reconciles errors between the correlated random classical bit strings shared by Alice and Bob while limiting the knowledge that a possible eavesdropper Eve can have about the shared keys. After information reconciliation is used to reconcile possible errors between the shared keys that Alice and Bob possess and limit the possible information Eve could have gained, the technique of privacy amplification is used to distill a smaller subset of bits maximizing Eve's uncertainty about the key.
Quantum Teleportation
In quantum teleportation, a sender wishes to transmit an arbitrary quantum state of a particle to a possibly distant receiver. Quantum teleportation is able to achieve faithful transmission of quantum information by substituting classical communication and prior entanglement for a direct quantum channel. Using teleportation, an arbitrary unknown qubit can be faithfully transmitted via a pair of maximally-entangled qubits shared between sender and receiver, and a 2-bit classical message from the sender to the receiver. Quantum teleportation requires a noiseless quantum channel for sharing perfectly entangled particles, and therefore entanglement distillation satisfies this requirement by providing the noiseless quantum channel and maximally entangled qubits.See also
- Quantum channelQuantum channelIn quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
- Quantum cryptographyQuantum cryptographyQuantum key distribution uses quantum mechanics to guarantee secure communication. It enables two parties to produce a shared random secret key known only to them, which can then be used to encrypt and decrypt messages...
- Quantum entanglementQuantum entanglementQuantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
- Quantum state
- Quantum teleportationQuantum teleportationQuantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
- LOCCLOCCLOCC, or Local Operations and Classical Communication, is a method in quantum information theory where a local operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed...