
Evenness of zero
Encyclopedia

0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
is an even number. In other words, its parity—the quality of an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
being even or odd—is even. Zero fits the definition of "even number": it is an integer multiple
Multiple (mathematics)
In mathematics, a multiple is the product of any quantity and an integer. In other words, for the quantities a and b, we say that b is a multiple of a if b = na for some integer n , which is called the multiplier or coefficient. If a is not zero, this is equivalent to saying that b/a is an integer...
of 2, namely . As a result, zero shares all the properties that characterize even numbers: 0 is evenly divisible by 2, 0 is surrounded on both sides by odd numbers, 0 is the sum
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
of an integer with itself, and a set of 0 objects can be split into two equal sets.
Since definitions can change, another approach is to set them aside and consider how zero fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as , require 0 to be even. Zero is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of even integers, and it is the starting case from which other even natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s are recursively generated
Recursive definition
In mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
. Applications of this recursion from graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
to computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
rely on zero being even. Not only is 0 divisible by 2, it is divisible by every integer. In the binary numeral system
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
used by computers, it is especially relevant that 0 is divisible by every power of 2; in this sense, 0 is the "most even" number of all.
Among the general public, the parity of zero can be a source of confusion. In reaction time experiments, most people are slower to label 0 as even than 2, 4, 6, or 8. In schools, both students and teachers often hold misconceptions that zero is odd, or both even and odd, or neither. Researchers in mathematics education
Mathematics education
In contemporary education, mathematics education is the practice of teaching and learning mathematics, along with the associated scholarly research....
propose that these misconceptions can become learning opportunities. Studying equations like can address students' doubts about calling 0 a number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
and using it in arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
. Discussing the issue in class can spark debates between students, during which they encounter basic principles of mathematical reasoning, such as the importance of definitions. Understanding zero is one goal, but there is also a wider lesson. Evaluating the parity of this exceptional number is an early example of a pervasive theme in mathematics: the abstraction
Abstraction (mathematics)
Abstraction in mathematics is the process of extracting the underlying essence of a mathematical concept, removing any dependence on real world objects with which it might originally have been connected, and generalising it so that it has wider applications or matching among other abstract...
of a familiar concept to an unfamiliar setting.
Why zero is even
It is easy to directly proveMathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
that zero is even:
- A number is called even if it is an integer multiple of 2. Zero is an integer multiple of 2, namely so zero is even.
This proof starts with a standard definition of "even number". It is also possible to explain why zero is even without referring to formal definitions. The following explanations make sense of the idea that zero is even in terms of fundamental number concepts. From this foundation, one can provide a rationale for the definition itself—and its applicability to zero.
Basic explanations
A basic usage for numbers is countingCounting
Counting is the action of finding the number of elements of a finite set of objects. The traditional way of counting consists of continually increasing a counter by a unit for every element of the set, in some order, while marking those elements to avoid visiting the same element more than once,...
. Given a set of objects, one uses a number to describe how many objects are in the set. Zero is the count of no objects; in more formal terms, it is the number of objects in the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
. The concept of parity is used in making groups of two objects. If the objects in a set can be marked off into groups of two, with none left over, then the number of objects is even. If an object is left over, then the number of objects is odd.
The empty set contains zero groups of two, and no object is left over from this grouping, so zero is even. Although it is difficult to depict zero groups of two, or to draw attention to the nonexistence of a leftover object, this conception of the evenness of zero can be illustrated by comparing the empty set with other sets, as in the diagram on the right.
The number line
Number line
In basic mathematics, a number line is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point. Often the integers are shown as specially-marked points evenly spaced on the line...
provides a more uniform way of depicting numbers, including positive numbers, negative numbers, and zero. When even and odd numbers are distinguished visually, their pattern becomes obvious:

Counting
Counting is the action of finding the number of elements of a finite set of objects. The traditional way of counting consists of continually increasing a counter by a unit for every element of the set, in some order, while marking those elements to avoid visiting the same element more than once,...
up or down by twos reaches the other even numbers, and there is no reason to skip over zero.
Parity can be approached in a more formal way using arithmetic expressions. Every integer is either of the form or the former numbers are even and the latter are odd. For example, 1 is odd because and 0 is even because Making a table of these facts then reinforces the number line picture above.
Defining parity
The precise definitionDefinition
A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
of any mathematical term, such as "even" meaning "integer multiple of two", is ultimately a convention
Convention (norm)
A convention is a set of agreed, stipulated or generally accepted standards, norms, social norms or criteria, often taking the form of a custom....
. Unlike "even", some mathematical terms are purposefully constructed to exclude trivial
Trivial (mathematics)
In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
or degenerate cases. Prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s are a famous example. The definition of "prime number" has historically shifted from "positive integer with at most 2 factors" to "positive integer with exactly 2 factors", with the effect that 1 is no longer considered prime. Most authors rationalize this shift by observing that the modern definition more naturally suits mathematical theorems that concern the primes. For example, the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
is easier to state when 1 is not considered prime.
It would be possible to similarly redefine the term "even" in a way that no longer includes zero. However, in this case, the new definition would make it more difficult to state theorems concerning the even numbers. Already the effect can be seen in the algebraic rules governing even and odd numbers. The most relevant rules concern addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
:
- even ± even = even
- odd ± odd = even
- even × integer = even
Inserting appropriate values into the left sides of these rules, one can produce 0 on the right sides:
- 2 − 2 = 0
- −3 + 3 = 0
- 4 × 0 = 0
The above rules would therefore be incorrect if zero were not even. At best they would have to be modified. For example, one test study guide asserts that even numbers are characterized as integer multiples of two, but zero is "neither even nor odd". Accordingly, the guide's rules for even and odd numbers contain exceptions:
- even ± even = even (or zero)
- odd ± odd = even (or zero)
- even × nonzero integer = even
Making an exception for zero in the definition of evenness forces one to make such exceptions in the rules for even numbers. From another perspective, taking the rules obeyed by positive even numbers, and requiring that they continue to hold for integers, forces the usual definition and the evenness of zero.
Mathematical contexts
Countless results in number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
invoke the fundamental theorem of arithmetic and the algebraic properties of even numbers, so the above choices have far-reaching consequences. For example, the fact that numbers have unique factorizations means that one can determine whether a number has an even or odd number of distinct prime factors. Since 1 is not prime, nor does it have prime factors, it is a product of 0
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
distinct primes; since 0 is an even number, 1 has an even number of distinct prime factors. This implies that the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
takes the value , which is necessary for it to be a multiplicative function
Multiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
and for the Möbius inversion formula
Möbius inversion formula
In mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius. Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by...
to work, and affects the exact value of the Mertens function everywhere.
Not being odd
The observation that zero is not odd is sometimes directly applied in a mathematical argument. If an unknown number is proven to be odd, then it cannot be zero. This apparently trivial observation can provide a convenient and revealing proof explaining why a number is nonzero.A classic result of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
states that a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
of odd order always has at least one even vertex
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
. (Already this statement requires zero to be even: the empty graph has an even order, and an isolated vertex is even.) In order to prove the statement, it is actually easier to prove a stronger result: any odd-order graph has an odd number of even vertices. The appearance of this odd number is explained by a still more general result, known as the handshaking lemma
Handshaking lemma
In graph theory, a branch of mathematics, the handshaking lemma is the statement that every finite undirected graph has an even number of vertices with odd degree...
: any graph has an even number of vertices of odd degree. Finally, the even number of odd vertices is naturally explained by the degree sum formula.
Sperner's lemma
Sperner's lemma
In mathematics, Sperner's lemma is a combinatorial analog of the Brouwer fixed point theorem, which follows from it. Sperner's lemma states that every Sperner coloring of a triangulation of an n-dimensional simplex contains a cell colored with a complete set of colors...
is a more advanced application of the same strategy. Rather than prove that there exists a completely labeled subsimplex by a direct construction, it is more convenient to prove that there exist an odd number of such subsimplices through an induction argument. A still stronger statement of the lemma then explains why this number is odd: it naturally breaks down as when one segregates colorings by orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
.
Even-odd alternation

Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
. This idea can be formalized into a recursive definition
Recursive definition
In mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
of the set of even natural numbers:
- 0 is even.
- (n + 1) is even if and only if n is not even.
This definition has the conceptual advantage of relying only on the minimal foundations of the natural numbers: the existence of 0 and of successors. As such, it is useful for computer logic systems such as the Isabelle theorem prover. With this definition, the evenness of zero is not a theorem but an axiom. Indeed, "zero is an even number" may be interpreted as one of the Peano axioms
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
, of which the even natural numbers are a model. A similar construction extends the definition of parity
Even and odd ordinals
In mathematics, even and odd ordinals extend the concept of parity from the natural numbers to the ordinal numbers. They are useful in some transfinite induction proofs.The literature contains a few equivalent definitions of the parity of an ordinal α:...
to transfinite ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s: every limit ordinal is even, including zero, and successor
Successor ordinal
In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
s of even ordinals are odd.
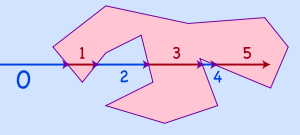
Point in polygon
In computational geometry, the point-in-polygon problem asks whether a given point in the plane lies inside, outside, or on the boundary of a polygon...
test from computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
applies the above ideas. To determine if a point lies within a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
, one casts a ray from infinity to the point and counts the number of times the ray crosses the edge of polygon. The crossing number is even if and only if the point is outside the polygon. This algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
works because if the ray never crosses the polygon, then its crossing number is zero, which is even, and the point is outside. Every time the ray does cross the polygon, the crossing number switches between even and odd, and the point at its tip switches between outside and inside.
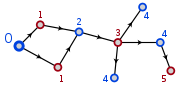
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. A graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
whose vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
are split into two groups, such that two vertices from the same group are never adjacent, is called a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
. If a (connected) graph has no odd cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
s, then an explicit bipartition can be constructed by choosing a base vertex v and coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
every vertex black or white, depending on whether its distance
Distance (graph theory)
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...
from v is even or odd. Since the distance between v and itself is 0, and 0 is even, the base vertex is colored the opposite color as its neighbors, which lie at a distance of 1.
Algebraic patterns
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
. The fact that the additive identity
Additive identity
In mathematics the additive identity of a set which is equipped with the operation of addition is an element which, when added to any element x in the set, yields x...
(zero) is even, together with the evenness of sums and additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
s of even numbers and the associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
of addition, means that the even integers form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. Moreover, the group of even integers under addition is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the group of all integers; this is an elementary example of the subgroup concept. The earlier observation that the rule "even − even = even" forces 0 to be even is part of a general pattern: any nonempty subset of an additive group that is closed under subtraction must be a subgroup, and in particular, must contain the identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
.
Since the even integers form a subgroup of the integers, they partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
the integers into coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s. These cosets may be described as the equivalence classes of the following equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
: if is even. Here, the evenness of zero is directly manifested as the reflexivity
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
of the binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
~. There are only two cosets of this subgroup—the even and odd numbers—and it can be used as a template for subgroups with index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 in other groups as well. A well-known example is the alternating group, a subgroup of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on n letters. The elements of the alternating group, called even permutations, are the products of even numbers of transpositions. The identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
, an empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
of no transpositions, is an even permutation since zero is even; it is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of the group.
Adding in the rule "even × integer = even" means that the even numbers form an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of integers, and the above equivalence relation can be described as equivalence modulo this ideal
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
. In particular, even integers are exactly those integers k where This formulation is useful for investigating integer zeroes of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s.
Degrees of evenness
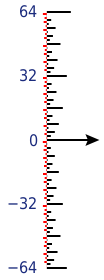
One consequence of this fact appears in computer algorithms such as the Cooley–Tukey FFT, in which numbers appear in bit-reversed order. This ordering has the property that the farther to the left the first 1 occurs in a number's binary expansion, or the more times it is divisible by 2, the sooner it appears. Zero's bit reversal is still zero; it can be divided by 2 any number of times, and its binary expansion does not contain any 1s, so it always comes first. The illustration on the right depicts the evenness of the integers from +64 to −64.

Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
of 2 in the prime factorization of n. But none of these descriptions works for 0; no matter how many times 0 is halved, it can still be halved again. Rather, the usual convention is to set the 2-order of 0 to be infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
as a special case. This convention is not peculiar to the 2-order; it is one of the axioms of an additive valuation in higher algebra.
The powers of two—1, 2, 4, 8, ...—form a simple sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of increasingly even numbers. There are mathematically interesting ways to force such sequences to actually converge
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
to zero, including the construction of the 2-adic number
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s.
History
It is difficult to say when in the history of mathematicsHistory of mathematics
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
the first person examined the parity of zero; there is no well-documented answer.
What is certain is that even and odd numbers were known before the number zero was introduced. Indeed, this historical development parallels children's conceptual development. The algebraic properties of 0, such as the rule were first systematically explored by Indian mathematicians
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
such as Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
in the 7th century—relatively late in comparison to the early history of number theory.
Ancient Greek mathematicians
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
generally considered 2 to be the first even number and 3 the first odd number, and some did not even recognize 2 as even. The number 1 was not truly a number, but a component of all other numbers; as such it had to be both even and odd, and therefore neither truly even nor truly odd. This dual role for 1 was a source of metaphysical discomfort; one historian asserts that the Greeks could have avoided the issue had they known about 0.
Education
The subject of the parity of zero is often treated within the first two or three years of primary educationPrimary education
A primary school is an institution in which children receive the first stage of compulsory education known as primary or elementary education. Primary school is the preferred term in the United Kingdom and many Commonwealth Nations, and in most publications of the United Nations Educational,...
, as the concept of even and odd numbers is introduced and developed.
Students' knowledge

Year One (school)
Year One is an educational year group in schools in many countries including England, Wales, Australia and New Zealand. It is usually the first year of compulsory education and incorporates students aged between five and six.-Australia:...
to Year 6. The data are from Len Frobisher, who conducted a pair of surveys of UK schoolchildren. Frobisher was interested in how knowledge of single-digit parity translates to knowledge of multiple-digit parity, and zero figures prominently in the results.
In a preliminary survey of nearly 400 seven-year-olds, 45% chose even over odd when asked the parity of zero. A follow-up investigation offered more choices: neither, both, and don't know. This time the number of children in the same age range identifying zero as even dropped to 32%. Success in deciding that zero is even initially shoots up and then levels off at around 50% in Years 3 to 6. For comparison, the easiest task, identifying the parity of a single digit, levels off at about 85% success.
In interviews, Frobisher elicited the students' reasoning. One fifth-year decided that 0 was even because it was found on the 2 times table. A couple fourth-years realized that zero can be split into equal parts: "no one gets owt if it's shared out." Another fourth-year reasoned "1 is odd and if I go down it's even." The interviews also revealed the misconceptions behind incorrect responses. A second-year was "quite convinced" that zero was odd, on the basis that "it is the first number you count". A fourth-year referred to 0 as "none" and thought that it was neither odd nor even, since "it's not a number".
More in-depth investigations were conducted by Esther Levenson, Pessia Tsamir, and Dina Tirosh, who interviewed a pair of sixth-grade students who were performing highly in their mathematics class. One student preferred deductive explanations of mathematical claims, while the other preferred practical examples. Both students initially thought that 0 was neither even nor odd, for different reasons. Levenson et al.'s report in the Journal of Mathematical Behavior details the students' reasoning; one of the themes is that their beliefs about the parity of zero are consistent with their concepts of zero and division.
Teachers' knowledge
Researchers of mathematics educationMathematics education
In contemporary education, mathematics education is the practice of teaching and learning mathematics, along with the associated scholarly research....
at the University of Michigan
University of Michigan
The University of Michigan is a public research university located in Ann Arbor, Michigan in the United States. It is the state's oldest university and the flagship campus of the University of Michigan...
used the true-or-false prompt "0 is an even number", among many similar questions, in a 2000–2004 study of 700 primary teachers in the United States
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
. For them the question exemplifies "common knowledge ... that any well-educated adult should have", and it is "ideologically neutral" in that the answer does not vary between traditional
Traditional mathematics
Traditional mathematics is a term used to describe the predominant methods of Mathematics education in the United States in the early-to-mid 20th century. The term is often used to contrast historically predominant methods with non-traditional approaches to math education...
and reform mathematics
Reform mathematics
Reform mathematics is an approach to mathematics education, particularly in North America. It is based on principles explained in 1989 by the National Council of Teachers of Mathematics . The NCTM document, Curriculum and Evaluation Standards for School Mathematics, attempted to set forth a vision...
. Overall performance in the study significantly predicted improvements in students' standardized test
Standardized test
A standardized test is a test that is administered and scored in a consistent, or "standard", manner. Standardized tests are designed in such a way that the questions, conditions for administering, scoring procedures, and interpretations are consistent and are administered and scored in a...
scores after taking the teachers' classes.
It is uncertain how many teachers harbor misconceptions about zero. The Michigan study did not publish data for individual questions. One report comes from Betty Lichtenberg, who wrote an article titled "Zero is an even number" in the journal The Arithmetic Teacher in 1972. Lichtenberg, an associate professor of mathematics education at the University of South Florida
University of South Florida
The University of South Florida, also known as USF, is a member institution of the State University System of Florida, one of the state's three flagship universities for public research, and is located in Tampa, Florida, USA...
, draws on her experience with a course she and her colleagues taught on methods for teaching arithmetic. She reports that several sections of prospective elementary school teachers were given a true-or-false test including the item "Zero is an even number." They found it to be a "tricky question", and about two thirds answered "False".
The literature contains a couple data points concerning teachers' attitudes about students' attitudes. The National Council of Teachers of Mathematics
National Council of Teachers of Mathematics
The National Council of Teachers of Mathematics was founded in 1920. It has grown to be the world's largest organization concerned with mathematics education, having close to 100,000 members across the USA and Canada, and internationally....
's Principles and Standards for School Mathematics
Principles and Standards for School Mathematics
Principles and Standards for School Mathematics are guidelines produced by the National Council of Teachers of Mathematics in 2000, setting forth recommendations for mathematics educators. They form a national vision for preschool through twelfth grade mathematics education in the US and Canada...
records a first grade
First grade
First grade is a year of primary education in schools in the United States and English-speaking provinces of Canada. It is the first school year after kindergarten...
r's argument that zero is an even number: "If zero were odd, then 0 and 1 would be two odd numbers in a row. Even and odd numbers alternate. So 0 must be even..." In a survey of 10 college students preparing to teach mathematics, none of them thought that the argument sufficed as a mathematical proof. When they were told that a first grader had written the argument, most agreed that it was acceptable reasoning for that age level.
Group discussions
Often students will independently ask if zero is even; the Israel National Mathematics Curriculum reminds first gradeFirst grade
First grade is a year of primary education in schools in the United States and English-speaking provinces of Canada. It is the first school year after kindergarten...
teachers that zero is even, but advises that it is unnecessary to mention this unless the class brings it up. In one study, Annie Keith observed a class of 15 second grade
Second grade
In the United States, second grade is a year of primary education. Second grade is the second school year after kindergarten. Students are traditionally 7–8 years old, depending on when their birthday occurs....
students, who convinced each other that zero was an even number based on even-odd alternation and on the possibility of splitting a group of zero things in two equal groups.
Deborah Loewenberg Ball
Deborah Loewenberg Ball
Deborah Loewenberg Ball is an educational researcher noted for her work in mathematics instruction and the mathematical preparation of teachers. She currently is dean of the School of Education at the University of Michigan and William H. Payne Collegiate Professor...
, a researcher specializing in mathematics instruction, has extensively analyzed an episode that occurred in her public school classroom of 22 third grade
Third grade
In the United States, third grade is a year of primary education. It is the third school year after kindergarten. Students are usually 8 – 9 years old, depending on when their birthday occurs....
rs during the 1989–1990 school year. Ball asked the class for comments about even and odd numbers and zero, which they had just been discussing with a group of fourth-graders
Fourth grade
Fourth grade is a year of education in the United States and many other nations. The fourth grade is the fourth school year after kindergarten. Students are usually 9 or 10 years old, depending on their birthday. It is a part of elementary school. In some parts of the United States, fourth grade...
, and over the next six minutes the students made a variety of claims about the parity of zero, the rules for even numbers, and how mathematics is done. The claims about zero alone take many forms: Zero is not even or odd; Zero could be even; Zero is not odd; Zero has to be an even; Zero is not an even number; Zero is always going to be an even number; Zero is not always going to be an even number; Zero is even; Zero is special. Much of the discussion hinges around one student's comment that "even numbers make even numbers", but that zero is "special"; students seem to advance competing definitions of "even", all the while bringing up examples and counterexamples to each other's claims.
Ball later asked her students to reflect on this "particularly long and confusing discussion on even and odd numbers". One student commented that hearing other ideas had helped her understanding, and she now believed for the first time that zero was even. At the same time, another student had originally thought zero to be even but "got sort of mixed up" and was unsure whom to agree with. Ball finds it significant that the latter student expressed a desire to listen further to the discussion: in this sense, both students have learned something valuable about their own learning process. On another occasion, during a discussion on fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
s, Ball asked the class whether voting is a good way to prove what is true in mathematics. One of the students returned to her experience of the discussion on zero, concluding that voting was ineffective in comparison to investigating patterns.
Implications for instruction
Mathematically, no further proof is required, but more explanation is needed in the context of education. One issue concerns the foundations of the proof: the concise definition of "even" given above is not always appropriate. A student in the first years of primary education may not yet have learned what "integer" or "multiple" means, much less how to multiply with 0. Additionally, stating a definition of parity for all integers can seem like an arbitrary conceptual shortcut if the only even numbers investigated so far are 2, 4, 6, 8, and higher. It can help to acknowledge that as the number concept is extended from positive integers to include zero and negative integers, so too number properties such as parity are extended in a nontrivial way.Age-appropriate explanations that zero is even, then, return to the concrete interpretation of parity in terms of paired objects, or they emphasize the even-odd alternation between numbers. Meanwhile misconceptions about 0 must be combated, such as the belief that 0 means nothing and has no properties.
Numerical cognition
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
or a number word is flashed to the subject on a monitor
Computer display
A monitor or display is an electronic visual display for computers. The monitor comprises the display device, circuitry, and an enclosure...
, and a computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
records the time it takes the subject to identify the number as odd or even by striking an appropriate button, such as a Morse key. Stanislas Dehaene
Stanislas Dehaene
Stanislas Dehaene is a professor at the Collège de France, author, and director of INSERM . He has worked on a number of topics, including numerical cognition, the neural basis of reading and the neural correlates of consciousness. Dehaene was one of ten people to be awarded the James S...
, a pioneer in the field of numerical cognition
Numerical cognition
Numerical cognition is a subdiscipline of cognitive science that studies the cognitive, developmental and neural bases of numbers and mathematics. As with many cognitive science endeavors, this is a highly interdisciplinary topic, and includes researchers in cognitive psychology, developmental...
, led a series of such experiments in the early 1990s. They showed that 0 was slower to process than other even numbers. Some variations of the experiment found delays as long as 60 millisecond
Millisecond
A millisecond is a thousandth of a second.10 milliseconds are called a centisecond....
s or about 10% of the average reaction time—a small difference but a significant one.
Dehaene's experiments were not designed specifically to investigate 0, but to compare competing models of how parity information is processed and extracted. The most specific extraction model, the mental calculation hypothesis, suggests that reactions to 0 should be fast: 0 is a small number, and it is easy to calculate . (Subjects are known to compute and name the result of multiplication by zero faster than multiplication of nonzero numbers, although they are slower to verify proposed results like .) The results of the experiments suggested that something quite different was happening: parity information was apparently being recalled from memory along with a cluster of related properties, such as being prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
or a power of two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
. Both the sequence of powers of two and the sequence of positive evens 2, 4, 6, 8, ... are well-distinguished mental categories whose members are prototypically even. Zero belongs to neither list, hence the slower responses.
Repeated experiments have shown a delay at zero for subjects from a variety of national and linguistic backgrounds, representing both left to right
Left to Right
Left to Right is a short story by science fiction writer Isaac Asimov, featured in the short story collection Gold.-Plot synopsis:Robert L. Forward has created a doughnut that is spinning at such a speed that something will interchange...
and right to left writing systems; almost all right-handed; from 17–53 years of age; confronted with number names in numeral
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
form, spelled out, and spelled in a mirror image. Dehaene's group did find one differentiating factor: mathematical expertise. In one of their experiments, students in the École Normale Supérieure
École Normale Supérieure
The École normale supérieure is one of the most prestigious French grandes écoles...
were divided into two groups: those in literary studies and those studying mathematics, physics, or biology. The slowing at 0 was "essentially found in the [literary] group", and in fact, "before the experiment, some L subjects were unsure whether 0 was odd or even and had to be reminded of the mathematical definition".
This strong dependence on familiarity again undermines the mental calculation hypothesis. The effect also suggests that it is inappropriate to include zero in experiments where even and odd numbers are compared as a group. As one study puts it, "Most researchers seem to agree that zero is not a typical even number and should not be investigated as part of the mental number line."
Everyday contexts
Some of the contexts where the parity of zero makes an appearance are purely rhetorical:- It provides material for InternetInternetThe Internet is a global system of interconnected computer networks that use the standard Internet protocol suite to serve billions of users worldwide...
message boards and ask-the-expert websites. - Linguist Joseph Grimes muses that asking "Is zero an even number?" to married couplesMarriageMarriage is a social union or legal contract between people that creates kinship. It is an institution in which interpersonal relationships, usually intimate and sexual, are acknowledged in a variety of ways, depending on the culture or subculture in which it is found...
is a good way to get them to disagree. - Social theorist Anthony WildenAnthony WildenAnthony Wilden is a writer, social theorist, college lecturer, and consultant. Wilden has published numerous books and articles which intersect a number of fields, including systems theory, film theory, structuralism, cybernetics, psychiatry, anthropological theory, water control projects, urban...
proposes that all rules have exceptions, giving an example: "Whole numbers are either odd or even, but zero is neither one nor the other." - Columnist Tony SnowTony SnowRobert Anthony "Tony" Snow was an American journalist, political commentator, television news anchor, syndicated columnist, radio host, musician, and the third White House Press Secretary under President George W. Bush. Snow also worked for President George H. W. Bush as chief speechwriter and...
once wrote, "Question: Name one thing beneath Bill Clinton's dignity. Answer: This is a trick question, like asking whether zero is odd or even. It has no known answer." The attack on ClintonBill ClintonWilliam Jefferson "Bill" Clinton is an American politician who served as the 42nd President of the United States from 1993 to 2001. Inaugurated at age 46, he was the third-youngest president. He took office at the end of the Cold War, and was the first president of the baby boomer generation...
was to be expected; three readers who protested the comparison were more concerned with the mathematical error. - Around the turn of the third millenniumMillenniumA millennium is a period of time equal to one thousand years —from the Latin phrase , thousand, and , year—often but not necessarily related numerically to a particular dating system....
, media outlets noted a pair of unusual milestones: "11/19/1999" was the last calendar dateCalendar dateA date in a calendar is a reference to a particular day represented within a calendar system. The calendar date allows the specific day to be identified. The number of days between two dates may be calculated. For example, "24 " is ten days after "14 " in the Gregorian calendar. The date of a...
composed of all odd digits that would occur for a very long time, and that "02/02/2000" was the first all-even date to occur in a very long time. Since these results make use of 0 being even, some readers disagreed with the idea.
There are also situations where calling zero even, or not, has consequences:
One third-party study guide
Study guide
Study guides can be broad based to facilitate learning in a number of areas, or be resources that foster comprehension of literature, research topics, history, and other subjects....
for the GMAT
Graduate Management Admission Test
The Graduate Management Admission Test is a computer-adaptive standardized test in mathematics and the English language for measuring aptitude to succeed academically in graduate business studies. Business schools use the test as a criterion for admission into graduate business administration...
states that 0 is not even, but the test's authors publish an official study guide that explicitly includes 0 in the even numbers. The correct answers to some of the GMAT's "data sufficiency" questions require that the usual rules for even numbers, such as n being even if is even, hold without exception for 0. The GRE also stipulates that 0 is even. Generally, on standardized test
Standardized test
A standardized test is a test that is administered and scored in a consistent, or "standard", manner. Standardized tests are designed in such a way that the questions, conditions for administering, scoring procedures, and interpretations are consistent and are administered and scored in a...
s, if a question asks about the behavior of even numbers, it might be necessary to keep in mind that zero is even.
The nominal evenness of zero is relevant to odd-even rationing
Odd-even rationing
Odd-even rationing is a method of rationing in which access to some resource is restricted to half the population on any given day. In a common example, cars are allowed to drive or to purchase gasoline on alternate days, according to whether the last digit in their license plate is even or odd...
systems. Car
Čar
Čar is a village in the municipality of Bujanovac, Serbia. According to the 2002 census, the town has a population of 296 people.-References:...
s might be allowed to drive or to purchase gasoline
Gasoline
Gasoline , or petrol , is a toxic, translucent, petroleum-derived liquid that is primarily used as a fuel in internal combustion engines. It consists mostly of organic compounds obtained by the fractional distillation of petroleum, enhanced with a variety of additives. Some gasolines also contain...
on alternate days, according to the parity of the last digit in their license plates. Half of the numbers in a given range end in 0, 2, 4, 6, 8 and the other half in 1, 3, 5, 7, 9, so it makes sense to include 0 with the other even numbers. The relevant legislation sometimes stipulates that zero is even to avoid confusion. In fact, an odd-even restriction on driving in 1977 Paris
Paris
Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...
did lead to confusion when the rules were unclear. On an odd-only day, the police avoided fining drivers whose plates ended in 0, because they did not know whether 0 was even.
In other situations, it can make sense to separate 0 from the other even numbers. On U.S. Navy
United States Navy
The United States Navy is the naval warfare service branch of the United States Armed Forces and one of the seven uniformed services of the United States. The U.S. Navy is the largest in the world; its battle fleet tonnage is greater than that of the next 13 largest navies combined. The U.S...
vessels, even-numbered compartments are found on the port side, but zero is reserved for compartments that intersect the centerline. That is, the numbers read ...6420135... from port to starboard.
In the game of roulette
Roulette
Roulette is a casino game named after a French diminutive for little wheel. In the game, players may choose to place bets on either a single number or a range of numbers, the colors red or black, or whether the number is odd or even....
, the casino
Casino
In modern English, a casino is a facility which houses and accommodates certain types of gambling activities. Casinos are most commonly built near or combined with hotels, restaurants, retail shopping, cruise ships or other tourist attractions...
has an interest in making sure that less than half of the numbers are counted as even. Thus the number 0 does not count as even or odd; a bet placed on either even or odd does not win if the ball falls on "0" or "00". The exact result depends on local rules, but the overall effect is to give the house an edge on "even money
Even money
Even money describes a wagering proposition with even odds - if the bettor loses a bet, he or she stands to lose the same amount of money that the winner of the bet would win . The term has come to have meaning in the wider English usage beyond actual gambling, however, as a way of describing an...
" bets. Similarly, the parity of zero can affect payoffs in prop bet
Proposition bet
In gambling, the term "proposition bet" has two definitions.-Primary definition:...
s when the outcome depends on whether some randomized number is odd or even, and it turns out to be zero. One bookmaker offers a "cricket roulette" in which a batsman
Batting (cricket)
In the sport of cricket, batting is the act or skill of hitting the cricket ball with a cricket bat to score runs or prevent the loss of one's wicket. A player who is currently batting is denoted as a batsman, while the act of hitting the ball is called a shot or stroke...
who is dismissed
Dismissal (cricket)
In the sport of cricket, a dismissal occurs when the batsman is out . Colloquially, the fielding team is also said to have snared, bagged or captured a wicket. At this point a batsman must discontinue batting and leave the field permanently for the innings...
for a duck
Duck (cricket)
In the sport of cricket, a duck refers to a batsman's dismissal for a score of zero.-Origin of the term:The term is a shortening of the term "duck's egg", the latter being used long before Test cricket began...
wins for the bank.
The game of "odds and evens
Odds and evens
Odds and evens, also known as choosies, pick, odds-on poke, or bucking up, is a hand game played between two people, used to decide an issue. This game, a variation of the ancient Morra, is played internationally, especially among children.The individuals prepare by deciding who will be assigned...
" is also affected: if both players cast zero fingers, who wins? Generally zero is counted as even. In fact, playing this game has been suggested as a way of introducing children to the concept that 0 is divisible by 2.

