Glossary of tensor theory
Encyclopedia
This is a glossary of tensor theory. For expositions of tensor theory from different points of view, see:
For some history of the abstract theory see also Multilinear algebra
.
A tensor written in component form is an indexed array. The order of a tensor is the number of indices required. (The rank of tensor used to mean the order, but now it means something different)
Rank
The rank of the tensor is the minimal number of rank-one tensor that you need to sum up to obtain this higher-rank tensor. Rank-one tensors are given the generalization of outer product to m-vectors where m is the order of the tensor.
Dyadic tensor
A dyadic tensor has order two, and may be represented as a square matrix. The conventions aij, aij, and aij, do have different meanings (the position of the index determines its valence (variance), in that the first may represent a quadratic form
, the second a linear transformation
, and the distinction is important in contexts that require tensors that aren't orthogonal (see below). A dyad is a tensor such as aibj, product component-by-component of rank one tensors. In this case it represents a linear transformation, of rank one in the sense of linear algebra
- a clashing terminology that can cause confusion.
Einstein notation
This notation is based on the understanding that in a product of two indexed arrays, if an index letter in the first is repeated in the second, then the (default) interpretation is that the product is summed over all values of the index. For example if aij is a matrix, then under this convention aii is its trace. The Einstein convention is generally used in physics and engineering texts, to the extent that if summation is not to be applied it is normal to note that explicitly.
Kronecker delta
Levi-Civita symbol
Covariant tensor, Contravariant tensor
The classical interpretation is by components. For example in the differential form ai dxj the components ai are a covariant vector. That means all indices are lower; contravariant means all indices are upper.
Mixed tensor
This refers to any tensor with lower and upper indices.
Cartesian tensor
Cartesian tensors are widely used in various branches of continuum mechanics
, such as fluid mechanics
and elasticity
. In classical continuum mechanics
, the space of interest is usually 3-dimensional Euclidean space
, as is the tangent space at each point. If we restrict the local coordinates to be Cartesian coordinates with the same scale centered at the point of interest, the metric tensor
is the Kronecker delta. This means that there is no need to distinguish covariant and contravariant components, and furthermore there is no need to distinguish tensors and tensor densities
. All Cartesian-tensor indices are written as subscripts. Cartesian tensors achieve considerable computational simplification at the cost of generality and of some theoretical insight.
Contraction of a tensor
Raising and lowering indices
Symmetric tensor
Antisymmetric tensor
Multiple cross products
s V and W respectively, then
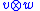
is a tensor in
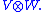
That is, the
operation is a binary operation
, but it takes values in a fresh space (it is in a strong sense external). The
operation is a bilinear map; but no other conditions are applied to it.
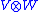is one that is of the form 
.
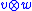It could be written dyadically aibj, or more accurately aibj ei
fj, where the ei are a basis for V and the fj a basis for W. Therefore, unless V and W have the same dimension, the array of components need not be square. Such pure tensors are not generic: if both V and W have dimension > 1, there will be tensors that are not pure, and there will be non-linear conditions for a tensor to satisfy, to be pure. For more see Segre embedding
.
becomes a normal (internal) binary operation
. This is at the cost of T(V) being of infinite dimension, unless V has dimension 0. The free algebra
on a set X is for practical purposes the same as the tensor algebra on the vector space with X as basis.
operation. The quotient space of T(V) on which it becomes an internal operation is the exterior algebra of V; it is a graded algebra
, with the graded piece of weight k being called the k-th exterior power of V.
Tensor field
Tensor density
Lie derivative
Tensor derivative
Differential geometry
This is an operation on fields, that does not always produce a field.
Tensor product of R-algebras
Clifford module
A representation of a Clifford algebra which gives a realisation of a Clifford algebra as a matrix algebra.
Tor functors
These are the derived functor
s of the tensor product, and feature strongly in homological algebra
. The name comes from the torsion subgroup
in abelian group
theory.
Symbolic method of invariant theory
Derived category
Grothendieck's six operations
These are highly abstract approaches used in some parts of geometry.
s, pin group
, pinor
s, spinor field
, Killing spinor
, spin manifold.
- TensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
- Tensor (intrinsic definition)Tensor (intrinsic definition)In mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multi-linear concept...
- Application of tensor theory in engineering science
For some history of the abstract theory see also Multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
.
Classical notation
Tensor orderA tensor written in component form is an indexed array. The order of a tensor is the number of indices required. (The rank of tensor used to mean the order, but now it means something different)
Rank
The rank of the tensor is the minimal number of rank-one tensor that you need to sum up to obtain this higher-rank tensor. Rank-one tensors are given the generalization of outer product to m-vectors where m is the order of the tensor.
Dyadic tensor
Dyadic tensor
In multilinear algebra, a dyadic is a second rank tensor written in a special notation, formed by juxtaposing pairs of vectors, along with a notation for manipulating such expressions analogous to the rules for matrix algebra....
A dyadic tensor has order two, and may be represented as a square matrix. The conventions aij, aij, and aij, do have different meanings (the position of the index determines its valence (variance), in that the first may represent a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
, the second a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
, and the distinction is important in contexts that require tensors that aren't orthogonal (see below). A dyad is a tensor such as aibj, product component-by-component of rank one tensors. In this case it represents a linear transformation, of rank one in the sense of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
- a clashing terminology that can cause confusion.
Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
This notation is based on the understanding that in a product of two indexed arrays, if an index letter in the first is repeated in the second, then the (default) interpretation is that the product is summed over all values of the index. For example if aij is a matrix, then under this convention aii is its trace. The Einstein convention is generally used in physics and engineering texts, to the extent that if summation is not to be applied it is normal to note that explicitly.
Kronecker delta
Levi-Civita symbol
Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
Covariant tensor, Contravariant tensor
The classical interpretation is by components. For example in the differential form ai dxj the components ai are a covariant vector. That means all indices are lower; contravariant means all indices are upper.
Mixed tensor
Mixed tensor
In tensor analysis, a mixed tensor is a tensor which is neither strictly covariant nor strictly contravariant; at least one of the indices of a mixed tensor will be a subscript and at least one of the indices will be a superscript ....
This refers to any tensor with lower and upper indices.
Cartesian tensor
Cartesian tensors are widely used in various branches of continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, such as fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
and elasticity
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
. In classical continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, the space of interest is usually 3-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, as is the tangent space at each point. If we restrict the local coordinates to be Cartesian coordinates with the same scale centered at the point of interest, the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
is the Kronecker delta. This means that there is no need to distinguish covariant and contravariant components, and furthermore there is no need to distinguish tensors and tensor densities
Tensor density
In differential geometry, a tensor density or relative tensor is a generalization of the tensor concept. A tensor density transforms as a tensor when passing from one coordinate system to another , except that it is additionally multiplied or weighted by a power of the Jacobian determinant of the...
. All Cartesian-tensor indices are written as subscripts. Cartesian tensors achieve considerable computational simplification at the cost of generality and of some theoretical insight.
Contraction of a tensor
Tensor contraction
In multilinear algebra, a tensor contraction is an operation on one or more tensors that arises from the natural pairing of a finite-dimensional vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor caused by applying the summation...
Raising and lowering indices
Raising and lowering indices
In mathematics and mathematical physics, given a tensor on a manifold M, in the presence of a nonsingular form on M , one can raise or lower indices: change a type tensor to a tensor or to a tensor...
Symmetric tensor
Antisymmetric tensor
Multiple cross products
Algebraic notation
This avoids the initial use of components, and is distinguished by the explicit use of the tensor product symbol.Tensor product
If v and w are vectors in vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s V and W respectively, then
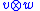
is a tensor in
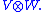
That is, the
operation is a binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
, but it takes values in a fresh space (it is in a strong sense external). The
operation is a bilinear map; but no other conditions are applied to it.Pure tensor
A pure tensor of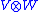 is one that is of the form 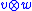.It could be written dyadically aibj, or more accurately aibj ei
fj, where the ei are a basis for V and the fj a basis for W. Therefore, unless V and W have the same dimension, the array of components need not be square. Such pure tensors are not generic: if both V and W have dimension > 1, there will be tensors that are not pure, and there will be non-linear conditions for a tensor to satisfy, to be pure. For more see Segre embeddingSegre embedding
In mathematics, the Segre embedding is used in projective geometry to consider the cartesian product of two or more projective spaces as a projective variety...
.
Tensor algebra
In the tensor algebra T(V) of a vector space V, the operationbecomes a normal (internal) binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
. This is at the cost of T(V) being of infinite dimension, unless V has dimension 0. The free algebra
Free algebra
In mathematics, especially in the area of abstract algebra known as ring theory, a free algebra is the noncommutative analogue of a polynomial ring .-Definition:...
on a set X is for practical purposes the same as the tensor algebra on the vector space with X as basis.
Exterior power
The wedge product is the anti-symmetric form of the operation. The quotient space of T(V) on which it becomes an internal operation is the exterior algebra of V; it is a graded algebraGraded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
, with the graded piece of weight k being called the k-th exterior power of V.
Symmetric power, symmetric algebra
This is the invariant way of constructing polynomial algebras.Tensor field theory
Jacobian matrixTensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
Tensor density
Tensor density
In differential geometry, a tensor density or relative tensor is a generalization of the tensor concept. A tensor density transforms as a tensor when passing from one coordinate system to another , except that it is additionally multiplied or weighted by a power of the Jacobian determinant of the...
Lie derivative
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
Tensor derivative
Differential geometry
Abstract algebra
Tensor product of fieldsTensor product of fields
In abstract algebra, the theory of fields lacks a direct product: the direct product of two fields, considered as a ring is never itself a field. On the other hand it is often required to 'join' two fields K and L, either in cases where K and L are given as subfields of a larger field M, or when K...
This is an operation on fields, that does not always produce a field.
Tensor product of R-algebras
Clifford module
A representation of a Clifford algebra which gives a realisation of a Clifford algebra as a matrix algebra.
Tor functors
These are the derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s of the tensor product, and feature strongly in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
. The name comes from the torsion subgroup
Torsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
in abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
theory.
Symbolic method of invariant theory
Derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
Grothendieck's six operations
These are highly abstract approaches used in some parts of geometry.
Spinors
See: spin group, spin-c group, spinorSpinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s, pin group
Pin group
In mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
, pinor
Piñor
Piñor is a municipality in the Spanish province of Ourense. It has a population of 1552 and an area of 53 km²....
s, spinor field
Spinor field
In particle physics, a spinor field of order 2s describes a particle of spin s, where s is an integer or half-integer. Therefore, a spinor of order 2s contains as much information as a tensor of order s...
, Killing spinor
Killing spinor
Killing spinor is a term used in mathematics and physics. By the more narrow definition, commonly used in mathematics, the term Killing spinor indicates those twistorspinors which are also eigenspinors of the Dirac operator, see Th. Friedrich ,...
, spin manifold.