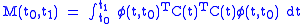Observability
Encyclopedia
Observability, in control theory
, is a measure
for how well internal states of a system
can be inferred by knowledge
of its external output
s. The observability and controllability
of a system are mathematical duals
. The concept of observability was introduced by American-Hungarian scientist Rudolf E. Kalman for linear dynamic systems.
representation). Less formally, this means that from the system's outputs it is possible to determine the behaviour of the entire system. If a system is not observable, this means the current values of some of its states cannot be determined through output sensors: this implies that their value is unknown to the controller
and, consequently, that it will be unable to fulfil the control specifications referred to these outputs.
For time-invariant linear system
s in the state space representation, a convenient test to check if a system is observable exists. Consider a SISO system with
states (see state space
for details about MIMO
systems), if the row rank
of the following observability matrix
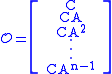
is equal to
, then the system is observable. The rationale for this test is that if 
rows are linearly independent, then each of the 
states is viewable through linear combinations of the output variables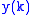 
.
A module designed to estimate the state of a system from measurements of the outputs is called a state observer
or simply an observer for that system.
Observability index
The Observability index
of a linear time-invariant discrete system is the smallest natural number for which is satisfied that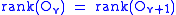 
, where
Detectability
A slightly weaker notion is Detectability. A system is detectable if and only if all of its unobservable modes are stable. Thus even though not all system modes are observable, the ones that are not observable do not require stabilization.
linear
time-variant system
Suppose that the matrices
are given as well as inputs and outputs 
for all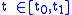 
then it is possible to determine 
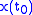to within an additive constant vector which lies in the null space
of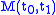
defined by
where
is the state-transition matrix
.
It is possible to determine a unique
if 
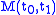is nonsingular. In fact, it is not possible to distinguish the initial state for 
from that of 
if 
is in the null space of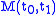 
.
Note that the matrix
defined as above has the following properties:
, 
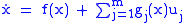. Where 
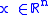the state vector, 
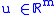the input vector and 
the output vector. 
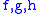are to be smooth vectorfields.
Now define the observation space
to be the space containing all repeated Lie derivative
s. Now the system is observable in
if and only if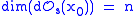 
.
Note: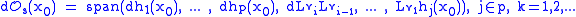
.
Early criteria for observability in nonlinear dynamic systems were discovered by Griffith and Kumar, Kou, Elliot and Tarn, and Singh.
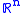
,. Just as observability criteria are used to predict the behavior of Kalman filter
s or other observers in the dynamic system case, observability criteria for sets in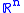
are used to predict the behavior of data reconciliation
and other static estimators. In the nonlinear case, observability can be characterized for individual variables, and also for local estimator behavior rather than just global behavior.
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, is a measure
Measure
- Legal :* Measure of the Church of England is a law passed by the General Synod and the UK Parliament equivalent of an Act* Measure of the National Assembly for Wales, a law specific to Wales passed by the Welsh Assembly between 2007 and 2011...
for how well internal states of a system
System
System is a set of interacting or interdependent components forming an integrated whole....
can be inferred by knowledge
Knowledge
Knowledge is a familiarity with someone or something unknown, which can include information, facts, descriptions, or skills acquired through experience or education. It can refer to the theoretical or practical understanding of a subject...
of its external output
Output
Output is the term denoting either an exit or changes which exit a system and which activate/modify a process. It is an abstract concept, used in the modeling, system design and system exploitation.-In control theory:...
s. The observability and controllability
Controllability
Controllability is an important property of a control system, and the controllability property plays a crucial role in many control problems, such as stabilization of unstable systems by feedback, or optimal control....
of a system are mathematical duals
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
. The concept of observability was introduced by American-Hungarian scientist Rudolf E. Kalman for linear dynamic systems.
Definition
Formally, a system is said to be observable if, for any possible sequence of state and control vectors, the current state can be determined in finite time using only the outputs (this definition is slanted towards the state spaceState space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
representation). Less formally, this means that from the system's outputs it is possible to determine the behaviour of the entire system. If a system is not observable, this means the current values of some of its states cannot be determined through output sensors: this implies that their value is unknown to the controller
Controller (control theory)
In control theory, a controller is a device which monitors and affects the operational conditions of a given dynamical system. The operational conditions are typically referred to as output variables of the system which can be affected by adjusting certain input variables...
and, consequently, that it will be unable to fulfil the control specifications referred to these outputs.
For time-invariant linear system
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
s in the state space representation, a convenient test to check if a system is observable exists. Consider a SISO system with
states (see state spaceState space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
for details about MIMO
MIMO
In radio, multiple-input and multiple-output, or MIMO , is the use of multiple antennas at both the transmitter and receiver to improve communication performance. It is one of several forms of smart antenna technology...
systems), if the row rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of the following observability matrix
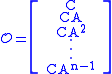
is equal to
, then the system is observable. The rationale for this test is that if rows are linearly independent, then each of the states is viewable through linear combinations of the output variables 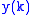.A module designed to estimate the state of a system from measurements of the outputs is called a state observer
State observer
In control theory, a state observer is a system that models a real system in order to provide an estimate of its internal state, given measurements of the input and output of the real system. It is typically a computer-implemented mathematical model....
or simply an observer for that system.
Observability index
The Observability index
of a linear time-invariant discrete system is the smallest natural number for which is satisfied that 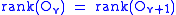, whereDetectability
A slightly weaker notion is Detectability. A system is detectable if and only if all of its unobservable modes are stable. Thus even though not all system modes are observable, the ones that are not observable do not require stabilization.
Continuous Time-Varying System
Consider the continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
time-variant system
Time-variant system
A time-variant system is a system that is not time invariant . Roughly speaking, characteristics of its output depend explicitly upon time.- Overview :...
-
-
.
Suppose that the matrices
are given as well as inputs and outputs for all 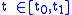then it is possible to determine 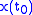to within an additive constant vector which lies in the null spaceNull space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of
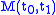defined by
where
is the state-transition matrixState-transition matrix
In control theory, the state-transition matrix is a matrix whose product with the state vector x at an initial time t_0 gives x at a later time t. The state-transition matrix can be used to obtain the general solution of linear dynamical systems...
.
It is possible to determine a unique
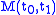if is nonsingular. In fact, it is not possible to distinguish the initial state for from that of if is in the null space of 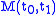.Note that the matrix
defined as above has the following properties:
-
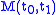is symmetric -
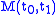is positive semidefinite for 
-
satisfies the linear matrix differential equationMatrix differential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and of its derivatives of various orders...
-
-
-
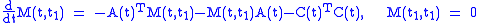
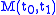satisfies the equation
-
-
-
Nonlinear case
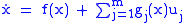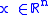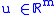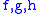Given the system, . Where the state vector, the input vector and the output vector. are to be smooth vectorfields.Now define the observation space
to be the space containing all repeated Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
s. Now the system is observable in
if and only if 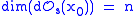.Note:
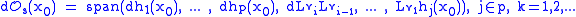.Early criteria for observability in nonlinear dynamic systems were discovered by Griffith and Kumar, Kou, Elliot and Tarn, and Singh.
Static systems and general topological spaces
Observability may also be characterized for steady state systems (systems typically defined in terms of algebraic equations and inequalities), or more generally, for sets in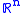,. Just as observability criteria are used to predict the behavior of Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
s or other observers in the dynamic system case, observability criteria for sets in
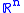are used to predict the behavior of data reconciliationData Validation and Reconciliation
Industrial process data validation and reconciliation or short data validation and reconciliation is a technology which is using process information and mathematical methods in order to automatically correct measurements in industrial processes...
and other static estimators. In the nonlinear case, observability can be characterized for individual variables, and also for local estimator behavior rather than just global behavior.