Wirtinger derivatives
Encyclopedia
In complex analysis of one
and several complex variables
, Wirtinger derivatives (sometimes also called Wirtinger operators), named after Wilhelm Wirtinger
who introduced them in 1927 in the course of his studies on the theory of functions of several complex variables
, are partial differential operators of the first order which behave in a very similar manner to the ordinary derivative
s with respect to one real variable, when applied to holomorphic function
s, antiholomorphic function
s or simply differentiable function
s on complex domains. These operators permit the construction of a differential calculus
for such functions that is entirely analogous to the ordinary differential calculus for functions of real variables
.
at least as early as in the paper , as briefly noted by and by . As a matter of fact, in the third paragraph
of this paper, Henri Poincaré
first defines the complex variable in ℂn and its complex conjugate
as follows
where the index
obviously ranges from 1 to 
. Then he writes the equation defining the functions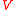 
he calls biharmonique, previously written using partial derivative
s respect to the real
variables
, 
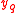for 
,
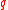ranging from 1 to 
, exactly in the following way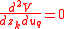
This implies that he implicitly used below: to see this is sufficient to compare equations 2 and 2' of . Apparently, this paper was not noticed by the early savants doing research in the theory of functions of several complex variables
: in the papers of , (and ) and of all fundamental partial differential operators of the theory are expressed directly by using partial derivatives respect to the real and imaginary parts of the complex variables involved. In the long survey paper by (first published in 1913), partial derivatives with respect to each complex variable of a holomorphic function of several complex variables
seem to be meant as formal derivative
s: as a matter of fact when Osgood
express the pluriharmonic operator and the Levi operator, he follows the established practice of Amoroso
, Levi
and Levi-Civita
.
: in the paper , given a complex valued
differentiable function
(in the sense of real analysis
) of one complex variable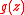
defined in the neighbourhood
of a given point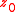
∈ℂ, he defines the areolar derivative as the following limit
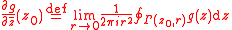
where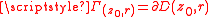
is the boundary
of a disk
of radius
entirely contained in the domain of definition of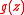 
, i.e. his bounding circle
. This is evidently an alternative definition of Wirtinger derivative respect to the complex conjugate
variable
: it is a more general one, since, as noted a by , the limit may exists for functions that are not even differentiable
at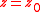
. According to , the first to identify the areolar derivative as a weak derivative
in the sense of Sobolev was Ilia Vekua
. In his following paper, uses this newly defined concept in order to introduce his generalization of Cauchy's integral formula
, the now called Cauchy-Pompeiu formula.
in the paper in order to simplify the calculations of quantities occurring in the theory of functions of several complex variables
: as a result of the introduction of these differential operator
s, the form of all the differential operators commonly used in the theory, like the Levi operator and the Cauchy-Riemann operator
, is considerably simplified and consequently easier to handle. The paper is deliberately written from a formal point of view, i.e. without giving a rigorous derivation of the properties deduced.
by , the monograph
of , and the monograph of which are used here as general references.
ℂ ≡ ℝ2 = {(
, 
) | 
, 
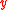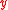∈ ℝ}. The Wirtinger derivatives are defined as the following linear partial differential operators of first order: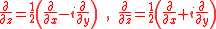
Clearly, the natural domain of definition of these partial differential operators is the space of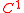
functions on a domain 
⊆ ℝ2, but, since these operators are linear
and have constant coefficients
, they can be readily extended to every space
of generalized function
s.
on the complex field ℂn = ℝ2n = {(
, 
) = (
,..., 
, 
,..., 
) | 
, 
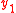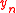∈ ℝ}. The Wirtinger derivatives are defined as the following matrix
linear partial differential operators of first order: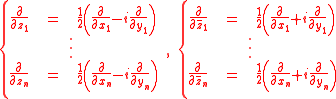
As for Wirtinger derivatives for functions of one complex variable, the natural domain of definition of these partial differential operators is again the space of
functions on a domain 
⊆ ℝ2n, and again, since these operators are linear
and have constant coefficients
, they can be readily extended to every space
of generalized function
s.
∈ ℂn is a complex vector and that 
≡ ( 
, 
) = (
,..., 
, 
,..., 
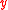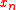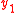) where 
, 
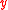are real vectors, with n ≥ 1: also it is assumed that the subset
can be tought as a domain in the real
euclidean space
ℝ2n or in his isomorpic
complex counterpart ℂn. All the proofs are easy consequences of and and of the corresponding properties of the derivatives (ordinary or partial
).
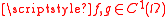and 
are complex number
s, then for all i=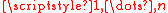
the following equalities hold
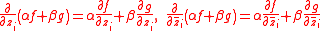
, then for all i=
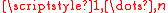the product rule
holds
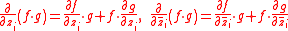
Note that this property implies that Wirtinger derivatives are derivations
from the abstract algebra
point of view, exactly like ordinary derivative
s are.
: for the n > 1 case, to express the chain rule
in its full generality it is necessary to consider two domains
′ ⊆ ℂm and 
″ ⊆ ℂp and two maps
: 
′ → 
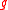and 
: 
→ 
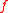″ having natural smoothness
requirements.
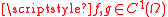, and 
⊆ 
, then the chain rule
holds
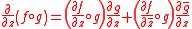
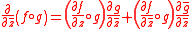
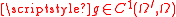and 
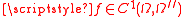, then for all i=
the following form of the chain rule
holds
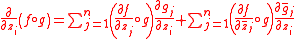
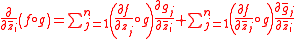
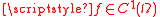, then for all i=
the following equalities hold
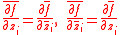
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
and several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, Wirtinger derivatives (sometimes also called Wirtinger operators), named after Wilhelm Wirtinger
Wilhelm Wirtinger
Wilhelm Wirtinger was an Austrian mathematician, working in complex analysis, geometry, algebra, number theory, Lie groups and knot theory.-Biography:...
who introduced them in 1927 in the course of his studies on the theory of functions of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, are partial differential operators of the first order which behave in a very similar manner to the ordinary derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s with respect to one real variable, when applied to holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s, antiholomorphic function
Antiholomorphic function
In mathematics, antiholomorphic functions are a family of functions closely related to but distinct from holomorphic functions....
s or simply differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s on complex domains. These operators permit the construction of a differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
for such functions that is entirely analogous to the ordinary differential calculus for functions of real variables
Function of a real variable
In mathematics, a function of a real variable is a mathematical function whose domain is the real line. More loosely, a function of a real variable is sometimes taken to mean any function whose domain is a subset of the real line....
.
Historical note
Early days (1899–1911): the work of Henri Poincaré
Wirtinger derivatives were used in complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
at least as early as in the paper , as briefly noted by and by . As a matter of fact, in the third paragraph
Paragraph
A paragraph is a self-contained unit of a discourse in writing dealing with a particular point or idea. A paragraph consists of one or more sentences. The start of a paragraph is indicated by beginning on a new line. Sometimes the first line is indented...
of this paper, Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
first defines the complex variable in ℂn and its complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
as follows
where the index
obviously ranges from 1 to . Then he writes the equation defining the functions 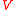he calls biharmonique, previously written using partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s respect to the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
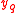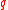, for , ranging from 1 to , exactly in the following way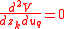This implies that he implicitly used below: to see this is sufficient to compare equations 2 and 2' of . Apparently, this paper was not noticed by the early savants doing research in the theory of functions of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
: in the papers of , (and ) and of all fundamental partial differential operators of the theory are expressed directly by using partial derivatives respect to the real and imaginary parts of the complex variables involved. In the long survey paper by (first published in 1913), partial derivatives with respect to each complex variable of a holomorphic function of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
seem to be meant as formal derivative
Formal derivative
In mathematics, the formal derivative is an operation on elements of a polynomial ring or a ring of formal power series that mimics the form of the derivative from calculus. Though they appear similar, the algebraic advantage of a formal derivative is that it does not rely on the notion of a...
s: as a matter of fact when Osgood
William Fogg Osgood
William Fogg Osgood was an American mathematician, born in Boston.In 1886, he graduated from Harvard, where, after studying at the universities of Göttingen and Erlangen , he was instructor , assistant professor , and thenceforth professor of mathematics...
express the pluriharmonic operator and the Levi operator, he follows the established practice of Amoroso
Luigi Amoroso
- References : . The first paper where a set of necessary and sufficient conditions for the solvability of the Dirichlet problem for holomorphic functions of several variables is given....
, Levi
Eugenio Elia Levi
Eugenio Elia Levi was an Italian mathematician, known for his fundamental contributions in group theory, in the theory of partial differential operators and in the theory of functions of several complex variables: he was the younger brother of Beppo Levi and died in the First World War.-Research...
and Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
.
The work of Dimitrie Pompeiu in 1912 and 1913: a new formulation.
According to , a new step in the definition of the concept was taken by Dimitrie PompeiuDimitrie Pompeiu
-Biography:After studying in Dorohoi and Bucharest, he went to France, where he studied mathematics at the University of Paris . He obtained a Ph.D. degree in mathematics in 1905 with a thesis, On the continuity of complex variable functions, written under the direction of Henri Poincaré...
: in the paper , given a complex valued
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
(in the sense of real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
) of one complex variable
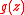defined in the neighbourhoodNeighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of a given point
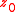∈ℂ, he defines the areolar derivative as the following limitLimit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
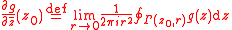
where
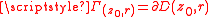is the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of a disk
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
of radius
entirely contained in the domain of definition of 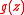, i.e. his bounding circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. This is evidently an alternative definition of Wirtinger derivative respect to the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
: it is a more general one, since, as noted a by , the limit may exists for functions that are not even differentiable
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
at
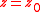. According to , the first to identify the areolar derivative as a weak derivativeWeak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
in the sense of Sobolev was Ilia Vekua
Ilia Vekua
Ilia Vekua Ilia Vekua Ilia Vekua (Georgian: ილია ვეკუა, ; 23 April 1907 in the village of Sheshelety, Kutais Guberniya, Russian Empire (modern day Ochamchira District, Abkhazia, Republic of Georgia – 2 December 1977 in Tbilisi, USSR) was a distinguished Georgian mathematician, specializing in...
. In his following paper, uses this newly defined concept in order to introduce his generalization of Cauchy's integral formula
Cauchy's integral formula
In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...
, the now called Cauchy-Pompeiu formula.
The work of Wilhelm Wirtinger
The first systematic introduction of Wirtinger derivatives seems due to Wilhelm WirtingerWilhelm Wirtinger
Wilhelm Wirtinger was an Austrian mathematician, working in complex analysis, geometry, algebra, number theory, Lie groups and knot theory.-Biography:...
in the paper in order to simplify the calculations of quantities occurring in the theory of functions of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
: as a result of the introduction of these differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s, the form of all the differential operators commonly used in the theory, like the Levi operator and the Cauchy-Riemann operator
Cauchy-Riemann equations
In mathematics, the Cauchy–Riemann differential equations in complex analysis, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which must be satisfied if we know that a complex function is complex differentiable...
, is considerably simplified and consequently easier to handle. The paper is deliberately written from a formal point of view, i.e. without giving a rigorous derivation of the properties deduced.
Formal definition
Despite their ubiquitous use, it seems that there is no text listing all the properties of Wirtinger derivatives: however, fairly complete references are the short course on multidimensional complex analysisSeveral complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
by , the monograph
Monograph
A monograph is a work of writing upon a single subject, usually by a single author.It is often a scholarly essay or learned treatise, and may be released in the manner of a book or journal article. It is by definition a single document that forms a complete text in itself...
of , and the monograph of which are used here as general references.
Functions of one complex variable
Consider the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
ℂ ≡ ℝ2 = {(
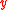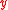, ) | , ∈ ℝ}. The Wirtinger derivatives are defined as the following linear partial differential operators of first order: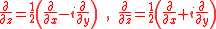Clearly, the natural domain of definition of these partial differential operators is the space of
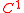functions on a domain ⊆ ℝ2, but, since these operators are linearLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
and have constant coefficients
Constant coefficients
In mathematics, constant coefficients is a term applied to differential operators, and also some difference operators, to signify that they contain no functions of the independent variables, other than constant functions. In other words, it singles out special operators, within the larger class of...
, they can be readily extended to every space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
of generalized function
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
s.
Functions of n > 1 complex variables
Consider the euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
on the complex field ℂn = ℝ2n = {(
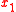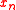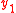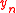, ) = (,..., , ,..., ) | , ∈ ℝ}. The Wirtinger derivatives are defined as the following matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
linear partial differential operators of first order:
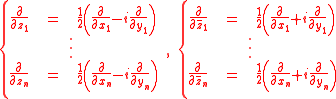
As for Wirtinger derivatives for functions of one complex variable, the natural domain of definition of these partial differential operators is again the space of
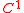functions on a domain ⊆ ℝ2n, and again, since these operators are linearLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
and have constant coefficients
Constant coefficients
In mathematics, constant coefficients is a term applied to differential operators, and also some difference operators, to signify that they contain no functions of the independent variables, other than constant functions. In other words, it singles out special operators, within the larger class of...
, they can be readily extended to every space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
of generalized function
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
s.
Basic properties
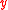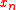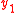In the present section and in the following ones it is assumed that ∈ ℂn is a complex vector and that ≡ ( , ) = (,..., , ,..., ) where , 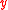are real vectors, with n ≥ 1: also it is assumed that the subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
can be tought as a domain in the realReal field
Real field may refer to:* Real numbers, the numbers that can be represented by infinite decimals* Formally real field, an algebraic field that has the so-called "real" property* Realfield, a spoof of Garfield...
euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
ℝ2n or in his isomorpic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
complex counterpart ℂn. All the proofs are easy consequences of and and of the corresponding properties of the derivatives (ordinary or partial
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
).
Linearity
If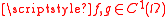 and are complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, then for all i=
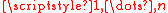the following equalities hold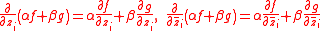Wirtinger derivatives satisfy the product rule
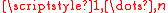If, then for all i= the product ruleProduct rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
holds
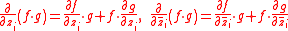
Note that this property implies that Wirtinger derivatives are derivations
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
from the abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
point of view, exactly like ordinary derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s are.
Wirtinger derivatives satisfy the chain rule
This property takes two different forms respectively for functions of one and several complex variablesSeveral complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
: for the n > 1 case, to express the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
in its full generality it is necessary to consider two domains
′ ⊆ ℂm and ″ ⊆ ℂp and two mapsMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
: ′ → and : → ″ having natural smoothnessSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
requirements.
Chain rule for functions of one complex variable
If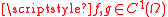, and ⊆ , then the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
holds
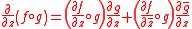
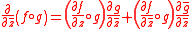
Chain rule for functions of several complex variables
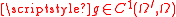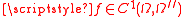If and , then for all i= the following form of the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
holds
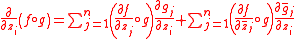
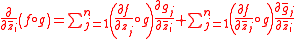
Behavior under conjugation
If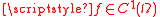, then for all i= 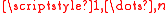the following equalities hold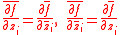See also
- Cauchy–Riemann equations
- Complex analysisComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
- CR-function
- Dolbeault complex
- Dolbeault operator
- Several complex variablesSeveral complex variablesThe theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
- Pluriharmonic functionPluriharmonic functionIn mathematics, precisely in the theory of functions of several complex variables, a pluriharmonic function is a real valued function which is locally the real part of a holomorphic function of several complex variables. Sometimes a such function is referred as n-harmonic function, where n ≥ 2 is...
- Wilhelm WirtingerWilhelm WirtingerWilhelm Wirtinger was an Austrian mathematician, working in complex analysis, geometry, algebra, number theory, Lie groups and knot theory.-Biography:...