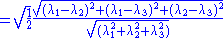Diffusion MRI
Encyclopedia
Diffusion MRI is a magnetic resonance imaging
(MRI) method that produces in vivo
images of biological tissues
weighted with the local microstructural characteristics of water diffusion
, which is capable of showing connections between brain regions. The field of diffusion MRI can be understood in terms of two distinct classes of application—diffusion weighted MRI and diffusion tensor MRI. Diffusion MRI is a key technology in the creation of the human connectome
, which is the structure and organization of the connections throughout the central nervous system
.
In diffusion weighted imaging (DWI), each image voxel
(three dimensional pixel) has an image intensity that reflects a single best measurement of the rate of water diffusion at that location. This measurement is more sensitive to early changes after a stroke than more traditional MRI measurements such as T1 or T2 relaxation rates. DWI is most applicable when the tissue of interest is dominated by isotropic water movement e.g. grey matter
in the cerebral cortex
and major brain nuclei—where the diffusion rate appears to be the same when measured along any axis.
Diffusion tensor imaging (DTI) is important when a tissue—such as the neural axons of white matter
in the brain or muscle fibers in the heart—has an internal fibrous structure analogous to the anisotropy
of some crystals. Water will then diffuse more rapidly in the direction aligned with the internal structure, and more slowly as it moves perpendicular to the preferred direction. This also means that the measured rate of diffusion will differ depending on the direction from which an observer is looking.
Traditionally, in diffusion-weighted imaging (DWI), three gradient-directions are applied, sufficient to estimate the trace of the diffusion tensor or 'average diffusivity', a putative measure of edema
. Clinically, trace-weighted images have proven to be very useful to diagnose vascular stroke
s in the brain, by early detection (within a couple of minutes) of the hypoxic edema.
More extended DTI scans derive neural tract directional information from the data using 3D or multidimensional vector algorithms based on six or more gradient directions, sufficient to compute the diffusion tensor
. The diffusion model is a rather simple model of the diffusion process, assuming homogeneity and linearity of the diffusion within each image voxel. From the diffusion tensor, diffusion anisotropy measures such as the fractional anisotropy (FA), can be computed. Moreover, the principal direction of the diffusion tensor can be used to infer the white-matter connectivity of the brain (i.e. tractography
; trying to see which part of the brain is connected to which other part).
Recently, more advanced models of the diffusion process have been proposed that aim to overcome the weaknesses of the diffusion tensor model. Amongst others, these include q-space imaging and generalized diffusion tensor imaging.
for magnetization would change with the addition of diffusion. Torrey modified Bloch's original description of transverse magnetization to include diffusion terms and the application of a spatially varying gradient. The Bloch-Torrey equation neglecting relaxation is:
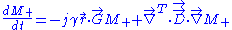
For the simplest case where the diffusion is isotropic the diffusion tensor is
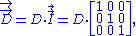
which means that the Bloch–Torrey equation will have the solution
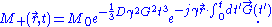
This demonstrates a cubic dependence of transverse magnetization on time. Anisotropic diffusion will have a similar solution method, but with a more complex diffusion tensor.
DWI is a modification of regular MRI techniques, and is an approach which utilizes the measurement of Brownian motion
of molecules. Regular MRI acquisition utilizes the behaviour of protons in water to generate contrast between clinically relevant features of a particular subject. The versatile nature of MRI is due to this capability of producing contrast, called weighting. In a typical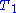
-weighted image, water molecules in a sample are excited with the imposition of a strong magnetic field. This causes many of the protons in water molecules to precess simultaneously, producing signals in MRI. In 
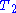-weighted images, contrast is produced by measuring the loss of coherence or synchrony between the water protons. When water is in an environment where it can freely tumble, relaxation tends to take longer. In certain clinical situations, this can generate contrast between an area of pathology and the surrounding healthy tissue.
In diffusion-weighted images, instead of a homogeneous magnetic field, the homogeneity is varied linearly by a pulsed field gradient. Since precession is proportional to the magnet strength, the protons begin to precess at different rates, resulting in dispersion of the phase and signal loss. Another gradient pulse is applied in the same direction but with opposite magnitude to refocus or rephase the spins. The refocusing will not be perfect for protons that have moved during the time interval between the pulses, and the signal measured by the MRI machine is reduced. This reduction in signal due to the application of the pulse gradient can be related to the amount of diffusion that is occurring through the following equation:
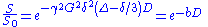
where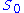
is the signal intensity without the diffusion weighting, 
is the signal with the gradient, 
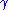is the gyromagnetic ratio, 
is the strength of the gradient pulse,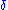 
is the duration of the pulse, 
is the time between the two pulses, and finally, 
is the diffusion-coefficient.
By rearranging the formula to isolate the diffusion-coefficient, it is possible to obtain an idea of the properties of diffusion occurring within a particular voxel
(volume picture element). These values, called apparent diffusion coefficients (ADC) can then be mapped as an image, using diffusion as the contrast.
The first successful clinical application of DWI was in imaging the brain following stroke in adults. Areas which were injured during a stroke showed up "darker" on an ADC map compared to healthy tissue. At about the same time as it became evident to researchers that DWI could be used to assess the severity of injury in adult stroke patients, they also noticed that ADC values varied depending on which way the pulse gradient was applied. This orientation-dependent contrast is generated by diffusion anisotropy, meaning that the diffusion in parts of the brain has directionality. This may be useful for determining structures in the brain which could restrict the flow of water in one direction, such as the myelinated axons of nerve cells (which is affected by multiple sclerosis). However, in imaging the brain following a stroke, it may actually prevent the injury from being seen. To compensate for this, it is necessary to apply a mathematical operator, called a tensor
, to fully characterize the motion of water in all directions.
Diffusion-weighted images are very useful to diagnose vascular strokes in the brain. It is also used more and more in the staging of non small cell lung cancer, where it is a serious candidate to replace positron emission tomography
as the 'gold standard' for this type of disease. Diffusion tensor imaging is being developed for studying the diseases of the white matter
of the brain as well as for studies of other body tissues (see below).
(MRI) technique that enables the measurement of the restricted diffusion of water in tissue in order to produce neural tract images instead of using this data solely for the purpose of assigning contrast or colors to pixels in a cross sectional image. It also provides useful structural information about muscle—including heart muscle, as well as other tissues such as the prostate.
In DTI, each voxel has one or more pairs of parameters: a rate of diffusion and a preferred direction of diffusion—described in terms of three dimensional space—for which that parameter is valid. The properties of each voxel of a single DTI image is usually calculated by vector or tensor math from six or more different diffusion weighted acquisitions, each obtained with a different orientation of the diffusion sensitizing gradients. In some methods, hundreds of measurements—each making up a complete image—are made to generate a single resulting calculated image data set. The higher information content of a DTI voxel makes it extremely sensitive to subtle pathology in the brain. In addition the directional information can be exploited at a higher level of structure to select and follow neural tracts through the brain—a process called tractography
.
A more precise statement of the image acquisition process is that the image-intensities at each position are attenuated, depending on the strength (b-value) and direction of the so-called magnetic diffusion gradient, as well as on the local microstructure in which the water molecules diffuse. The more attenuated the image is at a given position, the greater diffusion there is in the direction of the diffusion gradient. In order to measure the tissue's complete diffusion profile, one needs to repeat the MR scans, applying different directions (and possibly strengths) of the diffusion gradient for each scan.
and magnitude for the principal axis of diffusion in a voxel, accurately modeling the axonal directions that cause the restrictions to the direction of diffusion:
The use of mixed contributions from gradients in the three primary orthogonal axes in order to generate an infinite number of differently oriented gradients for tensor analysis was also identified in 1992 as the basis for accomplishing tensor descriptions of water diffusion in MRI voxels. Both vector and tensor methods provide a "rotationally invariant" measurement—the magnitude will be the same no matter how the tract is oriented relative to the gradient axes—and both provide a three dimensional direction in space, however the tensor method is more efficient and accurate for carrying out tractography. Practically, this class of calculated image places heavy demands on image registration—all of the images collected should ideally be identically shaped and positioned so that the calculated composite image will be correct. In the original FORTRAN program written on a MacIntosh computer by Todd Richards in late 1991, all of the tasks of image registration, and normalized anisotropy assessment (stated as a fraction of 1 and corrected for a "B0" (non-diffusion) basis), as well as calculation of the Euler angles, image generation and tract tracing were simplified by initial development with vectors (three diffusion images plus one non-diffusion image) as opposed to six or more required for a full 2nd rank tensor analysis.
The use of electromagnetic data acquisitions from six or more directions to construct a tensor ellipsoid was known from other fields at the time, as was the use of the tensor ellipsoid to describe diffusion. The inventive step of DTI therefore involved two aspects:
The abstract with the first tractogram appeared at the August 1992 meeting of the Society for Magnetic Resonance in Medicine, Widespread research in the field followed a presentation on March 28, 1993 when Michael Moseley re-presented the tractographic images from the Filler group—describing the new range of neuropathology it had made detectable—and drew attention to this new direction in MRI at a plenary session of Society for Magnetic Resonance Imaging in front of an audience of 700 MRI scientists. Many groups then paid attention to the possibility of using tensor based diffusion anisotropy imaging for neural tract tracing, beginning to optimize tractography. There is now an annual "Fibre Cup" in which various groups compete to provide the most effective new tractographic algorithm. Further advances in the development of tractography can be attributed to Mori, Pierpaoli, Lazar, Conturo and many others.
Diffusion Tensor Imaging became widely used within the MRI community following the work of Basser, Mattliello and LeBihan. Working at the National Institutes of Health, Peter Basser and his coworkers published a series of highly influential papers in the 1990s, establishing diffusion tensor imaging as a viable imaging method
. For this body of work, Basser was awarded the 2008 International Society for Magnetic Resonance in Medicine Gold Medal for "his pioneering and innovative scientific contributions in the development of Diffusion Tensor Imaging (DTI)."
(by Brownian motion
) causes a group of water molecules to move out from a central point, and gradually reach the surface of an ellipsoid if the medium is anisotropic (it would be the surface of a sphere for an isotropic medium). The ellipsoid formalism functions also as a mathematical method of organizing tensor data. Measurement of an ellipsoid tensor further permits a retrospective analysis, to gather information about the process of diffusion in each voxel of the tissue.
In an isotropic medium such as cerebro-spinal fluid, water molecules are moving due to diffusion and they move at equal rates in all directions. By knowing the detailed effects of diffusion gradients we can generate a formula that allows us to convert the signal attenuation
of an MRI voxel into a numerical measure of diffusion—the diffusion coefficient D. When various barriers and restricting factors such as cell membrane
s and microtubule
s interfere with the free diffusion, we are measuring an "apparent diffusion coefficient" or ADC because the measurement misses all the local effects and treats it as if all the movement rates were solely due to Brownian motion. The ADC in anisotropic tissue varies depending on the direction in which it is measured. Diffusion is fast along the length of (parallel to) an axon
, and slower perpendicularly across it.
Once we have measured the voxel from six or more directions and corrected for attenuations due to T2 and T1 effects, we can use information from our calculated ellipsoid tensor to describe what is happening in the voxel. If you consider an ellipsoid sitting at an angle in a Cartesian
grid then you can consider the projection of that ellipse onto the three axes. The three projections can give you the ADC along each of the three axes ADCx, ADCy, ADCz. This leads to the idea of describing the average diffusivity in the voxel which will simply be
/3 = ADCi.
We use the i subscript to signify that this is what the isotropic diffusion coefficient would be with the effects of anisotropy averaged out.
The ellipsoid itself has a principal long axis and then two more small axes that describe its width and depth. All three of these are perpendicular to each other and cross at the center point of the ellipsoid. We call the axes in this setting eigenvectors and the measures of their lengths eigenvalues. The lengths are symbolized by the Greek letter λ
. The long one pointing along the axon direction will be λ1 and the two small axes will have lengths λ2 and λ3. In the setting of the DTI tensor ellipsoid, we can consider each of these as a measure of the diffusivity along each of the three primary axes of the ellipsoid. This is a little different from the ADC since that was a projection on the axis, while λ is an actual measurement of the ellipsoid we have calculated.
The diffusivity along the principal axis, λ1 is also called the longitudinal diffusivity or the axial diffusivity or even the parallel diffusivity λ∥. Historically, this is closest to what Richards originally measured with the vector length in 1991. The diffusivities in the two minor axes are often averaged to produce a measure of radial diffusivity
/2.
This quantity is an assessment of the degree of restriction due to membranes and other effects and proves to be a sensitive measure of degenerative pathology in some neurological conditions. It can also be called the perpendicular diffusivity (λ
).
Another commonly used measure that summarizes the total diffusivity is the Trace—which is the sum of the three eigenvalues,
If we divide this sum by three we have the mean diffusivity
/3.
Aside from describing the amount of diffusion, it is often important to describe the relative degree of anisotropy in a voxel. At one extreme would be the sphere of isotropic diffusion and at the other extreme would be a cigar or pencil shaped very thin prolate spheroid
. The simplest measure is obtained by dividing the longest axis of the ellipsoid by the shortest = (λ1/λ3). However, this proves to be very susceptible to measurement noise, so increasingly complex measures were developed to capture the measure while minimizing the noise. An important element of these calculations is the sum of squares of the diffusivity differences = (λ1 − λ2)2 + (λ1 − λ3)2 + (λ2 − λ3)2. We use the square root of the sum of squares to obtain a sort of weighted average—dominated by the largest component. One objective is to keep the number near 0 if the voxel is spherical but near 1 if it is elongate. This leads to the fractional Anisotropy or FA which is the square root of the sum of squares (SRSS) of the diffusivity differences, divided by the SRSS of the diffusivities. When the second and third axes are small relative to the principal axis, the number in the numerator is almost equal the number in the denominator. We also multiply by the square root of 1/2 = 0.707 to help get the resulting number to be less than one. The whole formula for FA looks like this:
The fractional anisotropy can also be separated into linear, planar, and spherical measures depending on the "shape" of the diffusion ellipsoid. For example, a "cigar" shaped prolate ellipsoid indicates a strongly linear anisotropy, a "flying saucer" or oblate spheroid represents diffusion in a plane, and a sphere is indicative of isotropic diffusion, equal in all directions. If the eigenvalues of the diffusion vector are sorted such that
, then the measures can be calculated as follows:
For the linear case, where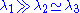
,
Magnetic resonance imaging
Magnetic resonance imaging , nuclear magnetic resonance imaging , or magnetic resonance tomography is a medical imaging technique used in radiology to visualize detailed internal structures...
(MRI) method that produces in vivo
In vivo
In vivo is experimentation using a whole, living organism as opposed to a partial or dead organism, or an in vitro controlled environment. Animal testing and clinical trials are two forms of in vivo research...
images of biological tissues
Tissue (biology)
Tissue is a cellular organizational level intermediate between cells and a complete organism. A tissue is an ensemble of cells, not necessarily identical, but from the same origin, that together carry out a specific function. These are called tissues because of their identical functioning...
weighted with the local microstructural characteristics of water diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
, which is capable of showing connections between brain regions. The field of diffusion MRI can be understood in terms of two distinct classes of application—diffusion weighted MRI and diffusion tensor MRI. Diffusion MRI is a key technology in the creation of the human connectome
Connectome
A connectome is a comprehensive map of neural connections in the brain.The production and study of connectomes, known as connectomics, may range in scale from a detailed map of the full set of neurons and synapses within part or all of the nervous system of an organism to a macro scale description...
, which is the structure and organization of the connections throughout the central nervous system
Central nervous system
The central nervous system is the part of the nervous system that integrates the information that it receives from, and coordinates the activity of, all parts of the bodies of bilaterian animals—that is, all multicellular animals except sponges and radially symmetric animals such as jellyfish...
.
In diffusion weighted imaging (DWI), each image voxel
Voxel
A voxel is a volume element, representing a value on a regular grid in three dimensional space. This is analogous to a pixel, which represents 2D image data in a bitmap...
(three dimensional pixel) has an image intensity that reflects a single best measurement of the rate of water diffusion at that location. This measurement is more sensitive to early changes after a stroke than more traditional MRI measurements such as T1 or T2 relaxation rates. DWI is most applicable when the tissue of interest is dominated by isotropic water movement e.g. grey matter
Grey matter
Grey matter is a major component of the central nervous system, consisting of neuronal cell bodies, neuropil , glial cells and capillaries. Grey matter contains neural cell bodies, in contrast to white matter, which does not and mostly contains myelinated axon tracts...
in the cerebral cortex
Cerebral cortex
The cerebral cortex is a sheet of neural tissue that is outermost to the cerebrum of the mammalian brain. It plays a key role in memory, attention, perceptual awareness, thought, language, and consciousness. It is constituted of up to six horizontal layers, each of which has a different...
and major brain nuclei—where the diffusion rate appears to be the same when measured along any axis.
Diffusion tensor imaging (DTI) is important when a tissue—such as the neural axons of white matter
White matter
White matter is one of the two components of the central nervous system and consists mostly of myelinated axons. White matter tissue of the freshly cut brain appears pinkish white to the naked eye because myelin is composed largely of lipid tissue veined with capillaries. Its white color is due to...
in the brain or muscle fibers in the heart—has an internal fibrous structure analogous to the anisotropy
Anisotropy
Anisotropy is the property of being directionally dependent, as opposed to isotropy, which implies identical properties in all directions. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties An example of anisotropy is the light...
of some crystals. Water will then diffuse more rapidly in the direction aligned with the internal structure, and more slowly as it moves perpendicular to the preferred direction. This also means that the measured rate of diffusion will differ depending on the direction from which an observer is looking.
Traditionally, in diffusion-weighted imaging (DWI), three gradient-directions are applied, sufficient to estimate the trace of the diffusion tensor or 'average diffusivity', a putative measure of edema
Edema
Edema or oedema ; both words from the Greek , oídēma "swelling"), formerly known as dropsy or hydropsy, is an abnormal accumulation of fluid beneath the skin or in one or more cavities of the body that produces swelling...
. Clinically, trace-weighted images have proven to be very useful to diagnose vascular stroke
Stroke
A stroke, previously known medically as a cerebrovascular accident , is the rapidly developing loss of brain function due to disturbance in the blood supply to the brain. This can be due to ischemia caused by blockage , or a hemorrhage...
s in the brain, by early detection (within a couple of minutes) of the hypoxic edema.
More extended DTI scans derive neural tract directional information from the data using 3D or multidimensional vector algorithms based on six or more gradient directions, sufficient to compute the diffusion tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
. The diffusion model is a rather simple model of the diffusion process, assuming homogeneity and linearity of the diffusion within each image voxel. From the diffusion tensor, diffusion anisotropy measures such as the fractional anisotropy (FA), can be computed. Moreover, the principal direction of the diffusion tensor can be used to infer the white-matter connectivity of the brain (i.e. tractography
Tractography
In neuroscience, tractography is a procedure to demonstrate the neural tracts.It uses special techniques of magnetic resonance imaging , and computer-based image analysis.The results are presented in two- and three-dimensional images....
; trying to see which part of the brain is connected to which other part).
Recently, more advanced models of the diffusion process have been proposed that aim to overcome the weaknesses of the diffusion tensor model. Amongst others, these include q-space imaging and generalized diffusion tensor imaging.
Bloch–Torrey equation
In 1956, H.C. Torrey mathematically showed how the Bloch equationsBloch equations
In physics and chemistry, specifically in NMR or MRI , or ESR the Bloch equations are a set of macroscopic equations that are used to calculate the nuclear magnetization M = as a function of time when relaxation times T1 and T2 are present...
for magnetization would change with the addition of diffusion. Torrey modified Bloch's original description of transverse magnetization to include diffusion terms and the application of a spatially varying gradient. The Bloch-Torrey equation neglecting relaxation is:
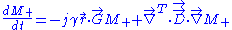
For the simplest case where the diffusion is isotropic the diffusion tensor is
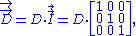
which means that the Bloch–Torrey equation will have the solution
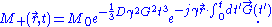
This demonstrates a cubic dependence of transverse magnetization on time. Anisotropic diffusion will have a similar solution method, but with a more complex diffusion tensor.
Diffusion-weighted imaging
Diffusion-weighted imaging is an MRI method that produces in vivo magnetic resonance images of biological tissues weighted with the local characteristics of water diffusion.DWI is a modification of regular MRI techniques, and is an approach which utilizes the measurement of Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
of molecules. Regular MRI acquisition utilizes the behaviour of protons in water to generate contrast between clinically relevant features of a particular subject. The versatile nature of MRI is due to this capability of producing contrast, called weighting. In a typical
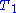-weighted image, water molecules in a sample are excited with the imposition of a strong magnetic field. This causes many of the protons in water molecules to precess simultaneously, producing signals in MRI. In 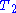-weighted images, contrast is produced by measuring the loss of coherence or synchrony between the water protons. When water is in an environment where it can freely tumble, relaxation tends to take longer. In certain clinical situations, this can generate contrast between an area of pathology and the surrounding healthy tissue.In diffusion-weighted images, instead of a homogeneous magnetic field, the homogeneity is varied linearly by a pulsed field gradient. Since precession is proportional to the magnet strength, the protons begin to precess at different rates, resulting in dispersion of the phase and signal loss. Another gradient pulse is applied in the same direction but with opposite magnitude to refocus or rephase the spins. The refocusing will not be perfect for protons that have moved during the time interval between the pulses, and the signal measured by the MRI machine is reduced. This reduction in signal due to the application of the pulse gradient can be related to the amount of diffusion that is occurring through the following equation:
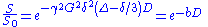
where
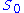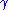is the signal intensity without the diffusion weighting, is the signal with the gradient, is the gyromagnetic ratio, is the strength of the gradient pulse, 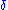is the duration of the pulse, is the time between the two pulses, and finally, is the diffusion-coefficient.By rearranging the formula to isolate the diffusion-coefficient, it is possible to obtain an idea of the properties of diffusion occurring within a particular voxel
Voxel
A voxel is a volume element, representing a value on a regular grid in three dimensional space. This is analogous to a pixel, which represents 2D image data in a bitmap...
(volume picture element). These values, called apparent diffusion coefficients (ADC) can then be mapped as an image, using diffusion as the contrast.
The first successful clinical application of DWI was in imaging the brain following stroke in adults. Areas which were injured during a stroke showed up "darker" on an ADC map compared to healthy tissue. At about the same time as it became evident to researchers that DWI could be used to assess the severity of injury in adult stroke patients, they also noticed that ADC values varied depending on which way the pulse gradient was applied. This orientation-dependent contrast is generated by diffusion anisotropy, meaning that the diffusion in parts of the brain has directionality. This may be useful for determining structures in the brain which could restrict the flow of water in one direction, such as the myelinated axons of nerve cells (which is affected by multiple sclerosis). However, in imaging the brain following a stroke, it may actually prevent the injury from being seen. To compensate for this, it is necessary to apply a mathematical operator, called a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, to fully characterize the motion of water in all directions.
Diffusion-weighted images are very useful to diagnose vascular strokes in the brain. It is also used more and more in the staging of non small cell lung cancer, where it is a serious candidate to replace positron emission tomography
Positron emission tomography
Positron emission tomography is nuclear medicine imaging technique that produces a three-dimensional image or picture of functional processes in the body. The system detects pairs of gamma rays emitted indirectly by a positron-emitting radionuclide , which is introduced into the body on a...
as the 'gold standard' for this type of disease. Diffusion tensor imaging is being developed for studying the diseases of the white matter
White matter
White matter is one of the two components of the central nervous system and consists mostly of myelinated axons. White matter tissue of the freshly cut brain appears pinkish white to the naked eye because myelin is composed largely of lipid tissue veined with capillaries. Its white color is due to...
of the brain as well as for studies of other body tissues (see below).
Diffusion tensor imaging
Diffusion tensor imaging (DTI) is a magnetic resonance imagingMagnetic resonance imaging
Magnetic resonance imaging , nuclear magnetic resonance imaging , or magnetic resonance tomography is a medical imaging technique used in radiology to visualize detailed internal structures...
(MRI) technique that enables the measurement of the restricted diffusion of water in tissue in order to produce neural tract images instead of using this data solely for the purpose of assigning contrast or colors to pixels in a cross sectional image. It also provides useful structural information about muscle—including heart muscle, as well as other tissues such as the prostate.
In DTI, each voxel has one or more pairs of parameters: a rate of diffusion and a preferred direction of diffusion—described in terms of three dimensional space—for which that parameter is valid. The properties of each voxel of a single DTI image is usually calculated by vector or tensor math from six or more different diffusion weighted acquisitions, each obtained with a different orientation of the diffusion sensitizing gradients. In some methods, hundreds of measurements—each making up a complete image—are made to generate a single resulting calculated image data set. The higher information content of a DTI voxel makes it extremely sensitive to subtle pathology in the brain. In addition the directional information can be exploited at a higher level of structure to select and follow neural tracts through the brain—a process called tractography
Tractography
In neuroscience, tractography is a procedure to demonstrate the neural tracts.It uses special techniques of magnetic resonance imaging , and computer-based image analysis.The results are presented in two- and three-dimensional images....
.
A more precise statement of the image acquisition process is that the image-intensities at each position are attenuated, depending on the strength (b-value) and direction of the so-called magnetic diffusion gradient, as well as on the local microstructure in which the water molecules diffuse. The more attenuated the image is at a given position, the greater diffusion there is in the direction of the diffusion gradient. In order to measure the tissue's complete diffusion profile, one needs to repeat the MR scans, applying different directions (and possibly strengths) of the diffusion gradient for each scan.
History
In 1990, Michael Moseley reported that water diffusion in white matter was anisotropic—the effect of diffusion on proton relaxation varied depending on the orientation of tracts relative to the orientation of the diffusion gradient applied by the imaging scanner. He also pointed out that this should best be described by a tensor. Aaron Filler and colleagues reported in 1991 on the use of MRI for tract tracing in the brain using a contrast agent method but pointed out that Moseley's report on polarized water diffusion along nerves would affect the development of tract tracing. A few months after submitting that report, in 1991, the first successful use of diffusion anisotropy data to carry out the tracing of neural tracts curving through the brain without contrast agents was accomplished. Filler and colleagues identified both vector and tensor based methods in the patents in July 1992, before any other group, but the data for these initial images was obtained using the following sets of vector formulas that provide Euler anglesEuler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
and magnitude for the principal axis of diffusion in a voxel, accurately modeling the axonal directions that cause the restrictions to the direction of diffusion:
The use of mixed contributions from gradients in the three primary orthogonal axes in order to generate an infinite number of differently oriented gradients for tensor analysis was also identified in 1992 as the basis for accomplishing tensor descriptions of water diffusion in MRI voxels. Both vector and tensor methods provide a "rotationally invariant" measurement—the magnitude will be the same no matter how the tract is oriented relative to the gradient axes—and both provide a three dimensional direction in space, however the tensor method is more efficient and accurate for carrying out tractography. Practically, this class of calculated image places heavy demands on image registration—all of the images collected should ideally be identically shaped and positioned so that the calculated composite image will be correct. In the original FORTRAN program written on a MacIntosh computer by Todd Richards in late 1991, all of the tasks of image registration, and normalized anisotropy assessment (stated as a fraction of 1 and corrected for a "B0" (non-diffusion) basis), as well as calculation of the Euler angles, image generation and tract tracing were simplified by initial development with vectors (three diffusion images plus one non-diffusion image) as opposed to six or more required for a full 2nd rank tensor analysis.
The use of electromagnetic data acquisitions from six or more directions to construct a tensor ellipsoid was known from other fields at the time, as was the use of the tensor ellipsoid to describe diffusion. The inventive step of DTI therefore involved two aspects:
- the application of known methods from other fields for the generation of MRI tensor data; and
- the usable introduction of a three dimensional selective neural tract "vector graphic" concept operating at a macroscopic level above the scale of the image voxel, in a field where two dimensional pixel imaging (bit mapped graphics) had been the only method used since MRI was originated.
The abstract with the first tractogram appeared at the August 1992 meeting of the Society for Magnetic Resonance in Medicine, Widespread research in the field followed a presentation on March 28, 1993 when Michael Moseley re-presented the tractographic images from the Filler group—describing the new range of neuropathology it had made detectable—and drew attention to this new direction in MRI at a plenary session of Society for Magnetic Resonance Imaging in front of an audience of 700 MRI scientists. Many groups then paid attention to the possibility of using tensor based diffusion anisotropy imaging for neural tract tracing, beginning to optimize tractography. There is now an annual "Fibre Cup" in which various groups compete to provide the most effective new tractographic algorithm. Further advances in the development of tractography can be attributed to Mori, Pierpaoli, Lazar, Conturo and many others.
Diffusion Tensor Imaging became widely used within the MRI community following the work of Basser, Mattliello and LeBihan. Working at the National Institutes of Health, Peter Basser and his coworkers published a series of highly influential papers in the 1990s, establishing diffusion tensor imaging as a viable imaging method
. For this body of work, Basser was awarded the 2008 International Society for Magnetic Resonance in Medicine Gold Medal for "his pioneering and innovative scientific contributions in the development of Diffusion Tensor Imaging (DTI)."
Measures of anisotropy and diffusivity
In present-day clinical neurology, various brain pathologies may be best detected by looking at particular measures of anisotropy and diffusivity. The underlying physical process of diffusionDiffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
(by Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
) causes a group of water molecules to move out from a central point, and gradually reach the surface of an ellipsoid if the medium is anisotropic (it would be the surface of a sphere for an isotropic medium). The ellipsoid formalism functions also as a mathematical method of organizing tensor data. Measurement of an ellipsoid tensor further permits a retrospective analysis, to gather information about the process of diffusion in each voxel of the tissue.
In an isotropic medium such as cerebro-spinal fluid, water molecules are moving due to diffusion and they move at equal rates in all directions. By knowing the detailed effects of diffusion gradients we can generate a formula that allows us to convert the signal attenuation
Attenuation
In physics, attenuation is the gradual loss in intensity of any kind of flux through a medium. For instance, sunlight is attenuated by dark glasses, X-rays are attenuated by lead, and light and sound are attenuated by water.In electrical engineering and telecommunications, attenuation affects the...
of an MRI voxel into a numerical measure of diffusion—the diffusion coefficient D. When various barriers and restricting factors such as cell membrane
Cell membrane
The cell membrane or plasma membrane is a biological membrane that separates the interior of all cells from the outside environment. The cell membrane is selectively permeable to ions and organic molecules and controls the movement of substances in and out of cells. It basically protects the cell...
s and microtubule
Microtubule
Microtubules are a component of the cytoskeleton. These rope-like polymers of tubulin can grow as long as 25 micrometers and are highly dynamic. The outer diameter of microtubule is about 25 nm. Microtubules are important for maintaining cell structure, providing platforms for intracellular...
s interfere with the free diffusion, we are measuring an "apparent diffusion coefficient" or ADC because the measurement misses all the local effects and treats it as if all the movement rates were solely due to Brownian motion. The ADC in anisotropic tissue varies depending on the direction in which it is measured. Diffusion is fast along the length of (parallel to) an axon
Axon
An axon is a long, slender projection of a nerve cell, or neuron, that conducts electrical impulses away from the neuron's cell body or soma....
, and slower perpendicularly across it.
Once we have measured the voxel from six or more directions and corrected for attenuations due to T2 and T1 effects, we can use information from our calculated ellipsoid tensor to describe what is happening in the voxel. If you consider an ellipsoid sitting at an angle in a Cartesian
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
grid then you can consider the projection of that ellipse onto the three axes. The three projections can give you the ADC along each of the three axes ADCx, ADCy, ADCz. This leads to the idea of describing the average diffusivity in the voxel which will simply be
/3 = ADCi.
We use the i subscript to signify that this is what the isotropic diffusion coefficient would be with the effects of anisotropy averaged out.
The ellipsoid itself has a principal long axis and then two more small axes that describe its width and depth. All three of these are perpendicular to each other and cross at the center point of the ellipsoid. We call the axes in this setting eigenvectors and the measures of their lengths eigenvalues. The lengths are symbolized by the Greek letter λ
Lambda
Lambda is the 11th letter of the Greek alphabet. In the system of Greek numerals lambda has a value of 30. Lambda is related to the Phoenician letter Lamed . Letters in other alphabets that stemmed from lambda include the Roman L and the Cyrillic letter El...
. The long one pointing along the axon direction will be λ1 and the two small axes will have lengths λ2 and λ3. In the setting of the DTI tensor ellipsoid, we can consider each of these as a measure of the diffusivity along each of the three primary axes of the ellipsoid. This is a little different from the ADC since that was a projection on the axis, while λ is an actual measurement of the ellipsoid we have calculated.
The diffusivity along the principal axis, λ1 is also called the longitudinal diffusivity or the axial diffusivity or even the parallel diffusivity λ∥. Historically, this is closest to what Richards originally measured with the vector length in 1991. The diffusivities in the two minor axes are often averaged to produce a measure of radial diffusivity
/2.
This quantity is an assessment of the degree of restriction due to membranes and other effects and proves to be a sensitive measure of degenerative pathology in some neurological conditions. It can also be called the perpendicular diffusivity (λ
).Another commonly used measure that summarizes the total diffusivity is the Trace—which is the sum of the three eigenvalues,
- λ1 + λ2 + λ3.
If we divide this sum by three we have the mean diffusivity
/3.
Aside from describing the amount of diffusion, it is often important to describe the relative degree of anisotropy in a voxel. At one extreme would be the sphere of isotropic diffusion and at the other extreme would be a cigar or pencil shaped very thin prolate spheroid
Prolate spheroid
A prolate spheroid is a spheroid in which the polar axis is greater than the equatorial diameter. Prolate spheroids stand in contrast to oblate spheroids...
. The simplest measure is obtained by dividing the longest axis of the ellipsoid by the shortest = (λ1/λ3). However, this proves to be very susceptible to measurement noise, so increasingly complex measures were developed to capture the measure while minimizing the noise. An important element of these calculations is the sum of squares of the diffusivity differences = (λ1 − λ2)2 + (λ1 − λ3)2 + (λ2 − λ3)2. We use the square root of the sum of squares to obtain a sort of weighted average—dominated by the largest component. One objective is to keep the number near 0 if the voxel is spherical but near 1 if it is elongate. This leads to the fractional Anisotropy or FA which is the square root of the sum of squares (SRSS) of the diffusivity differences, divided by the SRSS of the diffusivities. When the second and third axes are small relative to the principal axis, the number in the numerator is almost equal the number in the denominator. We also multiply by the square root of 1/2 = 0.707 to help get the resulting number to be less than one. The whole formula for FA looks like this:
The fractional anisotropy can also be separated into linear, planar, and spherical measures depending on the "shape" of the diffusion ellipsoid. For example, a "cigar" shaped prolate ellipsoid indicates a strongly linear anisotropy, a "flying saucer" or oblate spheroid represents diffusion in a plane, and a sphere is indicative of isotropic diffusion, equal in all directions. If the eigenvalues of the diffusion vector are sorted such that
, then the measures can be calculated as follows:For the linear case, where
,-
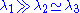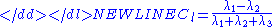
For the planar case, where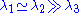
,
-
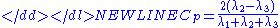
For the spherical case, where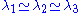
,
-
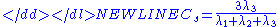
Each measure lies between 0 and 1 and they sum to unity. An additional anisotropy measure can used to describe the deviation from the spherical case:
-
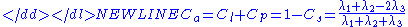
Applications
The principal application is in the imaging of white matterWhite matterWhite matter is one of the two components of the central nervous system and consists mostly of myelinated axons. White matter tissue of the freshly cut brain appears pinkish white to the naked eye because myelin is composed largely of lipid tissue veined with capillaries. Its white color is due to...
where the location, orientation, and anisotropyAnisotropyAnisotropy is the property of being directionally dependent, as opposed to isotropy, which implies identical properties in all directions. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties An example of anisotropy is the light...
of the tracts can be measured. The architecture of the axonAxonAn axon is a long, slender projection of a nerve cell, or neuron, that conducts electrical impulses away from the neuron's cell body or soma....
s in parallel bundles, and their myelinMyelinMyelin is a dielectric material that forms a layer, the myelin sheath, usually around only the axon of a neuron. It is essential for the proper functioning of the nervous system. Myelin is an outgrowth of a type of glial cell. The production of the myelin sheath is called myelination...
sheaths, facilitate the diffusionDiffusionMolecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
of the water molecules preferentially along their main direction. Such preferentially oriented diffusion is called anisotropic diffusion.
The imaging of this property is an extension of diffusion MRI. If a series of diffusion gradients (i.e. magnetic field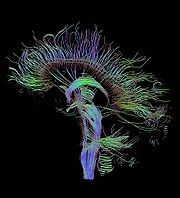
Magnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
variations in the MRI magnet) are applied that can determine at least 3 directional vectors (use of 6 different gradients is the minimum and additional gradients improve the accuracy for "off-diagonal" information), it is possible to calculate, for each voxelVoxelA voxel is a volume element, representing a value on a regular grid in three dimensional space. This is analogous to a pixel, which represents 2D image data in a bitmap...
, a tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
(i.e. a symmetric positive definite 3×3 matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
) that describes the 3-dimensional shape of diffusion. The fiber direction is indicated by the tensor's main eigenvector. This vector can be color-coded, yielding a cartography of the tracts' position and direction (red for left-right, blue for superior-inferior, and green for anterior-posterior). The brightness is weighted by the fractional anisotropy which is a scalar measure of the degree of anisotropy in a given voxel. Mean diffusivity (MD) or trace is a scalar measure of the total diffusion within a voxel. These measures are commonly used clinically to localize white matter lesions that do not show up on other forms of clinical MRI.
Diffusion tensor imaging data can be used to perform tractographyTractographyIn neuroscience, tractography is a procedure to demonstrate the neural tracts.It uses special techniques of magnetic resonance imaging , and computer-based image analysis.The results are presented in two- and three-dimensional images....
within white matter. Fiber tracking algorithms can be used to track a fiber along its whole length (e.g. the corticospinal tractCorticospinal tractThe corticospinal or pyramidal tract is a collection of axons that travel between the cerebral cortex of the brain and the spinal cord....
, through which the motor information transit from the motor cortexMotor cortexMotor cortex is a term that describes regions of the cerebral cortex involved in the planning, control, and execution of voluntary motor functions.-Anatomy of the motor cortex :The motor cortex can be divided into four main parts:...
to the spinal cordSpinal cordThe spinal cord is a long, thin, tubular bundle of nervous tissue and support cells that extends from the brain . The brain and spinal cord together make up the central nervous system...
and the peripheral nerveNerveA peripheral nerve, or simply nerve, is an enclosed, cable-like bundle of peripheral axons . A nerve provides a common pathway for the electrochemical nerve impulses that are transmitted along each of the axons. Nerves are found only in the peripheral nervous system...
s). Tractography is a useful tool for measuring deficits in white matter, such as in aging. Its estimation of fiber orientation and strength is increasingly accurate, and it has widespread potential implications in the fields of cognitive neuroscience and neurobiology.
Some clinical applications of DTI are in the tract-specific localization of white matter lesionLesionA lesion is any abnormality in the tissue of an organism , usually caused by disease or trauma. Lesion is derived from the Latin word laesio which means injury.- Types :...
s such as trauma and in defining the severity of diffuse traumatic brain injury. In one study, DTI identified blast injuries to cerebral tissue in patients who had normal appearing brains on CT and standard MRI - the study validated the imaging method while also resolving important questions about the mechanisms of diffuse axonal injuries. The localization of tumorTumorA tumor or tumour is commonly used as a synonym for a neoplasm that appears enlarged in size. Tumor is not synonymous with cancer...
s in relation to the white matter tracts (infiltration, deflection), has been one of the most important initial applications. In surgical planning for some types of brain tumors, surgery is aided by knowing the proximity and relative position of the corticospinal tractCorticospinal tractThe corticospinal or pyramidal tract is a collection of axons that travel between the cerebral cortex of the brain and the spinal cord....
and a tumor.
The use of DTI for the assessment of white matter in development, pathology and degeneration has been the focus of over 2,500 research publications since 2005. It promises to be very helpful in distinguishing Alzheimer's diseaseAlzheimer's diseaseAlzheimer's disease also known in medical literature as Alzheimer disease is the most common form of dementia. There is no cure for the disease, which worsens as it progresses, and eventually leads to death...
from other types of dementiaDementiaDementia is a serious loss of cognitive ability in a previously unimpaired person, beyond what might be expected from normal aging...
. Applications in brain research cover e.g. connectionistic investigation of neural networkNeural networkThe term neural network was traditionally used to refer to a network or circuit of biological neurons. The modern usage of the term often refers to artificial neural networks, which are composed of artificial neurons or nodes...
s in vivoIn vivoIn vivo is experimentation using a whole, living organism as opposed to a partial or dead organism, or an in vitro controlled environment. Animal testing and clinical trials are two forms of in vivo research...
.
DTI also has applications in the characterization of skeletalSkeletal muscleSkeletal muscle is a form of striated muscle tissue existing under control of the somatic nervous system- i.e. it is voluntarily controlled. It is one of three major muscle types, the others being cardiac and smooth muscle...
and cardiac muscleCardiac muscleCardiac muscle is a type of involuntary striated muscle found in the walls and histologic foundation of the heart, specifically the myocardium. Cardiac muscle is one of three major types of muscle, the others being skeletal and smooth muscle...
. The sensitivity to fiber orientation also appears to be helpful in the area of sports medicineSports medicineSports medicine is a branch of medicine that deals with physical fitness, treatment and prevention of injuries related to sports and exercise...
where it greatly aids imaging of structure and injury in muscleMuscleMuscle is a contractile tissue of animals and is derived from the mesodermal layer of embryonic germ cells. Muscle cells contain contractile filaments that move past each other and change the size of the cell. They are classified as skeletal, cardiac, or smooth muscles. Their function is to...
s and tendonTendonA tendon is a tough band of fibrous connective tissue that usually connects muscle to bone and is capable of withstanding tension. Tendons are similar to ligaments and fasciae as they are all made of collagen except that ligaments join one bone to another bone, and fasciae connect muscles to other...
s.
A recent study at Barnes-Jewish HospitalBarnes-Jewish HospitalBarnes-Jewish Hospital is the largest hospital in the U.S. state of Missouri. It is the adult teaching hospital for Washington University School of Medicine, and is located in St. Louis, Missouri. It is consistently rated one of the top hospitals in the United States by U.S. News & World Report...
and Washington University School of MedicineWashington University School of MedicineWashington University School of Medicine , located in St. Louis, Missouri, is one of the graduate schools of Washington University in St. Louis. One of the top medical schools in the United States, it is currently ranked 4th for research according to U.S. News and World Report and has been listed...
of healthy persons and both newly affected and chronically-afflicted individuals with optic neuritisOptic neuritisOptic neuritis is the inflammation of the optic nerve that may cause a complete or partial loss of vision.-Causes:The optic nerve comprises axons that emerge from the retina of the eye and carry visual information to the primary visual nuclei, most of which is relayed to the occipital cortex of the...
caused by multiple sclerosisMultiple sclerosisMultiple sclerosis is an inflammatory disease in which the fatty myelin sheaths around the axons of the brain and spinal cord are damaged, leading to demyelination and scarring as well as a broad spectrum of signs and symptoms...
(MS) showed that DTI can be used to assess the course of the condition's effects on the eye's optic nerveOptic nerveThe optic nerve, also called cranial nerve 2, transmits visual information from the retina to the brain. Derived from the embryonic retinal ganglion cell, a diverticulum located in the diencephalon, the optic nerve doesn't regenerate after transection.-Anatomy:The optic nerve is the second of...
and the vision because it can assess axial diffusivity of water flow in the area.
In October 2009 a report appeared documenting a localized increase in fractional anisotropy following training of a complex visuo-motor skill (juggling). This was claimed to be the first evidence for experience-dependent changes in white matter microstructure in healthy human adults.
Mathematical foundation—tensors
Diffusion MRI relies on the mathematics and physical interpretations of the geometric quantities known as tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s. Only a special case of the general mathematical notion is relevant to imaging, which is based on the concept of symmetric matrix. Diffusion itself is tensorial, but in many cases the objective is not really about trying to study brain diffusion per se, but rather just trying to take advantage of diffusion anisotropy in white matter for the purpose of finding the orientation of the axons and the magnitude or degree of anisotropy. Tensors have a real, physical existence in a material or tissue so that they don't move when the coordinate system used to describe them is rotated. There are numerous different possible representations of a tensor (of rank 2), but among these, this discussion focuses on the ellipsoid because of its physical relevance to diffusion and because of its historical significance in the development of diffusion anisotropy imaging in MRI.
The following matrix displays the components of the diffusion tensor:
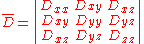
The same matrix of numbers can have a simultaneous second use to describe the shape and orientation of an ellipse and the same matrix of numbers can be used simultaneously in a third way for matrix mathematics to sort out eigenvectors and eigenvalues as explained below.
Physical tensors
The idea of a tensor in physical science evolved from attempts to describe the quantity of a given physical property. The first instances are the properties that can be described by a single number - such as temperature. There is no directionality in temperature. A property that can be described this way is denoted a scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
—it may also be considered a tensor of rank 0. The next level of complexity concerns quantities that can only be described with reference to direction—a basic example is mechanical force—these require a description of magnitude and direction. Properties with a simple directional aspect can be described by a vector—often represented by an arrow—that has magnitude and direction. A vector can be described by providing its three components—its projection on the x-axis, the y-axis and the z-axis. Vectors of this sort can be tensors of rank 1.
A tensor is often a physical or biophysical property that determines the relationship between two vectors. When a force is applied to an object, movement can result. If the movement is in a single direction—this transformation could be described using a tensor of rank 1—a vector (reporting magnitude and direction). However, in a tissue, the driving force of Brownian MotionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
will lead to movement of water molecules in an expanding pattern that proceeds along multiple different directions simultaneously, leading to a complex projection onto the Cartesian axes. This pattern is reproducible if the same conditions and forces are applied to the same tissue in the same way. If there is an internal anisotropic organization of the tissue that constrains diffusion, then this fact will be reflected in the pattern of diffusion. The relationship between the properties of driving force that generate diffusion of the water molecules and the resulting complex pattern of their movement in the tissue can be described by a tensor. The collection of molecular displacements of this physical property can be described with nine components—each one associated with a pair of axes xx, yy, zz, xy, yx, xz, zx, yz, zy. These can be written as a matrix similar to the one at the start of this section.
Diffusion from a point source in the anisotropic medium of white matter behaves in a similar fashion. The first pulse of the Stejskal Tanner diffusion gradient effectively labels some water molecules and the second pulse effectively shows their displacement due to diffusion. Each gradient direction applied measures the movement along the direction of that gradient. Six or more gradients are summated to get all the measurements needed to fill in the matrix —assuming it is symmetric above and below the diagonal (red subscripts).
In 1848, Henri Hureau de SénarmontHenri Hureau de SénarmontHenri Hureau de Sénarmont was a French mineralogist and physician. He was born at Brou, Eure-et-Loir. In the course of his career, he became engineer-in-chief of mines, and professor of mineralogy and director of studies at the École des Mines at Paris.Sénarmont was distinguished for his research...
applied a heated point to a polished crystal surface that had been coated with wax. In some materials that had "isotropic" structure, a ring of melt would spread across the surface in a circle. In anisotropic crystals the spread took the form of an ellipse. In three dimensions this spread is an ellipsoid. As Adolf FickAdolf Eugen FickAdolf Eugen Fick was a German physiologist. He started to study mathematics and physics, but then realized he was more interested in medicine. He earned his doctorate in medicine at Marburg in 1851...
showed in the 1850s diffusion follows many of the same paths and rules as does heat.
Mathematics of ellipsoids
At this point, it is helpful to consider the mathematics of ellipsoids. An ellipsoid can be described by the formula: ax2 + by2 + cz2 = 1. A great way to gain further intuition is to download "Graphing Calculator" from nucalc.com. This equation describes a quadricQuadricIn mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
surface. The relative values of a, b, and c determine if the quadric describes an ellipsoid or a hyperboloid.
As it turns out, three more components can be added as follows:
ax2 + by2 + cz2 + dyz + ezx + fxy = 1. Many combinations of a, b, c, d, e, and f still describe ellipsoids, but the additional components (d, e, f) describe the rotation of the ellipsoid relative to the orthogonal axes of the Cartesian coordinate system. These six variables can be represented by a matrix similar to the tensor matrix defined at the start of this section (since diffusion is symmetric, then we only need six instead of nine components—the components below the diagonal elements of the matrix are the same as the components above the diagonal). This is what is meant when it is stated that the components of a matrix of a second order tensor can be represented by an ellipsoid—if the diffusion values of the six terms of the quadric ellipsoid are placed into the matrix, this generates an ellipsoid angled off the orthogonal grid. Its shape will be more elongated if the relative anisotropy is high.
When the ellipsoid/tensor is represented by a matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, we can apply a useful technique from standard matrix mathematics and linear algebra—that is to "diagonalize" the matrix. This has two important meanings in imaging. The idea is that there are two equivalent ellipsoids—of identical shape but with different size and orientation. The first one is the measured diffusion ellipsoid sitting at an angle determined by the axons, and the second one is perfectly aligned with the three CartesianCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
axes. The term "diagonalize" refers to the three components of the matrix along a diagonal from upper left to lower right (the components with red subscripts in the matrix at the start of this section). The variables ax2, by2, and cz2 are along the diagonal (red subscripts), but the variables d, e and f are "off diagonal". It then becomes possible to do a vector processing step in which we rewrite our matrix and replace it with a new matrix multiplied by three different vectors of unit length (length=1.0). The matrix is diagonalized because the off-diagonal components are all now zero. The rotation angles required to get to this equivalent position now appear in the three vectors and can be read out as the x, y, and z components of each of them. Those three vectors are called "eigenvectors" or characteristic vectors. They contain the orientation information of the original ellipsoid. The three axes of the ellipsoid are now directly along the main orthogonal axes of the coordinate system so we can easily infer their lengths. These lengths are the eigenvalues or characteristic values.
DiagonalizationDiagonalizable matrixIn linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
of a matrix is done by finding a second matrix that it can be multiplied with followed by multiplication by the inverse of the second matrix—wherein the result is a new matrix in which three diagonal (xx, yy, zz) components have numbers in them but the off-diagonal components (xy, yz, zx) are 0. The second matrix provides eigenvector information.
HARDI: High-angular-resolution diffusion imaging and Q-ball vector analysis
Early in the development of DTI based tractography, a number of researchers pointed out a flaw in the diffusion tensor model. The tensor analysis assumes that there is a single ellipsoid in each imaging voxel—as if all of the axons traveling through a voxel traveled in exactly the same direction. This is often true, but it can be estimated that in more than 30% of the voxels in a standard resolution brain image, there are at least two different neural tracts traveling in different directions that pass through each other. In the classic diffusion ellipsoid tensor model, the information from the crossing tract just appears as noise or unexplained decreased anisotropy in a given voxel. David Tuch was among the first to describe a working solution to this problem.
The idea is best understood by conceptually placing a kind of geodesic dome around each image voxel. This icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
provides a mathematical basis for passing a large number of evenly spaced gradient trajectories through the voxel—each coinciding with one of the apices of the icosahedron. Basically, we are now going to look into the voxel from a large number of different directions (typically 40 or more). We use "n-tuple" tessellations to add more evenly spaced apices to the original icosahedron (20 faces)—an idea that also had its precedents in paleomagnetism research several decades earlier. We just want to know which direction lines turn up the maximum anisotropic diffusion measures. If there is a single tract, there will be just two maxima pointing in opposite directions. If two tracts cross in the voxel, there will be two pairs of maxima, and so on. We can still use tensor math to use the maxima to select groups of gradients to package into several different tensor ellipsoids in the same voxel, or use more complex higher rank tensors analyses, or we can do a true "model free" analysis that just picks the maxima and goes on about doing the tractography. We could use very high angular resolution (256 different directions) but it is often necessary to do ten or fifteen complete runs to get the information correct and this could mean 2,000 or more images—it gets to be over an hour to do the image and so becomes impossible. At forty angles, we can do 10 repetitions and get done in ten minutes. Also, in order to make this work, the gradient strengths have to be considerably higher than for standard DTI. This is because we can reduce the apparent noise (non-diffusion contributions to signal) at higher b values (a combination of gradient strength and pulse duration) and improve the spatial resolution.
The Q-Ball method of tractography is an implementation of the HARDI approach in which David Tuch provides a mathematical alternative to the tensor model. Instead of forcing the diffusion anisotropy data into a group of tensors, the mathematics used deploys both probability distributions and a classic bit of geometric tomographyTomographyTomography refers to imaging by sections or sectioning, through the use of any kind of penetrating wave. A device used in tomography is called a tomograph, while the image produced is a tomogram. The method is used in radiology, archaeology, biology, geophysics, oceanography, materials science,...
and vector math developed nearly 100 years ago—the Funk Radon Transform.
Summary
For DTI, it is generally possible to use linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, matrix mathematics and vector mathematics to process the analysis of the tensor data.
In some cases, the full set of tensor properties is of interest, but for tractographyTractographyIn neuroscience, tractography is a procedure to demonstrate the neural tracts.It uses special techniques of magnetic resonance imaging , and computer-based image analysis.The results are presented in two- and three-dimensional images....
it is usually necessary to know only the magnitude and orientation of the primary axis or vector. This primary axis—the one with the greatest length—is the largest eigenvalue and its orientation is encoded in its matched eigenvector. Only one axis is needed because the interest is in the vectorial property of axon direction to accomplish tractography.
See also
- fDTI
- Camino (diffusion MRI toolkit)
- ConnectomeConnectomeA connectome is a comprehensive map of neural connections in the brain.The production and study of connectomes, known as connectomics, may range in scale from a detailed map of the full set of neurons and synapses within part or all of the nervous system of an organism to a macro scale description...
- Dipy: Diffusion Imaging in Python
External links
-
-
-