Gauss's lemma (polynomial)
Encyclopedia
In algebra
, in the theory of polynomial
s (a subfield of ring theory
), Gauss's lemma is either of two related statements about polynomials with integer coefficients:
This second statement is a consequence of the first (see proof below). The first statement and proof of the lemma is in Article 42 of Carl Friedrich Gauss
's Disquisitiones Arithmeticae
(1801).
in the context of finite fields) is defined in any polynomial ring R[X] where R is an integral domain: a polynomial P in R[X] is primitive if the only elements of R that divide all coefficients of P at once are the invertible elements of R. In the case where R is the ring Z of the integers, this is equivalent to the condition that no prime number
divides all the coefficients of P. The notion of irreducible element
is defined in any integral domain: an element is irreducible if it is not invertible and cannot be written as a product of two non-invertible elements. In the case of a polynomial ring R[X], this means that a non-constant irreducible polynomial is one that is not a product of two non-constant polynomials and which is primitive (because being primitive excludes precisely non-invertible constant polynomials as factors). Note that an irreducible element of R is still irreducible when viewed as constant polynomial in R[X]; this explains the need for "non-constant" above, and in the irreducibility statements below.
The two properties of polynomials with integer coefficients can now be formulated formally as follows:
These statements can be generalized to any unique factorization domain
(UFD), where they become
The condition that R is a UFD is not superfluous. In a ring where factorization is not unique, say pa = qb with p and q irreducible elements that do not divide any of the factors on the other side, the product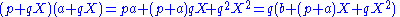
shows the failure of the primitivity statement. For a concrete example one can take
In this example the polynomial (obtained by dividing the right hand side by ) provides an example of the failure of the irreducibility statement (it is irreducible over R, but reducible over its field of fractions ). Another well known example is the polynomial , whose roots are the golden ratio
and its conjugate 
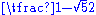, showing that it is reducible over the field , although it is irreducible over the non-UFD which has as field of fractions. In the latter example the ring can be made into an UFD by taking its integral closure in (the ring of Dirichlet integers), over which becomes reducible, but in the former example R is already integrally closed.
Proof: Suppose the product of two primitive polynomials f(x) and g(x) is not primitive, so there exists a prime number p that is a common divisor of all the coefficients of the product. But since f(x) and g(x) are primitive, p cannot divide either all the coefficients of f(x) or all those of g(x). Let arxr and bsxs be the first (i.e., highest degree) terms respectively of f(x) and of g(x) with a coefficient not divisible by p. Now consider the coefficient of xr+s in the product. Its value is given by
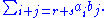
This sum contains a term arbs which is not divisible by p (because p is prime, by Euclid's lemma
), yet all the remaining ones are (because either or ), so the entire sum is not divisible by p. But by assumption all coefficients in the product are divisible by p, leading to a contradiction. Therefore, the coefficients of the product can have no common divisor and are thus primitive. This completes the proof.
A cleaner version of this proof can be given using the statement from abstract algebra
that a polynomial ring
over an integral domain is again an integral domain. We formulate this proof directly for the case of polynomials over a UFD R, which is hardly different from its special case for R = Z.
Proof: Let S,T be primitive polynomials in R[X], and assume that their product ST is not primitive, so that some non invertible element d of R divides all coefficients of ST. There is some irreducible element
p of R that divides d, and it is also a prime element
in R (since R is a UFD). Then the principal ideal
pR generated by p is a prime ideal
, so R/pR is an integral domain, and (R/pR)[X] is therefore an integral domain as well. By hypothesis the projection R[X]→(R/pR)[X] sends ST to 0, and also at least one of S,T individually, which means that p divides all of its coefficients, contradicting primitivity.
The somewhat tedious bookkeeping in the first proof is simplified by the fact that the reduction modulo p kills the uninteresting terms; what is left is a proof that polynomials over an integral domain cannot be zero divisor
s by consideration of the leading coefficient of their product.
, and in particular of a principal ideal domain
). Call a polynomial P in R[X] co-maximal if the ideal of R generated by the coefficients of the polynomial is full ring R (when R is a UFD that is not a PID, then co-maximality is much more restrictive than primitivity). The variation of Gauss's lemma says: the product of two co-maximal polynomials is co-maximal.
Proof:
Let S,T be co-maximal polynomials in R[X], and assume that their product ST is not co-maximal. Then its coefficients generate a proper ideal I, which by Krull's theorem
(which depends on the axiom of choice) is contained in a maximal ideal
m of R.Then R/m is a field, and (R/m)[X] is therefore an integral domain. By hypothesis the projection R[X]→(R/m)[X] sends ST to 0, and also at least one of S,T individually, which means that its coefficients all lie in m, which contradicts the fact that they generate the whole ring as an ideal.
s. There the contents of a polynomial can be defined as the greatest common divisor
of the coefficients of (like the gcd, the contents is actually a class of associate elements). The primitivity statement can be generalized to the statement that the contents of a product of polynomials is the product of their contents; in fact this is equivalent to the primitivity statement since is certainly a common divisor of the coefficients of the product, so one can divide by and to reduce and to primitive polynomials. However the proof given above cannot be used when is a GCD domain, since it uses irreducible factors, which need not exist in such . Here is a proof that is valid in this context.
We proceed by induction on the total number of nonzero terms of and combined. If one of the polynomials has at most one term, the result is obvious; this covers in particular all cases with fewer than 4 nonzero terms. So let both and have at least 2 terms, and assume the result established for any smaller combined number of terms. By dividing by and by , we reduce to the case . If the contents is not invertible, it has a non-trivial divisor in common with the leading coefficient of at least one of and (since it divides their product, which is the leading coefficient of ). Suppose by symmetry that this is the case for , let be the leading term of , and let be the mentioned common divisor (here the contents of is just its unique coefficient). Since is a common divisor of and , it also divides , in other words it divides its contents, which by induction (since has fewer terms than ) is . As also divides , it divides , which gives a contradiction; therefore is invertible (and can be taken to be 1).
Note first that in F[X]\{0} any class of associate elements (whose elements are related by multiplication by nonzero elements of the field F) meets the set of primitive elements in R[X]: starting from an arbitrary element of the class, one can first (if necessary) multiply by a nonzero element of R to enter into the subset R[X] (removing denominators), then divide by the greatest common divisor of all coefficients to obtain a primitive polynomial. Now assume that P is reducible in F[X], so with S,T non-constant polynomials in F[X]. One can replace S and T by associate primitive elements S′, T′, and obtain for some nonzero α in F. But S′T′ is primitive in R[X] by the primitivity statement, so α must lie in R (if written as an irreducible fraction
, its denominator has to divide all coefficients of S′T′ because αS′T′ lies in R[X], but that means the denominator is invertible in R), and the decomposition contradicts the irreducibility of P in R[X].
The second result implies that if a polynomial with integer coefficients can be factored over the rational numbers, then there exists a factorization over the integers. This property is also useful when combined with properties such as Eisenstein's criterion
.
Both results are essential in proving that if R is a unique factorization domain, then so is R[X] (and by an immediate induction, so is the polynomial ring
over R in any number of indeterminates). For any factorization of a polynomial P in R[X], the statements imply that the product Q of all irreducible factors that are not contained in R (the non-constant factors) is always primitive, so P = c(P)Q where c(P) is the contents of P. This reduces proving uniqueness of factorizations to proving it individually for c(P) (which is given) and for Q. By the second statement the irreducible factors in any factorization of Q in R[X] are primitive representatives of irreducible factors in a factorization of Q in F[X], but the latter is unique since F[X] is a principal ideal domain
and therefore a unique factorization domain.
The second result also implies that the minimal polynomial
over the rational numbers of an algebraic integer
has integer coefficients.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, in the theory of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s (a subfield of ring theory
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
), Gauss's lemma is either of two related statements about polynomials with integer coefficients:
- The first result states that the product of two primitive polynomials is primitive (a polynomial with integer coefficients is called primitive if the greatest common divisor of its coefficientsContent (algebra)In algebra, the content of a polynomial is the highest common factor of its coefficients.A polynomial is primitive if it has content unity....
is 1). - The second result states that if a polynomial with integer coefficientCoefficientIn mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s is irreducibleIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over the integers, then it is also irreducible if it is considered as a polynomial over the rationalsRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
.
This second statement is a consequence of the first (see proof below). The first statement and proof of the lemma is in Article 42 of Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
's Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
(1801).
Formal statements
The notion of primitive polynomial used here (which differs from the notion with the same namePrimitive polynomial
In field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite extension field GF...
in the context of finite fields) is defined in any polynomial ring R[X] where R is an integral domain: a polynomial P in R[X] is primitive if the only elements of R that divide all coefficients of P at once are the invertible elements of R. In the case where R is the ring Z of the integers, this is equivalent to the condition that no prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
divides all the coefficients of P. The notion of irreducible element
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
is defined in any integral domain: an element is irreducible if it is not invertible and cannot be written as a product of two non-invertible elements. In the case of a polynomial ring R[X], this means that a non-constant irreducible polynomial is one that is not a product of two non-constant polynomials and which is primitive (because being primitive excludes precisely non-invertible constant polynomials as factors). Note that an irreducible element of R is still irreducible when viewed as constant polynomial in R[X]; this explains the need for "non-constant" above, and in the irreducibility statements below.
The two properties of polynomials with integer coefficients can now be formulated formally as follows:
- Primitivity statement: The set of primitive polynomials in Z[X] is closedClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under multiplication: if P and Q are primitive polynomials then so is their product PQ.
- Irreducibility statement: A non-constant polynomial in Z[X] is irreducible in Z[X] if and only if it is both irreducible in Q[X] and primitive in Z[X].
These statements can be generalized to any unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
(UFD), where they become
- Primitivity statement: If R is a UFD, then the set of primitive polynomials in R[X] is closed under multiplication.
- Irreducibility statement: Let R be a UFD and F its field of fractionsField of fractionsIn abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
. A non-constant polynomial in R[X] is irreducible in R[X] if and only if it is both irreducible in F[X] and primitive in R[X].
The condition that R is a UFD is not superfluous. In a ring where factorization is not unique, say pa = qb with p and q irreducible elements that do not divide any of the factors on the other side, the product
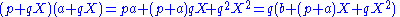
shows the failure of the primitivity statement. For a concrete example one can take
In this example the polynomial (obtained by dividing the right hand side by ) provides an example of the failure of the irreducibility statement (it is irreducible over R, but reducible over its field of fractions ). Another well known example is the polynomial , whose roots are the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
and its conjugate 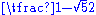, showing that it is reducible over the field , although it is irreducible over the non-UFD which has as field of fractions. In the latter example the ring can be made into an UFD by taking its integral closure in (the ring of Dirichlet integers), over which becomes reducible, but in the former example R is already integrally closed.Proofs of the primitivity statement
An elementary proof of the statement that the product of primitive polynomials over Z is again primitive can be given as follows.Proof: Suppose the product of two primitive polynomials f(x) and g(x) is not primitive, so there exists a prime number p that is a common divisor of all the coefficients of the product. But since f(x) and g(x) are primitive, p cannot divide either all the coefficients of f(x) or all those of g(x). Let arxr and bsxs be the first (i.e., highest degree) terms respectively of f(x) and of g(x) with a coefficient not divisible by p. Now consider the coefficient of xr+s in the product. Its value is given by
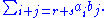
This sum contains a term arbs which is not divisible by p (because p is prime, by Euclid's lemma
Euclid's lemma
In mathematics, Euclid's lemma is an important lemma regarding divisibility and prime numbers. In its simplest form, the lemma states that a prime number that divides a product of two integers must divide one of the two integers...
), yet all the remaining ones are (because either or ), so the entire sum is not divisible by p. But by assumption all coefficients in the product are divisible by p, leading to a contradiction. Therefore, the coefficients of the product can have no common divisor and are thus primitive. This completes the proof.
A cleaner version of this proof can be given using the statement from abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
that a polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
over an integral domain is again an integral domain. We formulate this proof directly for the case of polynomials over a UFD R, which is hardly different from its special case for R = Z.
Proof: Let S,T be primitive polynomials in R[X], and assume that their product ST is not primitive, so that some non invertible element d of R divides all coefficients of ST. There is some irreducible element
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
p of R that divides d, and it is also a prime element
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
in R (since R is a UFD). Then the principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
pR generated by p is a prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
, so R/pR is an integral domain, and (R/pR)[X] is therefore an integral domain as well. By hypothesis the projection R[X]→(R/pR)[X] sends ST to 0, and also at least one of S,T individually, which means that p divides all of its coefficients, contradicting primitivity.
The somewhat tedious bookkeeping in the first proof is simplified by the fact that the reduction modulo p kills the uninteresting terms; what is left is a proof that polynomials over an integral domain cannot be zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s by consideration of the leading coefficient of their product.
A variation, valid over arbitrary commutative rings
Gauss's lemma is not valid over general integral domains. However there is a variation of Gauss's lemma that is valid even for polynomials over any commutative ring R, which replaces primitivity by the stronger property of co-maximality (which is however equivalent to primitivity in the case of a Bézout domainBézout domain
In mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
, and in particular of a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
). Call a polynomial P in R[X] co-maximal if the ideal of R generated by the coefficients of the polynomial is full ring R (when R is a UFD that is not a PID, then co-maximality is much more restrictive than primitivity). The variation of Gauss's lemma says: the product of two co-maximal polynomials is co-maximal.
Proof:
Let S,T be co-maximal polynomials in R[X], and assume that their product ST is not co-maximal. Then its coefficients generate a proper ideal I, which by Krull's theorem
Krull's theorem
In mathematics, more specifically in ring theory, Krull's theorem, named after Wolfgang Krull, proves the existence of maximal ideals in any unital ring. The theorem was first stated in 1929 and is equivalent to the axiom of choice.- Krull's theorem :...
(which depends on the axiom of choice) is contained in a maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
m of R.Then R/m is a field, and (R/m)[X] is therefore an integral domain. By hypothesis the projection R[X]→(R/m)[X] sends ST to 0, and also at least one of S,T individually, which means that its coefficients all lie in m, which contradicts the fact that they generate the whole ring as an ideal.
A proof valid over any GCD domain
Gauss's lemma holds over arbitrary GCD domainGCD domain
In mathematics, a GCD domain is an integral domain R with the property that any two non-zero elements have a greatest common divisor . Equivalently, any two non-zero elements of R have a least common multiple ....
s. There the contents of a polynomial can be defined as the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of the coefficients of (like the gcd, the contents is actually a class of associate elements). The primitivity statement can be generalized to the statement that the contents of a product of polynomials is the product of their contents; in fact this is equivalent to the primitivity statement since is certainly a common divisor of the coefficients of the product, so one can divide by and to reduce and to primitive polynomials. However the proof given above cannot be used when is a GCD domain, since it uses irreducible factors, which need not exist in such . Here is a proof that is valid in this context.
We proceed by induction on the total number of nonzero terms of and combined. If one of the polynomials has at most one term, the result is obvious; this covers in particular all cases with fewer than 4 nonzero terms. So let both and have at least 2 terms, and assume the result established for any smaller combined number of terms. By dividing by and by , we reduce to the case . If the contents is not invertible, it has a non-trivial divisor in common with the leading coefficient of at least one of and (since it divides their product, which is the leading coefficient of ). Suppose by symmetry that this is the case for , let be the leading term of , and let be the mentioned common divisor (here the contents of is just its unique coefficient). Since is a common divisor of and , it also divides , in other words it divides its contents, which by induction (since has fewer terms than ) is . As also divides , it divides , which gives a contradiction; therefore is invertible (and can be taken to be 1).
Proof of the irreducibility statement
We prove the irreducibility statement directly in the setting of a UFD R. As mentioned above a non-constant polynomial is irreducible in R[X] if and only if it is primitive and not a product of two non-constant polynomials in R[X]. Being irreducible in F[X] certainly excludes the latter possibility (since those non-constant polynomials would remain non-invertible in F[X]), so the essential point left to prove is that if P is non-constant and irreducible in R[X] then it is irreducible in F[X].Note first that in F[X]\{0} any class of associate elements (whose elements are related by multiplication by nonzero elements of the field F) meets the set of primitive elements in R[X]: starting from an arbitrary element of the class, one can first (if necessary) multiply by a nonzero element of R to enter into the subset R[X] (removing denominators), then divide by the greatest common divisor of all coefficients to obtain a primitive polynomial. Now assume that P is reducible in F[X], so with S,T non-constant polynomials in F[X]. One can replace S and T by associate primitive elements S′, T′, and obtain for some nonzero α in F. But S′T′ is primitive in R[X] by the primitivity statement, so α must lie in R (if written as an irreducible fraction
Irreducible fraction
An irreducible fraction is a vulgar fraction in which the numerator and denominator are smaller than those in any other equivalent vulgar fraction...
, its denominator has to divide all coefficients of S′T′ because αS′T′ lies in R[X], but that means the denominator is invertible in R), and the decomposition contradicts the irreducibility of P in R[X].
Implications
The first result implies that the contents of polynomials, defined as the GCD of their coefficients, are multiplicative: the contents of the product of two polynomials is the product of their individual contents.The second result implies that if a polynomial with integer coefficients can be factored over the rational numbers, then there exists a factorization over the integers. This property is also useful when combined with properties such as Eisenstein's criterion
Eisenstein's criterion
In mathematics, Eisenstein's criterion gives an easily checked sufficient condition for a polynomial with integer coefficients to be irreducible over the rational numbers...
.
Both results are essential in proving that if R is a unique factorization domain, then so is R[X] (and by an immediate induction, so is the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
over R in any number of indeterminates). For any factorization of a polynomial P in R[X], the statements imply that the product Q of all irreducible factors that are not contained in R (the non-constant factors) is always primitive, so P = c(P)Q where c(P) is the contents of P. This reduces proving uniqueness of factorizations to proving it individually for c(P) (which is given) and for Q. By the second statement the irreducible factors in any factorization of Q in R[X] are primitive representatives of irreducible factors in a factorization of Q in F[X], but the latter is unique since F[X] is a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
and therefore a unique factorization domain.
The second result also implies that the minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
over the rational numbers of an algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
has integer coefficients.