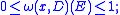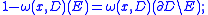Harmonic measure
Encyclopedia
In mathematics
, especially potential theory
, harmonic measure is a concept related to the theory of harmonic function
s that arises from the solution of the classical Dirichlet problem
. In probability theory
, harmonic measure of a bounded domain in Euclidean space
 ,
,  is the probability that a Brownian motion
is the probability that a Brownian motion
started inside a domain hits a portion of the boundary. More generally, harmonic measure of an Itō diffusion
X describes the distribution of X as it hits the boundary of D. In the complex plane
, harmonic measure can be used to estimate the modulus
of an analytic function
inside a domain D given bounds on the modulus on the boundary
of the domain; a special case of this principle is Hadamard's Three-circle theorem
. On simply connected planar domains, there is a close connection between harmonic measure and the theory of conformal map
s.
The term harmonic measure was introduced by R. Nevanlinna in 1934 for planar domains, although Nevanlinna notes the idea appeared implicitly in earlier work by Johansson, F. Riesz, M. Riesz, Carleman, Ostrowski and Julia (original order cited). The connection between harmonic measure and Brownian motion was first identified by Kakutani ten years later in 1944
, open domain
in n-dimension
al Euclidean space
Rn, n ≥ 2, and let ∂D denote the boundary of D. Any continuous function
f : ∂D → R determines a unique harmonic function
Hf that solves the Dirichlet problem

If a point x ∈ D is fixed, by the Riesz representation theorem
and the maximum principle
Hf(x) determines a probability measure
ω(x, D) on ∂D by
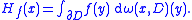
The measure ω(x, D) is called the harmonic measure (of the domain D with pole at x).
Since explicit formulas for harmonic measure are not typically available, we are interested in determining conditions which guarantee a set has harmonic measure zero.
starting at 0 exits the interval
(−1, +1) at −1 with probability ½ and at +1 with probability ½, so Bτ(−1, +1) is uniformly distributed on the set {−1, +1}.
In general, if G is compactly embedded
within Rn, then the harmonic measure (or hitting distribution) of X on the boundary ∂G of G is the measure μGx defined by
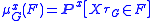
for x ∈ G and F ⊆ ∂G.
Returning to the earlier example of Brownian motion, one can show that if B is a Brownian motion in Rn starting at x ∈ Rn and D ⊂ Rn is an open ball centred on x, then the harmonic measure of B on ∂D is invariant
under all rotation
s of D about x and coincides with the normalized surface measure on ∂D
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
, harmonic measure is a concept related to the theory of harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s that arises from the solution of the classical Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
. In probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, harmonic measure of a bounded domain in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
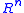 ,
,  is the probability that a Brownian motion
is the probability that a Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
started inside a domain hits a portion of the boundary. More generally, harmonic measure of an Itō diffusion
Ito diffusion
In mathematics — specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation, used in Physics to describe the brownian motion of a particle subjected to a potential in a...
X describes the distribution of X as it hits the boundary of D. In the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, harmonic measure can be used to estimate the modulus
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
inside a domain D given bounds on the modulus on the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the domain; a special case of this principle is Hadamard's Three-circle theorem
Hadamard three-circle theorem
In complex analysis, a branch of mathematics, theHadamard three-circle theorem is a result about the behavior of holomorphic functions.Let f be a holomorphic function on the annulusr_1\leq\left| z\right| \leq r_3....
. On simply connected planar domains, there is a close connection between harmonic measure and the theory of conformal map
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
s.
The term harmonic measure was introduced by R. Nevanlinna in 1934 for planar domains, although Nevanlinna notes the idea appeared implicitly in earlier work by Johansson, F. Riesz, M. Riesz, Carleman, Ostrowski and Julia (original order cited). The connection between harmonic measure and Brownian motion was first identified by Kakutani ten years later in 1944
Definition
Let D be a boundedBounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
, open domain
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, n ≥ 2, and let ∂D denote the boundary of D. Any continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
f : ∂D → R determines a unique harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
Hf that solves the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....

If a point x ∈ D is fixed, by the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
and the maximum principle
Maximum principle
In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
Hf(x) determines a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
ω(x, D) on ∂D by
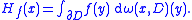
The measure ω(x, D) is called the harmonic measure (of the domain D with pole at x).
Properties
- For any Borel subset E of ∂D, the harmonic measure ω(x, D)(E) is equal to the value at x of the solution to the Dirichlet problem with boundary data equal to the indicator function of E.
- For fixed D and E ⊆ ∂D, ω(x, D)(E) is an harmonic function of x ∈ D and
- Hence, for each x and D, ω(x, D) is a probability measureProbability measureIn mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on ∂D.
- If ω(x, D)(E) = 0 at even a single point x of D, then y
 ω(y, D)(E) is identically zero, in which case E is said to be a set of harmonic measure zero. This is a consequence of Harnack's inequalityHarnack's inequalityIn mathematics, Harnack's inequality is an inequality relating the values of a positive harmonic function at two points, introduced by . and generalized Harnack's inequality to solutions of elliptic or parabolic partial differential equations. Perelman's solution of the Poincaré conjecture uses...
ω(y, D)(E) is identically zero, in which case E is said to be a set of harmonic measure zero. This is a consequence of Harnack's inequalityHarnack's inequalityIn mathematics, Harnack's inequality is an inequality relating the values of a positive harmonic function at two points, introduced by . and generalized Harnack's inequality to solutions of elliptic or parabolic partial differential equations. Perelman's solution of the Poincaré conjecture uses...
.
Since explicit formulas for harmonic measure are not typically available, we are interested in determining conditions which guarantee a set has harmonic measure zero.
- F. and M. Riesz Theorem: If
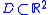 is a simply connected planar domain bounded by a rectifiable curveArc lengthDetermining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
is a simply connected planar domain bounded by a rectifiable curveArc lengthDetermining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
(i.e. if ), then harmonic measure is mutually absolutely continuous with respect to arc length: for all
), then harmonic measure is mutually absolutely continuous with respect to arc length: for all 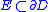 ,
, 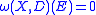 if and only if
if and only if 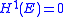 .
.
- Makarov's theorem: Let
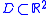 be a simply connected planar domain. If
be a simply connected planar domain. If  and
and 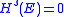 for some
for some  , then
, then 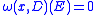 . Moreover, harmonic measure on D is mutually singularSingular measureIn mathematics, two positive measures μ and ν defined on a measurable space are called singular if there exist two disjoint sets A and B in Σ whose union is Ω such that μ is zero on all measurable subsets of B while ν is zero on all measurable subsets of A...
. Moreover, harmonic measure on D is mutually singularSingular measureIn mathematics, two positive measures μ and ν defined on a measurable space are called singular if there exist two disjoint sets A and B in Σ whose union is Ω such that μ is zero on all measurable subsets of B while ν is zero on all measurable subsets of A...
with respect to t-dimensional Hausdorff measure for all t>1.
- Dahlberg's theorem: If
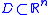 is a bounded Lipschitz domainLipschitz domainIn mathematics, a Lipschitz domain is a domain in Euclidean space whose boundary is "sufficiently regular" in the sense that it can be thought of as locally being the graph of a Lipschitz continuous function...
is a bounded Lipschitz domainLipschitz domainIn mathematics, a Lipschitz domain is a domain in Euclidean space whose boundary is "sufficiently regular" in the sense that it can be thought of as locally being the graph of a Lipschitz continuous function...
, then harmonic measure and (n-1)-dimensional Hausdorff measure are mutually absolutely continuous: for all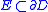 ,
,  if and only if
if and only if 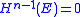 .
.
Examples
- If
 is the unit disk, then harmonic measure of
is the unit disk, then harmonic measure of  with pole at the origin is length measure on the unit circle normalized to be a probability, i.e.
with pole at the origin is length measure on the unit circle normalized to be a probability, i.e. 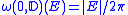 for all
for all  where
where  denotes the length of
denotes the length of  .
.
- If
 is the unit disk and
is the unit disk and 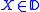 , then
, then 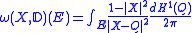 for all
for all 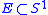 where
where 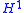 denotes length measure on the unit circle. The Radon-Nikodym derivative
denotes length measure on the unit circle. The Radon-Nikodym derivative 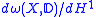 is called the Poisson kernelPoisson kernelIn potential theory, the Poisson kernel is an integral kernel, used for solving the two-dimensional Laplace equation, given Dirichlet boundary conditions on the unit disc. The kernel can be understood as the derivative of the Green's function for the Laplace equation...
is called the Poisson kernelPoisson kernelIn potential theory, the Poisson kernel is an integral kernel, used for solving the two-dimensional Laplace equation, given Dirichlet boundary conditions on the unit disc. The kernel can be understood as the derivative of the Green's function for the Laplace equation...
.
- More generally, if
 and
and 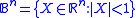 is the n-dimensional unit ball, then harmonic measure with pole at
is the n-dimensional unit ball, then harmonic measure with pole at 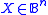 is
is 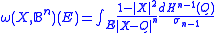 for all
for all 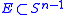 where
where  denotes surface measure (
denotes surface measure ( -dimensional Hausdorff measureHausdorff measureIn mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
-dimensional Hausdorff measureHausdorff measureIn mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
) on the unit sphere and
and 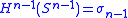 .
.
- If
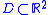 is a simply connected planar domain bounded by a Jordan curve and X
is a simply connected planar domain bounded by a Jordan curve and X D, then
D, then 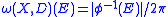 for all
for all 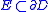 where
where 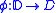 is the unique Riemann map which sends the origin to X, i.e.
is the unique Riemann map which sends the origin to X, i.e. 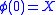 . See Carathéodory's theoremCarathéodory's theorem (conformal mapping)In mathematical complex analysis, Carathéodory's theorem, proved by , states that if U is a simply connected open subset of the complex plane C, whose boundary is a Jordan curve Γ then the Riemann map...
. See Carathéodory's theoremCarathéodory's theorem (conformal mapping)In mathematical complex analysis, Carathéodory's theorem, proved by , states that if U is a simply connected open subset of the complex plane C, whose boundary is a Jordan curve Γ then the Riemann map...
.
- If
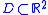 is the domain bounded by the Koch snowflakeKoch snowflakeThe Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
is the domain bounded by the Koch snowflakeKoch snowflakeThe Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
, then there exists a subset of the Koch snowflake such that
of the Koch snowflake such that  has zero length (
has zero length (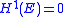 ) and full harmonic measure
) and full harmonic measure 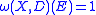 .
.
The harmonic measure of a diffusion
Consider an Rn-valued Itō diffusion X starting at some point x in the interior of a domain D, with law Px. Suppose that one wishes to know the distribution of the points at which X exits D. For example, canonical Brownian motion B on the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
starting at 0 exits the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
(−1, +1) at −1 with probability ½ and at +1 with probability ½, so Bτ(−1, +1) is uniformly distributed on the set {−1, +1}.
In general, if G is compactly embedded
Compactly embedded
In mathematics, the notion of being compactly embedded expresses the idea that one set or space is "well contained" inside another. There are versions of this concept appropriate to general topology and functional analysis.-Definition :...
within Rn, then the harmonic measure (or hitting distribution) of X on the boundary ∂G of G is the measure μGx defined by
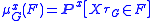
for x ∈ G and F ⊆ ∂G.
Returning to the earlier example of Brownian motion, one can show that if B is a Brownian motion in Rn starting at x ∈ Rn and D ⊂ Rn is an open ball centred on x, then the harmonic measure of B on ∂D is invariant
Invariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
under all rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s of D about x and coincides with the normalized surface measure on ∂D