Isomonodromic deformation
Encyclopedia
In mathematics
, the equations governing the isomonodromic deformation of meromorphic linear systems of ordinary differential equations are, in a fairly precise sense, the most fundamental exact nonlinear differential equations. As a result, their solutions and properties lie at the heart of the field of exact nonlinearity and integrable systems.
Isomonodromic deformations were first studied by Richard Fuchs
, with early pioneering contributions from Paul Painlevé
, René Garnier, and Ludwig Schlesinger
. Inspired by results in statistical mechanics
, a seminal contribution to the theory was made by Michio Jimbo
, Tetsuji Miwa and Kimio Ueno, who studied cases with arbitrary singularity structure.
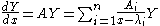
where the dependent variable
takes values in the complex projective line 
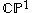, the solution 
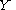takes values in 
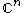and the 
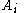are constant 
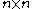matrices. By placing 
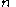independent column solutions into a fundamental matrix
we can regard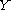
as taking values in 
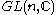. Solutions to this equation have simple poles at 
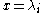. For simplicity, we shall assume that there is no further pole at infinity (which amounts to the condition that 
).
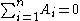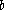on the Riemann sphere away from the poles. Analytic continuation
of the solution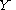
around any pole 
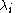and back to the basepoint will produce a new solution 
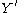. The new and old solutions are linked by the monodromy
matrix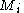
as follows: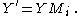
We therefore have the Riemann–Hilbert homomorphism
from the fundamental group
of the punctured sphere to the monodromy representation: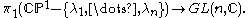
A change of basepoint merely results in a (simultaneous) conjugation of all the monodromy matrices. The monodromy matrices modulo simultaneous conjugation define the monodromy data of the Fuchsian system.
. We do not distinguish between coordinates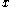
and 
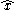which are related by Möbius transformations, and we do not distinguish between gauge equivalent Fuchsian systems - this means that we regard 
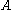and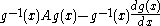
as being equivalent for any holomorphic gauge transformation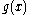
. (It is thus most natural to regard a Fuchsian system geometrically, as a connection
with simple poles on a trivial rank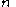
vector bundle
over the Riemann sphere).
For generic monodromy data, the answer to Hilbert's twenty-first problem is 'yes' - as was first proved by Josip Plemelj
. However, Plemelj neglected certain degenerate cases, and it was shown in 1989 by Andrei Bolibrukh that there are cases when the answer is 'no'. Here, we focus entirely on the generic case.
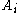to depend on the positions of the poles.
In 1912 (following earlier incorrect attempts) Ludwig Schlesinger
proved that in general, the deformations which preserve the monodromy data of a (generic) Fuchsian system are governed by the integrable holonomic
system of partial differential equations which now bear his name:
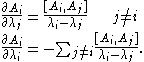
These are therefore the isomonodromy equations for (generic) Fuchsian systems. It should be noted that the natural interpretation of these equations is as the flatness of a natural connection on a vector bundle over the 'deformation parameter space' which consists of the possible pole positions. For non-generic isomonodromic deformations, there will still be an integrable isomonodromy equation, but it will no longer be Schlesinger.
If we limit ourselves to the case when the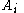
take values in the Lie algebra 
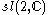, we obtain the so-called Garnier systems.
If we specialize further to the case when there are only four poles, then the Schlesinger/Garnier equations can be reduced to the famous sixth Painlevé equation.
in correlation functions in the theory of Bose gases, Michio Jimbo, Tetsuji Miwa and Kimio Ueno extended the notion of isomonodromic deformation to the case of arbitrary pole structure. The linear system we study is now of the form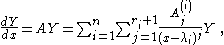
with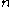
poles, with the pole at 
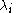of order 
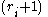. The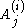 
are constant matrices.
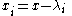as a local coordinate near a pole 
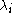of order
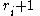, then we can solve term-by-term for a holomorphic gauge transformation 
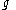such that locally, the system looks like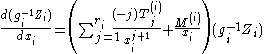
where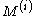
and the 
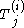are diagonal matrices. If this were valid, it would be extremely useful, because then (at least locally), we have decoupled the system into 
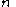scalar differential equations which we can easily solve to find that (locally):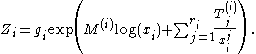
However, this does not work - because the power series we have solved term-for-term for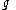
will not, in general, converge.
It was the great insight of Jimbo, Miwa and Ueno to realize that nevertheless, this approach provides canonical solutions near the singularities, and can therefore be gainfully employed to define extended monodromy data. This is because of a theorem of George Birkhoff which states that given such a formal series, there is a unique convergent function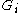
such that in any particular sufficiently large sector around the pole, 
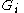is asymptotic to 
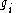, and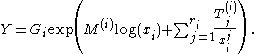
is a true solution of the differential equation. We therefore have a canonical solution in each such sector near each pole. The extended monodromy data consists of
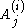to depend on parameters. We allow ourselves to vary the positions of the poles 
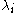, but now, in addition, we also vary the entries of the diagonal matrices 
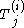which appear in the canonical solution near each pole.
Jimbo, Miwa and Ueno proved that if we define a one-form on the 'deformation parameter space' by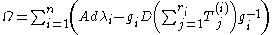
(where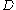
denotes exterior differentiation with respect to the components of the 
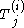only)
then deformations of the meromorphic linear system specified by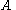
are isomonodromic if and only if
These are the general isomonodromy equations. As before, these equations can be interpreted as the flatness of a natural connection on the deformation parameter space.
.
for the case of Fuchsian systems, and by Tetsuji Miwa in the general setting.
Indeed, suppose we are given a partial differential equation (or a system of them). Then, 'possessing a reduction to an isomonodromy equation' is more or less equivalent to the
Painlevé property, and can therefore be used as a test for integrability
.
' by Hiroshi Umemura and Bernard Malgrange
.
There are also very special solutions which are algebraic
. The study of such algebraic solutions involves examining the topology
of the deformation parameter space (and in particular, its mapping class group
); for the case of simple poles, this amounts to the study of the action of braid groups. For the particularly important case of the sixth Painlevé equation, there has been a notable contribution by Boris Dubrovin and Marta Mazzocco, which has been recently extended to larger classes of monodromy data by Philip Boalch.
Rational solutions are often associated to special polynomials. Sometimes, as in the case of the sixth Painlevé equation, these are well-known orthogonal polynomials
, but there are new classes of polynomials with extremely interesting distribution of zeros and interlacing properties. The study of such polynomials has largely been carried out by Peter Clarkson and collaborators.
formulations. This viewpoint was extensively pursued by Kazuo Okamoto in a series of papers on the Painlevé equations in the 1980s.
They can also be regarding as a natural extension of the Atiyah-Bott symplectic structure on spaces of flat connections on Riemann surfaces to the world of meromorphic geometry - a perspective pursued by Philip Boalch. Indeed, if we fix the positions of the poles, we can even obtain complete hyperkähler manifolds; a result proved by Oliver Biquard and Philip Boalch.
There is another description in terms of moment maps to (central extensions of) loop algebras - a viewpoint introduced by John Harnad
and extended to the case of general singularity structure by Nick Woodhouse. This latter perspective is intimately related to a curious Laplace transform between isomonodromy equations with different pole structure and rank for the underlying equations.
in studying the properties of transcendents. This approach has been pursued by Nigel Hitchin
, Lionel Mason and Nick Woodhouse.
and others.
The initial impetus for the resurgence of interest in isomonodromy in the 1970s was the appearance of transcendents in correlation functions in Bose gases.
They provide generating functions for moduli spaces of two-dimensional topological quantum field theories and are thereby useful in the study of quantum cohomology
and Gromov-Witten invariants.
'Higher-order' isomonodromy equations have recently been used to explain the mechanism and universality properties of shock formation for the dispersionless limit of the Korteweg–de Vries equation
.
They are natural reductions of the Ernst equation
and thereby provide solutions to the Einstein equations of general relativity; they also give rise to other (quite distinct) solutions of the Einstein equations in terms of theta functions.
They have arisen in recent work in mirror symmetry
- both in the geometric Langlands programme, and in work on the moduli spaces of stability conditions on derived categories.
.
They can also easily be adapted to take values in any Lie group
, by replacing the diagonal matrices by the maximal torus
, and other similar modifications.
There is a burgeoning field studying discrete versions of isomonodromy equations.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the equations governing the isomonodromic deformation of meromorphic linear systems of ordinary differential equations are, in a fairly precise sense, the most fundamental exact nonlinear differential equations. As a result, their solutions and properties lie at the heart of the field of exact nonlinearity and integrable systems.
Isomonodromic deformations were first studied by Richard Fuchs
Richard Fuchs
Richard Fuchs, composer and architect, was born in Karlsruhe, Baden, Germany, on 26 April 1887 and died in Wellington, New Zealand, on 22 September 1947. The football player Gottfried Fuchs was his younger brother....
, with early pioneering contributions from Paul Painlevé
Paul Painlevé
Paul Painlevé was a French mathematician and politician. He served twice as Prime Minister of the Third Republic: 12 September – 13 November 1917 and 17 April – 22 November 1925.-Early life:Painlevé was born in Paris....
, René Garnier, and Ludwig Schlesinger
Ludwig Schlesinger
Ludwig Schlesinger was a German mathematician known for the research in the field of linear differential equations.-Biography:...
. Inspired by results in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, a seminal contribution to the theory was made by Michio Jimbo
Michio Jimbo
is a Japanese mathematician, currently a professor at the University of Tokyo. He is a grandson of the linguist Kaku Jimbo.After graduating from the University of Tokyo in 1974, he studied under Mikio Sato at the Research Institute for Mathematical Sciences in Kyoto University...
, Tetsuji Miwa and Kimio Ueno, who studied cases with arbitrary singularity structure.
Fuchsian systems and Schlesinger's equations
We consider the Fuchsian system of linear differential equations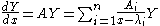where the dependent variable
takes values in the complex projective line 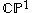, the solution 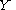takes values in 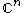and the 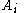are constant 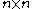matrices. By placing 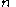independent column solutions into a fundamental matrixFundamental matrix
A fundamental matrix may refer to* fundamental matrix * fundamental matrix...
we can regard
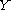as taking values in 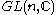. Solutions to this equation have simple poles at 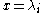. For simplicity, we shall assume that there is no further pole at infinity (which amounts to the condition that 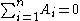).Monodromy data
Now, fix a basepoint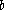 on the Riemann sphere away from the poles. Analytic continuationAnalytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of the solution
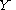around any pole 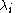and back to the basepoint will produce a new solution 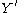. The new and old solutions are linked by the monodromyMonodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
matrix
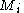as follows: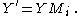We therefore have the Riemann–Hilbert homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the punctured sphere to the monodromy representation:
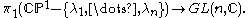
A change of basepoint merely results in a (simultaneous) conjugation of all the monodromy matrices. The monodromy matrices modulo simultaneous conjugation define the monodromy data of the Fuchsian system.
Hilbert's twenty-first problem
Now, with given monodromy data, can we find a Fuchsian system which exhibits this monodromy? This is one form of Hilbert's twenty-first problemHilbert's twenty-first problem
The twenty-first problem of the 23 Hilbert problems, from the celebrated list put forth in 1900 by David Hilbert, was phrased like this ....
. We do not distinguish between coordinates
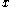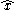and which are related by Möbius transformations, and we do not distinguish between gauge equivalent Fuchsian systems - this means that we regar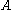d and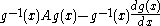as being equivalent for any holomorphic gauge transformation
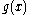. (It is thus most natural to regard a Fuchsian system geometrically, as a connectionConnection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
with simple poles on a trivial rank
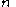vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over the Riemann sphere).
For generic monodromy data, the answer to Hilbert's twenty-first problem is 'yes' - as was first proved by Josip Plemelj
Josip Plemelj
Josip Plemelj was a Slovene mathematician, whose main contributions were to the theory of analytic functions and the application of integral equations to potential theory.- Life :...
. However, Plemelj neglected certain degenerate cases, and it was shown in 1989 by Andrei Bolibrukh that there are cases when the answer is 'no'. Here, we focus entirely on the generic case.
Schlesinger's equations
There are (generically) many Fuchsian systems with the same monodromy data. Thus, given any such Fuchsian system with specified monodromy data, we can perform isomonodromic deformations of it. We are therefore led to study families of Fuchsian systems, and allow the matrices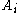 to depend on the positions of the poles.In 1912 (following earlier incorrect attempts) Ludwig Schlesinger
Ludwig Schlesinger
Ludwig Schlesinger was a German mathematician known for the research in the field of linear differential equations.-Biography:...
proved that in general, the deformations which preserve the monodromy data of a (generic) Fuchsian system are governed by the integrable holonomic
Holonomic
In mathematics and physics, the term holonomic may occur with several different meanings.-Holonomic basis:A holonomic basis for a manifold is a set of basis vectors ek for which all Lie derivatives vanish:[e_j,e_k]=0 \,...
system of partial differential equations which now bear his name:
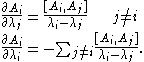
These are therefore the isomonodromy equations for (generic) Fuchsian systems. It should be noted that the natural interpretation of these equations is as the flatness of a natural connection on a vector bundle over the 'deformation parameter space' which consists of the possible pole positions. For non-generic isomonodromic deformations, there will still be an integrable isomonodromy equation, but it will no longer be Schlesinger.
If we limit ourselves to the case when the
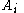take values in the Lie algebra 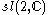, we obtain the so-called Garnier systems.If we specialize further to the case when there are only four poles, then the Schlesinger/Garnier equations can be reduced to the famous sixth Painlevé equation.
Irregular singularities
Motivated by the appearance of Painlevé transcendentsPainlevé transcendents
In mathematics, Painlevé transcendents are solutions to certain nonlinear second-order ordinary differential equations in the complex plane with the Painlevé property , but which are not generally solvable in terms of elementary functions...
in correlation functions in the theory of Bose gases, Michio Jimbo, Tetsuji Miwa and Kimio Ueno extended the notion of isomonodromic deformation to the case of arbitrary pole structure. The linear system we study is now of the form
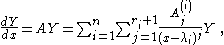
with
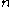poles, with the pole at 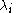of order 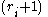. The 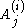are constant matrices.Extended monodromy data
As well as the monodromy representation described in the Fuchsian setting, deformations of irregular systems of linear ordinary differential equations are required to preserve extended monodromy data. Roughly speaking, monodromy data is now regarded as data which glues together canonical solutions near the singularities. If we take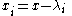 as a local coordinate near a pole 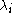of orderDegree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
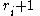, then we can solve term-by-term for a holomorphic gauge transformation 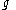such that locally, the system looks like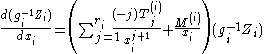where
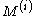and the 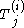are diagonal matrices. If this were valid, it would be extremely useful, because then (at least locally), we have decoupled the system into 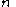scalar differential equations which we can easily solve to find that (locally):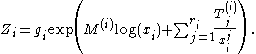However, this does not work - because the power series we have solved term-for-term for
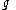will not, in general, converge.It was the great insight of Jimbo, Miwa and Ueno to realize that nevertheless, this approach provides canonical solutions near the singularities, and can therefore be gainfully employed to define extended monodromy data. This is because of a theorem of George Birkhoff which states that given such a formal series, there is a unique convergent function
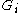such that in any particular sufficiently large sector around the pole, 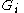is asymptotic to 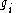, and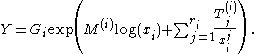is a true solution of the differential equation. We therefore have a canonical solution in each such sector near each pole. The extended monodromy data consists of
- the data from the monodromy representation as for the Fuchsian case;
- Stokes' matrices which connect canonical solutions between adjacent sectors at the same pole;
- connection matrices which connect canonical solutions between sectors at different poles.
General isomonodromic deformations
As before, we now consider families of systems of linear differential equations, all with the same singularity structure. We therefore allow the matrices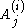 to depend on parameters. We allow ourselves to vary the positions of the poles 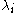, but now, in addition, we also vary the entries of the diagonal matrices 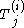which appear in the canonical solution near each pole.Jimbo, Miwa and Ueno proved that if we define a one-form on the 'deformation parameter space' by
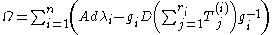
(where
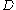denotes exterior differentiation with respect to the components of the 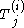only)then deformations of the meromorphic linear system specified by
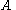are isomonodromic if and only ifThese are the general isomonodromy equations. As before, these equations can be interpreted as the flatness of a natural connection on the deformation parameter space.
Properties
The isomonodromy equations enjoy a number of properties which justify their status as nonlinear special functionsSpecial functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
.
Painlevé property
This is perhaps the most important property of a solution to the isomonodromic deformation equations. This means that all essential singularities of the solutions are fixed, although the positions of poles may move. It was proved by Bernard MalgrangeBernard Malgrange
Bernard Malgrange is a French mathematician who works on differential equations and singularity theory.He proved the Ehrenpreis–Malgrange theorem and the Malgrange preparation theorem....
for the case of Fuchsian systems, and by Tetsuji Miwa in the general setting.
Indeed, suppose we are given a partial differential equation (or a system of them). Then, 'possessing a reduction to an isomonodromy equation' is more or less equivalent to the
Painlevé property, and can therefore be used as a test for integrability
Integrability
Integrability may refer to:* Riemann integrability; see Riemann integral* Lebesgue integrability; see Lebesgue integral* Darboux integrability; see Darboux integral* System integration * Interoperability...
.
Transcendence
In general, solutions of the isomonodromy equations cannot be expressed in terms of simpler functions such as solutions of linear differential equations. However, for particular (more precisely, reducible) choices of extended monodromy data, solutions can be expressed in terms of such functions (or at least, in terms of 'simpler' isomonodromy transcendents). The study of precisely what this transcendence means has been largely carried out by the invention of 'nonlinear differential Galois theoryDifferential Galois theory
In mathematics, differential Galois theory studies the Galois groups of differential equations.Whereas algebraic Galois theory studies extensions of algebraic fields, differential Galois theory studies extensions of differential fields, i.e. fields that are equipped with a derivation, D. Much of...
' by Hiroshi Umemura and Bernard Malgrange
Bernard Malgrange
Bernard Malgrange is a French mathematician who works on differential equations and singularity theory.He proved the Ehrenpreis–Malgrange theorem and the Malgrange preparation theorem....
.
There are also very special solutions which are algebraic
Algebraic
Algebraic may refer to any subject within the algebra branch of mathematics and related branches like algebraic geometry and algebraic topology.Algebraic may also refer to:...
. The study of such algebraic solutions involves examining the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of the deformation parameter space (and in particular, its mapping class group
Mapping class group
In mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
); for the case of simple poles, this amounts to the study of the action of braid groups. For the particularly important case of the sixth Painlevé equation, there has been a notable contribution by Boris Dubrovin and Marta Mazzocco, which has been recently extended to larger classes of monodromy data by Philip Boalch.
Rational solutions are often associated to special polynomials. Sometimes, as in the case of the sixth Painlevé equation, these are well-known orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
, but there are new classes of polynomials with extremely interesting distribution of zeros and interlacing properties. The study of such polynomials has largely been carried out by Peter Clarkson and collaborators.
Symplectic structure
The isomonodromy equations can be rewritten using HamiltonianHamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
formulations. This viewpoint was extensively pursued by Kazuo Okamoto in a series of papers on the Painlevé equations in the 1980s.
They can also be regarding as a natural extension of the Atiyah-Bott symplectic structure on spaces of flat connections on Riemann surfaces to the world of meromorphic geometry - a perspective pursued by Philip Boalch. Indeed, if we fix the positions of the poles, we can even obtain complete hyperkähler manifolds; a result proved by Oliver Biquard and Philip Boalch.
There is another description in terms of moment maps to (central extensions of) loop algebras - a viewpoint introduced by John Harnad
John Harnad
John Harnad is a Hungarian-born mathematical physicist. He did his undergraduate work at McGill University and his graduate work at the University of Oxford...
and extended to the case of general singularity structure by Nick Woodhouse. This latter perspective is intimately related to a curious Laplace transform between isomonodromy equations with different pole structure and rank for the underlying equations.
Twistor structure
The isomonodromy equations arise as (generic) full dimensional reductions of (generalized) anti-self-dual Yang-Mills equations. By the Penrose-Ward transform they can therefore be interpreted in terms of holomorphic vector bundles on complex manifolds called twistor spaces. This allows the use of powerful techniques from algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
in studying the properties of transcendents. This approach has been pursued by Nigel Hitchin
Nigel Hitchin
Nigel Hitchin is a British mathematician working in the fields of differential geometry, algebraic geometry, and mathematical physics.-Academic career:...
, Lionel Mason and Nick Woodhouse.
Gauss-Manin connections
By considering data associated with families of Riemann surfaces branched over the singularities, we can consider the isomonodromy equations as nonhomogenous Gauss-Manin connections. This leads to alternative descriptions of the isomonodromy equations in terms of abelian functions - an approach known to Fuchs and Painlevé, but lost until rediscovery by Yuri Manin in 1996.Asymptotics
Particular transcendents can be characterized by their asymptotic behaviour. The study of such behaviour goes back to the early days of isomonodromy, in work by Pierre BoutrouxPierre Boutroux
Pierre Léon Boutroux was a French mathematician and historian of science. Boutroux is chiefly known for his work in the history and philosophy of mathematics.-Biography:...
and others.
Applications
Their universality as the simplest genuinely nonlinear integrable systems means that the isomonodromy equations have an extremely diverse range of applications. Perhaps of greatest practical importance is the field of random matrix theory. Here, the statistical properties of eigenvalues of large random matrices are described by particular transcendents.The initial impetus for the resurgence of interest in isomonodromy in the 1970s was the appearance of transcendents in correlation functions in Bose gases.
They provide generating functions for moduli spaces of two-dimensional topological quantum field theories and are thereby useful in the study of quantum cohomology
Quantum cohomology
In mathematics, specifically in symplectic topology and algebraic geometry, a quantum cohomology ring is an extension of the ordinary cohomology ring of a closed symplectic manifold. It comes in two versions, called small and big; in general, the latter is more complicated and contains more...
and Gromov-Witten invariants.
'Higher-order' isomonodromy equations have recently been used to explain the mechanism and universality properties of shock formation for the dispersionless limit of the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
.
They are natural reductions of the Ernst equation
Ernst equation
In mathematics, the Ernst equation is the non-linear partial differential equation\displaystyle \Re = ^2+^2.It is used to produce exact solutions of Einstein's equations....
and thereby provide solutions to the Einstein equations of general relativity; they also give rise to other (quite distinct) solutions of the Einstein equations in terms of theta functions.
They have arisen in recent work in mirror symmetry
Mirror symmetry
In physics and mathematics, mirror symmetry is a relation that can exist between two Calabi-Yau manifolds. It happens, usually for two such six-dimensional manifolds, that the shapes may look very different geometrically, but nevertheless they are equivalent if they are employed as hidden...
- both in the geometric Langlands programme, and in work on the moduli spaces of stability conditions on derived categories.
Generalizations
The isomonodromy equations have been generalized for meromorphic connections on a general Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
.
They can also easily be adapted to take values in any Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, by replacing the diagonal matrices by the maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
, and other similar modifications.
There is a burgeoning field studying discrete versions of isomonodromy equations.