Music and mathematics - AbsoluteAstronomy.com

Music
Music
Music is an art form whose medium is sound and silence. Its common elements are pitch , rhythm , dynamics, and the sonic qualities of timbre and texture...

theorists often use mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

to understand music. Indeed, mathematics is "the basis of sound" and sound itself "in its musical aspects... exhibits a remarkable array of number properties", simply because nature itself "is amazingly mathematical". Though ancient Chinese, Egyptians and Mesopotamians are known to have studied the mathematical principles of sound, the Pythagoreans

Pythagoreanism

Pythagoreanism was the system of esoteric and metaphysical beliefs held by Pythagoras and his followers, the Pythagoreans, who were considerably influenced by mathematics. Pythagoreanism originated in the 5th century BCE and greatly influenced Platonism...

of ancient Greece are the first researchers known to have investigated the expression of musical scale

Musical scale

In music, a scale is a sequence of musical notes in ascending and descending order. Most commonly, especially in the context of the common practice period, the notes of a scale will belong to a single key, thus providing material for or being used to conveniently represent part or all of a musical...

s in terms of numerical ratio

Ratio

In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...

s, particularly the ratios of small integers. Their central doctrine was that "all nature consists of harmony
Harmony
In music, harmony is the use of simultaneous pitches , or chords. The study of harmony involves chords and their construction and chord progressions and the principles of connection that govern them. Harmony is often said to refer to the "vertical" aspect of music, as distinguished from melodic...

arising out of numbers".

From the time of Plato

Plato

Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...

, harmony was considered a fundamental branch of physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, now known as musical acoustics

Musical acoustics

Musical acoustics or music acoustics is the branch of acoustics concerned with researching and describing the physics of music – how sounds employed as music work...

. Early Indian and Chinese

Chinese musicology

Chinese musicology is the academic study of traditional Chinese music. This discipline has a very long history. The concept of music yue stands among the oldest categories of Chinese thought, however, in the known sources it does not receive more or less clear definition until the Book of Music...

theorists show similar approaches: all sought to show that the mathematical laws of harmonic

Harmonic

A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...

s and rhythm

Rhythm

Rhythm may be generally defined as a "movement marked by the regulated succession of strong and weak elements, or of opposite or different conditions." This general meaning of regular recurrence or pattern in time may be applied to a wide variety of cyclical natural phenomena having a periodicity or...

s were fundamental not only to our understanding of the world but to human well-being. Confucius

Confucius

Confucius , literally "Master Kong", was a Chinese thinker and social philosopher of the Spring and Autumn Period....

, like Pythagoras, regarded the small numbers 1,2,3,4 as the source of all perfection.

To this day mathematics has more to do with acoustics than with composition, and the use of mathematics in composition is historically limited to the simplest operations of counting and measuring. The attempt to structure and communicate new ways of composing and hearing music has led to musical applications of set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

, abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

and number theory

Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

. Some composers have incorporated the Golden ratio

Golden ratio

In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...

and Fibonacci numbers into their work.

Time, rhythm and meter

Without the boundaries of rhythmic structure – a fundamental equal and regular arrangement of pulse
Pulse (music)
In music and music theory, the pulse or tactus consists of beats in a series of identical yet distinct periodic short-duration stimuli perceived as points in time occurring at the mensural level...

repetitivity, accent
Beat (music)
The beat is the basic unit of time in music, the pulse of the mensural level . In popular use, the beat can refer to a variety of related concepts including: tempo, meter, rhythm and groove...

, phrase
Phrase (music)
In music and music theory, phrase and phrasing are concepts and practices related to grouping consecutive melodic notes, both in their composition and performance...

and duration – music would be impossible. In Old English the word "rhyme", derived from "rhythm", became associated and confused with rim - "number" - and modern musical use of terms like metre
Metre (music)
Meter or metre is a term that music has inherited from the rhythmic element of poetry where it means the number of lines in a verse, the number of syllables in each line and the arrangement of those syllables as long or short, accented or unaccented...

and measure also reflects the historical importance of music, along with astronomy, in the development of counting, arithmetic and the exact measurement of time and periodicity

Frequency

Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...

that is fundamental to physics.

Musical form

Musical form is the plan by which a short piece of music is extended. The term "plan" is also used in architecture, to which musical form is often compared. Like the architect, the composer must take into account the function for which the work is intended and the means available, practising economy and making use of repetition and order. The common types of form known as binary
Binary form
Binary form is a musical form in two related sections, both of which are usually repeated. Binary is also a structure used to choreograph dance....

and ternary
Ternary form
Ternary form, sometimes called song form, is a three-part musical form, usually schematicized as A-B-A. The first and third parts are musically identical, or very nearly so, while the second part in some way provides a contrast with them...

("twofold" and "threefold") once again demonstrate the importance of small integral values to the intelligibility and appeal of music.

Frequency and harmony

A musical scale

Musical scale

is a discrete set of pitch

Pitch (music)

Pitch is an auditory perceptual property that allows the ordering of sounds on a frequency-related scale.Pitches are compared as "higher" and "lower" in the sense associated with musical melodies,...

es used in making or describing music. The most important scale in the Western tradition is the diatonic scale

Diatonic scale

In music theory, a diatonic scale is a seven note, octave-repeating musical scale comprising five whole steps and two half steps for each octave, in which the two half steps are separated from each other by either two or three whole steps...

but many others have been used and proposed in various historical eras and parts of the world. Each pitch corresponds to a particular frequency, expressed in hertz (Hz), sometimes referred to as cycles per second (c.p.s.). A scale has an interval of repetition, normally the octave

Octave

In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...

. The octave

Octave

of any pitch refers to a frequency exactly twice that of the given pitch. Succeeding superoctaves are pitches found at frequencies four, eight, sixteen times, and so on, of the fundamental frequency. Pitches at frequencies of half, a quarter, an eighth and so on of the fundamental are called suboctaves. There is no case in musical harmony where, if a given pitch be considered accordant, that its octaves are considered otherwise. Therefore any note and its octaves will generally be found similarly named in musical systems (e.g. all will be called doh or A or Sa, as the case may be). When expressed as a frequency bandwidth an octave A-A spans from 110 Hz to 220 Hz (span=110 Hz). The next octave will span from 220 Hz to 440 Hz (span=220 Hz). The third octave spans from 440 Hz to 880 Hz (span=440 Hz) and so on. Each successive octave spans twice the frequency range of the previous octave.

Because we are often interested in the relations or ratio

Ratio

s between the pitches (known as intervals

Interval (music)

In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...

) rather than the precise pitches themselves in describing a scale, it is usual to refer all the scale pitches in terms of their ratio from a particular pitch, which is given the value of one (often written 1/1), generally a note which functions as the tonic

Tonic (music)

In music, the tonic is the first scale degree of the diatonic scale and the tonal center or final resolution tone. The triad formed on the tonic note, the tonic chord, is thus the most significant chord...

of the scale. For interval size comparison cent

Cent (music)

The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...

s are often used.

Common name	name	Ratio within octave
Fundamental	A₂,	1/1 = 1x
Octave	A₃	2/1 = 2x
Octave	A₃	2/2 = 1x
Perfect Fifth	E₃	3/2 = 1.5x
Octave	A₄	4/2 = 2x
Octave	A₄	4/4 = 1x
Major Third	C₄	5/4 = 1.25x
Perfect Fifth	E₄	6/4 = 1.5x
Harmonic seventh Harmonic seventh The harmonic seventh interval , also known as the septimal minor seventh, or subminor seventh, is one with an exact 7:4 ratio . This is somewhat narrower than and is "sweeter in quality" than an "ordinary" minor seventh, which has a just-intonation ratio of 9:5 , or an equal-temperament ratio of...	G₄	7/4 = 1.75x
Octave	A₅	8/4 = 2x
Octave	A₅	8/8 = 1x

Tuning systems

5-limit tuning, the most common form of Just intonation

Just intonation

In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...

, is a system of tuning using tones that are regular number

Regular number

Regular numbers are numbers that evenly divide powers of 60. As an example, 602 = 3600 = 48 × 75, so both 48 and 75 are divisors of a power of 60...

harmonic

Harmonic

s of a single fundamental frequency

Fundamental frequency

The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the lowest frequency of a periodic waveform. In terms of a superposition of sinusoids The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the...

. This was one of the scales Johannes Kepler

Johannes Kepler

Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...

presented in his Harmonice Mundi

Harmonice Mundi

Harmonices Mundi is a book by Johannes Kepler. In the work Kepler discusses harmony and congruence in geometrical forms and physical phenomena...

(1619) in connection with planetary motion. The same scale was given in transposed form by Alexander Malcolm

Alexander Malcolm

Alexander Scott Malcolm was an independent conservative and then Reform Party Member of Parliament in New Zealand.He was elected to the Clutha electorate in the 1905 general election, but was defeated in 1922. He was later on the Legislative Council, from 1924 to 1931.-References:*New Zealand...

in 1721 and by theorist Jose Wuerschmidt in the 20th century. A form of it is used in the music of northern India. American composer Terry Riley

Terry Riley

Terrence Mitchell Riley, is an American composer intrinsically associated with the minimalist school of Western classical music and was a pioneer of the movement...

also made use of the inverted form of it in his "Harp of New Albion". Just intonation gives superior results when there is little or no chord progression

Chord progression

A chord progression is a series of musical chords, or chord changes that "aims for a definite goal" of establishing a tonality founded on a key, root or tonic chord. In other words, the succession of root relationships...

: voices and other instruments gravitate to just intonation whenever possible. However, as it gives two different whole tone intervals (9:8 and 10:9) a keyboard instrument so tuned cannot change key. To calculate the frequency of a note in a scale given in terms of ratios, the frequency ratio is multiplied by the tonic frequency. For instance, with a tonic of A4 (A natural above middle C), the frequency is 440 Hz

Hertz

The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....

, and a justly tuned fifth above it (E5) is simply 440*(3:2) = 660 Hz.

Note	Ratio	Interval Interval (music) In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
0	1:1	unison Unison In music, the word unison can be applied in more than one way. In general terms, it may refer to two notes sounding the same pitch, often but not always at the same time; or to the same musical voice being sounded by several voices or instruments together, either at the same pitch or at a distance...
1	16:15	major semitone Semitone A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
2	9:8	major second Major second In Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions...
3	6:5	minor third Minor third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major...
4	5:4	major third Major third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
5	4:3	perfect fourth Perfect fourth In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
6	45:32	diatonic tritone Tritone In classical music from Western culture, the tritone \|tone]]) is traditionally defined as a musical interval composed of three whole tones. In a chromatic scale, each whole tone can be further divided into two semitones...
7	3:2	perfect fifth Perfect fifth In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
8	8:5	minor sixth Minor sixth -Subminor sixth:In music, a subminor sixth or septimal sixth is an interval that is noticeably narrower than a minor sixth but noticeably wider than a diminished sixth.The sub-minor sixth is an interval of a 14:9 ratio or alternately 11:7....
9	5:3	major sixth Major sixth In classical music from Western culture, a sixth is a musical interval encompassing six staff positions , and the major sixth is one of two commonly occurring sixths. It is qualified as major because it is the largest of the two...
10	9:5	minor seventh Minor seventh In classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the minor seventh is one of two commonly occurring sevenths. The minor quality specification identifies it as being the smallest of the two: the minor seventh spans ten semitones, the...
11	15:8	major seventh Major seventh In classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the major seventh is one of two commonly occurring sevenths. It is qualified as major because it is the larger of the two...
12	2:1	octave Octave In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...

Pythagorean tuning

Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...

is tuning based only on the perfect consonances, the (perfect) octave, perfect fifth, and perfect fourth. Thus the major third is considered not a third but a ditone, literally "two tones", and is 81:64 = (9:8)², rather than the independent and harmonic just 5:4, directly below. A whole tone is a secondary interval, being derived from two perfect fifths, (3:2)^2 = 9:8.

The just major third, 5:4 and minor third, 6:5, are a syntonic comma

Syntonic comma

In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...

, 81:80, apart from their Pythagorean equivalents 81:64 and 32:27 respectively. According to Carl Dahlhaus

Carl Dahlhaus

Carl Dahlhaus , a musicologist from Berlin, was one of the major contributors to the development of musicology as a scholarly discipline during the post-war era....

(1990, p. 187), "the dependent third conforms to the Pythagorean, the independent third to the harmonic tuning of intervals."

Western common practice music

Common practice period

The common practice period, in the history of Western art music , spanning the Baroque, Classical, and Romantic periods, lasted from c. 1600 to c. 1900.-General characteristics:...

usually cannot be played in just intonation but requires a systematically tempered scale. The tempering can involve either the irregularities of well temperament

Well temperament

Well temperament is a type of tempered tuning described in 20th-century music theory. The term is modelled on the German word wohltemperiert which appears in the title of J.S. Bach's famous composition, The Well-Tempered Clavier...

or be constructed as a regular temperament

Regular temperament

Regular temperament is any tempered system of musical tuning such that each frequency ratio is obtainable as a product of powers of a finite number of generators, or generating frequency ratios...

, either some form of equal temperament

Equal temperament

An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...

or some other regular meantone, but in all cases will involve the fundamental features of meantone temperament

Meantone temperament

Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...

. For example, the root of chord ii, if tuned to a fifth above the dominant, would be a major whole tone (9:8) above the tonic. If tuned a just minor third (6:5) below a just subdominant degree of 4:3, however, the interval from the tonic would equal a minor whole tone (10:9) Meantone temperament reduces the difference between 9:8 and 10:9. Their ratio, (9:8)/(10:9) = 81:80, is treated as a unison. The interval 81:80, called the syntonic comma

Syntonic comma

or comma of Didymus, is the key comma of meantone temperament.

In equal temperament

Equal temperament

, the octave is divided into twelve equal parts, each semitone (half step) is an interval of the twelfth root of two so that twelve of these equal half steps add up to exactly an octave. With fretted instruments it is very useful to use an equal tempering so that the frets align evenly across the strings. In the European music tradition, equal tempering was used for lute and guitar music far earlier than for other instruments.

Equally-tempered scales have been used and instruments built using various other numbers of equal intervals. The 19 equal temperament

19 equal temperament

In music, 19 equal temperament, called 19-TET, 19-EDO, or 19-ET, is the tempered scale derived by dividing the octave into 19 equal steps . Each step represents a frequency ratio of 21/19, or 63.16 cents...

, first proposed and used by Guillaume Costeley

Guillaume Costeley

Guillaume Costeley was a French composer of the Renaissance. He was the court organist to Charles IX of France and famous for his numerous chansons, which were representative of the late development of the form; his work in this regard was part of the early development of the style known as...

in the sixteenth century, uses 19 equally spaced tones, offering better major thirds and far better minor thirds than normal 12-semitone equal temperament at the cost of a flatter fifth. The overall effect is one of greater consonance. 24 equal temperament, with 24 equally spaced tones, is widespread in Arabic music.

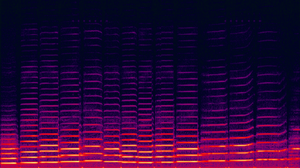
The following graph reveals how accurately various equal-tempered scales approximate three important harmonic identities: the major third (5th harmonic), the perfect fifth (3rd harmonic), and the "harmonic seventh

Harmonic seventh

The harmonic seventh interval , also known as the septimal minor seventh, or subminor seventh, is one with an exact 7:4 ratio . This is somewhat narrower than and is "sweeter in quality" than an "ordinary" minor seventh, which has a just-intonation ratio of 9:5 , or an equal-temperament ratio of...

" (7th harmonic). [Note: the numbers above the bars designate the equal-tempered scale (I.e., "12" designates the 12-tone equal-tempered scale, etc.)]

Note	Frequency (Hz)	Frequency Distance from previous note	Log frequency log₂ f	Log frequency Distance from previous note
A₂	110.00	N/A	6.781	N/A
A₂#	116.54	6.54	6.864	0.0833 (or 1/12)
B₂	123.47	6.93	6.948	0.0833
C₂	130.81	7.34	7.031	0.0833
C₂#	138.59	7.78	7.115	0.0833
D₂	146.83	8.24	7.198	0.0833
D₂#	155.56	8.73	7.281	0.0833
E₂	164.81	9.25	7.365	0.0833
F₂	174.61	9.80	7.448	0.0833
F₂#	185.00	10.39	7.531	0.0833
G₂	196.00	11.00	7.615	0.0833
G₂#	207.65	11.65	7.698	0.0833
A₃	220.00	12.35	7.781	0.0833

Below are Ogg Vorbis files demonstrating the difference between just intonation and equal temperament. You may need to play the samples several times before you can pick the difference.

Two sine waves played consecutively - this sample has half-step at 550 Hz (C# in the just intonation scale), followed by a half-step at 554.37 Hz (C# in the equal temperament scale).
Same two notes, set against an A440 pedal - this sample consists of a "dyad
Dyad (music)
In music, a dyad is a set of two notes or pitches. Although most chords have three or more notes, in certain contexts a dyad may be considered to be a chord. The most common two-note chord is made from the interval of a perfect fifth, which may be suggestive of music of the Medieval or Renaissance...

". The lower note is a constant A (440 Hz in either scale), the upper note is a C# in the equal-tempered scale for the first 1", and a C# in the just intonation scale for the last 1". Phase
Beat (acoustics)
In acoustics, a beat is an interference between two sounds of slightly different frequencies, perceived as periodic variations in volume whose rate is the difference between the two frequencies....

differences make it easier to pick the transition than in the previous sample.

Connections to set theory

Musical set theory uses some of the concepts from mathematical set theory

Set theory

to organize musical objects and describe their relationships. To analyze the structure of a piece of (typically atonal) music using musical set theory, one usually starts with a set of tones, which could form motives or chords. By applying simple operations such as transposition

Transposition (music)

In music transposition refers to the process, or operation, of moving a collection of notes up or down in pitch by a constant interval.For example, one might transpose an entire piece of music into another key...

and inversion

Inversion (music)

In music theory, the word inversion has several meanings. There are inverted chords, inverted melodies, inverted intervals, and inverted voices...

, one can discover deep structures in the music. Operations such as transposition and inversion are called isometries because they preserve the intervals between tones in a set.

Connections to abstract algebra

Expanding on the methods of musical set theory, many theorists have used abstract algebra to analyze music. For example, the notes in an equal temperament octave form an abelian group

Abelian group

In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...

with 12 elements. It is possible to describe just intonation

Just intonation

in terms of a free abelian group

Free abelian group

In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...

.

Transformational theory

Transformational theory

Transformational theory is a branch of music theory developed by David Lewin in the 1980s, and formally introduced in his most influential work, Generalized Musical Intervals and Transformations...

is a branch of music theory developed by David Lewin

David Lewin

David Lewin was an American music theorist, music critic and composer. Called "the most original and far-ranging theorist of his generation" , he did his most influential theoretical work on the development of transformational theory, which involves the application of mathematical group theory to...

. The theory allows for great generality because it emphasizes transformations between musical objects, rather than the musical objects themselves.

Theorists have also proposed musical applications of more sophisticated algebraic concepts. Mathematician Guerino Mazzola

Guerino Mazzola

Guerino Mazzola is a Swiss mathematician, musicologist, jazz pianist as well as book writer.He graduated at the University of Zürich in Mathematics, Theoretical Physics and Crystallography and completed his PhD in Mathematics in 1971. In 1980, he habilitated in Algebraic Geometry and...

has applied topos theory to music, though the result has been controversial.

The chromatic scale has a free and transitive action of

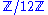, with the action being defined via transposition

Transposition (music)

of notes. So the chromatic scale can be thought of as a torsor for the group

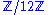Connections to number theory

Modern interpretation of just intonation

Just intonation

is fully based on fundamental theorem of arithmetic

Fundamental theorem of arithmetic

In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...

The golden ratio and Fibonacci numbers

It is believed that some composers wrote their music using the golden ratio

Golden ratio

and the Fibonacci number

Fibonacci number

In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....

s to assist them. However, regarding the listener, the degree to which the application of the golden ratio in music is salient, whether consciously or unconsciously, as well as the overall musical effect of its implementation, if any, is unknown.

James Tenney

James Tenney

James Tenney was an American composer and influential music theorist.-Biography:Tenney was born in Silver City, New Mexico, and grew up in Arizona and Colorado. He attended the University of Denver, the Juilliard School of Music, Bennington College and the University of Illinois...

reconceived his piece "For Ann (Rising)", which consists of up to twelve computer-generated tones that glissando

Glissando

In music, a glissando is a glide from one pitch to another. It is an Italianized musical term derived from the French glisser, to glide. In some contexts it is distinguished from the continuous portamento...

upwards (see Shepard tone

Shepard tone

A Shepard tone, named after Roger Shepard, is a sound consisting of a superposition of sine waves separated by octaves. When played with the base pitch of the tone moving upward or downward, it is referred to as the Shepard scale. This creates the auditory illusion of a tone that continually...

), as having each tone start so each is the golden ratio (in between an equal-tempered minor

Minor sixth

-Subminor sixth:In music, a subminor sixth or septimal sixth is an interval that is noticeably narrower than a minor sixth but noticeably wider than a diminished sixth.The sub-minor sixth is an interval of a 14:9 ratio or alternately 11:7....

and major sixth

Major sixth

In classical music from Western culture, a sixth is a musical interval encompassing six staff positions , and the major sixth is one of two commonly occurring sixths. It is qualified as major because it is the largest of the two...

) below the previous tone, so that the combination tones produced by all consecutive tones are a lower or higher pitch already, or soon to be, produced.

Ernő Lendvaï

Erno Lendvai

Ernő Lendvai was one of the first theorists to write on the appearance of the golden section and Fibonacci series and how these are implemented in Bartók's music...

analyzes Béla Bartók's

Béla Bartók

Béla Viktor János Bartók was a Hungarian composer and pianist. He is considered one of the most important composers of the 20th century and is regarded, along with Liszt, as Hungary's greatest composer...

works as being based on two opposing systems: those of the golden ratio and the acoustic scale. In Bartok's Music for Strings, Percussion, and Celesta, the xylophone

Xylophone

The xylophone is a musical instrument in the percussion family that consists of wooden bars struck by mallets...

progression at the beginning of the 3rd movement occurs at the intervals 1:2:3:5:8:5:3:2:1. French composer Erik Satie

Erik Satie

Éric Alfred Leslie Satie was a French composer and pianist. Satie was a colourful figure in the early 20th century Parisian avant-garde...

used the golden ratio in several of his pieces, including Sonneries de la Rose Croix.

The golden ratio is also apparent in the organization of the sections in the music of Debussy's

Claude Debussy

Claude-Achille Debussy was a French composer. Along with Maurice Ravel, he was one of the most prominent figures working within the field of impressionist music, though he himself intensely disliked the term when applied to his compositions...

Image, "Reflections in Water", in which the sequence of keys is marked out by the intervals 34, 21, 13, and 8 (a descending Fibonacci sequence), and the main climax sits at the φ

Golden ratio

position.

External links

Database of all the possible 2048 musical scales in 12 note equal temperament and other alternatives in meantone tunings
Music and Math by Thomas E. Fiore
Twelve-Tone Musical Scale.
Sonantometry or music as math discipline.
Music: A Mathematical Offering by Dave Benson.
Nicolaus Mercator use of Ratio Theory in Music at Convergence
Finding the natural and pentatonic scales through discrete numbers
The Glass Bead Game Hermann Hesse gave music and mathematics a crucial role in the development of his Glass Bead Game.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Time, rhythm and meter

Musical form

Frequency and harmony

Tuning systems

Connections to set theory

Connections to abstract algebra

Connections to number theory

The golden ratio and Fibonacci numbers

See also

External links