
List of commutative algebra topics
Encyclopedia
Commutative algebra
is the branch of abstract algebra
that studies commutative ring
s, their ideals
, and modules
over such rings. Both algebraic geometry
and algebraic number theory
build on commutative algebra. Prominent examples of commutative rings include polynomial ring
s, rings of algebraic integer
s, including the ordinary integer
s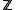 , and p-adic integer
, and p-adic integer
s.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
is the branch of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
that studies commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s, their ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
, and modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over such rings. Both algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
build on commutative algebra. Prominent examples of commutative rings include polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
s, rings of algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
s, including the ordinary integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s
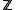 , and p-adic integer
, and p-adic integerP-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s.
Basic notions
- Commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
- Module (mathematics)Module (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
- Ring ideal, maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
, prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers... - Ring homomorphismRing homomorphismIn ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
- Ring monomorphism
- Ring epimorphism
- Ring isomorphism
- Zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
- Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
Classes of rings
- Field (mathematics)Field (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
- Algebraic number fieldAlgebraic number fieldIn mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
- Polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
- Integral domain
- Boolean algebra (structure)
- Principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
- Euclidean domainEuclidean domainIn mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
- Unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
- Dedekind domainDedekind domainIn abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
- NilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
elements and reduced ringReduced ringIn ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
s - Dual numbers
- Tensor product of fieldsTensor product of fieldsIn abstract algebra, the theory of fields lacks a direct product: the direct product of two fields, considered as a ring is never itself a field. On the other hand it is often required to 'join' two fields K and L, either in cases where K and L are given as subfields of a larger field M, or when K...
- Tensor product of R-algebras
Constructions with commutative rings
- Quotient ringQuotient ringIn ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
- Field of fractionsField of fractionsIn abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
- Product of ringsProduct of ringsIn mathematics, it is possible to combine several rings into one large product ring. This is done as follows: if I is some index set and Ri is a ring for every i in I, then the cartesian product Πi in I Ri can be turned into a ring by defining the operations coordinatewise, i.e...
- Annihilator (ring theory)Annihilator (ring theory)In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
- Integral closure
Localization and completion
- Completion (ring theory)Completion (ring theory)In abstract algebra, a completion is any of several related functors on rings and modules that result in complete topological rings and modules. Completion is similar to localization, and together they are among the most basic tools in analysing commutative rings. Complete commutative rings have...
- Formal power seriesFormal power seriesIn mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
- Localization of a ringLocalization of a ringIn abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
- Local ringLocal ringIn abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
- Local ring
- Regular local ringRegular local ringIn commutative algebra, a regular local ring is a Noetherian local ring having the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of...
- Localization of a module
- Valuation (mathematics)
- Discrete valuation
- Discrete valuation ringDiscrete valuation ringIn abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
- I-adic topology
- Weierstrass preparation theoremWeierstrass preparation theoremIn mathematics, the Weierstrass preparation theorem is a tool for dealing with analytic functions of several complex variables, at a given point P...
Finiteness properties
- Noetherian ringNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
- Hilbert's basis theoremHilbert's basis theoremIn mathematics, specifically commutative algebra, Hilbert's basis theorem states that every ideal in the ring of multivariate polynomials over a Noetherian ring is finitely generated. This can be translated into algebraic geometry as follows: every algebraic set over a field can be described as the...
- Artinian ringArtinian ringIn abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
- Ascending chain conditionAscending chain conditionThe ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
(ACC) and descending chain condition (DCC)
Ideal theory
- Fractional idealFractional idealIn mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
- Ideal class groupIdeal class groupIn mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
- Radical of an idealRadical of an idealIn commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
- Hilbert's NullstellensatzHilbert's NullstellensatzHilbert's Nullstellensatz is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields...
Homological properties
- Flat moduleFlat moduleIn Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
- Flat mapFlat mapThe flat map in differential geometry is a name for the mapping that converts coordinate basis vectors into corresponding coordinate 1-forms.A flat map in ring theory is a homomorphism f from a ring R to a ring S such that S is a flat R-module, where the action of R on S is given by f....
- Projective moduleProjective moduleIn mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
- Injective moduleInjective moduleIn mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
- Cohen-Macaulay ringCohen-Macaulay ringIn mathematics, a Cohen–Macaulay ring is a particular type of commutative ring, possessing some of the algebraic-geometric properties of a nonsingular variety, such as local equidimensionality....
- Gorenstein ringGorenstein ringIn commutative algebra, a Gorenstein local ring is a Noetherian commutative local ring R with finite injective dimension, as an R-module. There are many equivalent conditions, some of them listed below, most dealing with some sort of duality condition....
- Complete intersection ring
- Koszul complexKoszul complexIn mathematics, the Koszul complex was first introduced to define a cohomology theory for Lie algebras, by Jean-Louis Koszul...
- Hilbert's syzygy theoremHilbert's syzygy theoremIn mathematics, Hilbert's syzygy theorem is a result of commutative algebra, first proved by David Hilbert in connection with the syzygy problem of invariant theory. Roughly speaking, starting with relations between polynomial invariants, then relations between the relations, and so on, it...
- Quillen–Suslin theoremQuillen–Suslin theoremThe Quillen–Suslin theorem, also known as Serre's problem or Serre's conjecture, is a theorem in commutative algebra about the relationship between free modules and projective modules over polynomial rings...
Dimension theory
- Height (ring theory)
- Depth (ring theory)Depth (ring theory)In commutative and homological algebra, depth is an important invariant of rings and modules. Although depth can be defined more generally, the most common case considered is the case of modules over a commutative Noetherian local ring. In this case, the depth of a module is related with its...
- Hilbert polynomialHilbert polynomialIn commutative algebra, the Hilbert polynomial of a graded commutative algebra or graded module is a polynomial in one variable that measures the rate of growth of the dimensions of its homogeneous components...
- Regular local ringRegular local ringIn commutative algebra, a regular local ring is a Noetherian local ring having the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of...
- Discrete valuation ringDiscrete valuation ringIn abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
- Discrete valuation ring
- Global dimensionGlobal dimensionIn ring theory and homological algebra, the global dimension of a ring A denoted gl dim A, is a non-negative integer or infinity which is a homological invariant of the ring. It is defined to be the supremum of the set of projective dimensions of all A-modules...
- Regular sequence (algebra)Regular sequence (algebra)In commutative algebra, if R is a commutative ring and M an R-module, a nonzero element r in R is called M-regular if r is not a zerodivisor on M, and M/rM is nonzero...
- Krull dimensionKrull dimensionIn commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
- Krull's principal ideal theoremKrull's principal ideal theoremIn commutative algebra, Krull's principal ideal theorem, named after Wolfgang Krull , gives a bound on the height of a principal ideal in a Noetherian ring...
Ring extensions, primary decomposition
- Primary idealPrimary idealIn mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
- Primary decomposition and the Lasker–Noether theoremLasker–Noether theoremIn mathematics, the Lasker–Noether theorem states that every Noetherian ring is a Lasker ring, which means that every ideal can be written as an intersection of finitely many primary ideals...
- Noether normalization lemmaNoether normalization lemmaIn mathematics, the Noether normalization lemma is a result of commutative algebra, introduced in . A simple version states that for any field k, and any finitely generated commutative k-algebra A, there exists a nonnegative integer d and algebraically independent elements y1, y2, ..., yd in Asuch...
- Going up and going downGoing up and going downIn commutative algebra, a branch of mathematics, going up and going down are terms which refer to certain properties of chains of prime ideals in integral extensions....
Relation with algebraic geometry
- Spectrum of a ringSpectrum of a ringIn abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
- Zariski tangent spaceZariski tangent spaceIn algebraic geometry, the Zariski tangent space is a construction that defines a tangent space at a point P on an algebraic variety V...
- Kähler differentialKähler differentialIn mathematics, Kähler differentials provide an adaptation of differential forms to arbitrary commutative rings or schemes.-Presentation:The idea was introduced by Erich Kähler in the 1930s...
Computational and algorithmic aspects
- Elimination theoryElimination theoryIn commutative algebra and algebraic geometry, elimination theory is the classical name for algorithmic approaches to eliminating between polynomials of several variables....
- Gröbner basisGröbner basisIn computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
- Buchberger's algorithmBuchberger's algorithmIn computational algebraic geometry and computational commutative algebra, Buchberger's algorithm is a method of transforming a given set of generators for a polynomial ideal into a Gröbner basis with respect to some monomial order. It was invented by Austrian mathematician Bruno Buchberger...
Related disciplines
- Algebraic number theoryAlgebraic number theoryAlgebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
- Algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
- Ring theoryRing theoryIn abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
- Field theory (mathematics)Field theory (mathematics)Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
- Differential algebraDifferential algebraIn mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
- Homological algebraHomological algebraHomological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...

