List of first-order theories
Encyclopedia
In mathematical logic
, a first-order theory
is given by a set of axioms in some
language. This entry lists some of the more common examples used in model theory
and some of their properties.
σ listing the constants, functions, and relations of the theory together with their valences, so that the object is naturally a σ-structure
. Given a signature σ there is a unique first-order language Lσ that can be used to capture the first-order expressible facts about the σ-structure.
There are two common ways to specify theories:
An Lσ theory may:
Pure identity theory has no (non-logical) axioms. It is decidable.
One of the few interesting properties that can be stated in the language of pure identity theory is that of being infinite.
This is given by an infinite set of axioms stating there are at least 2 elements, there are at least 3 elements, and so on:
These axioms define the theory of an infinite set.
The opposite property of being finite cannot be stated in first-order logic for any theory that has arbitrarily large finite models: in fact any such theory has infinite models by the compactness theorem
. In general if a property can be stated by a finite number of sentences of first-order logic then the opposite property can also be stated in first-order logic, but if a property needs an infinite number of sentences then its opposite property cannot be stated in first-order logic.
Any statement of pure identity theory is equivalent to either σ(N) or to ¬σ(N) for some finite subset N of the non-negative integers, where σ(N) is the statement that the number of elements is in N. It is even possible to describe all possible theories in this language as follows. Any theory is either the theory of all sets of cardinality in N for some finite subset N of the non-negative integers, or the theory of all sets whose cardinality is not in N, for some finite or infinite subset N of the non-negative integers. (There are no theories whose models are exactly sets of cardinality N if N is an infinite subset of the integers.) The complete theories are the theories of sets of cardinality n for some finite n, and the theory of infinite sets.
One special case of this is the inconsistent theory defined by the axiom ∃x ¬x = x. It is a perfectly good theory with many good properties: it is complete, decidable, finitely axiomatizable, and so on. The only problem is that it has no models at all. By Gödel's completeness theorem, it is the only theory (for any given language) with no models.
The theory of a countable number of independent unary relations is complete, but has no atomic models. It is also an example of a theory that is superstable but not totally transcendental.
Equivalence relation
The signature of equivalence relation
s has one binary infix relation symbol ~, no constants, and no functions. Equivalence relations satisfy the axioms:
Some first order properties of equivalence relations are:
The theory of an equivalence relation with exactly 2 infinite equivalence classes is an easy example of a theory which is ω-categorical but not categorical for any larger cardinal
.
The equivalence relation ~ should not be confused with the identity
symbol '=': if x=y then x~y, but the converse is not necessarily true. Theories of equivalence relations are not all that difficult or interesting, but often give easy examples or counterexamples for various statements.
The following constructions are sometimes used to produce examples of theories with certain spectra
; in fact by applying them to a small number of explicit theories T one gets examples of complete countable theories with all possible uncountable spectra. If T is a theory in some language, we define a new theory 2T by adding a new binary relation to the language, and adding axioms stating that it is an equivalence relation, such that there are an infinite number of equivalence classes all of which are model
s of T. It is possible to iterate this construction transfinitely: given an ordinal
α, define a new theory by adding an equivalence relation Eβ for each β<α, together with axioms stating that whenever β<γ then each Eγ equivalence class is the union of infinitely many Eβ equivalence classes, and each E0 equivalence class is a model of T. Informally, one can visualize models of this theory as infinitely branching trees of height α with models of T attached to all leaves.
We define x≥y, x<y, x>y as abbreviations for y≤x, x≤y ∧¬y≤x, y<x,
Some first-order properties of orders:
The theory DLO of dense linear orders with no endpoints (i.e. no smallest or largest element) is complete, ω-categorical, but not categorical for any uncountable cardinal. There are 3 other very similar theories: the theory of dense linear orders with a:
Being well ordered ("any non-empty subset has a minimal element") is not a first-order property; the usual definition involves quantifying over all subsets.
can be considered either as special sorts of partially ordered sets, with a signature consisting of one binary relation symbol ≤, or as algebraic structures with a signature consisting of two binary operations ∧ and ∨. The two approaches can be related by defining a≤ b to mean a∧b=a.
For two binary operations the axioms for a lattice are:
For one relation ≤ the axioms are:
First order properties include:
Completeness
is not a first order property of lattice.
The axioms for the theory of graphs areAnti-reflexive: ∀ x ¬R(x,x) ("no loops")
The theory of random graphs has the following extra axioms for each positive integer n:
The theory of random graphs is ω categorical, complete, and decidable, and its countable model is called the Rado graph
. A statement in the language of graphs is true in this theory if and only if it is true with probability 1 for a random graph
on a countable number of points.
The axioms are:
Tarski proved that the theory of Boolean algebras is decidable.
We write x ≤ y as an abbreviation for x ∧ y = x, and atom(x) as an abbreviation for ¬x = 0 ∧ ∀y y≤x → y = 0 ∨ y = x, read as "x is an atom", in other words a non-zero element with nothing between it and 0. Here are some first-order properties of Boolean algebras:Atomless: ∀ x ¬atom(x)
The theory of atomless Boolean algebras is ω-categorical and complete.
For any Boolean algebra B, there are several invariants defined as follows.The quotient algebras Bi of B are defined inductively by B0=B, Bk+1 = Bk/I(Bk).
The invariant m(B) is the smallest integer such that Bm+1 is trivial, or ∞ if no such integer exists.
If m(B) is finite, the invariant n(B) is the number of atoms of Bm(B) if this number is finite, or ∞ if this number is infinite.
The invariant l(B) is 0 if Bm(B) is atomic or if m(B) is ∞, and 1 otherwise.
Then two Boolean algebras are elementarily equivalent if and only if their invariants l, m, and n are the same. In other words, the values of these invariants classify the possible completions of the theory of Boolean algebras. So the possible complete theories are:The theories with m a natural number, n a natural number or ∞, and l = 0 or 1 (with l = 0 if n=0).
(the inverse) whose value on t is denoted by t−1, and one function
of arity 2, which is usually omitted from terms. For any integer n. tn is an abbreviation for the obvious term for the nth power of t.
Group
s are defined by the axioms
Some properties of groups that can be defined in the first-order language of groups are:Torsion free ∀ x x2 = 1→x = 1, ∀x x3 = 1 → x = 1, ∀x x4 = 1 → x = 1, ...
Divisible ∀ x ∃y y2 = x, ∀x ∃y y3 = x, ∀x ∃y y4 = x, ...
Infinite (as in identity theory)
Exponent n (for any fixed positive integer n) ∀x xn = 1
Nilpotent
of class n (for any fixed positive integer n)
Solvable
of class n (for any fixed positive integer n)
The theory of Abelian groups is decidable. The theory of Infinite divisible torsion-free abelian groups is complete, as is the theory of Infinite abelian groups of exponent p (for p prime).
The theory of finite groups is the set of first-order statements in the language of groups that are true in all finite groups (there are plenty of infinite models of this theory). It is not completely trivial to find any such statement that is not true for all groups: one example is
"given two elements of order 2, either they are conjugate or there is a non-trivial element commuting with both of them".
The properties of being finite, or free, or simple, or torsion are not first-order. More precisely, the first-order theory of all groups with one of these properties has models that do not have this property.
Ring
s
Axioms: Addition makes the ring into an abelian group, multiplication is associative and has an identity 1, and multiplication is left and right distributive.
Commutative ring
s The axioms for rings plus ∀x ∀y xy=yx.
Field
s The axioms for commutative rings plus ∀x ∃y xy=1 and ¬ 1=0. Many of the examples given here have only universal, or algebraic axioms. The class of structures satisfying such a theory has the property of being closed under substructure. For example, a subset of a group closed under the group actions of multiplication and inverse is again a group. Since the signature of fields does not usually include multiplicative and additive inverse, the axioms for inverses are not universal, and therefore a substructure of a field closed under addition and multiplication is not always a field. This can be remedied by adding unary inverse functions to the language.
For any positive integer n the property that all equations of degree n have a root can be expressed by a single first-order sentence:
Perfect field
s
The axioms for fields, plus axioms for each prime number p stating that if p 1 = 0 (i.e. the field has characteristic p), then every field element has a pth root.
Algebraically closed fields of characteristic p
The axioms for fields, plus for every positive n the axiom that all polynomials of degree n have a root, plus axioms fixing the characteristic. The classical examples of complete theories. Categorical
in all uncountable cardinals. The theory ACFp has a universal domain property, in the sense that every structure N satisfying the universal axioms of ACFp is a substructure of a sufficiently large algebraically closed field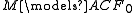
, and additionally any two such embeddings N → M induce an automorphism
of M.
Finite field
s. The theory of finite fields is the set of all first-order statements that are true in all finite fields. Significant examples of such statements can, for example, be given by applying the Chevalley–Warning theorem, over the prime fields. The name is a little misleading as the theory has plenty of infinite models. Ax proved that the theory is decidable.
Formally real field
s These are fields with the axiom
Real closed field
s
Axioms:
The theory of real closed fields is decidable (Tarski) and therefore complete.
p-adic fields: showed that the theory of p-adic fields is decidable and gave a set of axioms for it.
Some examples of axiomatized systems of geometry include ordered geometry
, absolute geometry
, affine geometry
, Euclidean geometry
, projective geometry
, and hyperbolic geometry
. For each of these geometries there are many different and inequivalent systems of axioms for various dimensions. Some of these axiom systems include "completeness" axioms that are not first order.
As a typical example, the axioms for projective geometry use 2 types, points and lines, and a binary incidence relation between points and lines. If point and line variables are indicated by small and capital letter, and a incident to A is written as aA, then one set of axioms is
Euclid did not state all the axioms for Euclidean geometry explicitly, and the first complete list was given by Hilbert in Hilbert's axioms
. This is not a first order axiomatization as one of Hilbert's axioms is a second order completeness axiom. Tarski's axioms
are a first order axiomatization of Euclidean geometry. Tarski showed this axiom system is complete and decidable by relating it to the complete and decidable theory of real closed fields.
The signature is that of fields (0, 1, +, -, ×) together with a unary function ∂, the derivation.
The axioms are those for fields together with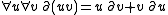
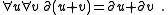
For this theory one can add the condition that the characteristic is p, a prime or zero,
to get the theory DFp of differential fields of characteristic p (and similarly with the other theories below).
If K is a differential field then the field of constants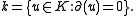
The theory of differentially perfect fields is the theory of differential fields together with the condition that the field of constants is perfect; in other words for each prime p it has the axiom: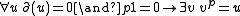
(There is little point in demanding that the whole field should be perfect field
, because in non-zero characteristic this implies the differential is 0.)
For technical reasons to do with quantifier elimination
it is sometimes more convenient to force the constant field to be perfect by adding a new symbol r to the signature with the axioms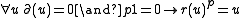
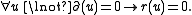
The last axiom (induction) can be replaced by the axioms
The theory of the natural numbers with a successor function is complete and decidable, and is κ-categorical for uncountable κ but not for countable κ.
Presburger arithmetic
is the theory of the natural numbers under addition, with signature consisting of a constant 0, a unary function, S, and a binary function +. It is complete and decidable. The axioms are
The signature of a theory of arithmetic has:
Some authors take the signature to contain a constant 1 instead of the function S, then define S in the obvious way as St = 1 + t.
Robinson arithmetic
(also called Q). Axioms (1) and (2) govern the distinguished element 0. (3) assures that S is an injection
. Axioms (4) and (5) are the standard recursive definition of addition; (6) and (7) do the same for multiplication. Robinson arithmetic can be thought of as Peano arithmetic without induction. Q is a weak theory for which Gödel's incompleteness theorem
holds.
Axioms:
IΣn is first order Peano arithmetic with induction restricted to Σn formulas
(for n = 0, 1, 2, ...). The theory IΣ0 is often denoted by IΔ0. This is a series of more and more powerful fragments of Peano arithmetic. The case n = 1 has about the same strength as primitive recursive arithmetic
(PRA).
Exponential function arithmetic (EFA) is IΣ0 with an axiom stating that xy exists for all x and y (with the usual properties).
First order Peano arithmetic, PA. The "standard" theory of arithmetic. The axioms are the axioms of Robinson arithmetic
above, together with the axiom scheme of induction:
Kurt Gödel
's 1931 paper proved that PA is incomplete, and has no consistent recursively enumerable completions.
Complete arithmetic (also known as true arithmetic) is the theory of the standard model of arithmetic, the natural numbers N. It is complete but does not have a recursively enumerable set of axioms.
can refer to a first order theory (in spite of the name) with two types of variables, thought of as varying over integers and subsets of the integers. (There is also a theory of arithmetic in second order logic that is called second order arithmetic. It has only one model, unlike the corresponding theory in first order logic, which is incomplete.) The signature will typically be the signature 0, S, +, × of arithmetic, together with a membership relation ∈ between integers and subsets (though there are numerous minor variations). The axioms are those of Robinson arithmetic
, together with axiom schemes of induction
and comprehension
.
There are many different subtheories of second order arithmetic that differ in which formulas are allowed in the induction and comprehension schemes.
In order of increasing strength, five of the most common systems
are
These are defined in detail in the articles on second order arithmetic and reverse mathematics
.
Some first order set theories include:
Some extra first order axioms that can be added to one of these (usually ZF) include:
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a first-order theory
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
is given by a set of axioms in some
language. This entry lists some of the more common examples used in model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
and some of their properties.
Preliminaries
For every natural mathematical structure there is a signatureSignature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
σ listing the constants, functions, and relations of the theory together with their valences, so that the object is naturally a σ-structure
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
. Given a signature σ there is a unique first-order language Lσ that can be used to capture the first-order expressible facts about the σ-structure.
There are two common ways to specify theories:
- List or describe a set of sentences in the language Lσ, called the axioms of the theory.
- Give a set of σ-structures, and define a theory to be the set of sentences in Lσ holding in all these models. For example, the "theory of finite fields" consists of all sentences in the language of fields that are true in all finite fields.
An Lσ theory may:
- be consistent: no proof of contradiction exists;
- be satisfiable: there exists a σ-structure for which the sentences of the theory are all true (by the completeness theorem, satisfiability is equivalent to consistency);
- be complete: for any statement, either it or its negation is provable;
- have quantifier eliminationQuantifier eliminationQuantifier elimination is a concept of simplification used in mathematical logic, model theory, and theoretical computer science. One way of classifying formulas is by the amount of quantification...
; - eliminate imaginaries;
- be finitely axiomatizable;
- be decidableDecidability (logic)In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
: There is an algorithm to decide which statements are provable; - be recursively axiomatizable;
- be Model complete or sub-model complete;
- be κ-categoricalMorley's categoricity theoremIn model theory, a branch of mathematical logic, a theory is κ-categorical if it has exactly one model of cardinality κ up to isomorphism....
: All models of cardinality κ are isomorphic; - be StableStable theoryIn model theory, a complete theory is called stable if it does not have too many types. One goal of classification theory is to divide all complete theories into those whose models can be classified and those whose models are too complicated to classify, and to classify all models in the cases...
or unstable. - be ω-stable (same as totally transcendental for countable theories).
- be superstable
- have an atomic model
- have a prime modelPrime modelIn mathematics, and in particular model theory, a prime model is a model which is as simple as possible. Specifically, a model P is prime if it admits an elementary embedding into any model M to which it is elementarily equivalent .- Cardinality :In contrast with the notion of saturated model,...
- have a saturated modelSaturated modelIn mathematical logic, and particularly in its subfield model theory, a saturated model M is one which realizes as many complete types as may be "reasonably expected" given its size...
Pure identity theories
The signature of the pure identity theory is empty, with no functions, constants, or relations.Pure identity theory has no (non-logical) axioms. It is decidable.
One of the few interesting properties that can be stated in the language of pure identity theory is that of being infinite.
This is given by an infinite set of axioms stating there are at least 2 elements, there are at least 3 elements, and so on:
- ∃x1 ∃x2 ¬x1 = x2, ∃x1 ∃x2 ∃x3 ¬x1 = x2 ∧ ¬x1 = x3 ∧ ¬x2 = x3,...
These axioms define the theory of an infinite set.
The opposite property of being finite cannot be stated in first-order logic for any theory that has arbitrarily large finite models: in fact any such theory has infinite models by the compactness theorem
Compactness theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
. In general if a property can be stated by a finite number of sentences of first-order logic then the opposite property can also be stated in first-order logic, but if a property needs an infinite number of sentences then its opposite property cannot be stated in first-order logic.
Any statement of pure identity theory is equivalent to either σ(N) or to ¬σ(N) for some finite subset N of the non-negative integers, where σ(N) is the statement that the number of elements is in N. It is even possible to describe all possible theories in this language as follows. Any theory is either the theory of all sets of cardinality in N for some finite subset N of the non-negative integers, or the theory of all sets whose cardinality is not in N, for some finite or infinite subset N of the non-negative integers. (There are no theories whose models are exactly sets of cardinality N if N is an infinite subset of the integers.) The complete theories are the theories of sets of cardinality n for some finite n, and the theory of infinite sets.
One special case of this is the inconsistent theory defined by the axiom ∃x ¬x = x. It is a perfectly good theory with many good properties: it is complete, decidable, finitely axiomatizable, and so on. The only problem is that it has no models at all. By Gödel's completeness theorem, it is the only theory (for any given language) with no models.
Unary relations
A set of unary relations Pi for i in some set I is called independent if for every two disjoint finite subsets A and B of I there is some element x such that Pi(x) is true for i in A and false for i in B. Independence can be expressed by a set of first-order statements.The theory of a countable number of independent unary relations is complete, but has no atomic models. It is also an example of a theory that is superstable but not totally transcendental.
Equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s
The signature of equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s has one binary infix relation symbol ~, no constants, and no functions. Equivalence relations satisfy the axioms:
- ReflexivityReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
∀x x~x; - SymmetrySymmetric relationIn mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
∀x ∀y x~y → y~x; - TransitivityTransitive relationIn mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
: ∀x ∀y ∀z (x~y ∧ y~z) → x~z.
Some first order properties of equivalence relations are:
- ~ has an infinite number of equivalence classes;
- ~ has exactly n equivalence classes (for any fixed positive integer n);
- All equivalence classes are infinite;
- All equivalence classes have size exactly n (for any fixed positive integer n).
The theory of an equivalence relation with exactly 2 infinite equivalence classes is an easy example of a theory which is ω-categorical but not categorical for any larger cardinal
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
.
The equivalence relation ~ should not be confused with the identity
Identity (philosophy)
In philosophy, identity, from , is the relation each thing bears just to itself. According to Leibniz's law two things sharing every attribute are not only similar, but are the same thing. The concept of sameness has given rise to the general concept of identity, as in personal identity and...
symbol '=': if x=y then x~y, but the converse is not necessarily true. Theories of equivalence relations are not all that difficult or interesting, but often give easy examples or counterexamples for various statements.
The following constructions are sometimes used to produce examples of theories with certain spectra
Spectrum of a theory
In model theory, a branch of mathematical logic, the spectrum of a theoryis given by the number of isomorphism classes of models in various cardinalities. More precisely,...
; in fact by applying them to a small number of explicit theories T one gets examples of complete countable theories with all possible uncountable spectra. If T is a theory in some language, we define a new theory 2T by adding a new binary relation to the language, and adding axioms stating that it is an equivalence relation, such that there are an infinite number of equivalence classes all of which are model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
s of T. It is possible to iterate this construction transfinitely: given an ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
α, define a new theory by adding an equivalence relation Eβ for each β<α, together with axioms stating that whenever β<γ then each Eγ equivalence class is the union of infinitely many Eβ equivalence classes, and each E0 equivalence class is a model of T. Informally, one can visualize models of this theory as infinitely branching trees of height α with models of T attached to all leaves.
Orders
The signature of orders has no constants or functions, and one binary relation symbols ≤. (It is of course possible to use ≥, < or > instead as the basic relation, with the obvious minor changes to the axioms.)We define x≥y, x<y, x>y as abbreviations for y≤x, x≤y ∧¬y≤x, y<x,
Some first-order properties of orders:
- Transitive: ∀x ∀y ∀z x ≤ y∧y ≤ z → x ≤ z
- Reflexive: ∀x x ≤ x
- Antisymmetric: ∀x ∀y x ≤ y ∧ y ≤ x → x = y
- Partial: Transitive∧Reflexive∧Antisymmetric;
- Linear (or total): Partial ∧ ∀x ∀y x≤y ∨ y≤x
- Dense ∀x ∀z x<z → ∃y x<y ∧ y<z ("Between any 2 distinct elements there is another element")
- There is a smallest element: ∃x ∀y x≤y
- There is a largest element: ∃x ∀y y≤x
- Every element has an immediate successor: ∀x ∃y ∀z x<z ↔ y≤z
The theory DLO of dense linear orders with no endpoints (i.e. no smallest or largest element) is complete, ω-categorical, but not categorical for any uncountable cardinal. There are 3 other very similar theories: the theory of dense linear orders with a:
- Smallest but no largest element;
- Largest but no smallest element;
- Largest and smallest element.
Being well ordered ("any non-empty subset has a minimal element") is not a first-order property; the usual definition involves quantifying over all subsets.
Lattices
LatticesLattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
can be considered either as special sorts of partially ordered sets, with a signature consisting of one binary relation symbol ≤, or as algebraic structures with a signature consisting of two binary operations ∧ and ∨. The two approaches can be related by defining a≤ b to mean a∧b=a.
For two binary operations the axioms for a lattice are:
| Commutative laws: |  |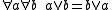
 |
||
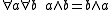| Associative Associativity In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not... laws: |
 |
 |
||
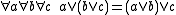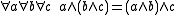| Absorption law Absorption law In algebra, the absorption law or absorption identity is an identity linking a pair of binary operations.Two binary operations, say ¤ and *, are said to be connected by the absorption law if:... s: |
 |
 |
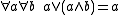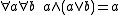For one relation ≤ the axioms are:
- Axioms stating ≤ is a partial order, as above.
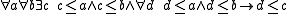(existence of c=a∧b)
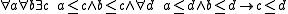(existence of c=a∨b)
First order properties include:
-
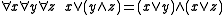(distributive latticeDistributive latticeIn mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
s) -
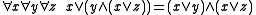(modular latticeModular latticeIn the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular law: x ≤ b implies x ∨ = ∧ b,where ≤ is the partial order, and ∨ and ∧ are...
s)
Completeness
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
is not a first order property of lattice.
Graphs
The signature of graphs has no constants or functions, and one binary relation symbol R, where R(x,y) is read as "there is an edge from x to y".The axioms for the theory of graphs are
- Symmetric: ∀
The theory of random graphs has the following extra axioms for each positive integer n:
- For any two disjoint finite sets of size
The theory of random graphs is ω categorical, complete, and decidable, and its countable model is called the Rado graph
Rado graph
In the mathematical field of graph theory, the Rado graph, also known as the random graph or the Erdős–Renyi graph, is the unique countable graph R such that for any finite graph G and any vertex v of G, any embedding of G − v as an induced subgraph of R can be extended to an...
. A statement in the language of graphs is true in this theory if and only if it is true with probability 1 for a random graph
Random graph
In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
on a countable number of points.
Boolean algebras
There are several different signatures and conventions used for Boolean algebras:- The signature has 2 constants, 0 and 1, and two binary functions ∧ and ∨ ("and" and "or"), and one unary function ¬ ("not"). This is a little confusing as the functions use the same symbols as the propositional functionPropositional functionA propositional function in logic, is a statement expressed in a way that would assume the value of true or false, except that within the statement is a variable that is not defined or specified, which leaves the statement undetermined...
s of first-order logic. - In set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a common convention is that the language has 2 constants, 0 and 1, and two binary functions · and +, and one unary function −. The three functions have the same interpretation as the functions in the first convention. Unfortunately, this convention clashes badly with the next convention: - In algebra, the usual convention is that the language has 2 constants, 0 and 1, and two binary functions · and +. The function · has the same meaning as ∧, but a+b means a∨b∧¬(a∧b). The reason for this is that the axioms for a Boolean algebra are then just the axioms for a ring with 1 plus ∀x x2 = x. Unfortunately this clashes with the standard convention in set theory given above.
The axioms are:
- The axioms for a distributive lattice (see above)
- ∀a∀b a∧¬a = 0, ∀a∀b a∨¬a = 1 (properties of negation)
- Some authors add the extra axiom ¬0=1, to exclude the trivial algebra with one element.
Tarski proved that the theory of Boolean algebras is decidable.
We write x ≤ y as an abbreviation for x ∧ y = x, and atom(x) as an abbreviation for ¬x = 0 ∧ ∀y y≤x → y = 0 ∨ y = x, read as "x is an atom", in other words a non-zero element with nothing between it and 0. Here are some first-order properties of Boolean algebras:
- Atomic: ∀
The theory of atomless Boolean algebras is ω-categorical and complete.
For any Boolean algebra B, there are several invariants defined as follows.
- the ideal
Then two Boolean algebras are elementarily equivalent if and only if their invariants l, m, and n are the same. In other words, the values of these invariants classify the possible completions of the theory of Boolean algebras. So the possible complete theories are:
- The trivial algebra (if this is allowed; sometimes 0≠1 is included as an axiom.)
- The theory with
Groups
The signature of group theory has one constant 1 (the identity), one function of arity 1(the inverse) whose value on t is denoted by t−1, and one function
of arity 2, which is usually omitted from terms. For any integer n. tn is an abbreviation for the obvious term for the nth power of t.
Group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s are defined by the axioms
Some properties of groups that can be defined in the first-order language of groups are:
- Abelian ∀
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
of class
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
of class
The theory of Abelian groups is decidable. The theory of Infinite divisible torsion-free abelian groups is complete, as is the theory of Infinite abelian groups of exponent p (for p prime).
The theory of finite groups is the set of first-order statements in the language of groups that are true in all finite groups (there are plenty of infinite models of this theory). It is not completely trivial to find any such statement that is not true for all groups: one example is
"given two elements of order 2, either they are conjugate or there is a non-trivial element commuting with both of them".
The properties of being finite, or free, or simple, or torsion are not first-order. More precisely, the first-order theory of all groups with one of these properties has models that do not have this property.
Rings and fields
The signature of (unital) rings has 2 constants 0 and 1, two binary functions + and ×, and, optionally, one unary inverse functions − −1.Ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s
Axioms: Addition makes the ring into an abelian group, multiplication is associative and has an identity 1, and multiplication is left and right distributive.
Commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s The axioms for rings plus ∀x ∀y xy=yx.
Field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s The axioms for commutative rings plus ∀x ∃y xy=1 and ¬ 1=0. Many of the examples given here have only universal, or algebraic axioms. The class of structures satisfying such a theory has the property of being closed under substructure. For example, a subset of a group closed under the group actions of multiplication and inverse is again a group. Since the signature of fields does not usually include multiplicative and additive inverse, the axioms for inverses are not universal, and therefore a substructure of a field closed under addition and multiplication is not always a field. This can be remedied by adding unary inverse functions to the language.
For any positive integer n the property that all equations of degree n have a root can be expressed by a single first-order sentence:
- ∀
Perfect field
Perfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
s
The axioms for fields, plus axioms for each prime number p stating that if p 1 = 0 (i.e. the field has characteristic p), then every field element has a pth root.
Algebraically closed fields of characteristic p
The axioms for fields, plus for every positive n the axiom that all polynomials of degree n have a root, plus axioms fixing the characteristic. The classical examples of complete theories. Categorical
Categorical
See:* Categorical imperative* Morley's categoricity theorem* Categorical data analysis* Categorical distribution* Categorical logic* Categorical syllogism* Categorical proposition* Categorization* Categorical perception* Category theory...
in all uncountable cardinals. The theory ACFp has a universal domain property, in the sense that every structure N satisfying the universal axioms of ACFp is a substructure of a sufficiently large algebraically closed field
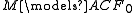, and additionally any two such embeddings N → M induce an automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of M.
Finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s. The theory of finite fields is the set of all first-order statements that are true in all finite fields. Significant examples of such statements can, for example, be given by applying the Chevalley–Warning theorem, over the prime fields. The name is a little misleading as the theory has plenty of infinite models. Ax proved that the theory is decidable.
Formally real field
Formally real field
In mathematics, in particular in field theory and real algebra, a formally real field is a field that admits an ordering which makes it an ordered field.-Alternative Definitions:...
s These are fields with the axiom
- For every positive n, the axiom ∀ a1 ∀ a2... ∀ an a1a1+a2a2+ ...+anan=0 → a1=0∨a2=0∨ ... ∨an=0 (0 is not a non-trivial sum of squares).
Real closed field
Real closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
s
Axioms:
- ∀x ∃y x=yy ∨ x+yy=0.
- For every odd positive n, the axiom stating that every polynomial of degree n has a root.
- For every positive n, the axiom ∀ a1 ∀ a2... ∀ an a1a1+a2a2+ ...+anan=0 → a1=0∨a2=0∨ ... ∨an=0 (0 is not a non-trivial sum of squares).
The theory of real closed fields is decidable (Tarski) and therefore complete.
p-adic fields: showed that the theory of p-adic fields is decidable and gave a set of axioms for it.
Geometry
Axioms for various systems of geometry usually use a typed language, with the different types corresponding to different geometric objects such as points, lines, circles, planes, and so on. The signature will often consist of binary incidence relations between objects of different types; for example, the relation that a point lies on a line. The signature may have more complicated relations; for example ordered geometry might have a ternary "betweenness" relation for 3 points, which says whether one lies between two others, or a "congruence" relation between 2 pairs of points.Some examples of axiomatized systems of geometry include ordered geometry
Ordered geometry
Ordered geometry is a form of geometry featuring the concept of intermediacy but, like projective geometry, omitting the basic notion of measurement...
, absolute geometry
Absolute geometry
Absolute geometry is a geometry based on an axiom system for Euclidean geometry that does not assume the parallel postulate or any of its alternatives. The term was introduced by János Bolyai in 1832...
, affine geometry
Affine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
, Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, and hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. For each of these geometries there are many different and inequivalent systems of axioms for various dimensions. Some of these axiom systems include "completeness" axioms that are not first order.
As a typical example, the axioms for projective geometry use 2 types, points and lines, and a binary incidence relation between points and lines. If point and line variables are indicated by small and capital letter, and a incident to A is written as aA, then one set of axioms is
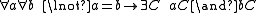(There is a line through any 2 distinct points a,b ...)
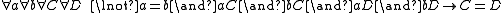(... which is unique)
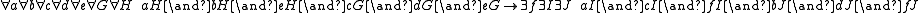(Veblen's axiom: if ab and cd lie on intersecting lines, then so do ac and bd.)
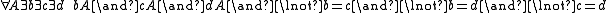(Every line has at least 3 points)
Euclid did not state all the axioms for Euclidean geometry explicitly, and the first complete list was given by Hilbert in Hilbert's axioms
Hilbert's axioms
Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book Grundlagen der Geometrie , as the foundation for a modern treatment of Euclidean geometry...
. This is not a first order axiomatization as one of Hilbert's axioms is a second order completeness axiom. Tarski's axioms
Tarski's axioms
Tarski's axioms, due to Alfred Tarski, are an axiom set for the substantial fragment of Euclidean geometry, called "elementary," that is formulable in first-order logic with identity, and requiring no set theory . Other modern axiomizations of Euclidean geometry are those by Hilbert and George...
are a first order axiomatization of Euclidean geometry. Tarski showed this axiom system is complete and decidable by relating it to the complete and decidable theory of real closed fields.
Differential algebra
- The theory DF of differential fields.
The signature is that of fields (0, 1, +, -, ×) together with a unary function ∂, the derivation.
The axioms are those for fields together with
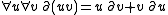
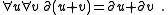
For this theory one can add the condition that the characteristic is p, a prime or zero,
to get the theory DFp of differential fields of characteristic p (and similarly with the other theories below).
If K is a differential field then the field of constants
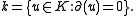
The theory of differentially perfect fields is the theory of differential fields together with the condition that the field of constants is perfect; in other words for each prime p it has the axiom:
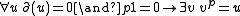
(There is little point in demanding that the whole field should be perfect field
Perfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
, because in non-zero characteristic this implies the differential is 0.)
For technical reasons to do with quantifier elimination
Quantifier elimination
Quantifier elimination is a concept of simplification used in mathematical logic, model theory, and theoretical computer science. One way of classifying formulas is by the amount of quantification...
it is sometimes more convenient to force the constant field to be perfect by adding a new symbol r to the signature with the axioms
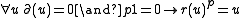
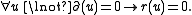
- The theory of DCF differentially closed fieldDifferentially closed fieldIn mathematics, a differential field K is differentially closed if every finite system of differential equations with a solution in some differential field extending K already has a solution in K. This concept was introduced by...
s is the theory of differentially perfect fields with axioms saying that such that if f and g are differential polynomials and the separant of f is nonzero and g≠0 and f has order greater than that of g, then there is some x in the field with f(x)=0 and g(x)≠0.
Addition
The theory of the natural numbers with a successor function has signature consisting of a constant 0 and a unary function S ("successor": S(x) is interpreted as x+1), and has axioms:- ∀x ¬ Sx = 0
- ∀x∀y Sx = Sy → x = y
- Let P(x) be a first-order formulaFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
with a single free variable x. Then the following formula is an axiom: ∧ ∀x(P(x)→P(Sx))) → ∀y P(y).
The last axiom (induction) can be replaced by the axioms
- For each integer n>0, the axiom ∀x SSS...Sx ≠ x (with n copies of S)
- ∀x ¬ x = 0 → ∃y Sy = x
The theory of the natural numbers with a successor function is complete and decidable, and is κ-categorical for uncountable κ but not for countable κ.
Presburger arithmetic
Presburger arithmetic
Presburger arithmetic is the first-order theory of the natural numbers with addition, named in honor of Mojżesz Presburger, who introduced it in 1929. The signature of Presburger arithmetic contains only the addition operation and equality, omitting the multiplication operation entirely...
is the theory of the natural numbers under addition, with signature consisting of a constant 0, a unary function, S, and a binary function +. It is complete and decidable. The axioms are
- ∀x ¬ Sx = 0
- ∀x∀y Sx = Sy → x = y
- ∀x x + 0 = x
- ∀x∀y x + Sy = S(x + y)
- Let P(x) be a first-order formulaFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
with a single free variable x. Then the following formula is an axiom: ∧ ∀x(P(x)→P(Sx))) → ∀y P(y).
Arithmetic
Many of the first order theories described above can be extended to complete recursively enumerable consistent theories. This is no longer true for most of the following theories; they can usually encode both multiplication and addition of natural numbers, and this gives them enough power to encode themselves, which implies that Gödel's incompleteness theorem applies and the theories can no longer be both complete and recursively enumerable (unless they are inconsistent).The signature of a theory of arithmetic has:
- The constant 0;
- The unary functionUnary functionA unary function is a function that takes one argument. In computer science, a unary operator is a subset of unary function.Many of the elementary functions are unary functions, in particular the trigonometric functions and hyperbolic function are unary....
, the successor function, here denoted by prefix S, or by prefix σ or postfix ′ elsewhere; - Two binary functionBinary functionIn mathematics, a binary function, or function of two variables, is a function which takes two inputs.Precisely stated, a function f is binary if there exists sets X, Y, Z such that\,f \colon X \times Y \rightarrow Z...
s, denoted by infix + and ×, called "addition" and "multiplication."
Some authors take the signature to contain a constant 1 instead of the function S, then define S in the obvious way as St = 1 + t.
Robinson arithmetic
Robinson arithmetic
In mathematics, Robinson arithmetic, or Q, is a finitely axiomatized fragment of Peano arithmetic , first set out in R. M. Robinson . Q is essentially PA without the axiom schema of induction. Since Q is weaker than PA, it is incomplete...
(also called Q). Axioms (1) and (2) govern the distinguished element 0. (3) assures that S is an injection
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
. Axioms (4) and (5) are the standard recursive definition of addition; (6) and (7) do the same for multiplication. Robinson arithmetic can be thought of as Peano arithmetic without induction. Q is a weak theory for which Gödel's incompleteness theorem
Gödel's incompleteness theorems
Gödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
holds.
Axioms:
- ∀x ¬ Sx = 0
- ∀x ¬ x = 0 → ∃y Sy = x
- ∀x∀y Sx = Sy → x = y
- ∀x x + 0 = x
- ∀x∀y x + Sy = S(x + y)
- ∀x x × 0 = 0
- ∀x∀y x × Sy = (x × y) + x.
IΣn is first order Peano arithmetic with induction restricted to Σn formulas
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
(for n = 0, 1, 2, ...). The theory IΣ0 is often denoted by IΔ0. This is a series of more and more powerful fragments of Peano arithmetic. The case n = 1 has about the same strength as primitive recursive arithmetic
Primitive recursive arithmetic
Primitive recursive arithmetic, or PRA, is a quantifier-free formalization of the natural numbers. It was first proposed by Skolem as a formalization of his finitist conception of the foundations of arithmetic, and it is widely agreed that all reasoning of PRA is finitist...
(PRA).
Exponential function arithmetic (EFA) is IΣ0 with an axiom stating that xy exists for all x and y (with the usual properties).
First order Peano arithmetic, PA. The "standard" theory of arithmetic. The axioms are the axioms of Robinson arithmetic
Robinson arithmetic
In mathematics, Robinson arithmetic, or Q, is a finitely axiomatized fragment of Peano arithmetic , first set out in R. M. Robinson . Q is essentially PA without the axiom schema of induction. Since Q is weaker than PA, it is incomplete...
above, together with the axiom scheme of induction:
-
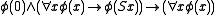for any formula φ in the language of PA. φ may contain free variables other than x.
Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
's 1931 paper proved that PA is incomplete, and has no consistent recursively enumerable completions.
Complete arithmetic (also known as true arithmetic) is the theory of the standard model of arithmetic, the natural numbers N. It is complete but does not have a recursively enumerable set of axioms.
Second order arithmetic
Second-order arithmeticSecond-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
can refer to a first order theory (in spite of the name) with two types of variables, thought of as varying over integers and subsets of the integers. (There is also a theory of arithmetic in second order logic that is called second order arithmetic. It has only one model, unlike the corresponding theory in first order logic, which is incomplete.) The signature will typically be the signature 0, S, +, × of arithmetic, together with a membership relation ∈ between integers and subsets (though there are numerous minor variations). The axioms are those of Robinson arithmetic
Robinson arithmetic
In mathematics, Robinson arithmetic, or Q, is a finitely axiomatized fragment of Peano arithmetic , first set out in R. M. Robinson . Q is essentially PA without the axiom schema of induction. Since Q is weaker than PA, it is incomplete...
, together with axiom schemes of induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
and comprehension
Axiom schema of specification
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axioms in Zermelo-Fraenkel set theory...
.
There are many different subtheories of second order arithmetic that differ in which formulas are allowed in the induction and comprehension schemes.
In order of increasing strength, five of the most common systems
are
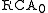, Recursive Comprehension
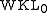, Weak König's lemma
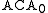, Arithmetical comprehension
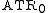, Arithmetical Transfinite Recursion
, 
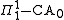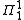comprehension
These are defined in detail in the articles on second order arithmetic and reverse mathematics
Reverse mathematics
Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...
.
Set theories
The usual signature of set theory has one binary relation ∈, no constants, and no functions. Some of the theories below are "class theories" which have two sorts of object, sets and classes. There are three common ways of handling this in first-order logic:- Use first-order logic with two types.
- Use ordinary first-order logic, but add a new unary predicate "Set", where "Set(t)" means informally "t is a set".
- Use ordinary first-order logic, and instead of adding a new predicate to the language, treat "Set(t)" as an abbreviation for "∃y t∈y"
Some first order set theories include:
- Weak theories lacking powersets:
- S'General set theoryGeneral set theory is George Boolos's name for a fragment of the axiomatic set theory Z. GST is sufficient for all mathematics not requiring infinite sets, and is the weakest known set theory whose theorems include the Peano axioms.-Ontology:...
(Tarski, Mostowksi, and Robinson, 1953); (finitely axiomatizable) - General set theoryGeneral set theoryGeneral set theory is George Boolos's name for a fragment of the axiomatic set theory Z. GST is sufficient for all mathematics not requiring infinite sets, and is the weakest known set theory whose theorems include the Peano axioms.-Ontology:...
; - Kripke-Platek set theory;
- S'
- Zermelo set theoryZermelo set theoryZermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
; - Ackermann set theoryAckermann set theoryAckermann set theory is a version of axiomatic set theory proposed by Wilhelm Ackermann in 1956.- The language:Ackermann set theory is formulated in first-order logic. The language L_A consists of one binary relation \in and one constant V . We will write x \in y for \in...
- Zermelo-Fraenkel set theory;
- Von Neumann-Bernays-Gödel set theory; (finitely axiomatizable)
- Morse–Kelley set theoryMorse–Kelley set theoryIn the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...
; - New FoundationsNew FoundationsIn mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
; (finitely axiomatizable) - Scott-Potter set theory
- Positive set theory
Some extra first order axioms that can be added to one of these (usually ZF) include:
- axiom of choice, axiom of dependent choiceAxiom of dependent choiceIn mathematics, the axiom of dependent choices, denoted DC, is a weak form of the axiom of choice which is still sufficient to develop most of real analysis...
- Generalized continuum hypothesis
- Martin's axiomMartin's axiomIn the mathematical field of set theory, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH...
(usually together with the negation of the continuum hypothesis), Martin's maximumMartin's maximumIn set theory, Martin's maximum, introduced by , is a generalization of the proper forcing axiom, which is in turn a generalization of Martin's axiom.... - ◊DiamondsuitIn mathematics, and particularly in axiomatic set theory, the diamond principle ◊ is a combinatorial principle introduced by that holds in the constructible universe and that implies the continuum hypothesis...
and ♣ClubsuitIn mathematics, and particularly in axiomatic set theory, ♣S is a family of combinatorial principles that are weaker version of the corresponding ◊S; it was introduced in 1975 by A... - Axiom of constructibilityAxiom of constructibilityThe axiom of constructibility is a possible axiom for set theory in mathematics that asserts that every set is constructible. The axiom is usually written as V = L, where V and L denote the von Neumann universe and the constructible universe, respectively.- Implications :The axiom of...
(V=L) - proper forcing axiomProper Forcing AxiomIn the mathematical field of set theory, the proper forcing axiom is a significant strengthening of Martin's axiom, where forcings with the countable chain condition are replaced by proper forcings.- Statement :...
- analytic determinacy, projective determinacy, Axiom of determinacyAxiom of determinacyThe axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
- Many large cardinal axioms