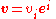Covariance and contravariance
Encyclopedia
In multilinear algebra
and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis
from one coordinate system
to another. When one coordinate system is just a rotation
of the other, this distinction is invisible. However, when considering more general coordinate systems such as skew coordinates
, curvilinear coordinates
, and coordinate systems on differentiable manifold
s, the distinction becomes critically important.
In physics, vectors often have units of distance or distance times some other unit (such as the velocity), whereas covectors have units the inverse of distance or the inverse of distance times some other unit. The distinction between covariant and contravariant vectors is particularly important for computations with tensor
s, which often have mixed variance. This means that they have both covariant and contravariant components, or both vectors and dual vectors. The valence or type of a tensor is the number of variant and covariant terms. The duality between covariance and contravariance intervenes whenever a vector or tensor quantity is represented by its components, although modern differential geometry uses more sophisticated index-free methods to represent tensors.
The terms covariant and contravariant were introduced by J.J. Sylvester in 1853 in order to study algebraic invariant theory
. In this context, for instance, a system of simultaneous equations
is contravariant in the variables. The use of both terms in the modern context of multilinear algebra
is a specific example of corresponding notions in category theory
.
) of numbers such as
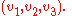
This list of numbers depends on the choice of coordinate system
. For instance, if the vector represents position with respect to an observer (position vector), then the coordinate system may be obtained from a system of rigid rods, or reference axes, along which the components v1, v2, and v3 are measured. For a vector to represent a geometric object, it must be possible to describe how it looks in any other coordinate system. That is to say, the components of the vectors will transform in a certain way in passing from one coordinate system to another.
A contravariant vector is required to have components that "transform in the same way as the coordinates" (the opposite way as the reference axes) under changes of coordinates such as rotation
and dilation. The vector itself does not change under these operations; instead, the components of the vector make a change that cancels the change in the spatial axes, in the same way that co-ordinates change. In other words, if the reference axes were rotated in one direction, the component representation of the vector would rotate in exactly the opposite way. Similarly, if the reference axes were stretched in one direction, the components of the vector, like the co-ordinates, would reduce in an exactly compensating way. Mathematically, if the coordinate system undergoes a transformation described by an invertible matrix M, so that a coordinate vector x is transformed to x′ = Mx, then a contravariant vector v must be similarly transformed via v′ = Mv. This important requirement is what distinguishes a contravariant vector from any other triple of physically meaningful quantities. For example, if v consists of the x, y, and z-components of velocity
, then v is a contravariant vector: if the coordinates of space are stretched, rotated, or twisted, then the components of the velocity transform in the same way. On the other hand, for instance, a triple consisting of the length, width, and height of a rectangular box could make up the three components of an abstract vector
, but this vector would not be contravariant, since rotating the box does not change the box's length, width, and height. Examples of contravariant vectors include displacement
, velocity
, momentum
, force, and acceleration
.
By contrast, a covariant vector has components that change oppositely to the coordinates or, equivalently, transform like the reference axes. For instance, the components of the gradient
vector of a function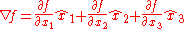
transform like the reference axes themselves. When only rotations
of the spatial are considered, the components of contravariant and covariant vectors behave in the same way. It is only when other transformations are allowed that the difference becomes apparent.
transform under a change of basis
(passive transformation
). Thus let V be a vector space
of dimension n over the field of scalars
S, and let each of f = (X1,...,Xn) and f' = (Y1,...,Yn) be a basis of V.A basis f may here profitably be viewed as a linear isomorphism from Rn to V. Regarding f as a row vector whose entries are the elements of the basis, the associated linear isomorphism is then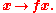 Also, let the change of basis
Also, let the change of basis
from f to f′ be given by
for some invertible n×n matrix A with entries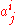 .
.
Here, each vector Yj of the f' basis is a linear combination of the vectors Xi of the f basis, so that
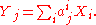
v in V is expressed uniquely as a linear combination
of the elements of the f basis as
where v i[f] are scalar
s in S known as the components of v in the f basis. Denote the column vector of components of v by v[f]:
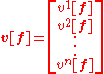
so that can be rewritten as a matrix product
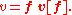
The vector v may also be expressed in terms of the f' basis, so that
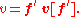
However, since the vector v itself is invariant under the choice of basis,
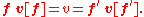
The invariance of v combined with the relationship between f and f' implies that
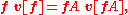
giving the transformation rule
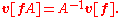
In terms of components,

where the coefficients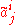 are the entries of the inverse matrix of A.
are the entries of the inverse matrix of A.
Because the components of the vector v transform with the inverse of the matrix A, these components are said to transform contravariantly under a change of basis.
The way A relates the two pairs is depicted in the following informal diagram using an arrow. The reversal of the arrow indicates a contravariant change: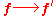

α on V is expressed uniquely in terms of its components (scalars in S) in the f basis as
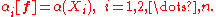
These components are the action of α on the basis vectors Xi of the f basis.
Under the change of basis from f to f' , the components transform so that
Denote the row vector of components of α by α[f]:
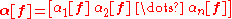
so that can be rewritten as the matrix product

Because the components of the linear functional α transform with the matrix A, these components are said to transform covariantly under a change of basis.
The way A relates the two pairs is depicted in the following informal diagram using an arrow. A covariant relationship is indicated since the arrows travel in the same direction: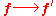

Had a column vector representation been used instead, the transformation law would be the transpose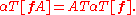

The coordinates on V are therefore contravariant in the sense that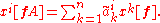
Conversely, a system of n quantities vi that transform like the coordinates xi on V defines a contravariant vector. A system of n quantities that transform oppositely to the coordinates is then a covariant vector.
This formulation of contravariance and covariance is often more natural in applications in which there is a coordinate space (a manifold
) on which vectors live as tangent vector
s or cotangent vectors. Given a local coordinate system xi on the manifold, the reference axes for the coordinate system are the vector field
s
This gives rise to the frame f = (X1,...,Xn) at every point of the coordinate patch.
If yi is a different coordinate system and
then the frame f' is related to the frame f by the inverse of the Jacobian matrix of the coordinate transition:
Or, in indices,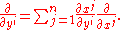
A tangent vector
is by definition a vector that is a linear combination of the coordinate partials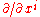 . Thus a tangent vector is defined by
. Thus a tangent vector is defined by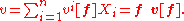
Such a vector is contravariant with respect to change of frame. Under changes in the coordinate system, one has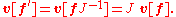
Therefore the components of a tangent vector transform via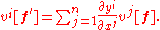
Accordingly, a system of n quantities vi depending on the coordinates that transform in this way on passing from one coordinate system to another is called a contravariant vector.
V, there is little distinction between covariant and contravariant vectors, because the dot product
allows for covectors to be identified with vectors. That is, a vector v determines uniquely a covector α via
for all vectors w. Conversely, each covector α determines a unique vector v by this equation. Because of this identification of vectors with covectors, one may speak of the covariant components or contravariant components of a vector, that is, they are just representations of the same vector using reciprocal bases.
Given a basis f = (X1,...,Xn) of V, there is a unique reciprocal basis f# = (Y1,...,Yn) of V determined by requiring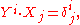
the Kronecker delta. In terms of these bases, any vector v can be written in two ways: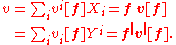
The components vi[f] are the contravariant components of the vector v in the basis f, and the components vi[f] are the covariant components of v in the basis f. The terminology is justified because under a change of basis,
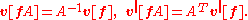
allows for vectors to be identified with vectors. If is a basis, then the dual basis
is a basis, then the dual basis 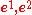 satisfies
satisfies
Thus, e1 and e2 are perpendicular to each other, as are e2 and e1, and the lengths of e1 and e2 normalized against e1 and e2, respectively.
Applying these rules, we find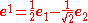
and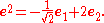
Thus the change of basis matrix in going from the original basis to the reciprocal basis is
since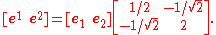
For instance, the vector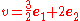
is a vector with contravariant components
The covariant components are obtained by equating the two expressions for the vector v: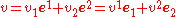
so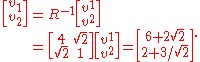
, one can also determine explicitly the dual basis to a given set of basis vectors e1, e2, e3 of E3 that are not necessarily assumed to be orthogonal nor of unit norm. The contravariant (dual) basis vectors are:

Even when the ei and ei are not orthonormal
, they are still mutually dual: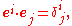
Then the contravariant coordinates of any vector v can be obtained by the dot product
of v with the contravariant basis vectors:

Likewise, the covariant components of v can be obtained from the dot product of v with covariant basis vectors, viz.

Then v can be expressed in two (reciprocal) ways, viz.
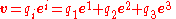
or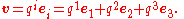
Combining the above relations, we have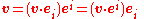
and we can convert from covariant to contravariant basis with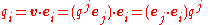
and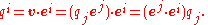
The indices of covariant coordinates, vectors, and tensors are subscripts. If the contravariant basis vectors are orthonormal then they are equivalent to the covariant basis vectors, so there is no need to distinguish between the covariant and contravariant coordinates.
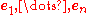 ,
,
the reciprocal basis is given by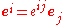
where the coefficients eij are the entries of the inverse matrix of
Indeed, we then have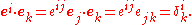
The covariant and contravariant components of any vector
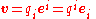
are related as above by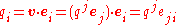
and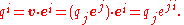
, the adjective
covariant is often used informally as a synonym for invariant
. For example, the Schrödinger equation
does not keep its written form under the coordinate transformations of special relativity
. Thus, a physicist might say that the Schrödinger equation is not covariant. In contrast, the Klein-Gordon equation
and the Dirac equation
do keep their written form under these coordinate transformations. Thus, a physicist might say that these equations are covariant.
Despite the dominant usage of "covariant", it is more accurate to say that the Klein-Gordon and Dirac equations are invariant, and that the Schrödinger equation is not invariant. Additionally, to remove ambiguity, the transformation by which the invariance is evaluated should be indicated. Continuing with the above example, neither the Klein-Gordon nor the Dirac equations are universally invariant under any coordinate transformation (e.g. those of general relativity
), so unambiguous description of these equations is that they are invariant with respect to the coordinate transformations of special relativity.
Because the components of vectors are contravariant and those of covectors are covariant, the vectors themselves are often referred to as being contravariant and the covectors as covariant. This usage is not universal, however, since vectors push forward – are covariant under diffeomorphism
– and covectors pull back – are contravariant under diffeomorphism. See Einstein notation for details.
s, which often have mixed variance. This means that they have both covariant and contravariant components, or both vector and dual vector components. The valence of a tensor is the number of variant and covariant terms, and in Einstein notation
, covariant components have lower indices, while contravariant components have upper indices. The duality between covariance and contravariance intervenes whenever a vector or tensor quantity is represented by its components, although modern differential geometry uses more sophisticated index-free methods to represent tensors
.
In tensor analysis, a covariant vector varies more or less reciprocally to a corresponding contravariant vector. Expressions for lengths, areas and volumes of objects in the vector space can then be given in terms of tensors with covariant and contravariant indices. Under simple expansions and contractions of the coordinates, the reciprocity is exact; under affine transformations the components of a vector intermingle on going between covariant and contravariant expression.
On a manifold
, a tensor field
will typically have multiple indices, of two sorts. By a widely followed convention, covariant indices are written as lower indices, whereas contravariant indices are upper indices. When the manifold is equipped with a metric
, covariant and contravariant indices become very closely related to one-another. Contravariant indices can be turned into covariant indices by contracting with the metric tensor. Contravariant indices can be gotten by contracting with the (matrix) inverse of the metric tensor. Note that in general, no such relation exists in spaces not endowed with a metric tensor. Furthermore, from a more abstract standpoint, a tensor is simply "there" and its components of either kind are only calculational artifacts whose values depend on the chosen coordinates.
The explanation in geometric terms is that a general tensor will have contravariant indices as well as covariant indices, because it has parts that live in the tangent bundle
as well as the cotangent bundle
.
A contravariant vector is one which transforms like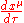 , where
, where 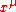 are the coordinates of a particle at its proper time
are the coordinates of a particle at its proper time
 . A covariant vector is one which transforms like
. A covariant vector is one which transforms like 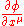 , where
, where  is a scalar field.
is a scalar field.
, there are covariant functors and contravariant functors. The dual space
of a vector space is a standard example of a contravariant functor. Some constructions of multilinear algebra
are of 'mixed' variance, which prevents them from being functors.
In geometry
, the same map in/map out distinction is helpful in assessing the variance of constructions. A tangent vector
to a smooth manifold M is, to begin with, a curve
mapping smoothly into M and passing through a given point P. It is therefore covariant, with respect to smooth mappings of M. A contravariant vector, or 1-form, is in the same way constructed from a smooth mapping from M to the real line, near P. It is in the cotangent bundle
, built up from the dual space
s of the tangent space
s. Its components with respect to a local basis of one-forms dxi will be covariant; but one-forms and differential form
s in general are contravariant, in the sense that they pull back under smooth mappings. This is crucial to how they are applied; for example a differential form can be restricted to any submanifold
, while this does not make the same sense for a field of tangent vectors.
Covariant and contravariant components transform in different ways under coordinate transformations
. By considering a coordinate transformation on a manifold as a map from the manifold to itself, the transformation of covariant indices of a tensor are given by a pullback, and the transformation properties of the contravariant indices is given by a pushforward.
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis
Change of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
from one coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
to another. When one coordinate system is just a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
of the other, this distinction is invisible. However, when considering more general coordinate systems such as skew coordinates
Skew coordinates
A system of skew coordinates is a coordinate system where the coordinate surfaces are not orthogonal, in contrast to orthogonal coordinates.Skew coordinates tend to be more complicated to work with compared to orthogonal coordinates since the metric tensor will have nonzero off-diagonal components,...
, curvilinear coordinates
Curvilinear coordinates
Curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
, and coordinate systems on differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s, the distinction becomes critically important.
- For a vector (such as a direction vector or velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
vector) to be coordinate system invariant, the components of the vector must contra-vary with a change of basis to compensate. That is, the components must vary in the opposite way (the inverse transformation) as the change of basis. Vectors (as opposed to dual vectors) are said to be contravariant. Examples of contravariant vectors include the position of an object relative to an observer, or any derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of position with respect to time, including velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, accelerationAccelerationIn physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
, and jerk. In Einstein notationEinstein notationIn mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
, contravariant components have upper indices as in
- For a dual vector, (such as a gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
) to be coordinate system invariant, the components of the vector must co-vary with a change of basis to maintain the same meaning. That is, the components must vary by the same transformation as the change of basis. Dual vectors (as opposed to vectors) are said to be covariant. Examples of covariant vectors generally appear when taking a gradient of a function (effectively dividing by a vector). In Einstein notationEinstein notationIn mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
, covariant components have lower indices as in
In physics, vectors often have units of distance or distance times some other unit (such as the velocity), whereas covectors have units the inverse of distance or the inverse of distance times some other unit. The distinction between covariant and contravariant vectors is particularly important for computations with tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s, which often have mixed variance. This means that they have both covariant and contravariant components, or both vectors and dual vectors. The valence or type of a tensor is the number of variant and covariant terms. The duality between covariance and contravariance intervenes whenever a vector or tensor quantity is represented by its components, although modern differential geometry uses more sophisticated index-free methods to represent tensors.
The terms covariant and contravariant were introduced by J.J. Sylvester in 1853 in order to study algebraic invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
. In this context, for instance, a system of simultaneous equations
Simultaneous equations
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
is contravariant in the variables. The use of both terms in the modern context of multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
is a specific example of corresponding notions in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
.
Introduction
In physics, a vector typically arises as the outcome of a measurement or series of measurements, and is represented as a list (or tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
) of numbers such as
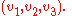
This list of numbers depends on the choice of coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
. For instance, if the vector represents position with respect to an observer (position vector), then the coordinate system may be obtained from a system of rigid rods, or reference axes, along which the components v1, v2, and v3 are measured. For a vector to represent a geometric object, it must be possible to describe how it looks in any other coordinate system. That is to say, the components of the vectors will transform in a certain way in passing from one coordinate system to another.
A contravariant vector is required to have components that "transform in the same way as the coordinates" (the opposite way as the reference axes) under changes of coordinates such as rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
and dilation. The vector itself does not change under these operations; instead, the components of the vector make a change that cancels the change in the spatial axes, in the same way that co-ordinates change. In other words, if the reference axes were rotated in one direction, the component representation of the vector would rotate in exactly the opposite way. Similarly, if the reference axes were stretched in one direction, the components of the vector, like the co-ordinates, would reduce in an exactly compensating way. Mathematically, if the coordinate system undergoes a transformation described by an invertible matrix M, so that a coordinate vector x is transformed to x′ = Mx, then a contravariant vector v must be similarly transformed via v′ = Mv. This important requirement is what distinguishes a contravariant vector from any other triple of physically meaningful quantities. For example, if v consists of the x, y, and z-components of velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, then v is a contravariant vector: if the coordinates of space are stretched, rotated, or twisted, then the components of the velocity transform in the same way. On the other hand, for instance, a triple consisting of the length, width, and height of a rectangular box could make up the three components of an abstract vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, but this vector would not be contravariant, since rotating the box does not change the box's length, width, and height. Examples of contravariant vectors include displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
, velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, force, and acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
.
By contrast, a covariant vector has components that change oppositely to the coordinates or, equivalently, transform like the reference axes. For instance, the components of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
vector of a function
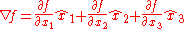
transform like the reference axes themselves. When only rotations
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
of the spatial are considered, the components of contravariant and covariant vectors behave in the same way. It is only when other transformations are allowed that the difference becomes apparent.
Definition
The general formulation of covariance and contravariance refers to how the components of a coordinate vectorCoordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
transform under a change of basis
Change of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
(passive transformation
Active and passive transformation
In the physical sciences, an active transformation is one which actually changes the physical position of a system, and makes sense even in the absence of a coordinate system whereas a passive transformation is a change in the coordinate description of the physical system . The distinction between...
). Thus let V be a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of dimension n over the field of scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
S, and let each of f = (X1,...,Xn) and f' = (Y1,...,Yn) be a basis of V.A basis f may here profitably be viewed as a linear isomorphism from Rn to V. Regarding f as a row vector whose entries are the elements of the basis, the associated linear isomorphism is then
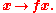 Also, let the change of basis
Also, let the change of basisChange of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
from f to f′ be given by
for some invertible n×n matrix A with entries
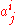 .
.Here, each vector Yj of the f' basis is a linear combination of the vectors Xi of the f basis, so that
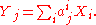
Contravariant transformation
A vectorCoordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
v in V is expressed uniquely as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the elements of the f basis as
where v i[f] are scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
s in S known as the components of v in the f basis. Denote the column vector of components of v by v[f]:
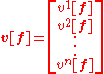
so that can be rewritten as a matrix product
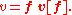
The vector v may also be expressed in terms of the f' basis, so that
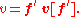
However, since the vector v itself is invariant under the choice of basis,
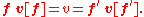
The invariance of v combined with the relationship between f and f' implies that
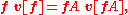
giving the transformation rule
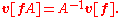
In terms of components,

where the coefficients
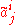 are the entries of the inverse matrix of A.
are the entries of the inverse matrix of A.Because the components of the vector v transform with the inverse of the matrix A, these components are said to transform contravariantly under a change of basis.
The way A relates the two pairs is depicted in the following informal diagram using an arrow. The reversal of the arrow indicates a contravariant change:
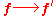

Covariant transformation
A linear functionalLinear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
α on V is expressed uniquely in terms of its components (scalars in S) in the f basis as
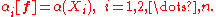
These components are the action of α on the basis vectors Xi of the f basis.
Under the change of basis from f to f' , the components transform so that
Denote the row vector of components of α by α[f]:
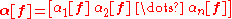
so that can be rewritten as the matrix product

Because the components of the linear functional α transform with the matrix A, these components are said to transform covariantly under a change of basis.
The way A relates the two pairs is depicted in the following informal diagram using an arrow. A covariant relationship is indicated since the arrows travel in the same direction:
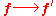

Had a column vector representation been used instead, the transformation law would be the transpose
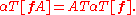
Coordinates
The choice of basis f on the vector space V defines uniquely a set of coordinate functions on V, by means of
The coordinates on V are therefore contravariant in the sense that
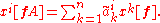
Conversely, a system of n quantities vi that transform like the coordinates xi on V defines a contravariant vector. A system of n quantities that transform oppositely to the coordinates is then a covariant vector.
This formulation of contravariance and covariance is often more natural in applications in which there is a coordinate space (a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
) on which vectors live as tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s or cotangent vectors. Given a local coordinate system xi on the manifold, the reference axes for the coordinate system are the vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s

This gives rise to the frame f = (X1,...,Xn) at every point of the coordinate patch.
If yi is a different coordinate system and

then the frame f' is related to the frame f by the inverse of the Jacobian matrix of the coordinate transition:

Or, in indices,
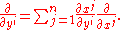
A tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
is by definition a vector that is a linear combination of the coordinate partials
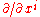 . Thus a tangent vector is defined by
. Thus a tangent vector is defined by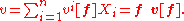
Such a vector is contravariant with respect to change of frame. Under changes in the coordinate system, one has
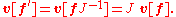
Therefore the components of a tangent vector transform via
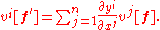
Accordingly, a system of n quantities vi depending on the coordinates that transform in this way on passing from one coordinate system to another is called a contravariant vector.
Covariant and contravariant components of a vector
In a Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
V, there is little distinction between covariant and contravariant vectors, because the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
allows for covectors to be identified with vectors. That is, a vector v determines uniquely a covector α via

for all vectors w. Conversely, each covector α determines a unique vector v by this equation. Because of this identification of vectors with covectors, one may speak of the covariant components or contravariant components of a vector, that is, they are just representations of the same vector using reciprocal bases.
Given a basis f = (X1,...,Xn) of V, there is a unique reciprocal basis f# = (Y1,...,Yn) of V determined by requiring
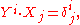
the Kronecker delta. In terms of these bases, any vector v can be written in two ways:
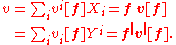
The components vi[f] are the contravariant components of the vector v in the basis f, and the components vi[f] are the covariant components of v in the basis f. The terminology is justified because under a change of basis,
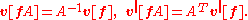
Euclidean plane
In the Euclidean plane, the dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
allows for vectors to be identified with vectors. If
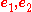 is a basis, then the dual basis
is a basis, then the dual basis 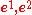 satisfies
satisfies
Thus, e1 and e2 are perpendicular to each other, as are e2 and e1, and the lengths of e1 and e2 normalized against e1 and e2, respectively.
Example
For example, suppose that we are given a basis e1, e2 consisting of a pair of vectors making a 45° angle with one another, such that e1 has length 2 and e2 has length 1. Then the dual basis vectors are given as follows:- e2 is the result of rotating e1 through an angle of 90° (where the sense is measured by assuming the pair e1, e2 to be positively oriented), and then rescaling so that holds.
- e1 is the result of rotating e2 through an angle of 90°, and then rescaling so that holds.
Applying these rules, we find
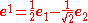
and
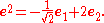
Thus the change of basis matrix in going from the original basis to the reciprocal basis is

since
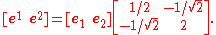
For instance, the vector
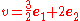
is a vector with contravariant components

The covariant components are obtained by equating the two expressions for the vector v:
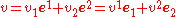
so
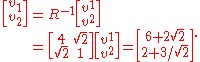
Three-dimensional Euclidean space
In the three-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, one can also determine explicitly the dual basis to a given set of basis vectors e1, e2, e3 of E3 that are not necessarily assumed to be orthogonal nor of unit norm. The contravariant (dual) basis vectors are:

Even when the ei and ei are not orthonormal
Orthonormality
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal and both of unit length. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length...
, they are still mutually dual:
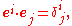
Then the contravariant coordinates of any vector v can be obtained by the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of v with the contravariant basis vectors:

Likewise, the covariant components of v can be obtained from the dot product of v with covariant basis vectors, viz.

Then v can be expressed in two (reciprocal) ways, viz.
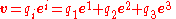
or
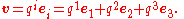
Combining the above relations, we have
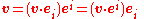
and we can convert from covariant to contravariant basis with
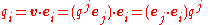
and
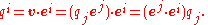
The indices of covariant coordinates, vectors, and tensors are subscripts. If the contravariant basis vectors are orthonormal then they are equivalent to the covariant basis vectors, so there is no need to distinguish between the covariant and contravariant coordinates.
General Euclidean spaces
More generally, in an n-dimensional Euclidean space V, if a basis is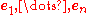 ,
,the reciprocal basis is given by
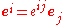
where the coefficients eij are the entries of the inverse matrix of

Indeed, we then have
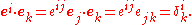
The covariant and contravariant components of any vector
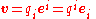
are related as above by
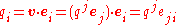
and
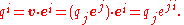
Informal usage
In the field of physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the adjective
Adjective
In grammar, an adjective is a 'describing' word; the main syntactic role of which is to qualify a noun or noun phrase, giving more information about the object signified....
covariant is often used informally as a synonym for invariant
Invariant (physics)
In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another...
. For example, the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
does not keep its written form under the coordinate transformations of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. Thus, a physicist might say that the Schrödinger equation is not covariant. In contrast, the Klein-Gordon equation
Klein-Gordon equation
The Klein–Gordon equation is a relativistic version of the Schrödinger equation....
and the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
do keep their written form under these coordinate transformations. Thus, a physicist might say that these equations are covariant.
Despite the dominant usage of "covariant", it is more accurate to say that the Klein-Gordon and Dirac equations are invariant, and that the Schrödinger equation is not invariant. Additionally, to remove ambiguity, the transformation by which the invariance is evaluated should be indicated. Continuing with the above example, neither the Klein-Gordon nor the Dirac equations are universally invariant under any coordinate transformation (e.g. those of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
), so unambiguous description of these equations is that they are invariant with respect to the coordinate transformations of special relativity.
Because the components of vectors are contravariant and those of covectors are covariant, the vectors themselves are often referred to as being contravariant and the covectors as covariant. This usage is not universal, however, since vectors push forward – are covariant under diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
– and covectors pull back – are contravariant under diffeomorphism. See Einstein notation for details.
Use in tensor analysis
The distinction between covariance and contravariance is particularly important for computations with tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s, which often have mixed variance. This means that they have both covariant and contravariant components, or both vector and dual vector components. The valence of a tensor is the number of variant and covariant terms, and in Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
, covariant components have lower indices, while contravariant components have upper indices. The duality between covariance and contravariance intervenes whenever a vector or tensor quantity is represented by its components, although modern differential geometry uses more sophisticated index-free methods to represent tensors
Tensor (intrinsic definition)
In mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multi-linear concept...
.
In tensor analysis, a covariant vector varies more or less reciprocally to a corresponding contravariant vector. Expressions for lengths, areas and volumes of objects in the vector space can then be given in terms of tensors with covariant and contravariant indices. Under simple expansions and contractions of the coordinates, the reciprocity is exact; under affine transformations the components of a vector intermingle on going between covariant and contravariant expression.
On a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, a tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
will typically have multiple indices, of two sorts. By a widely followed convention, covariant indices are written as lower indices, whereas contravariant indices are upper indices. When the manifold is equipped with a metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
, covariant and contravariant indices become very closely related to one-another. Contravariant indices can be turned into covariant indices by contracting with the metric tensor. Contravariant indices can be gotten by contracting with the (matrix) inverse of the metric tensor. Note that in general, no such relation exists in spaces not endowed with a metric tensor. Furthermore, from a more abstract standpoint, a tensor is simply "there" and its components of either kind are only calculational artifacts whose values depend on the chosen coordinates.
The explanation in geometric terms is that a general tensor will have contravariant indices as well as covariant indices, because it has parts that live in the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
as well as the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
.
A contravariant vector is one which transforms like
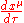 , where
, where 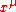 are the coordinates of a particle at its proper time
are the coordinates of a particle at its proper timeProper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
 . A covariant vector is one which transforms like
. A covariant vector is one which transforms like 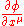 , where
, where  is a scalar field.
is a scalar field.Algebra and geometry
In category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, there are covariant functors and contravariant functors. The dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of a vector space is a standard example of a contravariant functor. Some constructions of multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
are of 'mixed' variance, which prevents them from being functors.
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the same map in/map out distinction is helpful in assessing the variance of constructions. A tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
to a smooth manifold M is, to begin with, a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
mapping smoothly into M and passing through a given point P. It is therefore covariant, with respect to smooth mappings of M. A contravariant vector, or 1-form, is in the same way constructed from a smooth mapping from M to the real line, near P. It is in the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
, built up from the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
s of the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s. Its components with respect to a local basis of one-forms dxi will be covariant; but one-forms and differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s in general are contravariant, in the sense that they pull back under smooth mappings. This is crucial to how they are applied; for example a differential form can be restricted to any submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
, while this does not make the same sense for a field of tangent vectors.
Covariant and contravariant components transform in different ways under coordinate transformations
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
. By considering a coordinate transformation on a manifold as a map from the manifold to itself, the transformation of covariant indices of a tensor are given by a pullback, and the transformation properties of the contravariant indices is given by a pushforward.
See also
- Covariant transformationCovariant transformationIn physics, a covariant transformation is a rule , that describes how certain physical entities change under a change of coordinate system....
- Change of basisChange of basisIn linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
- Active and passive transformationActive and passive transformationIn the physical sciences, an active transformation is one which actually changes the physical position of a system, and makes sense even in the absence of a coordinate system whereas a passive transformation is a change in the coordinate description of the physical system . The distinction between...
- Two-point tensorTwo-point tensorTwo-point tensors, or double vectors, are tensor-like quantities which transform as vectors with respect to each of their indices and are used in continuum mechanics to transform between reference and present coordinates...
, which generalizes this notion to tensors that have indices not just in the primal and dual space but in other vector spaces (such as other tangent spaces on the same manifold). - Mixed tensorMixed tensorIn tensor analysis, a mixed tensor is a tensor which is neither strictly covariant nor strictly contravariant; at least one of the indices of a mixed tensor will be a subscript and at least one of the indices will be a superscript ....