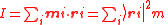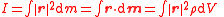Defining equation (physics)
Encyclopedia
In physics
, defining equations are equation
s that define new quantities in terms of base quantities. This article uses the current SI system
of units
, not natural
or characteristic units
.
The standard ordered vector basis for spherical polar coordinates; are used with the general forms of unit vectors below.
are used with the general forms of unit vectors below.
Common general themes of unit vectors occur throughout physics:
Every conservative force
has a potential energy
. By following two principles one can consistently assign a non-relative value to U:
- Wherever the force is zero, its potential energy is defined to be zero as well.
- Whenever the force does work, potential energy is lost.
 is a unit vector in the direction of the flow/current/flux.
is a unit vector in the direction of the flow/current/flux.
where the oscillations are parallel (or antiparallel) to the propagation direction, or transverse
where the oscillations are perpendicular to the propagation direction. These oscillations are characterized by a periodically time-varying displacement in the parallel or perpendicular direction, and so the instantaneous velocity and acceleration are also periodic and time varying in these directions. But the wave profile (the apparent motion of the wave due to the successive oscillations of particles or fields about their equilibrium positions) propagates at the phase and group velocities parallel or antiparallel to the propagation direction, which is common to longitudinal and transverse waves. Below oscillatory displacement, velocity and acceleration refer to the kinematics in the oscillating directions of the wave - transverse or longitudinal (mathematical description is identical), the group and phase velocities are separate.
Relation between space, time, angle analogues used to describe the phase:
. They are defined in similar ways but are not exactly the same quantity. Centre of mass is the mathematical descrition of placing all the mass in the region considered to one position, centre of gravity is a real physical quantity, the point of a body where the gravitational force acts. They are only equal if and only if the external gravitational field is uniform.
\sum_i \mathbf{m}_i \left | \mathbf{g} \left ( \mathbf{r}_i \right ) \right | \\
& = \frac{1}{M \left | \mathbf{g} \left ( \mathbf{r}_\mathrm{cog} \right ) \right |}\sum_i \mathbf{r}_i m_i \left | \mathbf{g} \left ( \mathbf{r}_i \right ) \right | \end{align}\,\!
Centre of a gravity for a continuum of mass:
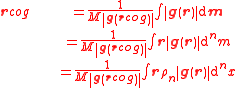
| m
| [L]
|-
|Standard gravitational parameter
of a mass
| μ
|
| N m2 kg−1
| [L]3 [T]−2
|-
|Gravitational field
, field strength, potential gradient, acceleration
| g
|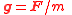
| N kg−1 = m s−2
| [L][T]−2
|-
|Gravitational flux
| ΦG
|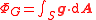
| m3 s−2
| [L]3[T]−2
|-
|Absolute gravitational potential
| Φ, φ, U, V
|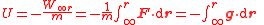
| J kg−1
| [L]2[T]−2
|-
|Gravitational potential difference
| ΔΦ, Δφ, ΔU, ΔV
|
| J kg−1
| [L]2[T]−2
|-
|Gravitational potential energy
|| Ep
|
| J
| [M][L]2[T]−2
|-
|Gravitational torsion field|| Ω
|
| Hz = s−1
| [T]−1
|-
|Gravitational torsion flux|| ΦΩ
|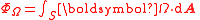
| N m s kg−1 = m2 s−1
| [M]2 [T]−1
|-
|Gravitomagnetic field
|| H, Bg, B, ξ
|
| Hz = s−1
| [T]−1
|-
|Gravitomagnetic flux
| Φξ
|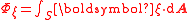
| N m s kg−1 = m2 s−1
| [M]2 [T]−1
|-
|Gravitomagnetic vector potential
| h
|
| m s−1
| [M] [T]−1
|-
|}
and electrostatics
, there are no "centre of charge" or "centre of electrostatic attraction" analogues.
Electric transport
Electric fields
Magnetic fields
AC circuits
, the most common are in terms of the E and B or E and H fields.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, defining equations are equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
s that define new quantities in terms of base quantities. This article uses the current SI system
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
of units
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
, not natural
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
or characteristic units
Nondimensionalization
Nondimensionalization is the partial or full removal of units from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis...
.
Treatment of vectors
There are many forms of vector notation. In this section the following is specifically used throughout the article, closely matching standard use; upright boldface is for a vector quantity and upright boldface with a hat (circumflex) is for a unit vector.The standard ordered vector basis for spherical polar coordinates;
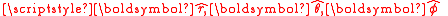 are used with the general forms of unit vectors below.
are used with the general forms of unit vectors below.Common general themes of unit vectors occur throughout physics:
| Unit vector | Nomenclature | Diagram |
|---|---|---|
| Tangent vector to a curve/flux line |  |
A normal vector  to the plane containing and defined by the radial position vector to the plane containing and defined by the radial position vector  and angular tangential direction of rotation and angular tangential direction of rotation  is necessary so that the vector equations of angular motion hold. is necessary so that the vector equations of angular motion hold. |
| Normal to a surface tangent plane/plane containing radial position component and angular tangential component |  In terms of polar coordinates Spherical coordinate system In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of... ; 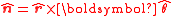 |
|
| Binormal vector to tangent and normal |  |
|
| Parallel to some axis/line | 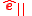 |
One unit vector  aligned parallel to a principle direction (red line), and a perpendicular unit vector aligned parallel to a principle direction (red line), and a perpendicular unit vector 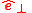 is in any radial direction relative to the principle line. is in any radial direction relative to the principle line. |
| Perpendicular to some axis/line in some radial direction | 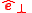 |
|
| Possible angular deviation relative to some axis/line |  |
Unit vector at acute deviation angle φ (including 0 or π/2 rad) relative to a principle direction. |
Mass and inertia
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Linear, surface, volumetric mass density | λ or μ (especially in acoustics Acoustics Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics... , see below) for Linear, σ for surface, ρ for volume. |
 (or (or 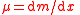 ) )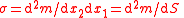 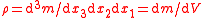 |
kg m−n, n = 1, 2, 3 | [M][L]−n |
| Moment of mass | m (No common symbol) | Point mass:  Descrete masses about an axis 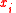 : : 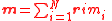 Continuum of mass about an axis 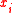 : : 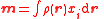 |
kg m | [M][L] |
| Centre of mass | rcom (Symbols vary) |
ith moment of mass  Discrete masses:  Mass continuum: 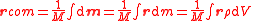 |
m | [L] |
| 2-Body reduced mass | m12, μ Pair of masses = m1 and m2 | 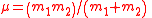 |
kg | [M][L]2 |
| Moment of inertia (MOI) | I | kg m2 s−1 | [M][L]2 | |
Derived kinematic quantities
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Velocity Velocity In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ... |
v | 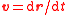 |
m s−1 | [L][T]−1 |
| Acceleration Acceleration In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ... |
a | 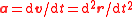 |
m s−2 | [L][T]−2 |
| Jerk | j |  |
m s−3 | [L][T]−3 |
| Angular velocity Angular velocity In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per... |
ω | 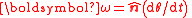 |
rad s−1 | [T]−1 |
| Angular Acceleration Angular acceleration Angular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared , and is usually denoted by the Greek letter alpha .- Mathematical definition :... |
α |  |
rad s−2 | [L][T]−2 |
Derived dynamic quantities
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Momentum Momentum In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object... |
p | 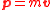 |
kg m s−1 | [M][L][T]−1 |
| Force Force In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform... |
F | 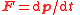 |
N = kg m s−2 | [M][L][T]−2 |
| Impulse | Δp, I |  |
kg m s−1 | [M][L][T]−1 |
| Angular momentum Angular momentum In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system... about a position point r0, |
L, J, S |  Most of the time we can set r0 = 0 if particles are orbiting about axes intersecting at a common point. |
kg m2 s−1 | [M][L]2[T]−1 |
| Moment of a force about a position point r0, Torque Torque Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist.... |
τ, M | 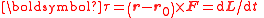 |
N m = kg m2 s−2 | [M][L]2[T]−2 |
| Angular impulse | ΔL (no common symbol) |  |
kg m2 s−1 | [M][L]2[T]−1 |
General energy definitions
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Mechanical work due to a Resultant Force |
W | 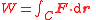 |
J = N m = kg m2 s−2 | [M][L]2[T]−2 |
| Work done ON mechanical system, Work done BY |
WON, WBY | 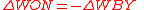 |
J = N m = kg m2 s−2 | [M][L]2[T]−2 |
| Potential energy Potential energy In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule... |
φ, Φ, U, V, Ep | 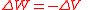 |
J = N m = kg m2 s−2 | [M][L]2[T]−2 |
| Mechanical power Power (physics) In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit... |
P | 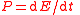 |
W = J s−1 | [M][L]2[T]−3 |
| Lagrangian Lagrangian The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as... |
L |  |
J | [M][L]2[T]−2 |
| Hamiltonian | H | 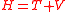 |
J | [M][L]2[T]−2 |
| Action Action (physics) In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is... |
S, 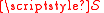 |
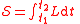 |
J s | [M][L]2[T]−1 |
Every conservative force
Conservative force
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
has a potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
. By following two principles one can consistently assign a non-relative value to U:
- Wherever the force is zero, its potential energy is defined to be zero as well.
- Whenever the force does work, potential energy is lost.
Transport mechanics
Here is a unit vector in the direction of the flow/current/flux.
is a unit vector in the direction of the flow/current/flux.| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Flow velocity Flow velocity In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid... vector field |
u |  |
m s−1 | [L][T]−1 |
| Volume velocity, volume flux | φV (no standard symbol) | 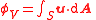 |
m3 s−1 | [L]3 [T]−1 |
| Mass current per unit volume | s (no standard symbol) | 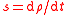 |
kg m−3 s−1 | [M] [L]−3 [T]−1 |
| Mass current, mass flow rate Mass flow rate Mass flow rate is the mass of substance which passes through a given surface per unit time. Its unit is mass divided by time, so kilogram per second in SI units, and slug per second or pound per second in US customary units... |
Im |  |
kg s−1 | [M][T]−1 |
| Mass current density | jm | 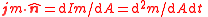 |
kg m−2 s−1 | [M][L]−2[T]−1 |
| Momentum current | Ip | kg m s−2 | [M][L][T]−2 | |
| Momentum current density | jp | kg m s−2 | [M][L][T]−2 | |
Stress and strain
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| General stress, Pressure Pressure Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :... |
P, σ | 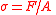 F may be any force applied to area A |
Pa = N m−2 | [M] [T] [L]−1 |
| General strain Deformation (mechanics) Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body... |
ε |  D = dimension (length, area, volume) 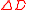 = change in dimension = change in dimension |
dimensionless | dimensionless |
| General elastic modulus Elastic modulus An elastic modulus, or modulus of elasticity, is the mathematical description of an object or substance's tendency to be deformed elastically when a force is applied to it... |
Emod | 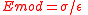 |
Pa = N m−2 | [M] [T] [L]−1 |
| Young's modulus Young's modulus Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain... |
E, Y | 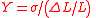 |
Pa = N m−2 | [M] [T] [L]−1 |
| Shear modulus | G |  |
Pa = N m−2 | [M] [T] [L]−1 |
| Bulk modulus Bulk modulus The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e... |
B | 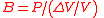 |
Pa = N m−2 | [M] [T] [L]−1 |
| Compressibility | C | 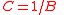 |
Pa−1 = m2 N−1 | [L] [M]−1 [T]−1 |
Thermodynamic quantities
General fundamental quantities
| Quantity (common name/s) | (Common) symbol/s | SI units | Dimension |
|---|---|---|---|
| Number of molecules | N | dimensionless | dimensionless |
| Number of moles | n | mol | [N] |
| Temperature Temperature Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot... |
T | K | [Θ] |
| Heat energy Heat In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between... |
Q, q | J | [M][L]2[T]−2 |
| Latent heat Latent heat Latent heat is the heat released or absorbed by a chemical substance or a thermodynamic system during a process that occurs without a change in temperature. A typical example is a change of state of matter, meaning a phase transition such as the melting of ice or the boiling of water. The term was... |
QL | J | [M][L]2[T]−2 |
| Entropy Entropy Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when... |
S | J K−1 | [M][L]2[T]−2 [Θ]−1 |
| Negentropy Negentropy The negentropy, also negative entropy or syntropy, of a living system is the entropy that it exports to keep its own entropy low; it lies at the intersection of entropy and life... |
J | J K−1 | [M][L]2[T]−2 [Θ]−1 |
Thermal properties of matter
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| General heat/thermal capacity | C | 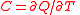 |
J K −1 | [M][L]2[T]−2 [Θ]−1 |
| Heat capacity (isobaric) | Cp | 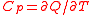 |
J K −1 | [M][L]2[T]−2 [Θ]−1 |
| Specific heat capacity (isobaric) | Cmp | 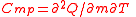 |
J kg−1 K−1 | [L]2[T]−2 [Θ]−1 |
| Molar specific heat Capacity (isobaric) |
Cnp | 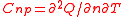 |
J K −1 mol−1 | [M][L]2[T]−2 [Θ]−1 [N]−1 |
| Heat capacity (isochoric/volumetric) | CV | 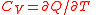 |
J K −1 | [M][L]2[T]−2 [Θ]−1 |
| Specific heat capacity (isochoric) | CmV | 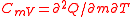 |
J kg−1 K−1 | [L]2[T]−2 [Θ]−1 |
| Molar specific heat capacity (isochoric) | CnV | 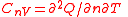 |
J K −1 mol−1 | [M][L]2[T]−2 [Θ]−1 [N]−1 |
| Specific latent heat | L | 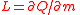 |
J kg−1 | [L]2[T]−2 |
| Ratio of isobaric to isochoric heat capacity, Heat capacity ratio Heat capacity ratio The heat capacity ratio or adiabatic index or ratio of specific heats, is the ratio of the heat capacity at constant pressure to heat capacity at constant volume . It is sometimes also known as the isentropic expansion factor and is denoted by \gamma or \kappa . The latter symbol kappa is... , adiabatic index |
γ | 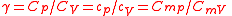 |
dimensionless | dimensionless |
Thermal transfer
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Temperature gradient Temperature gradient A temperature gradient is a physical quantity that describes in which direction and at what rate the temperature changes the most rapidly around a particular location. The temperature gradient is a dimensional quantity expressed in units of degrees per unit length... |
No standard symbol | 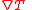 |
K m−1 | [Θ][L]−1 |
| Thermal conduction rate, thermal current, thermal/heat flux Heat flux Heat flux or thermal flux is the rate of heat energy transfer through a given surface. The SI derived unit of heat rate is joule per second, or watt. Heat flux is the heat rate per unit area. In SI units, heat flux is measured in W/m2]. Heat rate is a scalar quantity, while heat flux is a vectorial... , thermal power transfer |
P | 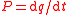 |
W = J s−1 | [M] [L]2 [T]−2 |
| Thermal intensity | I |  |
W m−2 | [M] [T]−3 |
| Thermal/heat flux density (vector analogue of thermal intensity above) | q | 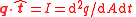 |
W m−2 | [M] [T]−3 |
General fundamental quantities
A wave can be longnitudinalLongitudinal wave
Longitudinal waves, as known as "l-waves", are waves that have the same direction of vibration as their direction of travel, which means that the movement of the medium is in the same direction as or the opposite direction to the motion of the wave. Mechanical longitudinal waves have been also...
where the oscillations are parallel (or antiparallel) to the propagation direction, or transverse
Transverse wave
A transverse wave is a moving wave that consists of oscillations occurring perpendicular to the direction of energy transfer...
where the oscillations are perpendicular to the propagation direction. These oscillations are characterized by a periodically time-varying displacement in the parallel or perpendicular direction, and so the instantaneous velocity and acceleration are also periodic and time varying in these directions. But the wave profile (the apparent motion of the wave due to the successive oscillations of particles or fields about their equilibrium positions) propagates at the phase and group velocities parallel or antiparallel to the propagation direction, which is common to longitudinal and transverse waves. Below oscillatory displacement, velocity and acceleration refer to the kinematics in the oscillating directions of the wave - transverse or longitudinal (mathematical description is identical), the group and phase velocities are separate.
| Quantity (common name/s) | (Common) symbol/s | SI units | Dimension |
|---|---|---|---|
| Number of wave cycles | N | dimensionless | dimensionless |
| (Oscillatory) displacement | Symbol of any quantity which varies periodically, such as h, x, y (mechanical waves), x, s, η (longitudinal waves) I, V, E, B, H, D (electromagnetism), u, U (luminal waves), ψ, Ψ, Φ (quantum mechanics). Most general purposes use y, ψ, Ψ. For generality here, A is used and can be replaced by any other symbol, since others have specific, common uses.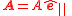 for longitudinal waves, for longitudinal waves, for transverse waves. for transverse waves. |
m | [L] |
| (Oscillatory) displacement amplitude Amplitude Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation... |
Any quantity symbol typically subscripted with 0, m or max, or the capitalized letter (if displacement was in lower case). Here for generality A0 is used and can be replaced. | m | [L] |
| (Oscillatory) velocity amplitude | V, v0, vm. Here v0 is used. | m s−1 | [L][T]−1 |
| (Oscillatory) acceleration amplitude | A, a0, am. Here a0 is used. | m s−2 | [L][T]−2 |
| Spatial position Position of a point in space, not necessarily a point on the wave profile or any line of propagation |
d, r | m | [M] |
| Wave profile displacement Along propagation direction, distance travelled (path length) by one wave from the source point r0 to any point in space d (for longitudinal or transverse waves) |
L, d, r |
m | [L] |
| Phase angle Phase angle In the context of vectors and phasors, the term phase angle refers to the angular component of the polar coordinate representation. The notation A\ang \!\ \theta, for a vector with magnitude A and phase angle θ, is called angle notation.In the context of periodic phenomena, such as a wave,... |
δ, ε, φ | rad | dimensionless |
General derived quantities
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Wavelength Wavelength In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a... |
λ | General definition (allows for FM Frequency modulation In telecommunications and signal processing, frequency modulation conveys information over a carrier wave by varying its instantaneous frequency. This contrasts with amplitude modulation, in which the amplitude of the carrier is varied while its frequency remains constant... ): 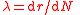 For non-FM waves this reduces to:  |
m | [L] |
| Wavenumber, k-vector, Wave vector Wave vector In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In... |
k, σ | Two definitions are in use:  |
m−1 | [L]−1 |
| Frequency Frequency Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency... |
f, ν | General definition (allows for FM Frequency modulation In telecommunications and signal processing, frequency modulation conveys information over a carrier wave by varying its instantaneous frequency. This contrasts with amplitude modulation, in which the amplitude of the carrier is varied while its frequency remains constant... ): 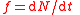 For non-FM waves this reduces to: 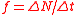 In practice N is set to 1 cycle and t = T = time period for 1 cycle, to obtain the more useful relation: 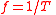 |
Hz = s−1 | [T]−1 |
| Angular frequency Angular frequency In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity... / pulsatance |
ω | 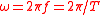 |
Hz = s−1 | [T]−1 |
| Oscillatory velocity | v, vt, v | Longitudinal waves: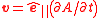 Transverse waves:  |
m s−1 | [L][T]−1 |
| Oscillatory acceleration | a, at | Longitudinal waves: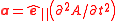 Transverse waves: 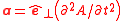 |
m s−2 | [L][T]−2 |
| Path length difference between two waves | L, ΔL, Δx, Δr | 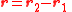 |
m | [L] |
| Phase velocity Phase velocity The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity... |
vp | General definition: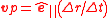 In practice reduces to the useful form:  |
m s−1 | [L][T]−1 |
| (Longitudinal) group velocity Group velocity The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space.... |
vg | 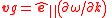 |
m s−1 | [L][T]−1 |
| Time delay, time lag/lead | Δt |  |
s | [T] |
| Phase difference | δ, Δε, Δϕ | 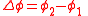 |
rad | dimensionless |
| Phase Phase (waves) Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:... |
No standard symbol |  Physically; upper sign: wave propagation in +r direction lower sign: wave propagation in −r direction Phase angle can lag if: ϕ > 0 or lead if: ϕ < 0. |
rad | dimensionless |
Relation between space, time, angle analogues used to describe the phase:
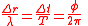
Modulation indicies
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| AM index: |
h, hAM | 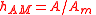 A = carrier amplitude Am = peak amplitude of a component in the modulating signal |
dimensionless | dimensionless |
| FM index: |
hFM | 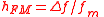 Δf = max. deviation of the instantaneous frequency from the carrier frequency fm = peak frequency of a component in the modulating signal |
dimensionless | dimensionless |
| PM index: |
hPM |  Δϕ = peak phase deviation |
dimensionless | dimensionless |
Acoustics
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Acoustic impedance | Z |  v = speed of sound, ρ = volume density of medium |
kg m−2 s−1 | [M] [L]−2 [T]−1 |
| Specific acoustic impedance | z |  S = surface area |
kg s−1 | [M] [T]−1 |
| Sound Level Sound pressure Sound pressure or acoustic pressure is the local pressure deviation from the ambient atmospheric pressure caused by a sound wave. Sound pressure can be measured using a microphone in air and a hydrophone in water... |
β | dimensionless | dimensionless | |
Gravitation
A common misconseption occurs between centre of mass and centre of gravityCenter of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
. They are defined in similar ways but are not exactly the same quantity. Centre of mass is the mathematical descrition of placing all the mass in the region considered to one position, centre of gravity is a real physical quantity, the point of a body where the gravitational force acts. They are only equal if and only if the external gravitational field is uniform.
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Centre of gravity | rcog (symbols vary) |
& = \frac{1}{M \left | \mathbf{g} \left ( \mathbf{r}_\mathrm{cog} \right ) \right |}\sum_i \mathbf{r}_i m_i \left | \mathbf{g} \left ( \mathbf{r}_i \right ) \right | \end{align}\,\!
Centre of a gravity for a continuum of mass:
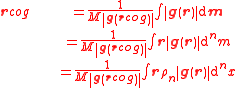
| m
| [L]
|-
|Standard gravitational parameter
Standard gravitational parameter
In astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
of a mass
| μ
|

| N m2 kg−1
| [L]3 [T]−2
|-
|Gravitational field
Gauss' law for gravity
In physics, Gauss's law for gravity, also known as Gauss's flux theorem for gravity, is a law of physics which is essentially equivalent to Newton's law of universal gravitation...
, field strength, potential gradient, acceleration
| g
|
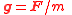
| N kg−1 = m s−2
| [L][T]−2
|-
|Gravitational flux
Gauss' law for gravity
In physics, Gauss's law for gravity, also known as Gauss's flux theorem for gravity, is a law of physics which is essentially equivalent to Newton's law of universal gravitation...
| ΦG
|
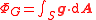
| m3 s−2
| [L]3[T]−2
|-
|Absolute gravitational potential
| Φ, φ, U, V
|
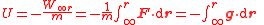
| J kg−1
| [L]2[T]−2
|-
|Gravitational potential difference
| ΔΦ, Δφ, ΔU, ΔV
|

| J kg−1
| [L]2[T]−2
|-
|Gravitational potential energy
Gravitational energy
Gravitational energy is the energy associated with the gravitational field. This phrase is found frequently in scientific writings about quasars and other active galaxies.-Newtonian mechanics:...
|| Ep
|

| J
| [M][L]2[T]−2
|-
|Gravitational torsion field|| Ω
|

| Hz = s−1
| [T]−1
|-
|Gravitational torsion flux|| ΦΩ
|
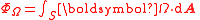
| N m s kg−1 = m2 s−1
| [M]2 [T]−1
|-
|Gravitomagnetic field
Gravitomagnetism
Gravitomagnetism , refers to a set of formal analogies between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. The most common version of GEM is valid only far from isolated sources, and for slowly moving test...
|| H, Bg, B, ξ
|

| Hz = s−1
| [T]−1
|-
|Gravitomagnetic flux
| Φξ
|
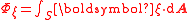
| N m s kg−1 = m2 s−1
| [M]2 [T]−1
|-
|Gravitomagnetic vector potential
| h
|

| m s−1
| [M] [T]−1
|-
|}
Electromagnetism
Here subscripts e and m are used to differ between electric and magnetic charges. The definitions for monopoles are of theoretical interest, although real magnetic dipoles can be described using pole strengths. There are two possible units for monopole strength, Wb (Weber) and A m (Ampere metre). Dimensional analysis shows that magnetic charges relate by qm(Wb) = μ0 qm(Am).Initial quantities
| Quantity (common name/s) | (Common) symbol/s | SI units | Dimension |
|---|---|---|---|
| Electric charge Electric charge Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two... |
qe, q, Q | C = As | [I][T] |
| Monopole strength, magnetic charge | qm, g, p | Wb or Am | [L]2[M][T]−2 [I]−1 (Wb) [I][L] (Am) |
Electric quantities
Contrary to the strong analogy between (classical) gravitationGravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
and electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, there are no "centre of charge" or "centre of electrostatic attraction" analogues.
Electric transport
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Linear, surface, volumetric charge density | λe for Linear, σe for surface, ρe for volume. | 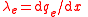 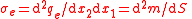 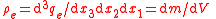 |
C m−n, n = 1, 2, 3 | [I][T][L]−n |
| Capacitance Capacitance In electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor... |
C |  V = voltage, not volume. |
F = C V−1 | [I][T]3[L]−2[M]−1 |
| Electric current Electric current Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire... |
I | 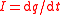 |
A | [I] |
| Electric current density | J |  |
A m−2 | [I][L]−2 |
| Displacement current Displacement current In electromagnetism, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do. However it is not an electric... density |
Jd | 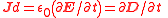 |
Am−2 | [I][L]m−2 |
| Convection current density | Jc |  |
A m−2 | [I] [L]m−2 |
Electric fields
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... , field strength, flux density, potential gradient |
E | 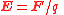 |
N C−1 = V m−1 | [M][L][T]−3[I]−1 |
| Electric flux | ΦE | 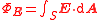 |
N m2 C−1 | [M][L]3[T]−3[I]−1 |
| Absolute permittivity Permittivity In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how... ; |
ε | 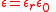 |
F m−1 | [I]2 [T]4 [M]−1 [L]−3 |
| Electric displacement field | D | 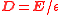 |
C m−2 | [I][T][L]−2 |
| Electric displacement flux | ΦD | 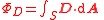 |
C | [I][T] |
| Electric dipole moment Electric dipole moment In physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter... |
p | 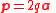 a = charge separation directed from -ve to +ve charge |
C m | [I][T][L] |
| Electric Polarization, polarization density Polarization density In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is... |
P |  |
C m−2 | [I][T][L]−2 |
| Absolute electric potential Electric potential In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there... , EM scalar potential relative to point  Theoretical:  Practical:  (Earth's radius) (Earth's radius) |
φ ,V | 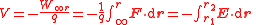 |
V = J C−1 | [M] [L] [T]−3 [I]−1 |
| Voltage Voltage Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points... , Electric potential difference |
Δφ,ΔV |  |
V = J C−1 | [M] [L] [T]−3 [I]−1 |
| Electric potential energy Electric potential energy Electric potential energy, or electrostatic potential energy, is a potential energy that results from conservative Coulomb forces and is associated with the configuration of a particular set of point charges within a defined system... |
U |  |
J | [M][L]2[T]2 |
Magnetic quantities
Magnetic transport| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Linear, surface, volumetric pole density | λm for Linear, σm for surface, ρm for volume. | 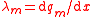 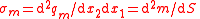  |
Wb m−n A m−(n + 1), n = 1, 2, 3 |
[L]2[M][T]−2 [I]−1 (Wb) [I][L] (Am) |
| Monopole current | Im | 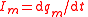 |
Wb s−1 A m s−1 |
[L]2[M][T]−3 [I]−1 (Wb) [I][L][T]−1 (Am) |
| Monopole current density | Jm |  |
Wb s−1 m−2 A m−1 s−1 |
[M][T]−3 [I]−1 (Wb) [I][L]−1[T]−1 (Am) |
Magnetic fields
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Magnetic field Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... , field strength, flux density, induction field |
B | 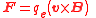 |
T = N A−1 m−1 = Wb m2 | [M][T]−2[I]−1 |
| Magnetic potential Magnetic potential The term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ... , EM vector potential |
A |  |
T m = N A−1 = Wb m3 | [M][L][T]−2[I]−1 |
| Magnetic flux | ΦB |  |
Wb = T m−2 | [L]2[M][T]−2[I]−1 |
| Magnetic field Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... intensity, (AKA field strength) |
H | 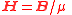 |
A m−1 | [I] [L]−1 |
| Magnetic moment Magnetic moment The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it... , magnetic dipole moment |
m, μ, Π | Two definitions are possible: using pole strengths, 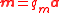 using currents:  a = pole separation N is the number of turns of conductor |
A m2 | [I][L]2 |
| Magnetization Magnetization In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material... |
M | 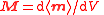 |
A m2 | [I] [L]−1 |
| Intensity of magnetization Magnetic susceptibility In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field... , magnetic polarization |
I, J | 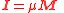 |
T = N A−1 m−1 = Wb m2 | [M][T]−2[I]−1 |
| Self Inductance Inductance In electromagnetism and electronics, inductance is the ability of an inductor to store energy in a magnetic field. Inductors generate an opposing voltage proportional to the rate of change in current in a circuit... |
L | Two equivalent definitions are possible: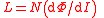 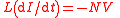 |
H = Wb A−1 | [L]2 [M] [T]−2 [I]−2 |
| Mutual inductance Inductance In electromagnetism and electronics, inductance is the ability of an inductor to store energy in a magnetic field. Inductors generate an opposing voltage proportional to the rate of change in current in a circuit... |
M | Again two equivalent definitions are possible: 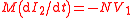 1,2 subscripts refer to two conductors/inductors mutually inducing voltage/ linking magnetic flux though each other. They can be interchanged for the required conductor/inductor; 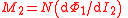 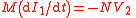 |
H = Wb A−1 | [L]2 [M] [T]−2 [I]−2 |
| Gyromagnetic ratio (for charged particles in a magnetic field) | γ | 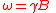 |
Hz T−1 | [M]−1[T][I] |
Electric circuits
DC circuits, general definitions| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Terminal Voltage for Power Supply Power supply A power supply is a device that supplies electrical energy to one or more electric loads. The term is most commonly applied to devices that convert one form of electrical energy to another, though it may also refer to devices that convert another form of energy to electrical energy... |
Vter | V = J C−1 | [M] [L]2 [T]−3 [I]−1 | |
| Load Voltage for Circuit | Vload | V = J C−1 | [M] [L]2 [T]−3 [I]−1 | |
| Internal resistance of power supply | Rint |  |
Ω = V A−1 = J s C−2 | [M][L]2 [T]−3 [I]−2 |
| Load resistance of circuit | Rext | 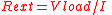 |
Ω = V A−1 = J s C−2 | [M][L]2 [T]−3 [I]−2 |
| Electromotive force Electromotive force In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a... (emf), voltage across entire circuit including power supply, external components and conductors |
E |  |
V = J C−1 | [M] [L]2 [T]−3 [I]−1 |
AC circuits
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Resistive load voltage | VR | 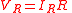 |
V = J C−1 | [M] [L]2 [T]−3 [I]−1 |
| Capacitive load coltage | VC | 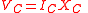 |
V = J C−1 | [M] [L]2 [T]−3 [I]−1 |
| Inductive load coltage | VL | 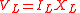 |
V = J C−1 | [M] [L]2 [T]−3 [I]−1 |
| Capacitive reactance | XC |  |
Ω−1 m−1 | [I]2 [T]3 [M]−2 [L]−2 |
| Inductive reactance | XL | 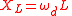 |
Ω−1 m−1 | [I]2 [T]3 [M]−2 [L]−2 |
| AC electrical impedance Impedance Impedance may refer to:*Electrical impedance, the ratio of the voltage phasor to the electric current phasor, a measure of the opposition to time-varying electric current in an electric circuit**Characteristic impedance of a transmission line... |
Z |  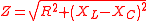 |
Ω−1 m−1 | [I]2 [T]3 [M]−2 [L]−2 |
| Phase constant | δ, φ | 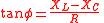 |
dimensionless | dimensionless |
| AC peak current | I0 | 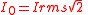 |
A | [I] |
| AC root mean square current | Irms | 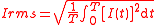 |
A | [I] |
| AC peak voltage | V0 | 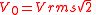 |
V = J C−1 | [M] [L]2 [T]−3 [I]−1 |
| AC root mean square voltage | Vrms |  |
V = J C−1 | [M] [L]2 [T]−3 [I]−1 |
| AC emf, root mean square |  |
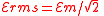 |
V = J C−1 | [M] [L]2 [T]−3 [I]−1 |
| AC average power | 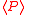 |
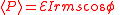 |
W = J s−1 | [M] [L]2 [T]−3 |
| Capacitive time constant | τC |  |
s | [T] |
| Inductive time constant | τL | 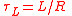 |
s | [T] |
Magnetic circuits
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Magnetomotive force Magnetomotive force Magnetomotive force is any physical driving force that produces magnetic flux. In this context, the expression "driving force" is used in a general sense of "work potential", and is analogous, but distinct from force measured in newtons... , mmf |
F,  |
 N = number of turns of conductor |
A | [I] |
General fundamental quantities
| Quantity (common name/s) | (Common) symbol/s | SI units | Dimension |
|---|---|---|---|
| Object distance | x, s, d, u, x1, s1, d1, u1 | m | [L] |
| Image distance | x', s', d', v, x2, s2, d2, v2 | m | [L] |
| Object height | y, h, y1, h1 | m | [L] |
| Image height | y', h', H, y2, h2, H2 | m | [L] |
| Angle subtended by object | θ, θo, θ1 | rad | dimensionless |
| Angle subtended by image | θ', θi, θ2 | rad | dimensionless |
| Curvature radius of lens/mirror | r, R | m | [L] |
| Focal length | f | m | [L] |
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Lens power | P | 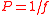 |
m−1 = D (dioptre) | [L]−1 |
| Lateral magnification | m | 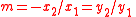 |
dimensionless | dimensionless |
| Angular magnification | m | 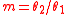 |
dimensionless | dimensionless |
Physical optics (EM luminal waves)
There are different forms of the Poynting vectorPoynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
, the most common are in terms of the E and B or E and H fields.
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Poynting vector Poynting vector In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector... |
S, N |  |
W m−2 | [M][T]−3 |
| Poynting flux, EM field power flow | ΦS, ΦN | 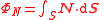 |
W | [M][L]2[T]−3 |
| RMS Root mean square In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids... Electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... of Light |
Erms | 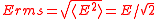 |
N C−1 = V m−1 | [M][L][T]−3[I]−1 |
| Radiation momentum | p, pEM, pr | 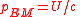 |
J s m−1 | [M][L][T]−1 |
| Radiation pressure Radiation pressure Radiation pressure is the pressure exerted upon any surface exposed to electromagnetic radiation. If absorbed, the pressure is the power flux density divided by the speed of light... |
Pr, pr, PEM | 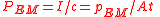 |
W m−2 | [M][T]−3 |
Radiometry
For spectral quantities two definitions are in use to refer to the same quantity, in terms of frequency or wavelength.| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Radiant energy Radiant energy Radiant energy is the energy of electromagnetic waves. The quantity of radiant energy may be calculated by integrating radiant flux with respect to time and, like all forms of energy, its SI unit is the joule. The term is used particularly when radiation is emitted by a source into the... |
Q, E, Qe, Ee | J | [M][L]2[T]−2 | |
| Radiant exposure | He |  |
J m−2 | [M][T]−3 |
| Radiant energy density | ωe | 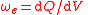 |
J m−3 | [M][L]−3 |
| Radiant flux Radiant flux In radiometry, radiant flux or radiant power is the measure of the total power of electromagnetic radiation... , radiant power |
Φ, Φe | 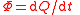 |
W | [M][L]2[T]−3 |
| Radiant intensity Radiant intensity In radiometry, radiant intensity is a measure of the intensity of electromagnetic radiation. It is defined as power per unit solid angle. The SI unit of radiant intensity is watts per steradian . Radiant intensity is distinct from irradiance and radiant exitance, which are often called intensity... |
I, Ie | 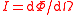 |
W sr−1 | [M][L]2[T]−3 |
| Radiance Radiance Radiance and spectral radiance are radiometric measures that describe the amount of radiation such as light or radiant heat that passes through or is emitted from a particular area, and falls within a given solid angle in a specified direction. They are used to characterize both emission from... , intensity |
L, Le | 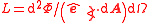 |
W sr−1 m−2 | [M][T]−3 |
| Irradiance Irradiance Irradiance is the power of electromagnetic radiation per unit area incident on a surface. Radiant emittance or radiant exitance is the power per unit area radiated by a surface. The SI units for all of these quantities are watts per square meter , while the cgs units are ergs per square centimeter... |
E, I, Ee, Ie | 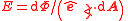 |
W m−2 | [M][T]−3 |
| Radiant exitance, radiant emittance | M, Me | 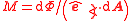 |
W m−2 | [M][T]−3 |
| Radiosity Radiosity (heat transfer) Radiosity is a convenient quantity in optics and heat transfer that represents the total radiation intensity leaving a surface. Radiosity accounts for two components: the radiation being emitted by the surface, and the radiation being reflected from the surface... |
J, Jν, Je, Jeν | 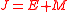 |
W m−2 | [M][T]−3 |
| Spectral radiant flux, spectral radiant power | Φλ, Φν, Φeλ, Φeν | 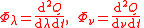 |
W m−1 (Φλ) W Hz−1 = J (Φν) |
[M][L]−3[T]−3 (Φλ) [M][L]−2[T]−2 (Φν) |
| Spectral radiant intensity | Iλ, Iν, Ieλ, Ieν | 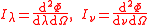 |
W sr−1 m−1 (Iλ) W sr−1 Hz−1 (Iν) |
[M][L]−3[T]−3 (Iλ) [M][L]2[T]−2 (Iν) |
| Spectral radiance | Lλ, Lν, Leλ, Leν | 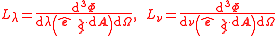 |
W sr−1 m−3 (Lλ) W sr−1 m−2 Hz−1 (Lν) |
[M][L]−1[T]−3 (Lλ) [M][L]−2[T]−2 (Lν) |
| Spectral irradiance | Eλ, Eν, Eeλ, Eeν |  |
W m−3 (Eλ) W m−2 Hz−1 (Eν) |
[M][L]−1[T]−3 (Eλ) [M][L]−2[T]−2 (Eν) |
Atomic/nuclear physics
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Number of atoms | N = Number of atoms remaining at time t N0 = Initial number of atoms at time t = 0 ND = Number of atoms decayed at time t |
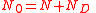 |
dimensionless | dimensionless |
| Decay rate, activity of a radioisotope | A | 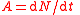 |
Bq = Hz = s−1 | [T]−1 |
| Decay constant | λ | 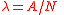 |
Bq = Hz = s−1 | [T]−1 |
| Half-life Half-life Half-life, abbreviated t½, is the period of time it takes for the amount of a substance undergoing decay to decrease by half. The name was originally used to describe a characteristic of unstable atoms , but it may apply to any quantity which follows a set-rate decay.The original term, dating to... of a radioisotope |
t1/2, T1/2 | Time taken for half the number of atoms present to decay 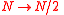 |
s | [T] |
| Number of half-lives | n (no standard symbol) | 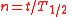 |
dimensionless | dimensionless |
| Radioisotope time constant, mean lifetime of an atom before decay | τ (no standard symbol) | 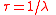 |
s | [T] |
| Absorbed dose, total ionizing dose (total energy of radiation transferred to unit mass) | D can only be found experimentally | N/A | Sv = J kg−1 (Sievert) | [L]2[T]−2 |
| Equivalent dose Equivalent dose The equivalent absorbed radiation dose, usually shortened to equivalent dose, is a computed average measure of the radiation absorbed by a fixed mass of biological tissue, that attempts to account for the different biological damage potential of different types of ionizing radiation... |
H | 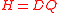 Q = radiation quality factor (dimensionless) |
Sv = J kg−1 (Sievert) | [L]2[T]−2 |
| Effective dose Effective dose Effective dose may refer to:*Effective dose the dose of pharmacologic agent which will have a therapeutic effect in some fraction of the population receiving the drug... |
E |  Wj = weighting factors corresponding to radiosensitivities of matter (dimensionless)  |
Sv = J kg−1 (Sievert) | [L]2[T]−2 |
Quantum mechanics
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Wave function | ψ, Ψ | To solve from the Schrödinger equation Schrödinger equation The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time.... |
varies with situation and number of particles | |
| Threshold frequency Photoelectric effect In the photoelectric effect, electrons are emitted from matter as a consequence of their absorption of energy from electromagnetic radiation of very short wavelength, such as visible or ultraviolet light. Electrons emitted in this manner may be referred to as photoelectrons... |
f0, ν0 | Can only be found by experiment/calculated from work function below. | Hz = s−1 | [T]−1 |
| Work function Work function In solid-state physics, the work function is the minimum energy needed to remove an electron from a solid to a point immediately outside the solid surface... |
φ, Φ | 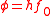 |
J | [M][L]2[T]−2 |
| Wavefunction probability density Probability density Probability density may refer to:* Probability density function in probability theory* The product of the probability amplitude with its complex conjugate in quantum mechanics... |
ρ | m−3 | [L]−3 | |
| Wavefunction probability current Probability current In quantum mechanics, the probability current is a mathematical quantity describing the flow of probability density. Intuitively; if one pictures the probability density as an inhomogeneous fluid, then the probability current is the rate of flow of this fluid... |
j | Non-relativistic, no external field: 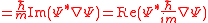 star * is complex conjugate Complex conjugate In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs... |
m−2 s−1 | [T]−1 [L]−2 |
Astrophysics
In astrophysics, L is used for luminosity (energy per unit time, equivalent to power) and F is used for energy flux (energy per unit time per unit area, equivalent to intensity in terms of area, not solid angle). They are not new quantities, simply different names.| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Comoving transverse distance | DM | pc (parsecs) | [L] | |
| Luminosity distance | DL | 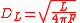 |
pc (parsecs) | [L] |
| Apparent magnitude Apparent magnitude The apparent magnitude of a celestial body is a measure of its brightness as seen by an observer on Earth, adjusted to the value it would have in the absence of the atmosphere... in band j (UV, visible and IR parts of EM spectrum) (Bolometric) |
m | dimensionless | dimensionless | |
| Absolute magnitude Absolute magnitude Absolute magnitude is the measure of a celestial object's intrinsic brightness. it is also the apparent magnitude a star would have if it were 32.6 light years away from Earth... (Bolometric) |
M | 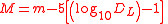 |
dimensionless | dimensionless |
| Distance modulus Distance modulus -Definition:The distance modulus \mu=m-M is the difference between the apparent magnitude m and the absolute magnitude M of an astronomical object... |
μ |  |
dimensionless | dimensionless |
| Colour indices Color index In astronomy, the color index is a simple numerical expression that determines the color of an object, which in the case of a star gives its temperature... |
(No standard symbols) | 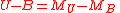  |
dimensionless | dimensionless |
| Bolometric correction Bolometric Correction In astronomy, a bolometric correction is a correction that must be made to the absolute magnitude of an object in order to convert an object's visible magnitude to its bolometric magnitude. Mathematically, such a calculation can be expressed: BC = M_b - M_v\!\,... |
Cbol (No standard symbol) | 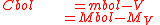 |
dimensionless | dimensionless |