
List of numbers
Encyclopedia
This is a list of articles about number
s (not about numerals
).
Natural number
Prime number
A prime number is a positive integer which has exactly two divisor
s: one and itself.
The first 100 prime numbers:
| 2 >
3
5
7
11
13
17
19
23
29
>-
| 31
37
41
43
47
53
59
61
67
71
>-
| 73
79
83
89
97
101
103
107
109
113
>-
|127
131
137
139
149
151
157
163
167
173
>-
|179
181
191
193
197
199
211
223
227
229
>-
|233
239
241
251
257
263
269
271
277
|283293
307
311
313
317
331
337
347
|353
359
367
373
379
383
389
397
401
|419
421
431
433
439
443
449
457
461
|467479
487
491
499
503
509
521
523
Perfect number
A perfect number is an integer that is the sum of its positive proper divisors (all divisors except itself).
The first 10 perfect numbers:
Cardinal number
In the following tables, [and] indicates that the word and is used in some dialect
s (such as British English
), and omitted in other dialects (such as American English
).
for more information on naming numbers.
There is no consistent and widely accepted way to extend cardinals beyond centillion
(centilliard).
Proposed by Donald E. Knuth:
Fractional
This is a table of English names for positive rational number
s less than or equal to 1. It also lists alternative names, but there is no widespread convention for the names of extremely small positive numbers.
Keep in mind that rational numbers like 0.12 can be represented in infinitely many ways, e.g. zero-point-one-two (0.12), twelve percent (12%), three twenty-fifths , nine seventy-fifths
, nine seventy-fifths  , six fiftieths
, six fiftieths  , twelve hundredths
, twelve hundredths  , twenty-four two-hundredths
, twenty-four two-hundredths  , etc.
, etc.
Algebraic number
Transcendental number
Algebraic complex number
Transfinite number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s (not about numerals
Number names
In linguistics, number names are specific words in a natural language that represent numbers.In writing, numerals are symbols also representing numbers...
).
Natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s
| 0 0 (number) 0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems... |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 10 (number) 10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and... |
11 11 (number) 11 is the natural number following 10 and preceding 12.Eleven is the first number which cannot be counted with a human's eight fingers and two thumbs additively. In English, it is the smallest positive integer requiring three syllables and the largest prime number with a single-morpheme name... |
12 12 (number) 12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten... |
13 13 (number) 13 is the natural number after 12 and before 14. It is the smallest number with eight letters in its name spelled out in English. It is also the first of the teens – the numbers 13 through 19 – the ages of teenagers.... |
14 14 (number) 14 is the natural number following 13 and preceding 15.In speech, the numbers 14 and 40 are often confused. When carefully enunciated, they differ in which syllable is stressed: 14 vs 40... |
15 15 (number) 15 is the natural number following 14 and preceding 16. In English, it is the smallest natural number with seven letters in its spelled name.... |
16 16 (number) 16 is the natural number following 15 and preceding 17. 16 is a composite number, and a square number, being 42 = 4 × 4. It is the smallest number with exactly five divisors, its proper divisors being , , and .... |
17 17 (number) 17 is the natural number following 16 and preceding 18. It is prime.In spoken English, the numbers 17 and 70 are sometimes confused because they sound similar. When carefully enunciated, they differ in which syllable is stressed: 17 vs 70... |
18 18 (number) 18 is the natural number following 17 and preceding 19.In speech, the numbers 18 and 80 are sometimes confused. When carefully enunciated, they differ in which syllable is stressed: 18 vs 80 . However, in dates such as 1864, or when contrasting numbers in the teens, such as 17, 18, 19, the stress... |
19 19 (number) 19 is the natural number following 18 and preceding 20. It is a prime number.In English speech, the numbers 19 and 90 are often confused. When carefully enunciated, they differ in which syllable is stressed: 19 vs 90... |
| 20 20 (number) 20 is the natural number following 19 and preceding 21. A group of twenty units may also be referred to as a score.-In mathematics:*20 is the basis for vigesimal number systems.... |
21 21 (number) 21 is the natural number following 20 and preceding 22.-In mathematics:Twenty-one is the fifth discrete Semiprime and the second in the family. With 22 it forms the second discrete Semiprime pair... |
22 22 (number) 22 is the natural number following 21 and preceding 23.- In mathematics :Twenty-two is an even composite number, its proper divisors being 1, 2 and 11.... |
23 23 (number) 23 is the natural number following 22 and preceding 24.- In mathematics :Twenty-three is the ninth prime number, the smallest odd prime that is not a twin prime. Twenty-three is also the fifth factorial prime, the third Woodall prime... |
24 24 (number) 24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto... |
25 25 (number) 25 is the natural number following 24 and preceding 26.-In mathematics:It is a square number, being 5² = 5 × 5. It is the smallest square that is also a sum of two squares: 25 = 3² + 4²... |
26 26 (number) 26 is the natural number following 25 and preceding 27.- In mathematics :26 is the only positive integer that is one greater than a square and one less than a cube .A rhombicuboctahedron has twenty-six sides.... |
27 27 (number) 27 is the natural number following 26 and preceding 28.- In mathematics :Twenty-seven is a perfect cube, being 33 = 3 × 3 × 3. 27 is also 23 . There are exactly 27 straight lines on a smooth cubic surface, which give a basis of the fundamental representation of the E6 Lie algebra... |
28 28 (number) 28 is the natural number following 27 and preceding 29.-In mathematics:It is a composite number, its proper divisors being 1, 2, 4, 7, and 14.... |
29 29 (number) 29 is the natural number following 28 and preceding 30.-In mathematics:It is the tenth prime number, and also the fourth primorial prime. It forms a twin prime pair with thirty-one, which is also a primorial prime. Twenty-nine is also the sixth Sophie Germain prime. It is also the sum of three... |
| 30 30 (number) 30 is the natural number following 29 and preceding 31.-In mathematics:30 is the sum of the first four squares, which makes it a square pyramidal number.It is a primorial and is the smallest Giuga number.... |
31 31 (number) 31 is the natural number following 30 and preceding 32.- In mathematics :Thirty-one is the third Mersenne prime as well as the fourth primorial prime, and together with twenty-nine, another primorial prime, it comprises a twin prime. As a Mersenne prime, 31 is related to the perfect number 496,... |
32 32 (number) 32 is the natural number following 31 and preceding 33.-In mathematics:32 is the smallest number n with exactly 7 solutions to the equation φ = n... |
33 33 (number) 33 is the natural number following 32 and preceding 34.-In mathematics:33 is the largest positive integer that cannot be expressed as a sum of different triangular numbers. It is also the smallest odd repdigit that is not a prime number.33 is the eighth distinct semiprime comprising the prime... |
34 34 (number) 34 is the natural number following 33 and preceding 35.-In mathematics:34 is the ninth distinct semiprime and has four divisors including unity and itself. Its neighbors, 33 and 35, also are distinct semiprimes, having four divisors each, and 34 is the smallest number to be surrounded by numbers... |
35 35 (number) 35 is the natural number following 34 and preceding 36.- In mathematics :35 is the sum of the first five triangular numbers, making it a tetrahedral number.... |
36 36 (number) 36 is the natural number following 35 and preceding 37.- In mathematics :36 is both the square of 6 and a triangular number, making it a square triangular number... |
37 37 (number) 37 is the natural number following 36 and preceding 38.-In mathematics:It is a prime number, the fifth lucky prime, the first irregular prime, the third unique prime and the third cuban prime of the form... |
38 38 (number) This article discusses the number thirty-eight. For the year 38 CE, see 38. For other uses of 38, see 38 38 is the natural number following 37 and preceding 39.-In mathematics:... |
39 39 (number) 39 is the natural number following 38 and preceding 40.- In mathematics :Thirty-nine is the sum of five consecutive primes and the sum of the first three powers of 3... |
| 40 40 (number) 40 is the natural number following 39 and preceding 41.Despite being related to the word "four" , 40 is spelled "forty", and not "fourty"... |
41 41 (number) 41 is the natural number following 40 and preceding 42.-In mathematics:Forty-one is the 13th smallest prime number. The next is forty-three, with which it comprises a twin prime... |
42 42 (number) 42 is the natural number immediately following 41 and directly preceding 43. The number has received considerable attention in popular culture as a result of its central appearance in The Hitchhiker's Guide to the Galaxy as the "Answer to the Ultimate Question of Life, the Universe, and... |
43 43 (number) 43 is the natural number following 42 and preceding 44.- In mathematics :Forty-three is the 14th smallest prime number. The previous is forty-one, with which it comprises a twin prime, and the next is forty-seven. 43 is the smallest prime that is not a Chen prime... |
44 44 (number) 44 is the natural number following 43 and preceding 45.- In mathematics :Forty-four is a tribonacci number, a happy number, an octahedral number and a palindromic number.... |
45 45 (number) 45 is the natural number following 44 and followed by 46.- In mathematics :Forty-five is a triangular number, a hexagonal and 16-gonal number, a Kaprekar number, and a Harshad number.... |
46 46 (number) 46 is the natural number following 45 and preceding 47.- In mathematics :Forty-six is a Wedderburn-Etherington number, an enneagonal number and a centered triangular number. It is the sum of the totient function for the first twelve integers. 46 is the largest even integer that can't be expressed... |
47 47 (number) 47 is the natural number following 46 and preceding 48.-In mathematics:Forty-seven is the fifteenth prime number, a safe prime, the thirteenth supersingular prime, and the sixth Lucas prime. Forty-seven is a highly cototient number... |
48 48 (number) 48 is the natural number following 47 and preceding 49. It is one third of a gross or four dozens.- In mathematics :Forty-eight is a double factorial of 6, a highly composite number. Like all other multiples of 6, it is a semiperfect number. 48 is the second 17-gonal number.48 is in abundance... |
49 49 (number) 49 is the natural number following 48 and preceding 50.-In mathematics:* Forty-nine is the square of seven and is therefore the fourth squared prime number.The aliquot sum of forty-nine is 8... |
| 50 50 (number) This article discusses the number fifty. For the year 50 CE, see 50. For other uses of 50, see 50 50 is the natural number following 49 and preceding 51.-In mathematics:... |
51 | 52 52 (number) 52 is the natural number following 51 and preceding 53.-In mathematics:Fifty-two is the 6th Bell number and a decagonal number... |
53 53 (number) 53 is the natural number following 52 and preceding 54.-In mathematics:Fifty-three is the 16th prime number. It is also an Eisenstein prime.... |
54 54 (number) 54 is the natural number following 53 and preceding 55.-In mathematics:54 is a 19-gonal number. Twice the third power of three, 54 is a Leyland number. 54 can be written as the sum of three squares in three different ways: 7^2 + 2^2 + 1^2 = 6^2 + 2 = 2 + 2^2 = 54. It is the smallest number with... |
55 55 (number) 55 is the natural number following 54 and preceding 56.-Albania:*Gazeta 55, a newspaper*Constitution law 55, a law during Communist Albania.-Mathematics:... |
56 56 (number) 56 is the natural number following 55 and preceding 57.- Mathematics :56 is the sum of the first six triangular numbers , as well as the sum of six consecutive primes . It is also a tetranacci number and a pronic number. Adding up the divisors of 1 through 8 gives 56... |
57 57 (number) 57 is the natural number following 56 and preceding 58.- In mathematics :Fifty-seven is the sixteenth discrete semiprime and the sixth in the family. With 58 it forms the fourth discrete bi-prime pair. 57 has an aliquot sum of 23 and is the first composite member of the 23-aliquot tree... |
58 58 (number) 58 is the natural number following 57 and preceding 59.-In mathematics:Fifty-eight has an aliquot sum of 32 and is the second composite member of the 83-aliquot tree.... |
59 59 (number) 59 is the natural number following 58 and preceding 60.-In mathematics:Fifty-nine is the 17th smallest prime number. The next is sixty-one, with which it comprises a twin prime. 59 is an irregular prime, a safe prime and the 14th supersingular prime. It is an Eisenstein prime with no imaginary... |
| 60 60 (number) 60 is the natural number following 59 and preceding 61. Being three times twenty, 60 is called "three score" in some older literature.-In mathematics:... |
61 61 (number) 61 is the natural number following 60 and preceding 62.-In mathematics:It is the 18th prime number. The previous is 59, with which it comprises a twin prime. Sixty-one is a cuban prime of the form p = / , x = y + 1.... |
62 62 (number) 62 is a natural number following 61 and preceding 63. It is a composite number with the divisors 2 and 31 being the eighteenth discreet semiprime. 62 has an aliquot sum of 34; itself a discrete semiprime, and the 10 member aliquot sequence . 62 is therefore the tenth member of the 7-aliquot tree... |
63 63 (number) 63 is a natural number following 62 and preceding 64.-In mathematics:Although a number of the form 2n - 1, 63 is not a Mersenne prime since n is not prime and 63 is certainly not prime either. It is a Woodall number and a Harshad number. It is a highly cototient number. It is a repdigit in base 4... |
64 64 (number) 64 is the natural number following 63 and preceding 65.-In mathematics:Sixty-four is the square of 8, the cube of 4, and the sixth power of 2. It is the smallest number with exactly seven divisors. It is the lowest positive power of two that is adjacent to neither a Mersenne prime nor a Fermat... |
65 65 (number) 65 is the natural number following 64 and preceding 66.-In mathematics:Sixty-five is the 23rd semiprime and the 3rd of the form it is an octagonal number. It is also a Cullen number... |
66 66 (number) 66 is the natural number following 65 and preceding 67.Usages of this number include:-Mathematics:*66 is a sphenic number, a triangular number, a hexagonal number, and a semi-meandric number... |
67 67 (number) 67 is the natural number following 66 and preceding 68. It is an odd number.-In mathematics:Sixty-seven is the 19th prime number , an irregular prime, a lucky prime, the sum of five consecutive primes , and a Heegner number.Since 18! + 1 is divisible by 67 but 67 is not one more than a multiple of... |
68 68 (number) 68 is the natural number following 67 and preceding 69.-In mathematics:Sixty-eight is a nontotient. It is also a Perrin number, preceded in the sequence by 29, 39, 51... |
69 69 (number) 69 is a number following 68 and preceding 70.- In mathematics:The aliquot sum of sixty-nine is 27 within the aliquot sequence 69 being the third composite number in the 13-aliquot tree.69 is a semiprime... |
| 70 70 (number) 70 is the natural number following 69 and preceding 71.-In mathematics:Its factorization makes it a sphenic number. 70 is a Pell number and a generalized heptagonal number, one of only two numbers to be both. Also, it is the seventh pentagonal number and the fourth 13-gonal number, as well as the... |
71 71 (number) 71 is the natural number following 70 and preceding 72.-In mathematics:71 is the algebraic degree of Conway's constant, a remarkable number arising in the study of look-and-say sequences.... |
72 72 (number) 72 is the natural number following 71 and preceding 73. It is half a gross or 6 dozen .-In mathematics:... |
73 73 (number) 73 is the natural number following 72 and preceding 74. In English, it is the smallest integer with twelve letters in its spelled out name.- In mathematics :... |
74 74 (number) 74 is the natural number following 73 and preceding 75.A seventy-four was a third-rate warship with 74 guns.-In mathematics:Seventy-four is the twenty-first distinct semiprime and the eleventh of the form 2×q... |
75 75 (number) 75 is the natural number following 74 and preceding 76.-In mathematics:As the sum of the first five pentagonal numbers, seventy-five is a pentagonal pyramidal number. It is also an enneagonal number.... |
76 76 (number) 76 is the natural number following 75 and preceding 77.-In mathematics:Seventy-six is a Lucas number, an automorphic number, a nontotient, a 14-gonal number, and a centered pentagonal number.... |
77 77 (number) 77 is the natural number following 76 and preceding 78. Seventy-seven is the smallest positive integer requiring five syllables in English.-In mathematics:... |
78 78 (number) 78 is the natural number following 77 and followed by 79.-In mathematics:78 is a triangular number, and its factorization makes it a sphenic number... |
79 79 (number) Seventy-nine is the natural number following 78 and preceding 80.79 may represent:-In mathematics:*An odd number*The smallest number that can't be represented as a sum of fewer than 19 fourth powers*A strictly non-palindromic number... |
| 80 80 (number) 80 is the natural number following 79 and preceding 81.- In mathematics :The sum of Euler's totient function φ over the first sixteen integers is 80.... |
81 81 (number) 81 is the natural number following 80 and preceding 82.-In mathematics:Eighty-one is the square of 9 and the fourth power of 3. Like all powers of three, 81 is a perfect totient number. It is a heptagonal number and a centered octagonal number. It is also a tribonacci number, and an open meandric... |
82 82 (number) 82 is the natural number following 81 and preceding 83.-In mathematics:Eighty-two is the twenty-third biprime and the twelfth of the form... |
83 83 (number) 83 is the natural number following 82 and preceding 84.-In mathematics:Eighty-three is the sum of three consecutive primes as well as the sum of five consecutive primes .... |
84 84 (number) 84 is the natural number following 83 and preceding 85.- In mathematics :Eighty-four is the sum of the first seven triangular numbers , as well as the sum of a twin prime... |
85 85 (number) 85 is the natural number following 84 and preceding 86.-In mathematics:85 is an octahedral number, a centered triangular number, a centered square number, a decagonal number, and a Smith number.... |
86 86 (number) 86 is the natural number following 85 and preceding 87.-In mathematics:86 is the 25th distinct semiprime and the 13th of the form... |
87 87 (number) 87 is the natural number following 86 and preceding 88.-In mathematics:Eighty-seven is the twenty-sixth distinct semiprime and the eighth of the form . The aliquot sum of 87 is 33 within the aliquot sequence 86 being the eighteenth composite number in the 3-aliquot tree.Eighty-seven is the sum of... |
88 88 (number) 88 is the natural number following 87 and preceding 89.- In mathematics :Eighty-Eight is a refactorable number, a primitive semiperfect number and an untouchable number... |
89 |
| 90 90 (number) 90 is the natural number preceded by 89 and followed by 91.- In mathematics :*Because 90 is the sum of its unitary divisors , it is a unitary perfect number, and because it is equal to the sum of a subset of its divisors, it is a semiperfect number. 90 is a pronic number. But it is also a... |
91 91 (number) 91 is the natural number following 90 and preceding 92.-In mathematics:Ninety-one is the twenty-seventh distinct semiprime and the second of the form... |
92 92 (number) 92 is the natural number following 91 and preceding 93.- In mathematics:Ninety-two is a pentagonal number.There are 92 Johnson solids... |
93 93 (number) 93 is the natural number following 92 and preceding 94.-In mathematics:Ninety-three is the twenty-eighth distinct semiprime and the ninth of the form... |
94 94 (number) 94 is the natural number following 93 and preceding 95.-In mathematics:Ninety-four is the twenty-ninth distinct semiprime and the fourteenth of the form... |
95 95 (number) 95 is the natural number following 94 and preceding 96.-In mathematics:Ninety-five is the thirtieth distinct semiprime and the fifth of the form... |
96 96 (number) 96 is the natural number following 95 and preceding 97.-In mathematics:Ninety-six is an octagonal number, a refactorable number and an untouchable number. Since it is a multiple of 6, it is a semiperfect number... |
97 97 (number) 97 is the natural number following 96 and preceding 98.-In mathematics:97 is the 25th prime number , following 89 and preceding 101. 97 is a Proth prime as it is 3 × 25 + 1.The numbers 97, 907, 9007, 90007 and 900007 are happy primes... |
98 98 (number) 98 is the natural number following 97 and preceding 99.-In astronomy:* Messier 98, a magnitude 11.0 spiral galaxy in the constellation Coma Berenices.... |
99 99 (number) 99 is the natural number following 98 and preceding 100.-Mathematics:99 is the ninth repdigit, a palindromic number and a Kaprekar number... |
| 100 100 (number) 100 is the natural number following 99 and preceding 101.-In mathematics:One hundred is the square of 10... |
101 101 (number) 101 is the natural number following 100 and preceding 102.It is variously pronounced "one hundred and one" / "a hundred and one", "one hundred one" / "a hundred one", and "one oh one"... |
102 102 (number) 102 is the natural number following 101 and preceding 103.-In mathematics:102 is an abundant number and semiperfect number. It is a sphenic number... |
103 103 (number) 103 is the natural number following 102 and preceding 104.-In mathematics:One hundred [and] three is the 27th prime number. The previous prime is 101, making them both twin primes... |
104 104 (number) 104 is the natural number following 103 and preceding 105.- In mathematics :One hundred [and] four is a primitive semiperfect number and a composite number, with its divisors being 1, 2, 4, 8, 13, 26, 52 and 104. As it has 8 divisors total, and 8 is one of those divisors, 104 is a refactorable... |
105 105 (number) 105 is the natural number following 104 and preceding 106.-In mathematics:105 is a triangular number, a 12-gonal number and a Zeisel number. It is a sphenic number, and is the product of three consecutive prime numbers. 105 is the double factorial of 7... |
106 106 (number) 106 is the natural number following 105 and preceding 107.-In mathematics:106 is the thirty-first distinct biprime and the fifteenth of the form... |
107 107 (number) 107 is the natural number following 106 and preceding 108.-In mathematics:One hundred [and] seven is the 28th prime number. The next prime is 109, with which it comprises a twin prime, making 107 a Chen prime.... |
108 108 (number) 108 is the natural number following 107 and preceding 109.- In mathematics :One hundred [and] eight is an abundant number and a semiperfect number... |
109 109 (number) 109 is the natural number following 108 and preceding 110.-In mathematics:One hundred [and] nine is the 29th prime number, and also a Chen prime. The previous prime is 107, making them both twin primes... |
| 110 110 (number) 110 is the natural number following 109 and preceding 111.It is also known as "eleventy", a term made famous by linguist and author J. R. R... |
111 111 (number) 111 is the natural number following 110 and preceding 112. It is the lowest positive integer requiring six syllables to name in American English, or seven syllables in Canadian and British English... |
112 112 (number) 112 is the natural number following 111 and preceding 113.-In mathematics:One hundred [and] twelve is an abundant number and a heptagonal number... |
113 113 (number) 113 is the natural number following 112 and preceding 114.-In mathematics:One hundred [and] thirteen is the 30th prime number, following 109 and preceding 127, a Sophie Germain prime, a Chen prime and a Proth prime as it is a prime number of the form 7 × 24 + 1... |
114 114 (number) 114 is the natural number following 113 and preceding 115.-In mathematics:*One hundred [and] fourteen is an abundant number, a sphenic number and a Harshad number. It is the sum of the first four hyperfactorials, including H... |
115 115 (number) 115 is the natural number following 114 and preceding 116.-In mathematics:115 is a heptagonal pyramidal number and a lucky number.... |
116 116 (number) 116 is the natural number following 115 and preceding 117.-In mathematics:116 is a noncototient, meaning that there is no solution to the equation , where stands for Euler's totient function. 116! + 1 is prime... |
117 117 (number) 117 is the natural number following 116 and preceding 118.-In mathematics:One hundred seventeen is the smallest possible length of the longest side of a Heronian tetrahedron .117 is a pentagonal number.In base 10, it is a Harshad number.-In other fields:One hundred seventeen is also:* The... |
118 118 (number) 118 is the natural number following 117 and preceding 119.-In mathematics:There is no answer to the equation φ = 118, making 118 a nontotient.118 is the smallest n such that the range n, n + 1, ..... |
119 119 (number) 119 is the natural number following 118 and preceding 120.- Mathematics :* 119 is a Perrin number, preceded in the sequence by 51, 68, 90 .... |
| 120 120 (number) 120 is the natural number following 119 and preceding 121. 120 was known as "the great hundred", especially prior to the year 1700, from the Teutonic Hundert which equalled 120. The number 100, now known commonly as "one hundred" was then known as "the small hundred". It is also known as... |
121 121 (number) 121 is the natural number following 120 and preceding 122.-In mathematics:One hundred [and] twenty-one is a square and is the sum of three consecutive primes . There are no squares besides 121 known to be of the form 1 + p + p^2 + p^3 + p^4, where p is prime... |
122 122 (number) 122 is the natural number following 121 and preceding 123.-In mathematics:It is a nontotient since there is no integer with exactly 122 coprimes below it... |
123 123 (number) 123 is the natural number following 122 and preceding 124.-In mathematics:* 123 is a Lucas number... |
124 124 (number) 124 is the natural number following 123 and preceding 125.-In mathematics:124 is the sum of eight consecutive primes... |
125 125 (number) 125 is the natural number following 124 and preceding 126.-In mathematics:One hundred [and] twenty-five is the cube of 5.... |
126 126 (number) 126 is the natural number following 125 and preceding 127.-In mathematics:One hundred [and] twenty-six is a pentagonal pyramidal number, and a decagonal number as well as a pentatope number.... |
127 127 (number) 127 is the natural number following 126 and preceding 128.- In mathematics :*As a Mersenne prime, 127 is related to the perfect number 8128. 127 is also an exponent for the Mersenne prime 2127 - 1, making 127 a double Mersenne prime... |
128 128 (number) 128 is the natural number following 127 and preceding 129.-In mathematics:One hundred [and] twenty-eight is the seventh power of 2. It is the largest number which cannot be expressed as the sum of any number of distinct squares... |
129 129 (number) 129 is the natural number following 128 and preceding 130.-In mathematics:129 is the sum of the first ten prime numbers... |
| 130 130 (number) 130 is the natural number following 129 and preceding 131.-In mathematics:130 is a sphenic number. It is a noncototient since there is no answer to the equation x - φ = 130.... |
131 131 (number) 131 is the natural number following 130 and preceding 132.-In mathematics:131 is a Sophie Germain prime, the second 3-digit palindromic prime, and also a permutable prime with 113 and 311. It can be expressed as the sum of three consecutive primes, 131 = 41 + 43 + 47. 131 is an Eisenstein prime... |
132 132 (number) 132 is the natural number following 131 and preceding 133.-In mathematics:132 is the sixth Catalan number. It is a pronic number, the product of 11 and 12. As it has 12 divisors total, 132 is a refactorable number.... |
133 133 (number) 133 is the natural number following 132 and preceding 134.-In mathematics:133 is an n whose divisors added up divide φ. It is an octagonal number and a Harshad number... |
134 134 (number) 134 is the natural number following 133 and preceding 135.-In mathematics:134 is a nontotient since there is no integer with exactly 134 coprimes below it. And it is a noncototient since there is no integer with 134 integers with common factors below it... |
135 135 (number) 135 is the natural number following 134 and preceding 136.-In mathematics:This number in base 10 can be expressed in operations using its own digits in at least two different ways... |
136 136 (number) 136 is the natural number following 135 and preceding 137.-In mathematics:136 is itself a factor of the Eddington number... |
137 137 (number) 137 is the natural number following 136 and preceding 138.-In mathematics :One hundred [and] thirty-seven is the 33rd prime number; the next is 139, with which it comprises a twin prime, and thus 137 is a Chen prime. 137 is an Eisenstein prime with no imaginary part and a real part of the form 3n -... |
138 138 (number) 138 is the natural number following 137 but before 139.-In mathematics:* Its factorization makes 138 a sphenic number* The sum of four consecutive primes... |
139 139 (number) 139 is the natural number following 138 and preceding 140.-In mathematics:One hundred [and] thirty-nine is the 34th prime number, so it is divisible only by itself and 1. It is a twin prime with 137. Because 141 is a semiprime, 139 is a Chen prime... |
| 140 140 (number) 140 is the natural number following 139 and preceding 141.-In mathematics:140 is an abundant number and a harmonic divisor number... |
141 141 (number) 141 is the natural number following 140 and preceding 142.-In mathematics:141 is a centered pentagonal number. It is the sum of the sums of divisors of the first thirteen integers.... |
142 142 (number) 142 is the natural number following 141 and preceding 143.-In astrophysics:* 142 Polana is a dark Main belt asteroid* HD 142 is a 6th magnitude star in the Phoenix constellation-In business and accounting:... |
143 143 (number) 143 is the natural number following 142 and preceding 144.-In mathematics:143 is the sum of three consecutive primes , as well as the sum of seven consecutive primes... |
144 144 (number) 144 is the natural number following 143 and preceding 145. 144 is a dozen dozens, or one gross.-In mathematics:It is the twelfth Fibonacci number, and the largest one to also be a square, as the square of 12 , following 89 and preceding 233.144 is the smallest number with exactly 15 divisors.144 is... |
145 145 (number) 145 is the natural number following 144 and preceding 146.- In mathematics :* Although composite, 145 is a pseudoprime.* Given 145, the Mertens function returns 0.* 145 is a pentagonal number and a centered square number.... |
146 146 (number) 146 is the natural number following 145 and preceding 147.-In mathematics:146 is an octahedral number as well as a composite number.... |
147 147 (number) 147 is the natural number following 146 and preceding 148.-In mathematics:There are 147 one-sided 6-polyhexes.The digits forming 147 also form the left-hand column of a normal decimal numeric keypad.... |
148 148 (number) 148 is the natural number following 147 and before 149.-In mathematics:* 148 is the second number to be both a heptagonal number and a centered heptagonal number * 148 is the twelfth member of the Mian–Chowla sequence... |
149 149 (number) 149 is the natural number between 148 and 150. It is also a prime number.-In mathematics:*149 is the 35th prime number, and with the next prime number, 151, is a twin prime, thus 149 is a Chen prime. 149 is a strong prime in the sense that it is more than the arithmetic mean of its two neighboring... |
| 150 150 (number) 150 is the natural number following 149 and preceding 151.- In mathematics :*150 is the sum of eight consecutive primes... |
151 151 (number) 151 is a natural number. It follows 150 and precedes 152.-In mathematics:151 is the 36th prime number, the previous is 149, with which it comprises a twin prime. 151 is also a palindromic prime. 151 is a centered decagonal number... |
152 152 (number) 152 is the natural number following 151 and preceding 153.-In mathematics:152 is the sum of four consecutive primes... |
153 153 (number) One hundred fifty-three is the natural number following one hundred fifty-two and preceding one hundred fifty-four.-Mathematical properties:... |
154 154 (number) One hundred and fifty-four is the natural number following one hundred and fifty-three and preceding one hundred and fifty-five.-In mathematics:* 154 is a nonagonal number... |
155 155 (number) 155 is the natural number following 154 and preceding 156. It is a composite number.... |
156 156 (number) 156 is the number equal to 100 + 50 + 6, following 155 and followed by 157.-In mathematics:It is a pronic number, a dodecagonal number, a refactorable number and a Harshad number.156 is a repdigit in base 5 .-In the military:... |
157 157 (number) 157 is the number equal to 100 + 50 + 7, following 156 and preceding 158.-In mathematics:* 157 is a prime number. The next prime is 163 and the previous prime is 151, which with 157 form a sexy prime triplet. Taking the arithmetic mean of those primes yields 157, thus it is a balanced prime.* In... |
158 158 (number) 158 is an even whole number following 157 and preceding 159.-In mathematics:* 158 is a nontotient, since there is no integer with 158 coprimes below it.* 158 is a Perrin number, appearing after 68, 90, 119.... |
159 159 (number) 159 is a natural number following 158 and preceding 160.-In mathematics:* 159 is the sum of 3 consecutive prime numbers: 47 + 53 + 59* The previous prime number is 157, and the next is 163* Given 159, the Mertens function returns 0... |
| 160 160 (number) 160 is the natural number following 159 and preceding 161.-In mathematics:* 160 is the sum of the first 11 primes, as well as the sum of the cubes of the first three primes* Given 160, the Mertens function returns 0... |
161 161 (number) 161 is an odd natural number between 160 and 162-In geography:* Bahrain and Brunei each have coastlines that are 161 kilometers in length.* Bhutan ranks #161 in world population... |
162 162 (number) 162 is an even natural number between 161 and 163.-In mathematics:162 is divisible by 2, 3, 6, 9, 18, 27, 54, and 81. But there is no positive integer such that its divisors add up to 162, hence 162 is an untouchable number.... |
163 163 (number) 163 is the natural number following 162 and preceding 164.-In mathematics:163 is a strong prime in the sense that it is greater than the arithmetic mean of its two neighboring primes... |
164 164 (number) 164 is the natural number following 163 and preceding 165.-In mathematics:* 164 is an even number* 164 is a composite number* 164 is a zero of the Mertens function* 164 is the sum of two squares, 10^2 + 8^2.... |
165 165 (number) 165 is the natural number following 164 and preceding 166.-In mathematics:* 165 is an odd number* 165 is a composite number* 165 is a deficient number* 165 is a binary palindromic number * 165 is a sphenic number... |
166 166 (number) 166 is the natural number following 165 and preceding 167.-In mathematics:* 166 is an even number* 166 is a composite number and a Smith number in base 10* Given 166, the Mertens function returns 0... |
167 167 (number) 167 is the natural number following 166 and preceding 168.-In mathematics:* 167 is an odd number* 167 is a Chen prime, since the next odd number, 169, is a square of a prime... |
168 168 (number) 168 is the natural number following 167 and preceding 169.-In mathematics:* 168 is an even number* 168 is an abundant number, as 312 is greater than 168* 168 is a composite number* There are 168 primes less than 1000... |
169 169 (number) 169 is the natural number following 168 and preceding 170.-In mathematics:* 169 is an odd number* 169 is a square number. 13 x 13 = 169, and the reverse 31 x 31 = 961... |
| 170 170 (number) 170 is the natural number following 169 and preceding 171.-In mathematics:170 is the smallest n for which φ and σ are both square. But 170 is never a solution for φ, making it a nontotient... |
171 171 (number) 171 is the natural number following 170 and preceding 172.-In mathematics:* 171 is an odd number* 171 is a composite number* 171 is a deficient number* 171 is a Harshad number, divisible by the sum of its digits... |
172 172 (number) 172 is the natural number following 171 and preceding 173.-In mathematics:* 172 is an even number* 172 is a composite number* 172 is a deficient number* 172 is a noncototient integer... |
173 173 (number) 173 is the natural number following 172 and preceding 174.-In mathematics:* 173 is an odd number* 173 is a balanced prime* 173 is a deficient number* 173 is an Eisenstein prime with no imaginary part* 173 is an Odious number* 173 is a prime number... |
174 174 (number) 174 is the natural number following 173 and preceding 175.-In mathematics:* 174 is an even number* 174 is an abundant number with the abundance of 12* 174 is a composite number* 174 is a nontotient number* 174 is an odious number... |
175 175 (number) 175 is the natural number following 174 and preceding 176.-In mathematics:* 175 is an odd number* 175 is a composite number* 175 is a decagonal number, a figurate number that represents a decagon* 175 is a deficient number, as 73 is less than 175... |
176 176 (number) 176 is the natural number following 175 and preceding 177.-In mathematics:* 176 is an even number* 176 is an abundant number, as 196 is greater than 176* 176 is a cake number* 176 is a composite number... |
177 177 (number) 177 is the natural number following 176 and preceding 178.-In mathematics:* 177 is an odd number* 177 is a composite number* 177 is a deficient number, as 63 is less than 177* 177 is a Leyland number since it can be expressed as 27 + 72... |
178 178 (number) 178 is the natural number following 177 and preceding 179.-In mathematics:* 178 is an even number* 178 is a composite number* 178 is a deficient number, as 92 is less than 178* 178 is a semiprime, a product of two primes, namely 2 and 89... |
179 179 (number) 179 is the natural number following 178 and preceding 180.-In mathematics:* 179 is an odd number* 179 is a deficient number, as 1 is less than 179* 179 is a Gaussian number* 179 is an odious number* 179 is a square-free number... |
| 180 180 (number) 180 is the natural number following 179 and preceding 181.-In mathematics:180 is an abundant number, with its proper divisors summing up to 366. 180 is also a highly composite number, a positive integer with more divisors than any smaller positive integer... |
181 181 (number) 181 is the natural number between 180 and 182.-In mathematics:* 181 is an odd number* 181 is a centered number** 181 is a centered pentagonal number** 181 is a centered 12-gonal number** 181 is a centered 18-gonal number... |
182 182 (number) 182 is the natural number following 181 and preceding 183.-In mathematics:* 182 is an even number* 182 is a composite number, as it is a positive integer with a positive divisor other than one or itself* 182 is a deficient number, as 154 is less than 182... |
183 183 (number) 183 is the natural number following 182 and preceding 184.-In mathematics:* 183 is an odd number* 183 is a central polygonal number, n^2 - n + 1, where n=14 * 183 is a composite number* 183 is a deficient number, as 65 is less than 183... |
184 184 (number) 184 is the natural number following 183 and preceding 185.-In mathematics:* 184 is an even number* 184 is a composite number* 184 is a deficient number, as 176 is less than 184... |
185 185 (number) 185 is the natural number following 184 and preceding 186.-In mathematics:* 185 is an odd number* 185 is a composite number* 185 is a deficient number, as 43 is less than 185* 185 is an odious number* 185 is a square-free number... |
186 186 (number) 186 is the natural number following 185 and preceding 187.-In mathematics:* 186 is an even number* 186 is an abundant number, as 198 is greater than 186* 186 is a composite number* There is no integer with exactly 186 coprimes less than it... |
187 187 (number) 187 is the natural number following 186 and preceding 188.-In mathematics:* 187 is an odd number* 187 is a composite number* 187 is a deficient number, as 29 is less than 187* 187 is a self number* 187 is a square-free number... |
188 188 (number) 188 is the natural number following 187 and preceding 189.-In mathematics:* 188 is an even number* 188 has 6 divisors: 1, 2, 4, 47, 94, 188* 188 is a composite number* 188 is a deficient number, as 148 is less than 188* 188 is a happy number... |
189 189 (number) 189 is the natural number following 188 and preceding 190.-In mathematics:* 189 is an odd number* 189 is a centered cube number* 189 is a composite number* 189 is a deficient number, as 131 is less than 189* 189 is a heptagonal number... |
| 190 190 (number) 190 is the natural number following 189 and preceding 191.-In mathematics:* 190 is an even number* 190 is a centered nonagonal number* 190 is a composite number* 190 is a deficient number, as 170 is less than 190... |
191 191 (number) 191 is the natural number following 190 and preceding 192.-In mathematics:* 191 is an odd number* 191 is a centered 19-gonal number* 191 is a deficient number, as 1 is less than 191... |
192 192 (number) 192 is the natural number following 191 and preceding 193.-In mathematics:* 192 is an even number* 192 is the sum of ten consecutive primes... |
193 193 (number) 193 is the natural number following 192 and preceding 194.-In mathematics:* 193 is an odd number* 193 is a centered 32-gonal number* 193 is a deficient number, as 1 is less than 193* 193 is a happy number* 193 is a lucky number... |
194 194 (number) 194 is the natural number following 193 and preceding 195.-In mathematics:* 194 is an even number* 194 is a composite number* 194 is a deficient number, as 100 is less than 194... |
195 195 (number) 195 is the natural number following 194 and preceding 196.-In mathematics:* 195 is an odd number* 195 is a composite number* 195 is a deficient number, as 141 is less than 195* 195 is a Harshad number* 195 is a lucky number... |
196 196 (number) 196 is the natural number following 195 and preceding 197.-In mathematics:* 196 is an even number* 196 is an abundant number, as 203 is greater than 196* 196 is a composite number... |
197 197 (number) 197 is the natural number following 196 and preceding 198.-In mathematics:* 197 is an odd number* 197 is a prime number** 197 is a Chen prime** 197 is an Eisenstein prime with no imaginary part** 197 is a strong prime** 197 is a twin prime with 199... |
198 198 (number) 198 is the natural number following 197 and preceding 199.-In mathematics:* 198 is an even number* 198 is an abundant number, as 270 is greater than 198* 198 is a composite number* 198 is a Harshad number, divisible by the sum of its digits... |
199 199 (number) 199 is the natural number following 198 and preceding 200.-In mathematics:* 199 is an odd number* 199 is a centered triangular number* 199 is a centered 33-gonal number* 199 is a deficient number, as 1 is less than 199* 199 is a Lucas number... |
| 200 200 (number) 200 is the natural number following 199 and preceding 201.The number appears in the Padovan sequence, preceded by 86, 114, 151 .... |
201 201 (number) 201 is the natural number following 200 and preceding 202. It may be written as "two hundred one" or "two hundred and one".-In mathematics:As the two factors of 201 are both Gaussian primes, 201 is a Blum integer.201 is a Harshad number in base 10.... |
202 202 (number) 202 is the natural number following 201 and preceding 203. It may be written as "two hundred two" or "two hundred and two".-In mathematics:... |
203 203 (number) 203 is the natural number following 202 and preceding 204. It may be written as "two hundred three" or "two hundred and three".-In mathematics:203 is the 6th Bell number, i.e. it is the number of partitions of a set of size 6... |
204 204 (number) 204 is the natural number following 203 and preceding 205. It may be written as "two hundred four" or "two hundred and four".-In mathematics:... |
205 205 (number) 205 is the natural number following 204 and preceding 206. It may be written as "two hundred five" or "two hundred and five".-In other fields:* 205 Martha is a large Main belt asteroid.... |
206 206 (number) 206 is the natural number following 205 and preceding 207. It may be written as two hundred six or two hundred and six. It is both a nontotient and a noncototient. It is the lowest positive integer to employ all of the vowels once only... |
207 207 (number) 207 is the natural number following 206 and preceding 208. It may be written as "two hundred seven" or "two hundred and seven".-In other fields:* The Year 207 AD* 207 Hedda is a sizeable Main belt asteroid.... |
208 208 (number) 208 is the natural number following 207 and preceding 209. It may be written as "two hundred eight" or "two hundred and eight".-In mathematics:* 208 is a tetranacci number* 208 is the sum of the squares of the first five primes-In other fields:... |
209 209 (number) 209 is the natural number following 208 and preceding 210. It is written as "two hundred and nine".-In mathematics:* 209 is a highly cototient number* 209 is a Harshad number* 209 is a self number* 209=16+25+34+43+52+61-In other fields:... |
| 210 210 (number) 210 is the natural number following 209 and preceding 211.- In mathematics :210 is a composite number, an abundant number, and the product of the first four prime numbers , and thus a primorial... |
220 220 (number) 220 is the natural number following 219 and preceding 221.-In mathematics:It is a composite number, with its divisors being 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110, making it an amicable number with 284... |
230 230 (number) 230 is the natural number following 229 and preceding 231.-In mathematics:It is a composite number, with its divisors being 2, 5, 10, 23, 46, and 115. Its factorisation makes it a sphenic number. There is no integer with 230 coprimes below it, thus 230 is a nontotient... |
240 240 (number) 240 is the natural number following 239 and preceding 241.-In mathematics:With 20 divisors total , more than any previous number, 240 is a highly composite number, and it is also a refactorable number or tau number, since it has 20 divisors and 20 divides 240... |
250 250 (number) 250 is the natural number following 249 and preceding 251.As a Mandarin slang term, 250 is an insult meaning "stupid person" or "simpleton". The expression is based on bàndiàozi... |
260 260 (number) 260 is the magic constant of the n×n normal magic square and n-queens problem for n = 8, the size of an actual chess board.... |
270 270 (number) 270 is the natural number following 269 and preceding 271.-In mathematics:*270 is a harmonic divisor number*270 is the fourth number that is divisible by its average integer divisor... |
280 280 (number) 280 is the natural number after 279 and before 281.-In mathematics:The denominator of the eighth harmonic number, 280 is an octagonal number.There are 280 plane trees with ten nodes.... |
290 290 (number) 290 is the natural number after 289 and before 291.-In mathematics:The product of three primes, 290 is a sphenic number, and the sum of four consecutive primes . The sum of the squares of the divisors of 17 is 290... |
|
| 300 300 (number) 300 is the natural number following 299 and preceding 301.- Mathematical properties :It is a triangular number and the sum of a pair of twin primes , as well as the sum of ten consecutive primes... |
400 400 (number) 400 is the natural number following 399 and preceding 401. - Mathematical properties :400 is the square of 20.A circle is divided into 400 grads, which is equal to 360 degrees and 2π radians... |
500 500 (number) 500 is the natural number following 499 and preceding 501.- Other fields :Five hundred is also*many NASCAR races often use the number 500 at the end of their race names 500 (five hundred) is the natural number following 499 and preceding 501.- Other fields :Five hundred is also*many NASCAR races... |
600 600 (number) For the year 600, see 600 BC or 600 AD.600 is the natural number following 599 and preceding 601.-Mathematical properties:Six hundred is a composite number, an abundant number, a pronic number and a Harshad number.-In other fields:... |
700 700 (number) 700 is the natural number following 699 and preceding 701.It is the sum of four consecutive primes... |
800 800 (number) 800 is the natural number following 799 and preceding 801.It is the sum of four consecutive primes... |
900 900 (number) For the year 900, see 900 BC or 900 AD.900 is the natural number following 899 and preceding 901. It is the square of 30 and the sum of Euler's totient function for the first 54 integers... |
|||
| 1000 | 2000 2000 (number) 2000 is the natural number following 1999 and preceding 2001.Two thousand is the highest number expressible using only two unmodified characters in roman numerals .Two thousand is also:... |
3000 3000 (number) 3000 is the natural number following 2999 and preceding 3001. It is the smallest number requiring thirteen letters in English .- In other fields :... |
4000 4000 (number) 4000 is the natural number following 3999 and preceding 4001. It is a decagonal number.- Selected numbers in the range 4001–4999 :* 4005 – triangular number* 4007 – safe prime... |
5000 5000 (number) 5000 is the natural number following 4999 and preceding 5001. Five thousand is the largest isogrammic number in the English language.-Selected numbers in the range 5001–5999:* 5003 – Sophie Germain prime... |
6000 6000 (number) 6000 is the natural number following 5999 and preceding 6001.-Selected numbers in the range 6001–6999:* 6025 – Rhythm guitarist of the Dead Kennedys from June 1978 to March 1979... |
7000 7000 (number) 7000 is the natural number following 6999 and preceding 7001.-Selected numbers in the range 7001–7999:* 7021 – triangular number* 7043 – Sophie Germain prime* 7056 – 84^2... |
8000 8000 (number) 8000 is the natural number following 7999 and preceding 8001.8000 is the cube of 20, as well as the sum of four consecutive integers cubed, 113 + 123 + 133 + 143.... |
9000 9000 (number) 9000 is the natural number following 8999 and preceding 9001.-In other fields:* ISO 9000 is the ISO's standard for Quality Management System in production environments... |
|
| 10000 10000 (number) 10000 is the natural number following 9999 and preceding 10001.-Name:Many languages have a specific word for this number: In English it is myriad, in Ancient Greek , in Aramaic , in Hebrew רבבה , in Chinese , in Japanese [man], in Korean [man], and in Thai หมื่น [meun]... |
20000 20000 (number) 20,000 is the number that comes after 19,999 and before 20,001.-Selected numbers:* 20000 – round number; also in the title of Jules Verne's novel 20,000 Leagues Under The Sea... |
30000 30000 (number) 30,000 is the number that comes after 29,999 and before 30,001.-Selected numbers:* 30000 – round number* 30029 – primorial prime* 30030 – primorial* 30240 – harmonic divisor number... |
40000 40000 (number) 40,000 is the number that comes after 39,999 and before 40,001. It is the square of 200.-Selected numbers:* 40000 – round number* 40320 – smallest factorial that is not a highly composite number... |
50000 50000 (number) 50,000 is the number that comes after 49,999 and before 50,001.-Selected numbers:* 50000 – round number* 50625 – smallest fourth power that can be expressed as the sum of only five distinct fourth powers... |
60000 60000 (number) 60,000 is the number that comes after 59,999 and before 60,001.-Selected numbers:* 60000 – round number* 60049 – Leyland number* 62210 – Markov number* 62745 – Carmichael number... |
70000 70000 (number) 70,000 is the number that comes after 69,999 and before 70,001.-Selected numbers:* 70000 – round number* 71656 – pentagonal pyramidal number* 73712 – number of n-Queens Problem solutions for n = 13,... |
80000 80000 (number) 80,000 is the number that comes after 79,999 and before 80,001.-Selected numbers:* 80000 – round number* 80286 – model number of the Intel 80286 chip* 80386 – model number of the Intel 80386 chip... |
90000 90000 (number) 90,000 is the number that comes after 89,999 and before 90,001.-Selected numbers:* 90000 – sum of the cubes of the first 24 positive integers* 90625 – the only five-digit automorphic number* 93312 – Leyland number... |
|
| 100k–1M 100000 (number) One hundred thousand is the natural number following 99999 and preceding 100001. In scientific notation, it is written as 105.In South Asia, one hundred thousand is called a lakh... |
1M–10M | 10M–100M 10000000 (number) Ten million is the natural number following 9999999 and preceding 10000001.In scientific notation, it is written as 107.In South Asia, it is known as the Crore.- Selected 8-digit numbers :*10077696 = 69... |
100M–1G 100000000 (number) One hundred million is the natural number following 99999999 and preceding 100000001.In scientific notation, it is written as 108.... |
1G–10G 1000000000 (number) 1,000,000,000 is the natural number following 999,999,999 and preceding 1,000,000,001.In scientific notation, it is written as 109.... |
|||||
| 10G–100G | 100G–1000G | ||||||||
| Larger numbers Orders of magnitude (numbers) This list contains selected positive numbers in increasing order, including counts of things, dimensionless quantity and probabilities. Each number is given a name in the short scale, which is used in English speaking countries, as well as a name in the long scale, which is used in some of the... |
|||||||||
Notable integers
Other numbers that are notable for their mathematical properties or cultural meanings include:- −40, the equal point in the Fahrenheit and Celsius scales.
- −1
- 00 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, a number which quantifies a count or an amount of nullEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
size. - 2, the smallest prime number and the only even prime.
- 4242 (number)42 is the natural number immediately following 41 and directly preceding 43. The number has received considerable attention in popular culture as a result of its central appearance in The Hitchhiker's Guide to the Galaxy as the "Answer to the Ultimate Question of Life, the Universe, and...
, "the Answer to the Ultimate Question of Life, the Universe, and Everything" according to the Hitchhikers Guide to the Galaxy - 255255 (number)255 is the natural number following 254 and preceding 256.-In mathematics:Its factorization makes it a sphenic number. Since 255 = 28 - 1, it is a Mersenne number, and the fourth such number not to be a prime number...
, 28−1 - 496496 (number)Four hundred [and] ninety-six is the natural number following four hundred [and] ninety-five and preceding four hundred [and] ninety-seven.-In mathematics:...
, a perfect numberPerfect numberIn number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
. - 786786 (number)786 is the integer coming after 785 and before 787.-In mathematics:786 is a sphenic number. 50 can be partitioned into powers of two in 786 different ways ....
, regarded as sacred in the Muslim Abjad numerologyAbjad numeralsThe Abjad numerals are a decimal numeral system in which the 28 letters of the Arabic alphabet are assigned numerical values. They have been used in the Arabic-speaking world since before the 8th century Arabic numerals...
. - 17291729 (number)1729 is the natural number following 1728 and preceding 1730.1729 is known as the Hardy–Ramanujan number after a famous anecdote of the British mathematician G. H. Hardy regarding a hospital visit to the Indian mathematician Srinivasa Ramanujan...
, a taxicab numberTaxicab numberIn mathematics, the nth taxicab number, typically denoted Ta or Taxicab, is defined as the smallest number that can be expressed as a sum of two positive algebraic cubes in n distinct ways. The concept was first mentioned in 1657 by Bernard Frénicle de Bessy, and was made famous in the early 20th...
; the smallest positive integer that can be written as the sum of two positive cubes in two different ways - 65535, 216-1, the maximum number that a 16-bit16-bit-16-bit architecture:The HP BPC, introduced in 1975, was the world's first 16-bit microprocessor. Prominent 16-bit processors include the PDP-11, Intel 8086, Intel 80286 and the WDC 65C816. The Intel 8088 was program-compatible with the Intel 8086, and was 16-bit in that its registers were 16...
unsigned integerInteger (computer science)In computer science, an integer is a datum of integral data type, a data type which represents some finite subset of the mathematical integers. Integral data types may be of different sizes and may or may not be allowed to contain negative values....
can reach. - 142857142857 (number)142857 is the six repeating digits of 1/7, 0., and is the best-known cyclic number in base 10. If it is multiplied by 2, 3, 4, 5, or 6, the answer will be a cyclic permutation of itself, and will correspond to the repeating digits of 2/7, 3/7, 4/7, 5/7, or 6/7, respectively.- Calculations :- 22/7...
, a base 10 cyclic numberCyclic numberA cyclic number is an integer in which cyclic permutations of the digits are successive multiples of the number. The most widely known is 142857:For example:Multiples of these fractions exhibit cyclic permutation:...
. - 21474836472147483647The number 2,147,483,647 is the eighth Mersenne prime, equal to 231 − 1. It is one of only four known double Mersenne primes....
, 231−1, the maximum number that a 32-bit32-bitThe range of integer values that can be stored in 32 bits is 0 through 4,294,967,295. Hence, a processor with 32-bit memory addresses can directly access 4 GB of byte-addressable memory....
signed integerInteger (computer science)In computer science, an integer is a datum of integral data type, a data type which represents some finite subset of the mathematical integers. Integral data types may be of different sizes and may or may not be allowed to contain negative values....
can reach. - 98140723569814072356 (number)9814072356 or 9,814,072,356 is 99066 squared, and is the eighty-seventh and largest square number using each of the digits 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0 exactly once ....
, the largest perfect power that contains no repeated digits in base ten.
Named integers
- GoogolGoogolA googol is the large number 10100, that is, the digit 1 followed by 100 zeros:The term was coined in 1938 by 9-year-old Milton Sirotta , nephew of American mathematician Edward Kasner...
and googolplex - Graham's numberGraham's numberGraham's number, named after Ronald Graham, is a large number that is an upper bound on the solution to a certain problem in Ramsey theory.The number gained a degree of popular attention when Martin Gardner described it in the "Mathematical Games" section of Scientific American in November 1977,...
- Moser's number
- Shannon numberShannon numberThe Shannon number, named after Claude Shannon, is an estimated lower bound on the game-tree complexity of chess. Shannon calculated it as an aside in his 1950 paper "Programming a Computer for Playing Chess"...
- Hardy-Ramanujan number
- Skewes' number
- Number of the BeastNumber of the BeastThe Number of the Beast is a term in the Book of Revelation, of the New Testament, that is associated with the first Beast of Revelation chapter 13, the Beast of the sea. In most manuscripts of the New Testament and in English translations of the Bible, the number of the Beast is...
- Leviathan numberLeviathan numberThe Leviathan number in numerology is defined as the factorial of the 666th power of ten: !, which has approximately 6.65565705×10668 digits....
- Kaprekar's constant6174 (number)6174 is known as Kaprekar's constant after the Indian mathematician D. R. Kaprekar. This number is notable for the following property:#Take any four-digit number, using at least two different digits...
Prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s
A prime number is a positive integer which has exactly two divisorDivisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s: one and itself.
The first 100 prime numbers:
11 (number)
11 is the natural number following 10 and preceding 12.Eleven is the first number which cannot be counted with a human's eight fingers and two thumbs additively. In English, it is the smallest positive integer requiring three syllables and the largest prime number with a single-morpheme name...
13 (number)
13 is the natural number after 12 and before 14. It is the smallest number with eight letters in its name spelled out in English. It is also the first of the teens – the numbers 13 through 19 – the ages of teenagers....
17 (number)
17 is the natural number following 16 and preceding 18. It is prime.In spoken English, the numbers 17 and 70 are sometimes confused because they sound similar. When carefully enunciated, they differ in which syllable is stressed: 17 vs 70...
19 (number)
19 is the natural number following 18 and preceding 20. It is a prime number.In English speech, the numbers 19 and 90 are often confused. When carefully enunciated, they differ in which syllable is stressed: 19 vs 90...
23 (number)
23 is the natural number following 22 and preceding 24.- In mathematics :Twenty-three is the ninth prime number, the smallest odd prime that is not a twin prime. Twenty-three is also the fifth factorial prime, the third Woodall prime...
29 (number)
29 is the natural number following 28 and preceding 30.-In mathematics:It is the tenth prime number, and also the fourth primorial prime. It forms a twin prime pair with thirty-one, which is also a primorial prime. Twenty-nine is also the sixth Sophie Germain prime. It is also the sum of three...
>-
| 31
31 (number)
31 is the natural number following 30 and preceding 32.- In mathematics :Thirty-one is the third Mersenne prime as well as the fourth primorial prime, and together with twenty-nine, another primorial prime, it comprises a twin prime. As a Mersenne prime, 31 is related to the perfect number 496,...
37 (number)
37 is the natural number following 36 and preceding 38.-In mathematics:It is a prime number, the fifth lucky prime, the first irregular prime, the third unique prime and the third cuban prime of the form...
41 (number)
41 is the natural number following 40 and preceding 42.-In mathematics:Forty-one is the 13th smallest prime number. The next is forty-three, with which it comprises a twin prime...
43 (number)
43 is the natural number following 42 and preceding 44.- In mathematics :Forty-three is the 14th smallest prime number. The previous is forty-one, with which it comprises a twin prime, and the next is forty-seven. 43 is the smallest prime that is not a Chen prime...
47 (number)
47 is the natural number following 46 and preceding 48.-In mathematics:Forty-seven is the fifteenth prime number, a safe prime, the thirteenth supersingular prime, and the sixth Lucas prime. Forty-seven is a highly cototient number...
53 (number)
53 is the natural number following 52 and preceding 54.-In mathematics:Fifty-three is the 16th prime number. It is also an Eisenstein prime....
59 (number)
59 is the natural number following 58 and preceding 60.-In mathematics:Fifty-nine is the 17th smallest prime number. The next is sixty-one, with which it comprises a twin prime. 59 is an irregular prime, a safe prime and the 14th supersingular prime. It is an Eisenstein prime with no imaginary...
61 (number)
61 is the natural number following 60 and preceding 62.-In mathematics:It is the 18th prime number. The previous is 59, with which it comprises a twin prime. Sixty-one is a cuban prime of the form p = / , x = y + 1....
67 (number)
67 is the natural number following 66 and preceding 68. It is an odd number.-In mathematics:Sixty-seven is the 19th prime number , an irregular prime, a lucky prime, the sum of five consecutive primes , and a Heegner number.Since 18! + 1 is divisible by 67 but 67 is not one more than a multiple of...
71 (number)
71 is the natural number following 70 and preceding 72.-In mathematics:71 is the algebraic degree of Conway's constant, a remarkable number arising in the study of look-and-say sequences....
>-
| 73
73 (number)
73 is the natural number following 72 and preceding 74. In English, it is the smallest integer with twelve letters in its spelled out name.- In mathematics :...
79 (number)
Seventy-nine is the natural number following 78 and preceding 80.79 may represent:-In mathematics:*An odd number*The smallest number that can't be represented as a sum of fewer than 19 fourth powers*A strictly non-palindromic number...
83 (number)
83 is the natural number following 82 and preceding 84.-In mathematics:Eighty-three is the sum of three consecutive primes as well as the sum of five consecutive primes ....
97 (number)
97 is the natural number following 96 and preceding 98.-In mathematics:97 is the 25th prime number , following 89 and preceding 101. 97 is a Proth prime as it is 3 × 25 + 1.The numbers 97, 907, 9007, 90007 and 900007 are happy primes...
101 (number)
101 is the natural number following 100 and preceding 102.It is variously pronounced "one hundred and one" / "a hundred and one", "one hundred one" / "a hundred one", and "one oh one"...
103 (number)
103 is the natural number following 102 and preceding 104.-In mathematics:One hundred [and] three is the 27th prime number. The previous prime is 101, making them both twin primes...
107 (number)
107 is the natural number following 106 and preceding 108.-In mathematics:One hundred [and] seven is the 28th prime number. The next prime is 109, with which it comprises a twin prime, making 107 a Chen prime....
109 (number)
109 is the natural number following 108 and preceding 110.-In mathematics:One hundred [and] nine is the 29th prime number, and also a Chen prime. The previous prime is 107, making them both twin primes...
113 (number)
113 is the natural number following 112 and preceding 114.-In mathematics:One hundred [and] thirteen is the 30th prime number, following 109 and preceding 127, a Sophie Germain prime, a Chen prime and a Proth prime as it is a prime number of the form 7 × 24 + 1...
>-
|127
127 (number)
127 is the natural number following 126 and preceding 128.- In mathematics :*As a Mersenne prime, 127 is related to the perfect number 8128. 127 is also an exponent for the Mersenne prime 2127 - 1, making 127 a double Mersenne prime...
131 (number)
131 is the natural number following 130 and preceding 132.-In mathematics:131 is a Sophie Germain prime, the second 3-digit palindromic prime, and also a permutable prime with 113 and 311. It can be expressed as the sum of three consecutive primes, 131 = 41 + 43 + 47. 131 is an Eisenstein prime...
137 (number)
137 is the natural number following 136 and preceding 138.-In mathematics :One hundred [and] thirty-seven is the 33rd prime number; the next is 139, with which it comprises a twin prime, and thus 137 is a Chen prime. 137 is an Eisenstein prime with no imaginary part and a real part of the form 3n -...
139 (number)
139 is the natural number following 138 and preceding 140.-In mathematics:One hundred [and] thirty-nine is the 34th prime number, so it is divisible only by itself and 1. It is a twin prime with 137. Because 141 is a semiprime, 139 is a Chen prime...
149 (number)
149 is the natural number between 148 and 150. It is also a prime number.-In mathematics:*149 is the 35th prime number, and with the next prime number, 151, is a twin prime, thus 149 is a Chen prime. 149 is a strong prime in the sense that it is more than the arithmetic mean of its two neighboring...
151 (number)
151 is a natural number. It follows 150 and precedes 152.-In mathematics:151 is the 36th prime number, the previous is 149, with which it comprises a twin prime. 151 is also a palindromic prime. 151 is a centered decagonal number...
157 (number)
157 is the number equal to 100 + 50 + 7, following 156 and preceding 158.-In mathematics:* 157 is a prime number. The next prime is 163 and the previous prime is 151, which with 157 form a sexy prime triplet. Taking the arithmetic mean of those primes yields 157, thus it is a balanced prime.* In...
163 (number)
163 is the natural number following 162 and preceding 164.-In mathematics:163 is a strong prime in the sense that it is greater than the arithmetic mean of its two neighboring primes...
167 (number)
167 is the natural number following 166 and preceding 168.-In mathematics:* 167 is an odd number* 167 is a Chen prime, since the next odd number, 169, is a square of a prime...
173 (number)
173 is the natural number following 172 and preceding 174.-In mathematics:* 173 is an odd number* 173 is a balanced prime* 173 is a deficient number* 173 is an Eisenstein prime with no imaginary part* 173 is an Odious number* 173 is a prime number...
>-
|179
179 (number)
179 is the natural number following 178 and preceding 180.-In mathematics:* 179 is an odd number* 179 is a deficient number, as 1 is less than 179* 179 is a Gaussian number* 179 is an odious number* 179 is a square-free number...
181 (number)
181 is the natural number between 180 and 182.-In mathematics:* 181 is an odd number* 181 is a centered number** 181 is a centered pentagonal number** 181 is a centered 12-gonal number** 181 is a centered 18-gonal number...
191 (number)
191 is the natural number following 190 and preceding 192.-In mathematics:* 191 is an odd number* 191 is a centered 19-gonal number* 191 is a deficient number, as 1 is less than 191...
193 (number)
193 is the natural number following 192 and preceding 194.-In mathematics:* 193 is an odd number* 193 is a centered 32-gonal number* 193 is a deficient number, as 1 is less than 193* 193 is a happy number* 193 is a lucky number...
197 (number)
197 is the natural number following 196 and preceding 198.-In mathematics:* 197 is an odd number* 197 is a prime number** 197 is a Chen prime** 197 is an Eisenstein prime with no imaginary part** 197 is a strong prime** 197 is a twin prime with 199...
199 (number)
199 is the natural number following 198 and preceding 200.-In mathematics:* 199 is an odd number* 199 is a centered triangular number* 199 is a centered 33-gonal number* 199 is a deficient number, as 1 is less than 199* 199 is a Lucas number...
211 (number)
211 is the natural number between 210 and 212. It is also a prime number.-In mathematics:211 is an odd number.211 is a primorial prime, sum of three consecutive primes , Chen prime, centered decagonal prime, and self prime....
223 (number)
223 is the natural number between 222 and 224. It is also a prime number.-In mathematics:223 is a long prime, a strong prime, a lucky prime and a sexy prime .223 is the fourth Carol number and the third to be prime....
227 (number)
227 is the natural number between 226 and 228. It is also a prime number.-In mathematics:227 is a prime number, and a twin prime with 229 . 223 plus 4 is 227, so they are cousin primes...
229 (number)
229 is the natural number between 228 and 230. It is also a prime number.The North American telephone area code 229 is assigned to the area around the city of Albany in southwestern Georgia in North America....
>-
|233
233 (number)
233 is the natural number between 232 and 234. It is also a prime number.-In mathematics:233 is an irregular prime, a full reptend prime, a cousin prime, a Chen prime, a Fibonacci prime and a sexy prime. It is the 13th Fibonacci number. It is an Eisenstein prime of the form 3n - 1 with no...
239 (number)
239 is the natural number following 238 and preceding 240.-In mathematics:It is a prime number. The next is 241, with which it forms a pair of twin primes. 239 is a Sophie Germain prime and a Newman–Shanks–Williams prime...
241 (number)
241 is the natural number between 240 and 242. It is also a prime number.-In mathematics:241 is the larger of the twin primes . Prime twins are always of the form , with n = 1, 2, 3, ......
251 (number)
251 is the natural number between 250 and 252. It is also a prime number.-In mathematics:251 is a regular prime, an Eisenstein prime, a Chen prime, a Gaussian prime, a Sophie Germain prime, and a sexy prime....
263 (number)
263 is the natural number between 262 and 264. It is also a prime number.-In mathematics:263 is an irregular prime, an Eisenstein prime, a long prime, a Chen prime, a Gaussian prime, a happy prime, a sexy prime, a safe prime, and a Higgs prime....
269 (number)
269 is the natural number between 268 and 270. It is also a prime number.-In mathematics:269 is a regular prime, an Eisenstein prime with no imaginary part, a long prime, a Chen prime, a Pillai prime, a Pythagorean prime, a twin prime, a sexy prime, a Higgs prime, a strong prime, and a highly...
277 (number)
277 is the natural number following 276 and preceding 278.-In mathematics:277 is the fifty-ninth prime number, following 271 and preceding 281...
|283
311 (number)
311 is the natural number after 310 and before 312.-In mathematics:311 is a twin prime with 313; an Eisenstein prime with no imaginary part and real part of the form 3n - 1; a Gaussian prime with no imaginary part and real part of the form 4n - 1; and a permutable prime with 113 and 131.It can be...
313 (number)
313 is an integer following 312 and preceding 314. 313 is a:* prime number* twin prime with 311* centered square number* long prime* pythagorean prime* regular prime* palindromic prime in both decimal and binary.* truncatable prime* happy number...
|353
353 (number)
353 is the natural number between 352 and 354. It is a prime number.-In mathematics:353 is a palindromic prime, a cousin prime with 349, and a sexy prime with both 347 and 359. It is the first multidigit palindromic prime with all prime digits. Also, it is the smallest number whose 4th power is...
359 (number)
Three hundred and fifty-nine is the number directly following 358 and directly preceding 360. 359 is a prime number.-359 in mathematics:359° is one degree less than a full revolution ; this makes it a reflex angle....
|419
419 (number)
419 may refer to:*419, the year 419 C.E.*419 *Advance-fee fraud, also known as the 419 scam, the Nigerian scam, and the Nigerian money transfer fraud*Area code 419, which is the area code of the northwestern corner of Ohio...
|467
Perfect numberPerfect numberIn number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
s
A perfect number is an integer that is the sum of its positive proper divisors (all divisors except itself).The first 10 perfect numbers:
| 1 | 6 |
|---|---|
| 2 | 28 28 (number) 28 is the natural number following 27 and preceding 29.-In mathematics:It is a composite number, its proper divisors being 1, 2, 4, 7, and 14.... |
| 3 | 496 496 (number) Four hundred [and] ninety-six is the natural number following four hundred [and] ninety-five and preceding four hundred [and] ninety-seven.-In mathematics:... |
| 4 | 8 128 8128 (number) 8128 is the natural number following 8127 and preceding 8129.It is most notable for being a perfect number, and one of the earliest numbers to be recognized as such. As a perfect number, it is tied to the Mersenne prime 127, 27 − 1, with 26 · yielding 8128... |
| 5 | 33 550 336 |
| 6 | 8 589 869 056 |
| 7 | 137 438 691 328 |
| 8 | 2 305 843 008 139 952 128 |
| 9 | 2 658 455 991 569 831 744 654 692 615 953 842 176 |
| 10 | 191 561 942 608 236 107 294 793 378 084 303 638 130 997 321 548 169 216 |
Cardinal numberCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s
In the following tables, [and] indicates that the word and is used in some dialectDialect
The term dialect is used in two distinct ways, even by linguists. One usage refers to a variety of a language that is a characteristic of a particular group of the language's speakers. The term is applied most often to regional speech patterns, but a dialect may also be defined by other factors,...
s (such as British English
British English
British English, or English , is the broad term used to distinguish the forms of the English language used in the United Kingdom from forms used elsewhere...
), and omitted in other dialects (such as American English
American English
American English is a set of dialects of the English language used mostly in the United States. Approximately two-thirds of the world's native speakers of English live in the United States....
).
Small numbers
This table demonstrates the standard English construction of small cardinal numbers up to one hundred million—names for which all variants of English agree.| Value | Name | Alternate names, and names for sets of the given size |
|---|---|---|
| 0 | Zero Names for the number 0 There are several names for the number 0 in English, and concomitant names for the decades where the tens column contains the number 0. Several names for the number 0 include "zero", "cipher", "naught", "nought", "love", "duck", "nil", "zilch", "zip", and "o"... |
aught, cipher, cypher, goose egg, love, nada, naught, nil, none, nought, nowt, null, ought, oh, squat, zed, zilch, zip |
| 1 | One | ace, single, singleton, unary, unit, unity |
| 2 | Two | binary, brace, couple, couplet, distich, deuce, double, doubleton, duad, duality, duet, duo, dyad, pair, span, twain, twosome, yoke |
| 3 | Three | deuce-ace, leash, set, tercet, ternary, ternion, terzetto, threesome, tierce, trey, triad, trine, trinity, trio, triplet, troika, hat-trick |
| 4 | Four | foursome, quadruplet, quatern, quaternary, quaternion, quaternity, quartet, tetrad |
| 5 | Five | cinque, fin, fivesome, pentad, quint, quintet, quintuplet |
| 6 | Six | half dozen, hexad, sestet, sextet, sextuplet, sise |
| 7 | Seven | heptad, septet, septuple |
| 8 | Eight | octad, octave, octet, octonary, octuplet, ogdoad |
| 9 | Nine | ennead |
| 10 | Ten | deca, decade |
| 11 | Eleven | onze, ounze, ounce |
| 12 | Twelve | dozen |
| 13 | Thirteen | baker's dozen, long dozen |
| 14 | Fourteen | |
| 15 | Fifteen | |
| 16 | Sixteen | |
| 17 | Seventeen | |
| 18 | Eighteen | |
| 19 | Nineteen | |
| 20 | Twenty | score |
| 21 | Twenty-one | long score |
| 22 | Twenty-two | Deuce-deuce |
| 23 | Twenty-three | |
| 24 | Twenty-four | two dozen |
| 25 | Twenty-five | |
| 26 | Twenty-six | |
| 27 | Twenty-seven | |
| 28 | Twenty-eight | |
| 29 | Twenty-nine | |
| 30 | Thirty | |
| 31 | Thirty-one | |
| 40 | Forty | |
| 50 | Fifty | half-century |
| 60 | Sixty | three-score |
| 70 | Seventy | three-score and ten |
| 80 | Eighty | four-score |
| 87 | Eighty-seven | four-score and seven Gettysburg Address The Gettysburg Address is a speech by U.S. President Abraham Lincoln and is one of the most well-known speeches in United States history. It was delivered by Lincoln during the American Civil War, on the afternoon of Thursday, November 19, 1863, at the dedication of the Soldiers' National Cemetery... |
| 90 | Ninety | |
| 100 | One hundred | centred, century, ton, short hundred |
| 101 | One hundred [and] one | |
| 110 | One hundred [and] ten | |
| 111 | One hundred [and] eleven | |
| 120 | One hundred [and] twenty | long hundred, great hundred, (obsolete) hundred |
| 121 | One hundred [and] twenty-one | |
| 144 | One hundred [and] forty-four | gross Gross (unit) A gross is equal to a dozen dozen, i.e. 12 × 12 = 144.It can be used in duodecimal counting. The use of gross likely originated from the fact that 144 can be counted on the fingers using the fingertips and first two joints of each finger when marked by the thumb of one hand. The other hand... , dozen dozen, small gross |
| 169 | One hundred [and] sixty-nine | baker's gross |
| 200 | Two hundred | |
| 300 | Three hundred | |
| 666 | Six Hundred [and] sixty-six | Number of the Beast Number of the Beast The Number of the Beast is a term in the Book of Revelation, of the New Testament, that is associated with the first Beast of Revelation chapter 13, the Beast of the sea. In most manuscripts of the New Testament and in English translations of the Bible, the number of the Beast is... |
| 1 000 | One thousand | chiliad, grand, G, thou, yard, kilo, k |
| 1 001 | One thousand [and] one | |
| 1 010 | One thousand [and] ten | |
| 1 011 | One thousand [and] eleven | |
| 1 024 | One thousand [and] twenty-four | kibi or kilo in computing Computing Computing is usually defined as the activity of using and improving computer hardware and software. It is the computer-specific part of information technology... , see binary prefix Binary prefix In computing, a binary prefix is a specifier or mnemonic that is prepended to the units of digital information, the bit and the byte, to indicate multiplication by a power of 2... (kilo is shortened to K, Kibi to Ki) |
| 1 100 | One thousand one hundred | Eleven hundred |
| 1 101 | One thousand one hundred [and] one | |
| 1 728 | One thousand seven hundred [and] twenty-eight | great gross, long gross, dozen gross |
| 2 000 | Two thousand | |
| 10 000 | Ten thousand | myriad Myriad Myriad , "numberlesscountless, infinite", is a classical Greek word for the number 10,000. In modern English, the word refers to an unspecified large quantity.-History and usage:... , wan (China) |
| 100 000 | One hundred thousand | lakh Lakh A lakh is a unit in the Indian numbering system equal to one hundred thousand . It is widely used both in official and other contexts in Pakistan, Bangladesh, India, Maldives, Nepal, Sri Lanka, Myanmar and is often used in Indian English.-Usage:... |
| 500 000 | Five hundred thousand | crore Crore A crore is a unit in the Indian number system equal to ten million , or 100 lakhs. It is widely used in India, Bangladesh, Nepal, and Pakistan.... (Iranian) |
| 1 000 000 | One million | Mega, meg, mil, (often shortened to M) |
| 1 048 576 | One million forty-eight thousand five hundred [and] seventy-six | Mibi or Mega in computing Computing Computing is usually defined as the activity of using and improving computer hardware and software. It is the computer-specific part of information technology... , see binary prefix Binary prefix In computing, a binary prefix is a specifier or mnemonic that is prepended to the units of digital information, the bit and the byte, to indicate multiplication by a power of 2... (Mega is shortened to M, Mibi to Mi) |
| 10 000 000 | Ten million | crore Crore A crore is a unit in the Indian number system equal to ten million , or 100 lakhs. It is widely used in India, Bangladesh, Nepal, and Pakistan.... (Bhartia) |
| 100 000 000 | One hundred million | yi (China) |
English names for powers of 10
This table compares the English names of cardinal numbers according to various American, British, and Continental European conventions. See English numerals or names of large numbersNames of large numbers
This article lists and discusses the usage and derivation of names of large numbers, together with their possible extensions.The following table lists those names of large numbers which are found in many English dictionaries and thus have a special claim to being "real words"...
for more information on naming numbers.
| Short scale Long and short scales The long and short scales are two of several different large-number naming systems used throughout the world for integer powers of ten. Many countries, including most in continental Europe, use the long scale whereas most English-speaking countries use the short scale... | | Long scale Long and short scales The long and short scales are two of several different large-number naming systems used throughout the world for integer powers of ten. Many countries, including most in continental Europe, use the long scale whereas most English-speaking countries use the short scale... | | Power | |||
|---|---|---|---|---|---|
| Value | American | British (Nicolas Chuquet Nicolas Chuquet Nicolas Chuquet was a French mathematician whose great work, Triparty en la science des nombres , was unpublished in his lifetime... ) | Continental European (Jacques Peletier du Mans Jacques Peletier du Mans Jacques Pelletier du Mans, also spelled Peletier, in Latin: Peletarius , was a humanist, poet and mathematician of the French Renaissance.... ) | of a thousand | of a million |
| 100 | One | 1000−1+1 | 10000000 | ||
| 101 | Ten | ||||
| 102 | Hundred | ||||
| 103 | Thousand | 10000+1 | 10000000.5 | ||
| 106 | Million | 10001+1 | 10000001 | ||
| 109 | Billion | Thousand million | Milliard | 10002+1 | 10000001.5 |
| 1012 | Trillion | Billion | 10003+1 | 10000002 | |
| 1015 | Quadrillion | Thousand billion | Billiard | 10004+1 | 10000002.5 |
| 1018 | Quintillion | Trillion | 10005+1 | 10000003 | |
| 1021 | Sextillion | Thousand trillion | Trilliard | 10006+1 | 10000003.5 |
| 1024 | Septillion | Quadrillion | 10007+1 | 10000004 | |
| 1027 | Octillion | Thousand quadrillion | Quadrilliard | 10008+1 | 10000004.5 |
| 1030 | Nonillion | Quintillion | 10009+1 | 10000005 | |
| 1033 | Decillion | Thousand quintillion | Quintilliard | 100010+1 | 10000005.5 |
| 1036 | Undecillion | Sextillion | 100011+1 | 10000006 | |
| 1039 | Duodecillion | Thousand sextillion | Sextilliard | 100012+1 | 10000006.5 |
| 1042 | Tredecillion | Septillion | 100013+1 | 10000007 | |
| 1045 | Quattuordecillion | Thousand septillion | Septilliard | 100014+1 | 10000007.5 |
| 1048 | Quindecillion | Octillion | 100015+1 | 10000008 | |
| 1051 | Sexdecillion | Thousand octillion | Octilliard | 100016+1 | 10000008.5 |
| 1054 | Septendecillion | Nonillion | 100017+1 | 10000009 | |
| 1057 | Octodecillion | Thousand nonillion | Nonilliard | 100018+1 | 10000009.5 |
| 1060 | Novemdecillion | Decillion | 100019+1 | 100000010 | |
| 1063 | Vigintillion | Thousand decillion | Decilliard | 100020+1 | 100000010.5 |
| 1066 | Unvigintillion | Undecillion | 100021+1 | 100000011 | |
| 1069 | Duovigintillion | Thousand undecillion | Undecilliard | 100022+1 | 100000011.5 |
| 1072 | Trevigintillion | Duodecillion | 100023+1 | 100000012 | |
| 1075 | Quattuorvigintillion | ... | ... | 100024+1 | 100000012.5 |
| ... | ... | ... | ... | ... | |
| 1093 | Trigintillion | Thousand quindecillion | Quindecilliard | 100030+1 | 100000015.5 |
| ... | ... | ... | ... | ... | |
| 10120 | Novemtrigintillion | Vigintillion | 100039+1 | 100000020 | |
| 10123 | Quadragintillion | Thousand vigintillion | Vigintilliard | 100040+1 | 100000020.5 |
| ... | ... | ... | ... | ... | |
| 10153 | Quinquagintillion | Thousand quinvigintillion | Quinvigintilliard | 100050+1 | 100000025.5 |
| ... | ... | ... | ... | ... | |
| 10180 | Novemquinquagintillion | Trigintillion | 100059+1 | 100000030 | |
| 10183 | Sexagintillion | Thousand trigintillion | Trigintilliard | 100060+1 | 100000030.5 |
| ... | ... | ... | ... | ... | |
| 10213 | Septuagintillion | Thousand quintrigintillion | Quintrigintilliard | 100070+1 | 100000035.5 |
| ... | ... | ... | ... | ... | |
| 10240 | Novemseptuagintillion | Quadragintillion | 100079+1 | 100000040 | |
| 10243 | Octogintillion | Thousand quadragintillion | Quadragintilliard | 100080+1 | 100000040.5 |
| ... | ... | ... | ... | ... | |
| 10273 | Nonagintillion | Thousand quinquadragintillion | Quinquadragintilliard | 100090+1 | 100000045.5 |
| ... | ... | ... | ... | ... | |
| 10300 | Novemnonagintillion | Quinquagintillion | 100099+1 | 100000050 | |
| 10303 | Centillion Centillion Centillion is a big number. It refers to different quantities based on locality of usage.- North American system :* In Canadian and U.S. usage, two centillion is 10303+10303.... |
Thousand quinquagintillion | Quinquagintilliard | 1000100+1 | 100000050.5 |
| ... | ... | ... | ... | ||
| 10360 | Sexagintillion | 1000119+1 | 100000060 | ||
| 10420 | Septuagintillion | 1000139+1 | 100000070 | ||
| 10480 | Octogintillion | 1000159+1 | 100000080 | ||
| 10540 | Nonagintillion | 1000179+1 | 100000090 | ||
| 10600 | Centillion Centillion Centillion is a big number. It refers to different quantities based on locality of usage.- North American system :* In Canadian and U.S. usage, two centillion is 10303+10303.... |
1000199+1 | 1000000100 | ||
| 10603 | Ducentillion | Thousand Centillion | Centilliard | 1000200+1 | 1000000100.5 |
There is no consistent and widely accepted way to extend cardinals beyond centillion
Centillion
Centillion is a big number. It refers to different quantities based on locality of usage.- North American system :* In Canadian and U.S. usage, two centillion is 10303+10303....
(centilliard).
Proposed systematic names for powers of 10
Myriad system
Proposed by Donald E. Knuth:
| Value | Name | Notation |
|---|---|---|
| 100 | One | 1 |
| 101 | Ten | 10 |
| 102 | Hundred | 100 |
| 103 | Ten hundred | 1000 |
| 104 | Myriad | 1,0000 |
| 105 | Ten myriad | 10,0000 |
| 106 | Hundred myriad | 100,0000 |
| 107 | Ten hundred myriad | 1000,0000 |
| 108 | Myllion | 1;0000,0000 |
| 1012 | Myriad myllion | 1,0000;0000,0000 |
| 1016 | Byllion | 1:0000,0000;0000,0000 |
| 1024 | Myllion byllion | 1;0000,0000:0000,0000;0000,0000 |
| 1032 | Tryllion | 1'0000,0000;0000,0000:0000,0000;0000,0000 |
| 1064 | Quadryllion | 1'0000,0000;0000,0000:0000,0000;0000,0000'0000,0000;0000,0000:0000,0000;0000,0000 |
| 10128 | Quintyllion | |
| 10256 | Sextyllion | |
| 10512 | Septyllion | |
| 101024 | Octyllion | |
| 102048 | Nonyllion | |
| 104096 | Decyllion | |
| 108192 | Undecyllion | |
| 1016,384 | Duodecyllion | |
| 1032,768 | Tredecyllion | |
| 1065,536 | Quattuordecyllion | |
| 10131,072 | Quindecyllion | |
| 10262,144 | Sexdecyllion | |
| 10524,288 | Septendecyllion | |
| 101,048,576 | Octodecyllion | |
| 102,097,152 | Novemdecyllion | |
| 104,194,304 | Vigintyllion | |
| 108,388,608 | Cafarolion | |
| 1016,777,216 | Saralion | |
 |
Quadragintyllion | |
 |
Quinquagintyllion | |
 |
Sexagintyllion | |
 |
Septuagintyllion | |
 |
Octogintyllion | |
 |
Nonagintyllion | |
 |
Centyllion | |
 |
Millyllion | |
 |
Myryllion | |
SI-derived
| Value | 1000m | SI prefix SI prefix The International System of Units specifies a set of unit prefixes known as SI prefixes or metric prefixes. An SI prefix is a name that precedes a basic unit of measure to indicate a decadic multiple or fraction of the unit. Each prefix has a unique symbol that is prepended to the unit symbol... | Name | Binary prefix Binary prefix In computing, a binary prefix is a specifier or mnemonic that is prepended to the units of digital information, the bit and the byte, to indicate multiplication by a power of 2... | 1024m=210m | Value |
|---|---|---|---|---|---|---|
| 1 000 | 10001 | k | Kilo Kilo Kilo- is a unit prefix in the metric system denoting multiplication of the unit by one thousand.For example:* one kilogram is 1000 grams* one kilometre is 1000 metres* one kilojoule is 1000 joules... |
Ki | 10241 | 1 024 |
| 1 000 000 | 10002 | M | Mega Mega Mega- is an prefix in the metric system denoting a factor of million . Confirmed in 1960, it comes from the Greek μέγας, meaning great.-Other common examples of usage:* megapixel - 1 million pixels in a digital camera... |
Mi | 10242 | 1 048 576 |
| 1 000 000 000 | 10003 | G | Giga Giga Giga is a unit prefix in the metric system denoting a factor of billion . It has the symbol G.Giga is derived from the Greek γίγας, meaning 'giant'... |
Gi | 10243 | 1 073 741 824 |
| 1 000 000 000 000 | 10004 | T | Tera Tera Tera- is a prefix in the metric system denoting 1012 or .The prefix tera was was confirmed in 1960. In computer science tera can sometimes mean instead of , especially in the term terabyte. To avoid this ambiguity, the binary prefix tebi has been introduced to signify 240.... |
Ti | 10244 | 1 099 511 627 776 |
| 1 000 000 000 000 000 | 10005 | P | Peta Peta Peta can refer to:* peta-, an SI prefix denoting a factor of 1015* Peta, Greece, a town in Greece* Peta, the Pāli word for a Preta, or hungry ghost in Buddhism* Peta Wilson, an Australian actress and model* Peta Todd, English glamour model... |
Pi | 10245 | 1 125 899 906 842 624 |
| 1 000 000 000 000 000 000 | 10006 | E | Exa Exa Exa- is a prefix in the metric system denoting 1018 or .Adopted in 1975, it comes from the Greek ἕξ, used as a prefix ἑξά-, meaning six , because it is equal to 10006.Examples:* 1 EeV = 1018 electronvolts = 0.1602 joule... |
Ei | 10246 | 1 152 921 504 606 846 976 |
| 1 000 000 000 000 000 000 000 | 10007 | Z | Zetta Zetta Zetta- is a prefix in the metric system denoting a factor of 1021 or .Added to the SI in 1991, it is evocative of the French numeral sept, meaning seven, because it is equal to 10007.... |
Zi | 10247 | 1 180 591 620 717 411 303 424 |
| 1 000 000 000 000 000 000 000 000 | 10008 | Y | Yotta Yotta Yotta is the largest unit prefix in the International System of Units denoting a factor of 1024 or . It has the unit symbol Y.The prefix name is derived from the Greek , meaning eight, because it is equal to 10008... |
Yi | 10248 | 1 208 925 819 614 629 174 706 176 |
FractionalFraction (mathematics)A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
numbers
This is a table of English names for positive rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s less than or equal to 1. It also lists alternative names, but there is no widespread convention for the names of extremely small positive numbers.
Keep in mind that rational numbers like 0.12 can be represented in infinitely many ways, e.g. zero-point-one-two (0.12), twelve percent (12%), three twenty-fifths
 , nine seventy-fifths
, nine seventy-fifths  , six fiftieths
, six fiftieths  , twelve hundredths
, twelve hundredths  , twenty-four two-hundredths
, twenty-four two-hundredths  , etc.
, etc.
| Value | Fraction | Common names | Alternative names |
|---|---|---|---|
| 1 |  |
One | 0.999... 0.999... In mathematics, the repeating decimal 0.999... denotes a real number that can be shown to be the number one. In other words, the symbols 0.999... and 1 represent the same number... |
| 0.9 |  |
Nine tenths, [zero] point nine | |
| 0.8 |  |
Four fifths, eight tenths, [zero] point eight | |
| 0.7 | 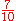 |
Seven tenths, [zero] point seven | |
| 0.6 | 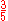 |
Three fifths, six tenths, [zero] point six | |
| 0.5 |  |
One half, five tenths, [zero] point five | |
| 0.4 |  |
Two fifths, four tenths, [zero] point four | |
| 0.3 (333 333)... | 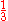 |
One third | |
| 0.3 |  |
Three tenths, [zero] point three | |
| 0.25 |  |
One quarter, one fourth, twenty-five hundredths, [zero] point two five | |
| 0.2 |  |
One fifth, two tenths, [zero] point two | |
| 0.16 (666 666)... | 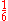 |
One sixth | |
| 0.142 857 (142 857)... |  |
One seventh | |
| 0.125 |  |
One eighth, one-hundred-[and-]twenty-five thousandths, [zero] point one two five | |
| 0.1 (111 111)... |  |
One ninth | |
| 0.1 |  |
One tenth, [zero] point one | One perdecime, one perdime |
| 0.090 (909 090)... | 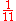 |
One eleventh | |
| 0.09 |  |
Nine hundredths, [zero] point zero nine | |
| 0.083 (333 333)... | 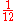 |
One twelfth | |
| 0.08 | 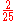 |
Two twenty-fifths, eight hundredths, [zero] point zero eight | |
| 0.0625 | 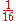 |
One sixteenth, six-hundred-[and-]twenty-five ten-thousandths, [zero] point zero six two five | |
| 0.05 | 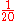 |
One twentieth, [zero] point zero five | |
| 0.047 619 (047 619)... | 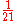 |
One twenty-first | |
| 0.045 (454 545)... | 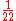 |
One twenty-second | |
| 0.043 478 260 869 565 217 3913 (043 478)... |  |
One twenty-third | |
| 0.03 (333 333)... |  |
One thirtieth | |
| 0.016 (666 666)... | 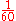 |
One sixtieth | One minute Minute A minute is a unit of measurement of time or of angle. The minute is a unit of time equal to 1/60th of an hour or 60 seconds. In the UTC time scale, a minute on rare occasions has 59 or 61 seconds; see leap second. The minute is not an SI unit; however, it is accepted for use with SI units... |
| 0.012345679 (012345679)... | 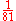 |
One eighty-first | |
| 0.01 | 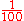 |
One hundredth, [zero] point zero one | One percent |
| 0.001 | 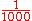 |
One thousandth, [zero] point zero zero one | One permille Permille A per mil or per mille is a tenth of a percent or one part per thousand. It is written with the sign ‰ , which looks like a percent sign with an extra zero at the end... |
| 0.000 27 (777 777)... | 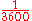 |
One thirty-six hundredth | One second |
| 0.000 1 | 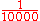 |
One ten-thousandth, [zero] point zero zero zero one | One myriadth, one permyria, one permyriad, one basis point Basis point A basis point is a unit equal to 1/100 of a percentage point or one part per ten thousand... |
| 0.000 01 | 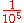 |
One hundred-thousandth | One lakhth, one perlakh |
| 0.000 001 | 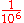 |
One millionth | One perion, one ppm |
| 0.000 000 1 | 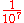 |
One ten-millionth | One crorth, one percrore |
| 0.000 000 01 | 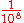 |
One hundred-millionth | One awkth, one perawk |
| 0.000 000 001 | 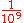 |
One billionth (in some dialects) | One ppb PPB PPB can stand for:* Party political broadcast, a type of political programming in the United Kingdom* parts-per-billion, a unit of concentration* Portland Police Bureau, a police agency for the city of Portland... |
| 0 |  |
Zero | |
Algebraic numberAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s
| Expression | Approximate value | Notes |
|---|---|---|
 |
0.433 012 701 892 219 323 381 861 585 376 | Area of a triangle with sides of length one and half its height. |
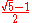 |
0.618 033 988 749 894 848 204 586 834 366 | Golden ratio conjugate  , reciprocal , reciprocalMultiplicative inverse In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the... of and one less than the golden ratio Golden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... . |
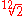 |
1.059 463 094 359 295 264 561 825 294 946 | Twelfth root of two. Proportion between the frequencies of adjacent semitone Semitone A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.... s in the equal temperament Equal temperament An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for... scale. |
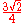 |
1.060 660 171 779 821 286 601 266 543 157 | The size of the cube that satisfies Prince Rupert's cube Prince Rupert's cube In geometry, Prince Rupert's cube is the largest cube that can pass through a hole drilled through a unit cube, i.e. through a cube whose sides have length 1. Curiously, it is slightly larger than the unit cube, with a side length of... . |
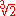 |
1.259 921 049 894 873 164 767 210 607 278 | Cube root of two. Length of the edge of a cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... with volume two. See doubling the cube Doubling the cube Doubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction... for the significance of this number. |
| n/a | 1.303 577 269 034 296 391 257 099 112 153 | Conway's constant, defined as the unique positive real root of a certain polynomial of degree 71. |
 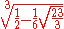 |
1.324 717 957 244 746 025 960 908 854 478 | Plastic number Plastic number In mathematics, the plastic number ρ is a mathematical constant which is the unique real solution of the cubic equationx^3=x+1\, .... , the unique real root of the cubic equation  |
 |
1.414 213 562 373 095 048 801 688 724 210 | 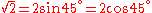 Square root of two a.k.a. Pythagoras' constant. Ratio of diagonal Diagonal A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a... to side length in a square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... . Proportion between the sides of paper size Paper size Many paper size standards conventions have existed at different times and in different countries. Today there is one widespread international ISO standard and a localised standard used in North America . The paper sizes affect writing paper, stationery, cards, and some printed documents... s in the ISO 216 ISO 216 ISO 216 specifies international standard paper sizes used in most countries in the world today. It defines the "A" and "B" series of paper sizes, including A4, the most commonly available size... series (originally DIN Din DIN or Din or din can have several meanings:* A din is a loud noise.* Dīn, an Arabic term meaning "religion" or "way of life".* Din is one of the ten aspects of the Ein Sof in Kabbalah .... 476 series). |
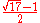 |
1.561 552 812 808 830 274 910 704 927 987 | The Triangular root of 2. |
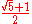 |
1.618 033 988 749 894 848 204 586 834 366 | Golden ratio Golden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...  , the larger of the two real roots of , the larger of the two real roots of 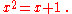 |
 |
1.732 050 807 568 877 293 527 446 341 506 |  Square root of three a.k.a. the measure of the fish Vesica piscis The vesica piscis is a shape that is the intersection of two circles with the same radius, intersecting in such a way that the center of each circle lies on the circumference of the other. The name literally means the "bladder of a fish" in Latin... . Length of the space diagonal Space diagonal In a rectangular box or a magic cube, the four space diagonals are the lines that go from a corner of the box or cube, through the center of the box or cube, to the opposite corner... of a cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... with edge length 1. Length of the diagonal of a  rectangle rectangleRectangle In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle... . Altitude Altitude (triangle) In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the... of an equilateral triangle with side length 2. Twice the altitude of an equilateral triangle with side length 1. Altitude of a regular hexagon with side length 1 and diagonal length 2. |
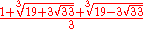 |
1.839 286 755 214 161 132 551 852 564 653 | The Tribonacci constant. Used in the formula for the volume of the snub cube Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... and properties of some of it's dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... s. It satisfies the equation x + x−3 = 2. |
 |
2.236 067 977 499 789 696 409 173 668 731 | Square root of five. Length of the diagonal Diagonal A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a... of a 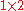 rectangle rectangleRectangle In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle... . Length of the diagonal of a  rectangle. rectangle. Length of the space diagonal of a 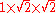 rectangular box rectangular boxCuboid In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature... . |
 |
2.414 213 562 373 095 048 801 688 724 210 | Silver ratio Silver ratio In mathematics, two quantities are in the silver ratio if the ratio between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational mathematical constant,... 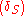 , the larger of the two real roots of , the larger of the two real roots of  |
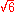 |
2.449 489 742 783 178 098 197 284 074 706 |  = area = areaArea Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat... of a 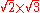 rectangle. rectangle. Length of the space diagonal Space diagonal In a rectangular box or a magic cube, the four space diagonals are the lines that go from a corner of the box or cube, through the center of the box or cube, to the opposite corner... of a  rectangular box rectangular boxCuboid In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature... . Length of the diagonal of a  rectangle rectangleRectangle In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle... . Length of the diagonal of a  rectangle. rectangle. Length of the diagonal Diagonal A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a... of a square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... with side length  . . |
 |
2.645 751 311 064 590 590 501 615 753 639 | Length of the space diagonal Space diagonal In a rectangular box or a magic cube, the four space diagonals are the lines that go from a corner of the box or cube, through the center of the box or cube, to the opposite corner... of a 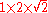 rectangular box rectangular boxCuboid In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature... . Length of the diagonal of a 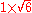 rectangle rectangleRectangle In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle... . Length of the diagonal of a 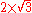 rectangle. rectangle. Length of the diagonal of a 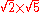 rectangle. rectangle. |
 |
2.828 427 124 746 190 097 603 377 448 419 |  Volume Volume Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains.... of a cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... with edge length  . . Length of the diagonal Diagonal A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a... of a square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... with side length 2. Length of the diagonal of a 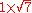 rectangle. rectangle. Length of the diagonal of a 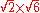 rectangle. rectangle. Length of the diagonal of a 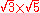 rectangle. rectangle. |
 |
3.162 277 660 168 379 331 998 893 544 433 |  = area = areaArea Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat... of a 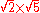 rectangle. rectangle. Length of the diagonal Diagonal A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a... of a 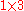 rectangle rectangleRectangle In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle... . Length of the diagonal of a 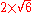 rectangle. rectangle. Length of the diagonal of a 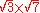 rectangle. rectangle. Length of the diagonal Diagonal A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a... of a square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... with side length  . . |
 |
3.316 624 790 355 399 849 114 932 736 671 | Length of the space diagonal Space diagonal In a rectangular box or a magic cube, the four space diagonals are the lines that go from a corner of the box or cube, through the center of the box or cube, to the opposite corner... of a 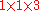 rectangular box rectangular boxCuboid In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature... . Length of the diagonal of a  rectangle rectangleRectangle In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle... . Length of the diagonal of a  rectangle. rectangle. Length of the diagonal of a 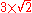 rectangle. rectangle. Length of the diagonal of a 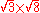 rectangle. rectangle. Length of the diagonal of a  rectangle. rectangle. |
 |
3.464 101 615 137 754 587 054 892 683 012 |  Length of the space diagonal Space diagonal In a rectangular box or a magic cube, the four space diagonals are the lines that go from a corner of the box or cube, through the center of the box or cube, to the opposite corner... of a cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... with edge length 2. Length of the diagonal of a  rectangle rectangleRectangle In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle... . Length of the diagonal of a  rectangle. rectangle. Length of the diagonal of a 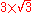 rectangle. rectangle. Length of the diagonal of a 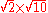 rectangle. rectangle. Length of the diagonal of a 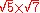 rectangle. rectangle. Length of the diagonal Diagonal A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a... of a square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... with side length  . . |
Transcendental numberTranscendental numberIn mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
s
- (−1)iImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
= e−π = 0.0432139183... - Liouville constant: c = 0.110001000000000000000001000...
- Champernowne constantChampernowne constantIn mathematics, the Champernowne constant C10 is a transcendental real constant whose decimal expansion has important properties. It is named after mathematician D. G...
: C10 = 0.12345678910111213141516... - ii = √(e−π) = 0.207879576...
- Copeland–Erdős constant: 0.235711131719232931374143...
- The logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of 2 to base 10, used to find the number of digits in a power of 2: 0.301029995663981... - The inverse of π: 0.318309886183790671537767526745028724068919291480...
- The inverse of e: 0.367879441171442321595523770161460867445811131031...
- Prouhet–Thue–Morse constant: τ = 0.412454033640...
- Omega constant: Ω = 0.5671432904097838729999686622...
- Cahen's constant: c = 0.64341054629...
- ln 2: 0.693147180559945309417232121458...
- π/√18 = 0.7404... the maximum density of sphere packing in three dimensional Euclidean space according to the Kepler conjectureKepler conjectureThe Kepler conjecture, named after the 17th-century German astronomer Johannes Kepler, is a mathematical conjecture about sphere packing in three-dimensional Euclidean space. It says that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic...
- Gauss's constantGauss's constantIn mathematics, Gauss's constant, denoted by G, is defined as the reciprocal of the arithmetic-geometric mean of 1 and the square root of 2:The constant is named after Carl Friedrich Gauss, who on May 30, 1799 discovered thatso that...
: G = 0.8346268... - π/√12 = 0.9086..., the fraction of the plane covered in circle packing
- ei+e-i = 2cos(1)Cosine similarityCosine similarity is a measure of similarity between two vectors by measuring the cosine of the angle between them. The cosine of 0 is 1, and less than 1 for any other angle. The cosine of the angle between two vectors thus determines whether two vectors are pointing in roughly the same...
= 1.08060461... - π4/90 = ζ(4) = 1.082323...
- Khinchin–Lévy constant: 1.1865691104...http://mathworld.wolfram.com/Khinchin-LevyConstant.html
- √2s: 1.559610469...
- Favard constant: K1 = 1.57079633...
- log2 3: 1.584962501..., in fact, the logarithm of any positive integer to any integer base greater than one is either rational or transcendental.
- √2√2: 1.6325269...
- Komornik–Loreti constant: q = 1.787231650...
- Universal parabolic constantUniversal parabolic constantThe universal parabolic constant is a mathematical constant.It is defined as the ratio, for any parabola, of the arc length of the parabolic segment formed by the latus rectum to the focal parameter...
: P2 = 2.29558714939... - Gelfond–Schneider constant: 2.665144143...
- Euler's number: e = 2.718281828459045235360287471353...
- PiPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
: π = 3.141592653589793238462643383279... - Van der Pauw's constant: pi/ln(2) = 4.53236014182719380962...
- i√iImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
: 4.81047738..., √eπGelfond's constantIn mathematics, Gelfond's constant, named after Aleksandr Gelfond, is eπ, that is, e to the power of π. Like both e and π, this constant is a transcendental number. This can be proven by the Gelfond–Schneider theorem and noting the fact that... - TauTauTau is the 19th letter of the Greek alphabet. In the system of Greek numerals it has a value of 300.The name in English is pronounced , but in modern Greek it is...
, or 2π: τ = 6.283185307179586..., The ratio of the circumferenceCircumferenceThe circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
to a radiusRadiusIn classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
, and the number of radians in a complete circle - Gelfond's constantGelfond's constantIn mathematics, Gelfond's constant, named after Aleksandr Gelfond, is eπ, that is, e to the power of π. Like both e and π, this constant is a transcendental number. This can be proven by the Gelfond–Schneider theorem and noting the fact that...
: 23.14069263277925... - Ramanujan's constant: e(π√163) = 262537412640768743.99999999999925...
Suspected transcendentals
- -2W (½) = -0.703467422498391652049818601859902130..., the real solution to exp(x) = x2.
- Z(1)Riemann–Siegel formulaIn mathematics, the Riemann–Siegel formula is an asymptotic formula for the error of the approximate functional equation of the Riemann zeta function, an approximation of the zeta function by a sum of two finite Dirichlet series. It was found by in unpublished manuscripts of Bernhard Riemann...
: -0.736305462867317734677899828925614672... - Heath-Brown–Moroz constant: C = 0.001317641...
- Kepler–Bouwkamp constant: 0.1149420448...
- MRB constantMRB constantThe MRB constant, named after Marvin Ray Burns, is a mathematical constant for which no closed-form expression is known. It is not known whether the MRB constant is algebraic, transcendental, or even irrational....
: 0.187859... - Meissel–Mertens constant: M = 0.2614972128476427837554268386086958590516...
- Bernstein's constantBernstein's constantBernstein's constant, usually denoted by the Greek letter β , is a mathematical constant named after Sergei Natanovich Bernstein and is approximately equal to 0.2801694990.- Definition :...
: β = 0.2801694990... - Strongly carefree constant: 0.286747...
- Gauss–Kuzmin–Wirsing constant: λ1 = 0.3036630029...http://mathworld.wolfram.com/Gauss-Kuzmin-WirsingConstant.html
- Hafner–Sarnak–McCurley constant: 0.3532363719...
- Artin's constantArtin's conjecture on primitive rootsIn number theory, Artin's conjecture on primitive roots states that a given integer a which is not a perfect square and not −1 is a primitive root modulo infinitely many primes p. The conjecture also ascribes an asymptotic density to these primes...
: 0.3739558136... - Prime constantPrime constantThe prime constant is the real number \rho whose nth binary digit is 1 if n is prime and 0 if n is composite or 1.In other words, \rho is simply the number whose binary expansion corresponds to the indicator function of the set of prime numbers...
: ρ = 0.414682509851111660248109622... - Carefree constant: 0.428249...
- The LogarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of e to base 10: 0.434294481903251827651128918916605082294397005803... - S(1)Fresnel integral250px|thumb|S and C The maximum of C is about 0.977451424. If πt²/2 were used instead of t², then the image would be scaled vertically and horizontally ....
: 0.438259147390354766076756696625152... - F(1): 0.538079506912768419136387420407556...
- Stephens' constant: 0.575959...
- Euler–Mascheroni constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
: γ = 0.577215664901532860606512090082... - Golomb–Dickman constant: λ = 0.62432998854355087099293638310083724...
- Twin prime constant: C2 = 0.660161815846869573927812110014...
- Feller-Tornier constant: 0.661317...
- Laplace limitLaplace limitIn mathematics, the Laplace limit is the maximum value of the eccentricity for which the series solution to Kepler's equation converges. It is approximately...
: ε = 0.6627434193...http://mathworld.wolfram.com/LaplaceLimit.html - Taniguchi's constant: 0.678234...
- Continued Fraction Constant: C = 0.697774657964007982006790592551...
- Embree–Trefethen constant: β* = 0.70258...
- Sarnak's constant: 0.723648...
- Landau–Ramanujan constant: 0.76422365358922066299069873125...
- C(1)Fresnel integral250px|thumb|S and C The maximum of C is about 0.977451424. If πt²/2 were used instead of t², then the image would be scaled vertically and horizontally ....
: 0.77989340037682282947420641365... - ζ(3)−1 = 0.831907..., the probability that three random numbers have no common factor.
- Brun's constant for prime quadruplets: B2 = 0.8705883800...
- Quadratic class number constant: 0.881513...
- Catalan's constant: G = 0.915965594177219015054603514932384110774...
- Viswanath's constant: σ(1) = 1.13198824...
- ζ(3) = 1.202056903159594285399738161511449990764986292..., also known as Apéry's constantApéry's constantIn mathematics, Apéry's constant is a number that occurs in a variety of situations. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics...
, known to be irrational, but not known whether or not it is transcendentalTranscendental functionA transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
. - Vardi's constant: E = 1.264084735305...
- Glaisher–Kinkelin constant: A = 1.28242712...
- Mills' constant: A = 1.30637788386308069046...
- Totient summatory constant: 1.339784...
- Ramanujan–Soldner constant: μ = 1.451369234883381050283968485892027449493…
- Backhouse's constantBackhouse's constantBackhouse's constant is a mathematical constant founded by N. Backhouse and is approximately 1.456 074 948.It is defined by using the power series such that the coefficients of successive terms are the prime numbers:and whereThen:...
: 1.456074948... - Lieb's square ice constantLieb's square ice constantLieb's square ice constant is a mathematical constant used in the field of combinatorics. It was introduced by Elliott H. Lieb in 1967.-Definition:...
: 1.5396007... - Erdős–Borwein constant: E = 1.606695152415291763...
- Somos' quadratic recurrence constant: σ = 1.661687949633594121296...
- Niven's constantNiven's constantIn number theory, Niven's constant, named after Ivan Niven, is the largest exponent appearing in the prime factorization of any natural number n "on average"...
: c = 1.705211... - Brun's constant: B2 = 1.902160583104...
- Landau's totient constant: 1.943596...
- exp(-W 0(-ln(3⅓))) = 2.47805268028830..., the smaller solution to 3x = x3 and what, when put to the root of itself, is equal to 3 put to the root of itself.
- Second Feigenbaum constant: α = 2.5029...
- Sierpiński's constant: K = 2.5849817595792532170658936...
- Barban's constant: 2.596536...
- Khinchin's constant: K0 = 2.685452001...http://mathworld.wolfram.com/KhinchinsConstant.html
- Fransén–Robinson constant: F = 2.8077702420...
- Murata's constant: 2.826419...
- Lévy's constantLévy's constantIn mathematics Lévy's constant occurs in an expression for the asymptotic behaviour of the denominators of the convergents of continued fractions....
: γ = 3.275822918721811159787681882... - Reciprocal Fibonacci constant: ψ = 3.359885666243177553172011302918927179688905133731...
- First Feigenbaum constant: δ = 4.6692...
Numbers not known with high precision
- Landau's constantLandau's constantsIn complex analysis, a branch of mathematics, Landau's constants are certain mathematical constants that describe the behaviour of holomorphic functions defined on the unit disk...
: 0.4330 < B < 0.472 - Bloch's constant: 0.4332 < B < 0.4719
- Landau's constantLandau's constantsIn complex analysis, a branch of mathematics, Landau's constants are certain mathematical constants that describe the behaviour of holomorphic functions defined on the unit disk...
: 0.5 < L < 0.544 - Landau's constantLandau's constantsIn complex analysis, a branch of mathematics, Landau's constants are certain mathematical constants that describe the behaviour of holomorphic functions defined on the unit disk...
: 0.5 < A < 0.7853 - Grothendieck constant: 1.67 < k < 1.79
Algebraic complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s
- Imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
:
- nth roots of unity:
Other hypercomplex numbers
- The quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s - The octonionOctonionIn mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s - The sedenionSedenionIn abstract algebra, sedenions form a 16-dimensional non-associative algebra over the reals obtained by applying the Cayley–Dickson construction to the octonions...
s - The dual numberDual numberIn linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...
s (with an infinitesimalInfinitesimalInfinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
)
Transfinite numberTransfinite numberTransfinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers, yet not necessarily absolutely infinite. The term transfinite was coined by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these...
s
- InfinityInfinityInfinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
in general:
- Aleph-null:

- Aleph-one:
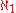
- Beth-one: (
 ) is the cardinality of the continuumCardinality of the continuumIn set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
) is the cardinality of the continuumCardinality of the continuumIn set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
:
Numbers representing measured quantities
- Pair: 2 (the base of the binary numeral systemBinary numeral systemThe binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
) - DozenDozenA dozen is a grouping of approximately twelve. The dozen may be one of the earliest primitive groupings, perhaps because there are approximately a dozen cycles of the moon or months in a cycle of the sun or year...
: 12 (the base of the duodecimalDuodecimalThe duodecimal system is a positional notation numeral system using twelve as its base. In this system, the number ten may be written as 'A', 'T' or 'X', and the number eleven as 'B' or 'E'...
numeral system) - Baker's dozen: 13
- Score20 (number)20 is the natural number following 19 and preceding 21. A group of twenty units may also be referred to as a score.-In mathematics:*20 is the basis for vigesimal number systems....
: 20 (the base of the vigesimalVigesimalThe vigesimal or base 20 numeral system is based on twenty .- Places :...
numeral system) - GrossGross (unit)A gross is equal to a dozen dozen, i.e. 12 × 12 = 144.It can be used in duodecimal counting. The use of gross likely originated from the fact that 144 can be counted on the fingers using the fingertips and first two joints of each finger when marked by the thumb of one hand. The other hand...
: 144 (= 122) - Great gross: 1728 (= 123)
Numbers representing scientific quantities
- Avogadro constant: N = 6.0221417930... mol−1
- ElectronvoltElectronvoltIn physics, the electron volt is a unit of energy equal to approximately joule . By definition, it is equal to the amount of kinetic energy gained by a single unbound electron when it accelerates through an electric potential difference of one volt...
: eV = 1.60217648740... J - Electron relative atomic mass: A(e) = 0.0005485799094323...
- Fine structure constant: α = 0.007297352537650...
- Molar mass constantMolar mass constantThe molar mass constant, symbol Mu, is a physical constant which relates atomic weight and molar mass. Its value is defined to be 1 g/mol in SI units....
: M = 0.001 kg/mol - Planck constantPlanck constantThe Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
: h = 6.6260689633... Js - Rydberg constantRydberg constantThe Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
: R = 10973731.56852773... m−1 - Speed of light in vacuumSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
: c = 299792458 m/s - Stefan-Boltzmann constantStefan-Boltzmann constantThe Stefan–Boltzmann constant , a physical constant denoted by the Greek letter σ, is the constant of proportionality in the Stefan–Boltzmann law: the total energy radiated per unit surface area of a black body in unit time is proportional to the fourth power of the thermodynamic temperature.The...
: σ = 5.670400 W • m−2 • K−4
Further reading
- Kingdom of Infinite Number: A Field Guide by Bryan Bunch, W.H. Freeman & Company, 2001. ISBN 0-7167-4447-3
External links
- The Database of Number Correlations: 1 to 2000+
- What's Special About This Number? A Zoology of Numbers: from 0 to 500
- See how to write big numbers
- The MegaPenny Project – Visualizing big numbers
- About big numbers
- Robert P. Munafo's Large Numbers page
- Different notations for big numbers – by Susan Stepney
- Names for Large Numbers, in How Many? A Dictionary of Units of Measurement by Russ Rowlett
- What's Special About This Number? (from 0 to 9999)

