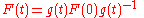Riemannian connection on a surface
Encyclopedia
In mathematics
, the Riemannian connection on a surface
or Riemannian 2-manifold
refers to several intrinsic geometric structures discovered by Tullio Levi-Civita
, Élie Cartan
and Hermann Weyl
in the early part of the twentieth century: parallel transport
, covariant derivative
and connection form
. These concepts were put in their final form using the language of principal bundle
s only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces
, due in large part to Carl Friedrich Gauss
, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame
as well as the Riemannian geometry
of higher dimensional Riemannian manifold
s. This account is intended as an introduction to the theory of connections
.
After the classical work of Gauss on the differential geometry of surfaces
and the subsequent emergence of the concept of Riemannian manifold
initiated by Bernhard Riemann
in the mid-nineteenth century, the geometric notion of connection
developed by Tullio Levi-Civita
, Élie Cartan
and Hermann Weyl
in the early twentieth century represented a major advance in differential geometry. The introduction of parallel transport
, covariant derivative
s and connection form
s gave a more conceptual and uniform way of understanding curvature, which not only allowed generalisations to higher dimensional manifolds but also provided an important tool for defining new geometric invariants, called characteristic classes. The approach using covariant derivatives and connections is nowadays the one adopted in more advanced textbooks.
Although Gauss was the first to study the differential geometry of surfaces in E3, it was not until Riemann's Habilitationsschrift of 1854 that the notion of a Riemannian space was introduced. Christoffel introduced his eponymous symbols in 1869. Tensor calculus was developed by Ricci
, who published a systematic treatment with Levi-Civita in 1901. Covariant differentiation of tensors was given a geometric interpretation by who introduced the notion of parallel transport on surfaces. His discovery prompted Weyl and Cartan
to introduce various notions of connection, including in particular that of affine connection. Cartan's approach was rephrased in the modern language of principal bundles by Ehresmann
, after which the subject rapidly took its current form following contributions by Chern, Ambrose and Singer, Kobayashi, Nomizu, Lichnerowicz and others.
Connections on a surface can be defined in a variety of ways. The Riemannian connection or Levi-Civita connection
is perhaps most easily understood in terms of lifting vector field
s, considered as first order differential operator
s acting on functions on the manifold, to differential operators on the frame bundle
: in the case of an embedded surface, the lift is very simply described in terms of orthogonal projection. Indeed the vector bundles associated with the frame bundle are all sub-bundles of trivial bundles that extend to the ambient Euclidean space; a first order differential operator can always be applied to a section of a trivial bundle, in particular to a section of the original sub-bundle, although the resulting section might no longer be a section of the sub-bundle. This can be corrected by projecting orthogonally.
The Riemannian connection can also be characterized abstractly independently of an embedding. The equations of geodesics are easy to write in terms of the Riemannian connection, which can be locally expressed in terms of the Christoffel symbols. Along a curve in the surface, the connection defines a first order differential equation in the frame bundle. The monodromy
of this equation defines parallel transport
for the connection, a notion introduced in this context by Levi-Civita. This gives an equivalent more geometric way of describing the connection in terms of lifting paths in the manifold to paths in the frame bundle. This formalised the classical theory of the "moving frame", favoured by French authors. Lifts of loops about a point give rise to the holonomy group at that point. The Gaussian curvature at a point can be recovered from parallel transport around increasingly small loops at the point. Equivalently curvature can be calculated directly infinitesimally in terms of Lie bracket
s of lifted vector fields.
The approach of Cartan, using connection 1-forms on the frame bundle
of M, gives a third way to understand the Riemannian connection, which is particularly easy to describe for an embedded surface. Thanks to a result of , later generalized by , the Riemannian connection on a surface embedded in Euclidean space E3 is just the pullback under the Gauss map of the Riemannian connection on S2.
Using the identification of S2 with the homogeneous space
SO(3)/SO(2), the connection 1-form is just a component of the Maurer-Cartan 1-form
on SO(3). In other words everything reduces to understanding the 2-sphere properly.
For a surface M embedded in E3 (or more generally a higher dimensional Euclidean space), there are several equivalent definitions of a vector field
X on M:
The last condition means that the assignment f Xf on C∞(M) satisfies the Leibniz rule
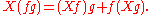
The space of all vector field
s
(M) forms a module
over C∞(M), closed under the Lie bracket
with a C∞(M)-valued inner product (X,Y), which encodes the Riemannian metric on M.
Since
(M) is a submodule of C∞(M, E3)=C∞(M)
E3, the operator X
I is defined on 
(M), taking values in C∞(M, E3).
Let P be the smooth map from M into M3(R) such that P(p) is the orthogonal projection of E3 onto the tangent space at p.
Pointwise multiplication by P gives a C∞(M)-module map of C∞(M, E3) onto
(M) . The assignment
defines an operator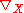
on 
(M) called the covariant derivative, satisfying the following properties
The first three properties state that
is an affine connection
compatible with the metric, sometimes also called a hermitian or metric connection
. The last symmetry property says that the torsion tensor
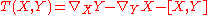
vanishes identically, so that the affine connection is torsion-free.
Although the Riemannian connection was defined using an embedding in Euclidean space, this uniqueness property means that it is in fact an intrinsic invariant of the surface.
It existence can be proved directly for a general surface by noting that the four properties imply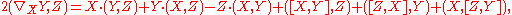
so that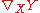
depends only on the metric and is unique. On the other hand if this is used as a definition of 
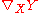, it is readily checked that the four properties above are satisfied.
Equivalently, in local coordinates (x,y) with basis tangent vectors e1=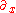
and e2 =
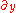, the connection 
can be expressed purely in terms of the metric using the Christoffel symbols
:
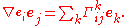
If c(t) is a path in M, then the Euler equations for c to be a geodesic can be written more compactly as
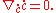
Given a curve in the Euclidean plane and a vector at the starting point, the vector can be transported along the curve by requiring the moving vector to remain parallel to the original one and of the same length, i.e. it should remain constant along the curve. If the curve is closed, the vector will be unchanged when the starting point is reached again. This is well known not to be possible on a general surface, the sphere being the most familiar case. In fact it is not usually possible to identify simultaneously or "parallelize" all the tangent planes of such a surface: the only parallelizable closed surfaces are those homeomorphic to a torus.
Parallel transport can always be defined along curves on a surface using only the metric on the surface. Thus tangent planes along a curve can be identified using the intrinsic geometry, even when the surface itself is not parallelizable.
Parallel transport along geodesics, the "straight lines" of the surface, is easy to define. A vector in the tangent plane is transported along a geodesic as the unique vector field with constant length and making a
constant angle with the velocity vector of the geodesic.
For a general curve, its geodesic curvature measures how far the curve departs from being a geodesics; it is defined as the rate at which the curve's velocity vector rotates in the surface. In turn the geodesic curvature determines how vectors in the tangent planes along the curve should rotate during parallel transport.
A vector field v(t) along a unit speed curve c(t), with geodesic curvature kg(t), is said to be parallel along the curve if
|
|}
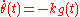
This yields the previous rule for parallel transport along a geodesic, because in that case kg = 0, so the angle θ(t) should remain constant. The existence of parallel transport follows from standard existence theorems for ordinary differential equation
s. The above differential equation can be rewritten in terms of the covariant derivative as
|
|}
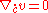
This equation shows once more that parallel transport depends only on the metric structure so is an intrinsic invariant of the surface. Parallel transport can be extended immediately to piecewise C1 curves.
When M is a surface embedded in E3, this last condition can be written in terms of the projection-valued function P as
|
|}
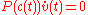
or in other words:
Arnold
has suggested that since parallel transport on a geodesic segment is easy to describe, parallel transport on an arbitrary C1 curve could be constructed as a limit of parallel transport on an approximating family of piecewise geodesic curves.
This equation shows once more that parallel transport depends only on the metric structure so is an intrinsic invariant of the surface; it is another way of writing the ordinary differential equation involving the geodesic curvature of c. Parallel transport can be extended immediately to piecewise C1 curves.
The covariant derivative can in turn be recovered from parallel transport. In fact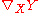
can be calculated at a point p, by taking a curve c through p with tangent X, using parallel transport to view the restriction of Y to c as a function in the tangent space at p and then taking the derivative.
on the surface means that an "outward pointing" normal unit vector n is defined at each point of the surface and hence a determinant can be defined on tangent vectors v and w at that point:
using the usual scalar triple product on E3 (itself a determinant).
An ordered basis or frame v, w in the tangent space is said to be oriented if det(v, w) is positive.
Since the group of rotations in the plane SO(2) acts simply transitively on oriented orthonormal frames in the plane, it follows that it also acts on the frame or circle bundles of M. The definitions of the tangent bundle
, the unit tangent bundle and the (oriented orthonormal) frame bundle
E can be extended to arbitrary surfaces in the usual way. There is a similar identification between the latter two which again become principal SO(2)-bundles. In other words:
There is also a corresponding notion of parallel transport in the setting of frame bundles:
This statement means that any frame on a curve can be parallelly transported along the curve. This is precisely the idea of "moving frames".
Since any unit tangent vector can be completed uniquely to an oriented frame, parallel transport of tangent vectors implies (and is equivalent to) parallel transport of frames. The lift of a geodesic in M turns out to be a geodesic in E for the Sasaki metric (see below). Moreover the Gauss map of M into S2 induces a natural map between the associated frame bundles which is equivariant
for the actions of SO(2).
Cartan's idea of introducing the frame bundle as a central object was the natural culmination of the theory of moving frame
s, developed in France by Darboux and Goursat. It also echoed parallel developments in Albert Einstein
's theory of relativity
. Objects appearing in the formulas of Gauss, such as the Christoffel symbols, can be given a natural geometric interpretation in this framework. Unlike the more intuitive normal bundle
, easily visualised as a tubular neighbourhood of an embedded surface in E3, the frame bundle is an intrinsic invariant that can be defined independently of an embedding. When there is an embedding, it can also be visualised as a subbundle of the Euclidean frame bundle E3 x SO(3), itself a submanifold
of E3 x M3(R).
The theory of connections according to Élie Cartan
, and later Charles Ehresmann
, revolves around:
All "natural" vector bundle
s associated with the manifold M, such as the tangent bundle
, the cotangent bundle
or the exterior bundle
s, can be constructed from the frame bundle using the representation theory of the structure group K = SO(2), a compact matrix group.
Cartan's definition of a connection can be understood as a way of lifting vector fields on M to vector fields on the frame bundle E invariant under the action of the structure group K. Since parallel transport has been defined as a way of lifting piecewise C1 paths from
M to E, this automatically induces infinitesimally a way to lift vector fields or tangent vectors from M to E. At a point take a path with given tangent vector and then map it to the tangent vector of the lifted path. (For vector fields the curves can be taken to be the integral curves of a local flow.) In this way any vector field X on M can be lifted to a vector field X* on E satisfying
Here K acts as a periodic flow on E, so the canonical generator A of its Lie algebra acts as the corresponding vector field, called the vertical vector field A*. It follows from the above conditions that, in the tangent space of an arbitrary point in E, the lifts X* span a two-dimensional subspace of horizontal vectors, forming a complementary subspace to the vertical vectors. The canonical Riemannian metric on E of Shigeo Sasaki is defined by making the horizontal and vertical subspaces orthogonal, giving each subspace its natural inner product.
Horizontal vector fields admit the following characterisation:
This "universal lift" then immediately induces lifts to vector bundles associated with E and hence allows the covariant derivative, and its generalisation to forms, to be recovered.
If σ is a representation of K on a finite-dimensional vector space V, then the associated vector bundle E XK V over M has a C∞(M)-module of sections that can be identified with
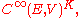
the space of all smooth functions ξ : E → V which are K-equivariant in the sense that
for all x ∈ E and g ∈ K.
The identity representation of SO(2) on R2 corresponds to the tangent bundle of M.
The covariant derivative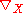
is defined on an invariant section ξ by the formula
The connection on the frame bundle can also be described using K-invariant differential 1-forms on E.
The frame bundle E is a 3-manifold
. The space of p-forms
on E is denoted Λp(E). It admits a natural action of the structure group K.
Given a connection on the principal bundle E corresponding to a lift X X* of vector fields on M, there is a unique connection form
ω in
,
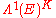the space of K-invariant 1-forms on E, such that
for all vector fields X on M and
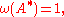
for the vector field A* on E corresponding to the canonical generator A of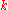
.
Conversely the lift X* is uniquely characterised by the following properties:
If π: E
M is the nature projection, the 1-forms θ1 and θ2 are defined by
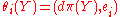
where Y is a vector field on E and e1, e2 are the tangent vectors to M of the orthonormal frame.
These 1-forms satisfy the following structural equations, due in this formulation to Cartan:
(First structural equations)
(Second structural equation)
where K is the Gaussian curvature on M.
This geometric interpretation of curvature relies on a similar geometric of the Lie bracket
of two vector field
s on E. Let U1 and U2 be vector fields on E with corresponding local flows
αt and βt.
In general the end point E will differ from the starting point A. As s
0, the end point E will trace out a curve through A. The Lie bracket [U1,U2] at x is precisely the tangent vector to this curve at A.
To apply this theory, introduce vector fields U1, U2 and V on the frame bundle E which are dual to the 1-forms
θ1, θ2 and ω at each point. Thus
Moreover V is invariant under K and U1, U2 transform according to the identity representation of K.
The structural equations of Cartan imply the following Lie bracket relations:
The geometrical interpretation of the Lie bracket can be applied to the last of these equations. Since ω(Ui)=0, the flows αt and βt in E are lifts by parallel transport of their projections in M.
Informally the idea is as follows. The starting point A and end point E essentially differ by an element of SO(2), that is an angle of rotation. The area enclosed by the projected path in M is approximately
. So in the limit as s 
0, the angle of rotation divided by this area tends to the coefficient of V, i.e. the curvature.
This reasoning is made precise in the following result.
In symbols, the holonomy angle mod 2π is given by
where the integral is with respect to the area form on M.
This result implies the relation between Gaussian curvature because as the triangle shrinks in size to a point, the ratio of this angle to the area tends to the Gaussian curvature at the point. The result can be proved by a combination of Stokes's theorem and Cartan's structural equations and can in turn be used to obtain a generalisation of Gauss's theorem on geodesics triangles to more general triangles.
One of the other standard approaches to curvature, through the covariant derivative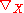
, identifies the difference
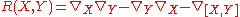
as a field of endomorphisms of the tangent bundle, the Riemann curvature tensor
.
Since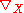
is induced by the lifted vector field X* on E, the use of the vector fields Ui and V and their Lie brackets is more or less equivalent to this approach. The vertical vector field W=A* corresponding to the canonical generator A of 
could also be added since it commutes with V and satisfies [W,U1] = U2 and [W,U2] = —U1.
S2 can be identified with the unit sphere in E3
Its tangent bundle T, unit tangent bundle U and oriented orthonormal frame bundle E are given by
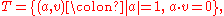
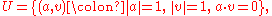
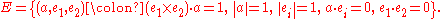
The map sending (a,v) to (a, v, a x v) allows U and E to be identified.
Let
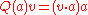
be the orthogonal projection onto the normal vector at a, so that
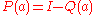
is the orthogonal projection onto the tangent space at a.
The group G = SO(3) acts by rotation on E3 leaving S2 invariant. The stabilizer subgroup K of the vector (1,0,0) in E3 may be identified with SO(2) and hence
This action extends to an action on T, U and E by making G act on each component. G acts transitively on S2 and simply transitively on U and E.
The action of SO(3) on E commutes with the action of SO(2) on E that rotates frames
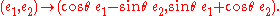
Thus E becomes a principal bundle with structure group K. Taking the G-orbit of the point ((1,0,0),(0,1,0),(0,0,1)), the space E may be identified with G. Under this identification the actions of G and K on E become left and right translation. In other words:
The Lie algebra
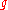of SO(3) consists of all skew-symmetric
real 3 x 3 matrices. the adjoint action of G by conjugation on
reproduces the action of G on E3. The group SU(2) has a 3-dimensional Lie algebra consisting of complex skew-hermitian
traceless 2 x 2 matrices, which is isomorphic to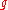
. The adjoint action of SU(2) factors through its centre, the matrices ± I. Under these identifications, SU(2) is exhibited as a double cover of SO(3), so that SO(3) = SU(2) / ± I. On the other hand SU(2) is diffeomorphic to the 3-sphere and under this identification the standard Riemannian metric on the 3-sphere becomes the essentially unique biinvariant Riemannian metric on SU(2). Under the quotient by ± I, SO(3) can be identified with the real projective space
of dimension 3 and itself has an essentially unique biinvariant Riemannian metric. The geometric exponential map for this metric at I coincides with the usual exponential function on matrices and thus the geodesics through I are have the form exp Xt where X is a skew-symmetric matrix.
In this case the Sasaki metric agrees with this biinvariant metric on SO(3).
The actions of G on itself, and hence on C∞(G) by left and right translation induce infinitesimal actions of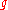
on C∞(G) by vector fields
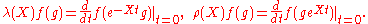
The right and left invariant vector fields are related by the formula
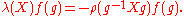
The vector fields λ(X) and ρ(X) commute with right and left translation and give all right and left invariant vector fields on G. Since
C∞(S2) = C∞(G/K) can be identified with C∞(G)K, the function invariant under right translation by K, the operators λ(X) also induces vector fields Π(X) on S2.
Let A, B, C be the standard basis of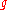
given by
Their Lie bracket
s [X,Y] = XY – YX are given by
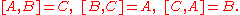
The vector fields λ(A), λ(B), λ(C) form a basis of the tangent space at each point of G.
Similarly the left invariant vector fields ρ(A), ρ(B), ρ(C) form a basis of the tangent space at each point of G.
Let α, β, γ be the corresponding dual basis of left invariant 1-forms on G. The Lie bracket relations imply the Maurer-Cartan equations
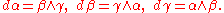
These are also the corresponding components of the Maurer-Cartan form
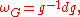
a left invariant matrix-valued 1-form on G, which satisfies the relation
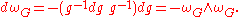
The inner product on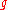
defined by
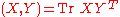
is invariant under the adjoint action. Let π be the orthogonal projection onto the subspace generated by A, i.e. onto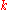
, the Lie algebra of K. For X in 
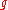, the lift of the vector field Π(X) from C∞(G/K) to C∞(G) is given by the formula
This lift is G-equivariant on vector fields of the form Π(X) and has a unique extension to more general vector fields on G / K.
The left invariant 1-form α is the connection form ω on G corresponding to this lift. The other two 1-forms in the Cartan structural equations are given by θ1 = β and θ2 = γ. The structural equations themselves are just the Maurer-Cartan equations. In other words;
Since α is the connection form,
The existence of the basis vector fields λ(A), λ(B), λ(C) shows that SO(3) is parallelizable. This is not true for SO(3)/SO(2) by the hairy ball theorem
: S2 does not admit any nowhere vanishing vector fields.
Parallel transport in the frame bundle amounts to lifting a path from SO(3)/SO(2) to SO(3). It can be accomplished by directly solving a matrix-valued ordinary differential equation ("transport equation") of the form gt = A · g where A(t) is skew-symmetric and g takes values in SO(3).
In fact it is equivalent and more convenient to lift a path from SO(3)/O(2) to SO(3). Note that O(2) is the normaliser of SO(2) in SO(3) and the quotient group O(2)/SO(2), the so called the Weyl group
, is a group of order 2 which acts on SO(3)/SO(2) = S2 as the antipodal map. The quotient SO(3)/O(2) is the real projective plane
. It can be identified with space of rank one or rank two projections Q in M3(R). Taking Q to be a rank 2 projection and setting F = 2Q − I, a model of the surface SO(3)/O(2) is given by
matrices F satisfying F2 = I, F = FT and Tr F = 1. Taking F0= diag (–1,1,1) as base point, every F can be written in the form g F0 g−1.
If Q(t) is the corresponding path of rank 2 projections, the conditions for parallel transport are
Set A = ½Ft F. Since F2 = I and F is symmetric, A is skew-symmetric and satisfies
QAQ = 0.
The unique solution g(t) of the ordinary differential equation
with initial condition g(0) = I guaranteed by the Picard–Lindelöf theorem
, must have gTg constant and therefore I, since
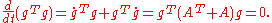
Moreover
since g−1Fg has derivative 0:
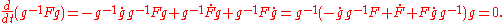
Hence Q = g Q0 g−1. The condition QAQ=0 implies Q gt g−1 Q = 0 and hence that Q0 g−1 gt Q0 =0.
There is another kinematic way of understanding parallel transport and geodesic curvature in terms of "rolling without slipping or twisting". Although well known to differential geometers since the early part of the twentieth century, it has also been applied to problems in engineering
and robotics
. Consider the 2-sphere as a rigid body in three dimensional space rolling without slipping or twisting on a horizontal plane. The point of contact will describe a curve in the plane and on the surface. At each point of contact the different tangent planes of the sphere can be identified with the horizontal plane itself and hence with one another.
This is particularly easy to visualize for a sphere: it is exactly the way a marble can be rolled along a perfectly flat table top.
The roles of the plane and the sphere can be reversed to provide an alternative but equivalent point of view. The sphere is regarded as fixed and the plane has to roll without slipping or twisting along the given curve on the sphere.
S2 extends to a SO(2)-equivariant map between the orthonormal frame bundles E 
SO(3). Indeed the triad consisting of the tangent frame and the normal vector gives an element of SO(3).
In 1956 Kobayashi proved that:
This means that the forms ω, θ1 and θ2 on E are obtained by pulling back those on SO(3); and that lifting paths from M to E can be accomplished by mapping the path to the 2-sphere, lifting the path to SO(3) and then pulling back the lift to E. Thus for embedded surfaces, the 2-sphere with the principal connection on its frame bundle provides a "universal model", the prototype for the universal bundles discussed in .
In more concrete terms this allows parallel transport to be described explicitly using the transport equation. Parallel transport along a curve c(t), with t taking values in [0,1], starting from a tangent from a tangent vector v0 also amounts to finding a map v(t) from [0,1] to R3 such that
This always has a unique solution, called the parallel transport of v0 along c.
The existence of parallel transport can be deduced using the analytic method described for SO(3)/SO(2), which from a path into the rank two projections
Q(t) starting at Q0 produced a path g(t) in SO(3) starting at I such that
g(t) is the unique solution of the transport equation
with g(0) = I and F = 2Q − I. Applying this with Q(t) = P(c(t)), it follows that, given a tangent vector v0 in the tangent space to M at c(0),
the vector v(t)=g(t)v0 lies in the tangent space to M at c(t) and satisfies the equation
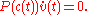
It therefore is exactly the parallel transport of v along the curve c. In this case the length of the vector v(t) is constant. More generally if another initial tangent vector u0 is taken instead of v0, the inner product (v(t),u(t)) is constant. The tangent spaces along the curve c(t) are thus canonically identified as inner product spaces by parallel transport so that parallel transport gives an isometry between the tangent planes. The condition on the velocity vector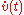
may be rewritten in terms of the covariant derivative as
the defining equation for parallel transport.
The kinematic way of understanding parallel transport for the sphere applies equally well to any closed surface in E3 regarded as a rigid body in three dimensional space rolling without slipping or twisting on a horizontal plane. The point of contact will describe a curve in the plane and on the surface. As for the sphere, the usual curvature
of the planar curve equals the geodesic curvature of the curve traced on the surface.
This geometric way of viewing parallel transport can also be directly expressed in the language of geometry. The envelope
of the tangent planes to M along a curve c is a surface with vanishing Gaussian curvature, which by Minding's theorem, must be locally isometric to the Euclidean plane. This identification allows parallel transport to be defined, because in the Euclidean plane all tangent planes are identified with the space itself.
There is another simple way of constructing the connection form ω using the embedding of M in E3.
The tangent vectors e1 and e2 of a frame on M define smooth functions from E with values in R3, so each gives a 3-vector of functions and in particular de1 is a 3-vector of 1-forms on E.
The connection form is given by
taking the usual scalar product on 3-vectors.
ω is the pullback
of one of the three right invariant Maurer-Cartan form
s on SO(3). The 1-forms ψ and χ are defined to be the pullbacks of the other two.
These 1-forms satisfy the following structure equations:
(symmetry equation)
(Gauss equation)
(Codazzi equations)
The Gauss–Codazzi equations
for χ, ψ and ω follow immediately from the Maurer-Cartan equations for the three right invariant 1-forms on SO(3).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Riemannian connection on a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
or Riemannian 2-manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
refers to several intrinsic geometric structures discovered by Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
, Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
and Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
in the early part of the twentieth century: parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
, covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
and connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
. These concepts were put in their final form using the language of principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces
Differential geometry of surfaces
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....
, due in large part to Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame
Moving frame
In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
as well as the Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
of higher dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s. This account is intended as an introduction to the theory of connections
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
.
Historical overview
Differential geometry of surfaces
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....
and the subsequent emergence of the concept of Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
initiated by Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
in the mid-nineteenth century, the geometric notion of connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
developed by Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
, Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
and Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
in the early twentieth century represented a major advance in differential geometry. The introduction of parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
, covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
s and connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
s gave a more conceptual and uniform way of understanding curvature, which not only allowed generalisations to higher dimensional manifolds but also provided an important tool for defining new geometric invariants, called characteristic classes. The approach using covariant derivatives and connections is nowadays the one adopted in more advanced textbooks.
Although Gauss was the first to study the differential geometry of surfaces in E3, it was not until Riemann's Habilitationsschrift of 1854 that the notion of a Riemannian space was introduced. Christoffel introduced his eponymous symbols in 1869. Tensor calculus was developed by Ricci
Ricci
Ricci is an Italian surname, and can also be a shortened version of Riccardo, as a first name and may refer to:-Surname:* Christie Ricci, American wrestler* Christina Ricci, American actress* Fausto Ricci, Italian motorcycle racer...
, who published a systematic treatment with Levi-Civita in 1901. Covariant differentiation of tensors was given a geometric interpretation by who introduced the notion of parallel transport on surfaces. His discovery prompted Weyl and Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
to introduce various notions of connection, including in particular that of affine connection. Cartan's approach was rephrased in the modern language of principal bundles by Ehresmann
Charles Ehresmann
Charles Ehresmann was a French mathematician who worked on differential topology and category theory. He is known for work on the topology of Lie groups, the jet concept , and his seminar on category theory.He attended the École Normale Supérieure in Paris before performing one year of military...
, after which the subject rapidly took its current form following contributions by Chern, Ambrose and Singer, Kobayashi, Nomizu, Lichnerowicz and others.
Connections on a surface can be defined in a variety of ways. The Riemannian connection or Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
is perhaps most easily understood in terms of lifting vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s, considered as first order differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s acting on functions on the manifold, to differential operators on the frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
: in the case of an embedded surface, the lift is very simply described in terms of orthogonal projection. Indeed the vector bundles associated with the frame bundle are all sub-bundles of trivial bundles that extend to the ambient Euclidean space; a first order differential operator can always be applied to a section of a trivial bundle, in particular to a section of the original sub-bundle, although the resulting section might no longer be a section of the sub-bundle. This can be corrected by projecting orthogonally.
The Riemannian connection can also be characterized abstractly independently of an embedding. The equations of geodesics are easy to write in terms of the Riemannian connection, which can be locally expressed in terms of the Christoffel symbols. Along a curve in the surface, the connection defines a first order differential equation in the frame bundle. The monodromy
Monodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
of this equation defines parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
for the connection, a notion introduced in this context by Levi-Civita. This gives an equivalent more geometric way of describing the connection in terms of lifting paths in the manifold to paths in the frame bundle. This formalised the classical theory of the "moving frame", favoured by French authors. Lifts of loops about a point give rise to the holonomy group at that point. The Gaussian curvature at a point can be recovered from parallel transport around increasingly small loops at the point. Equivalently curvature can be calculated directly infinitesimally in terms of Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
s of lifted vector fields.
The approach of Cartan, using connection 1-forms on the frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
of M, gives a third way to understand the Riemannian connection, which is particularly easy to describe for an embedded surface. Thanks to a result of , later generalized by , the Riemannian connection on a surface embedded in Euclidean space E3 is just the pullback under the Gauss map of the Riemannian connection on S2.
Using the identification of S2 with the homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
SO(3)/SO(2), the connection 1-form is just a component of the Maurer-Cartan 1-form
Maurer-Cartan form
In mathematics, the Maurer–Cartan form for a Lie group G is a distinguished differential one-form on G that carries the basic infinitesimal information about the structure of G...
on SO(3). In other words everything reduces to understanding the 2-sphere properly.
Covariant derivative
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
X on M:
- a smooth map of M into E3 taking values in the tangent space at each point;
- the velocity vectorVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of a local flowFlow (mathematics)In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
on M; - a first order differential operatorDifferential operatorIn mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
without constant term in any local chart on M; - a derivationDerivationDerivation may refer to:* Derivation , a function on an algebra which generalizes certain features of the derivative operator* Derivation * Derivation in differential algebra, a unary function satisfying the Leibniz product law...
of C∞(M).
The last condition means that the assignment f Xf on C∞(M) satisfies the Leibniz rule
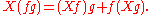
The space of all vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s
(M) forms a moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over C∞(M), closed under the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
with a C∞(M)-valued inner product (X,Y), which encodes the Riemannian metric on M.
Since
(M) is a submodule of C∞(M, E3)=C∞(M) E3, the operator X I is defined on (M), taking values in C∞(M, E3).Let P be the smooth map from M into M3(R) such that P(p) is the orthogonal projection of E3 onto the tangent space at p.
Pointwise multiplication by P gives a C∞(M)-module map of C∞(M, E3) onto
(M) . The assignment |
defines an operator
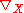on (M) called the covariant derivative, satisfying the following properties-
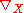is C∞(M)-linear in X -
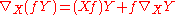(Leibniz rule for derivation of a module) -
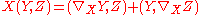(compatibility with the metric) -
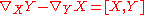(symmetry property).
The first three properties state that
is an affine connectionAffine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
compatible with the metric, sometimes also called a hermitian or metric connection
Metric connection
In mathematics, a metric connection is a connection in a vector bundle E equipped with a metric for which the inner product of any two vectors will remain the same when those vectors are parallel transported along any curve...
. The last symmetry property says that the torsion tensor
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
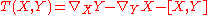
vanishes identically, so that the affine connection is torsion-free.
Although the Riemannian connection was defined using an embedding in Euclidean space, this uniqueness property means that it is in fact an intrinsic invariant of the surface.
It existence can be proved directly for a general surface by noting that the four properties imply
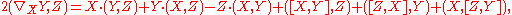
so that
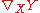depends only on the metric and is unique. On the other hand if this is used as a definition of 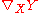, it is readily checked that the four properties above are satisfied.Equivalently, in local coordinates (x,y) with basis tangent vectors e1=
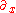and e2 =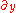, the connection can be expressed purely in terms of the metric using the Christoffel symbolsChristoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
:
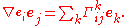
If c(t) is a path in M, then the Euler equations for c to be a geodesic can be written more compactly as
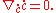
Parallel transport
Parallel transport can always be defined along curves on a surface using only the metric on the surface. Thus tangent planes along a curve can be identified using the intrinsic geometry, even when the surface itself is not parallelizable.
Parallel transport along geodesics, the "straight lines" of the surface, is easy to define. A vector in the tangent plane is transported along a geodesic as the unique vector field with constant length and making a
constant angle with the velocity vector of the geodesic.
For a general curve, its geodesic curvature measures how far the curve departs from being a geodesics; it is defined as the rate at which the curve's velocity vector rotates in the surface. In turn the geodesic curvature determines how vectors in the tangent planes along the curve should rotate during parallel transport.
A vector field v(t) along a unit speed curve c(t), with geodesic curvature kg(t), is said to be parallel along the curve if
- it has constant length
- the angle θ(t) that it makes with the velocity vector
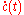satisfies
-
- {| border="1" cellspacing="0" cellpadding="5"
|
|}
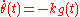
This yields the previous rule for parallel transport along a geodesic, because in that case kg = 0, so the angle θ(t) should remain constant. The existence of parallel transport follows from standard existence theorems for ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s. The above differential equation can be rewritten in terms of the covariant derivative as
-
- {| border="1" cellspacing="0" cellpadding="5"
|
|}
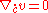
This equation shows once more that parallel transport depends only on the metric structure so is an intrinsic invariant of the surface. Parallel transport can be extended immediately to piecewise C1 curves.
When M is a surface embedded in E3, this last condition can be written in terms of the projection-valued function P as
-
- {| border="1" cellspacing="0" cellpadding="5"
|
|}
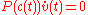
or in other words:
Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
has suggested that since parallel transport on a geodesic segment is easy to describe, parallel transport on an arbitrary C1 curve could be constructed as a limit of parallel transport on an approximating family of piecewise geodesic curves.
This equation shows once more that parallel transport depends only on the metric structure so is an intrinsic invariant of the surface; it is another way of writing the ordinary differential equation involving the geodesic curvature of c. Parallel transport can be extended immediately to piecewise C1 curves.
The covariant derivative can in turn be recovered from parallel transport. In fact
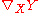can be calculated at a point p, by taking a curve c through p with tangent X, using parallel transport to view the restriction of Y to c as a function in the tangent space at p and then taking the derivative.Orthonormal frame bundle
Let M be a surface embedded in E3. The orientationOrientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
on the surface means that an "outward pointing" normal unit vector n is defined at each point of the surface and hence a determinant can be defined on tangent vectors v and w at that point:
using the usual scalar triple product on E3 (itself a determinant).
An ordered basis or frame v, w in the tangent space is said to be oriented if det(v, w) is positive.
- The tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of M consists of pairs (p, v) in M x E3 such that v lies in the tangent plane to M at p.
- The frame bundleFrame bundleIn mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
E of M consists of triples (p, e1, e2) with an e1, e2 an oriented orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of the tangent plane at p.
- The circle bundle of M consists of pairs (p, v) with ||v|| = 1. It is identical to the frame bundle because for each unit tangent vector v there is a unique unique tangent vector w with det(v, w) = 1.
Since the group of rotations in the plane SO(2) acts simply transitively on oriented orthonormal frames in the plane, it follows that it also acts on the frame or circle bundles of M. The definitions of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, the unit tangent bundle and the (oriented orthonormal) frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
E can be extended to arbitrary surfaces in the usual way. There is a similar identification between the latter two which again become principal SO(2)-bundles. In other words:
There is also a corresponding notion of parallel transport in the setting of frame bundles:
This statement means that any frame on a curve can be parallelly transported along the curve. This is precisely the idea of "moving frames".
Since any unit tangent vector can be completed uniquely to an oriented frame, parallel transport of tangent vectors implies (and is equivalent to) parallel transport of frames. The lift of a geodesic in M turns out to be a geodesic in E for the Sasaki metric (see below). Moreover the Gauss map of M into S2 induces a natural map between the associated frame bundles which is equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
for the actions of SO(2).
Cartan's idea of introducing the frame bundle as a central object was the natural culmination of the theory of moving frame
Moving frame
In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
s, developed in France by Darboux and Goursat. It also echoed parallel developments in Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's theory of relativity
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
. Objects appearing in the formulas of Gauss, such as the Christoffel symbols, can be given a natural geometric interpretation in this framework. Unlike the more intuitive normal bundle
Normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
, easily visualised as a tubular neighbourhood of an embedded surface in E3, the frame bundle is an intrinsic invariant that can be defined independently of an embedding. When there is an embedding, it can also be visualised as a subbundle of the Euclidean frame bundle E3 x SO(3), itself a submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of E3 x M3(R).
Principal connection
.The theory of connections according to Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
, and later Charles Ehresmann
Charles Ehresmann
Charles Ehresmann was a French mathematician who worked on differential topology and category theory. He is known for work on the topology of Lie groups, the jet concept , and his seminar on category theory.He attended the École Normale Supérieure in Paris before performing one year of military...
, revolves around:
- a principal bundle E;
- the exterior differential calculusExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on E.
All "natural" vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s associated with the manifold M, such as the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
or the exterior bundle
Exterior bundle
In mathematics, the exterior bundle of a manifold M is the subbundle of the tensor bundle consisting of all antisymmetric covariant tensors. It has special significance, because one can define a connection-independent derivative on it, namely the exterior derivative.Sections of the exterior bundle...
s, can be constructed from the frame bundle using the representation theory of the structure group K = SO(2), a compact matrix group.
Cartan's definition of a connection can be understood as a way of lifting vector fields on M to vector fields on the frame bundle E invariant under the action of the structure group K. Since parallel transport has been defined as a way of lifting piecewise C1 paths from
M to E, this automatically induces infinitesimally a way to lift vector fields or tangent vectors from M to E. At a point take a path with given tangent vector and then map it to the tangent vector of the lifted path. (For vector fields the curves can be taken to be the integral curves of a local flow.) In this way any vector field X on M can be lifted to a vector field X* on E satisfying
- X* is a vector field on E;
- the map X X* is C∞(M)-linear;
- X* is K-invariant and induces the vector field X on C∞(M)
C∞(E).
Here K acts as a periodic flow on E, so the canonical generator A of its Lie algebra acts as the corresponding vector field, called the vertical vector field A*. It follows from the above conditions that, in the tangent space of an arbitrary point in E, the lifts X* span a two-dimensional subspace of horizontal vectors, forming a complementary subspace to the vertical vectors. The canonical Riemannian metric on E of Shigeo Sasaki is defined by making the horizontal and vertical subspaces orthogonal, giving each subspace its natural inner product.
Horizontal vector fields admit the following characterisation:
- Every K-invariant horizontal vector field on E has the form X* for a unique vector field X on M.
This "universal lift" then immediately induces lifts to vector bundles associated with E and hence allows the covariant derivative, and its generalisation to forms, to be recovered.
If σ is a representation of K on a finite-dimensional vector space V, then the associated vector bundle E XK V over M has a C∞(M)-module of sections that can be identified with
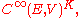
the space of all smooth functions ξ : E → V which are K-equivariant in the sense that
for all x ∈ E and g ∈ K.
The identity representation of SO(2) on R2 corresponds to the tangent bundle of M.
The covariant derivative
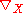is defined on an invariant section ξ by the formula |
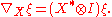The connection on the frame bundle can also be described using K-invariant differential 1-forms on E.
The frame bundle E is a 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
. The space of p-forms
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
on E is denoted Λp(E). It admits a natural action of the structure group K.
Given a connection on the principal bundle E corresponding to a lift X X* of vector fields on M, there is a unique connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
ω in
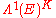, the space of K-invariant 1-forms on E, such that
for all vector fields X on M and
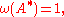
for the vector field A* on E corresponding to the canonical generator A of
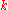.Conversely the lift X* is uniquely characterised by the following properties:
- X* is K-invariant and induces X on M;
- ω(X*)=0.
Cartan structural equations
On the frame bundle E of a surface M there are three canonical 1-forms:- The connection form ω, invariant under the structure group K = SO(2)
- Two tautologous 1-forms θ1 and θ2, transforming according to the basis vectors of the identity representation of K
If π: E
M is the nature projection, the 1-forms θ1 and θ2 are defined by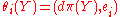where Y is a vector field on E and e1, e2 are the tangent vectors to M of the orthonormal frame.
These 1-forms satisfy the following structural equations, due in this formulation to Cartan:
 |
 |
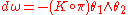where K is the Gaussian curvature on M.
Holonomy and curvature
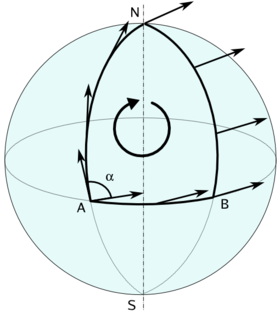
Parallel transport in the frame bundle can be used to show that the Gaussian curvature of a surface M measures the amount of rotation obtained by translating vectors around small curves in M. Holonomy is exactly the phenomenon that occurs when a tangent vector (or orthonormal frame) is parallelly transported around a closed curve. The vector reached when the loop is closed will be a rotation of the original vector, i.e. it will correspond to an element of the rotaion group SO(2), in other words an angle modulo 2π. This is the holonomy of the loop, because the angle does not depend on the choice of starting vector.Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
of two vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s on E. Let U1 and U2 be vector fields on E with corresponding local flows
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
αt and βt.
- Starting at a point A corresponding to x in E, travel
along the integral curve for U1 to the point B at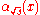 
.
- Travel from B by going
along the integral curve for U2 to the point C at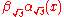 
.
- Travel from C by going
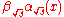along the integral curve for U1 to the point D at 
.
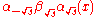- Travel from D by going
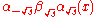along the integral curve for U2 to the point E at 
.
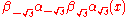In general the end point E will differ from the starting point A. As s
0, the end point E will trace out a curve through A. The Lie bracket [U1,U2] at x is precisely the tangent vector to this curve at A.To apply this theory, introduce vector fields U1, U2 and V on the frame bundle E which are dual to the 1-forms
θ1, θ2 and ω at each point. Thus
Moreover V is invariant under K and U1, U2 transform according to the identity representation of K.
The structural equations of Cartan imply the following Lie bracket relations:
 |
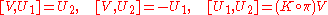The geometrical interpretation of the Lie bracket can be applied to the last of these equations. Since ω(Ui)=0, the flows αt and βt in E are lifts by parallel transport of their projections in M.
Informally the idea is as follows. The starting point A and end point E essentially differ by an element of SO(2), that is an angle of rotation. The area enclosed by the projected path in M is approximately
. So in the limit as s 0, the angle of rotation divided by this area tends to the coefficient of V, i.e. the curvature.This reasoning is made precise in the following result.
In symbols, the holonomy angle mod 2π is given by
 |
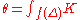where the integral is with respect to the area form on M.
This result implies the relation between Gaussian curvature because as the triangle shrinks in size to a point, the ratio of this angle to the area tends to the Gaussian curvature at the point. The result can be proved by a combination of Stokes's theorem and Cartan's structural equations and can in turn be used to obtain a generalisation of Gauss's theorem on geodesics triangles to more general triangles.
One of the other standard approaches to curvature, through the covariant derivative
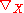, identifies the difference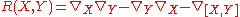as a field of endomorphisms of the tangent bundle, the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
.
Since
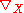is induced by the lifted vector field X* on E, the use of the vector fields Ui and V and their Lie brackets is more or less equivalent to this approach. The vertical vector field W=A* corresponding to the canonical generator A of 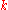could also be added since it commutes with V and satisfies [W,U1] = U2 and [W,U2] = —U1.Example: the 2-sphere
The differential geometry of the 2-sphere can be approached from three different points of view:- analytic geometryAnalytic geometryAnalytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, since the 2-sphere is a submanifoldSubmanifoldIn mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of E3; - group theoryGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, since the compact matrix group SO(3) acts transitively on the 2-sphere as a continuous group of symmetries; - classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, since a rigid 2-sphere can roll on a plane.
S2 can be identified with the unit sphere in E3
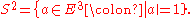
Its tangent bundle T, unit tangent bundle U and oriented orthonormal frame bundle E are given by
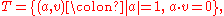
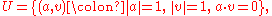
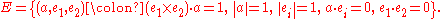
The map sending (a,v) to (a, v, a x v) allows U and E to be identified.
Let
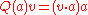
be the orthogonal projection onto the normal vector at a, so that
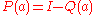
is the orthogonal projection onto the tangent space at a.
The group G = SO(3) acts by rotation on E3 leaving S2 invariant. The stabilizer subgroup K of the vector (1,0,0) in E3 may be identified with SO(2) and hence
This action extends to an action on T, U and E by making G act on each component. G acts transitively on S2 and simply transitively on U and E.
The action of SO(3) on E commutes with the action of SO(2) on E that rotates frames
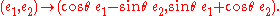
Thus E becomes a principal bundle with structure group K. Taking the G-orbit of the point ((1,0,0),(0,1,0),(0,0,1)), the space E may be identified with G. Under this identification the actions of G and K on E become left and right translation. In other words:
The Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of SO(3) consists of all skew-symmetricSkew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
real 3 x 3 matrices. the adjoint action of G by conjugation on
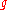reproduces the action of G on E3. The group SU(2) has a 3-dimensional Lie algebra consisting of complex skew-hermitianSkew-Hermitian matrix
In linear algebra, a square matrix with complex entries is said to be skew-Hermitian or antihermitian if its conjugate transpose is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relationA^\dagger = -A,\;...
traceless 2 x 2 matrices, which is isomorphic to
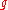. The adjoint action of SU(2) factors through its centre, the matrices ± I. Under these identifications, SU(2) is exhibited as a double cover of SO(3), so that SO(3) = SU(2) / ± I. On the other hand SU(2) is diffeomorphic to the 3-sphere and under this identification the standard Riemannian metric on the 3-sphere becomes the essentially unique biinvariant Riemannian metric on SU(2). Under the quotient by ± I, SO(3) can be identified with the real projective spaceReal projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
of dimension 3 and itself has an essentially unique biinvariant Riemannian metric. The geometric exponential map for this metric at I coincides with the usual exponential function on matrices and thus the geodesics through I are have the form exp Xt where X is a skew-symmetric matrix.
In this case the Sasaki metric agrees with this biinvariant metric on SO(3).
The actions of G on itself, and hence on C∞(G) by left and right translation induce infinitesimal actions of
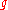on C∞(G) by vector fields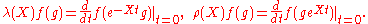The right and left invariant vector fields are related by the formula
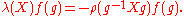
The vector fields λ(X) and ρ(X) commute with right and left translation and give all right and left invariant vector fields on G. Since
C∞(S2) = C∞(G/K) can be identified with C∞(G)K, the function invariant under right translation by K, the operators λ(X) also induces vector fields Π(X) on S2.
Let A, B, C be the standard basis of
given byTheir Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
s [X,Y] = XY – YX are given by
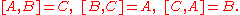
The vector fields λ(A), λ(B), λ(C) form a basis of the tangent space at each point of G.
Similarly the left invariant vector fields ρ(A), ρ(B), ρ(C) form a basis of the tangent space at each point of G.
Let α, β, γ be the corresponding dual basis of left invariant 1-forms on G. The Lie bracket relations imply the Maurer-Cartan equations
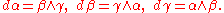
These are also the corresponding components of the Maurer-Cartan form
Maurer-Cartan form
In mathematics, the Maurer–Cartan form for a Lie group G is a distinguished differential one-form on G that carries the basic infinitesimal information about the structure of G...
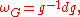
a left invariant matrix-valued 1-form on G, which satisfies the relation
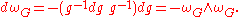
The inner product on
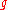defined by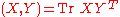is invariant under the adjoint action. Let π be the orthogonal projection onto the subspace generated by A, i.e. onto
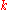, the Lie algebra of K. For X in 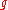, the lift of the vector field Π(X) from C∞(G/K) to C∞(G) is given by the formula |
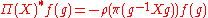This lift is G-equivariant on vector fields of the form Π(X) and has a unique extension to more general vector fields on G / K.
The left invariant 1-form α is the connection form ω on G corresponding to this lift. The other two 1-forms in the Cartan structural equations are given by θ1 = β and θ2 = γ. The structural equations themselves are just the Maurer-Cartan equations. In other words;
Since α is the connection form,
- vertical vector fields on G are those of the form f · λ(A) with f in C∞(G);
- horizontal vector fields on G are those of the form f1 · λ(B) + f2 · λ(C) with fi in C∞(G).
The existence of the basis vector fields λ(A), λ(B), λ(C) shows that SO(3) is parallelizable. This is not true for SO(3)/SO(2) by the hairy ball theorem
Hairy ball theorem
The hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...
: S2 does not admit any nowhere vanishing vector fields.
Parallel transport in the frame bundle amounts to lifting a path from SO(3)/SO(2) to SO(3). It can be accomplished by directly solving a matrix-valued ordinary differential equation ("transport equation") of the form gt = A · g where A(t) is skew-symmetric and g takes values in SO(3).
In fact it is equivalent and more convenient to lift a path from SO(3)/O(2) to SO(3). Note that O(2) is the normaliser of SO(2) in SO(3) and the quotient group O(2)/SO(2), the so called the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
, is a group of order 2 which acts on SO(3)/SO(2) = S2 as the antipodal map. The quotient SO(3)/O(2) is the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
. It can be identified with space of rank one or rank two projections Q in M3(R). Taking Q to be a rank 2 projection and setting F = 2Q − I, a model of the surface SO(3)/O(2) is given by
matrices F satisfying F2 = I, F = FT and Tr F = 1. Taking F0= diag (–1,1,1) as base point, every F can be written in the form g F0 g−1.
If Q(t) is the corresponding path of rank 2 projections, the conditions for parallel transport are
Set A = ½Ft F. Since F2 = I and F is symmetric, A is skew-symmetric and satisfies
QAQ = 0.
The unique solution g(t) of the ordinary differential equation
with initial condition g(0) = I guaranteed by the Picard–Lindelöf theorem
Picard–Lindelöf theorem
In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
, must have gTg constant and therefore I, since
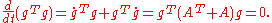
Moreover
since g−1Fg has derivative 0:
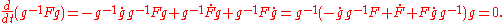
Hence Q = g Q0 g−1. The condition QAQ=0 implies Q gt g−1 Q = 0 and hence that Q0 g−1 gt Q0 =0.
There is another kinematic way of understanding parallel transport and geodesic curvature in terms of "rolling without slipping or twisting". Although well known to differential geometers since the early part of the twentieth century, it has also been applied to problems in engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
and robotics
Robotics
Robotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
. Consider the 2-sphere as a rigid body in three dimensional space rolling without slipping or twisting on a horizontal plane. The point of contact will describe a curve in the plane and on the surface. At each point of contact the different tangent planes of the sphere can be identified with the horizontal plane itself and hence with one another.
- The usual curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of the planar curve is the geodesic curvature of the curve traced on the sphere. - This identification of the tangent planes along the curve corresponds to parallel transport.
This is particularly easy to visualize for a sphere: it is exactly the way a marble can be rolled along a perfectly flat table top.
The roles of the plane and the sphere can be reversed to provide an alternative but equivalent point of view. The sphere is regarded as fixed and the plane has to roll without slipping or twisting along the given curve on the sphere.
Embedded surfaces
When a surface M is embedded in E3, the Gauss map from M S2 extends to a SO(2)-equivariant map between the orthonormal frame bundles E SO(3). Indeed the triad consisting of the tangent frame and the normal vector gives an element of SO(3).In 1956 Kobayashi proved that:
This means that the forms ω, θ1 and θ2 on E are obtained by pulling back those on SO(3); and that lifting paths from M to E can be accomplished by mapping the path to the 2-sphere, lifting the path to SO(3) and then pulling back the lift to E. Thus for embedded surfaces, the 2-sphere with the principal connection on its frame bundle provides a "universal model", the prototype for the universal bundles discussed in .
In more concrete terms this allows parallel transport to be described explicitly using the transport equation. Parallel transport along a curve c(t), with t taking values in [0,1], starting from a tangent from a tangent vector v0 also amounts to finding a map v(t) from [0,1] to R3 such that
- v(t) is a tangent vector to M at c(t) with v(0) = v0.
- the velocity vectorVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
is normal to the surface at c(t), i.e. P(c(t))v(t)=0.
This always has a unique solution, called the parallel transport of v0 along c.
The existence of parallel transport can be deduced using the analytic method described for SO(3)/SO(2), which from a path into the rank two projections
Q(t) starting at Q0 produced a path g(t) in SO(3) starting at I such that
g(t) is the unique solution of the transport equation
| gtg−1 = ½ Ft F |
with g(0) = I and F = 2Q − I. Applying this with Q(t) = P(c(t)), it follows that, given a tangent vector v0 in the tangent space to M at c(0),
the vector v(t)=g(t)v0 lies in the tangent space to M at c(t) and satisfies the equation
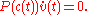
It therefore is exactly the parallel transport of v along the curve c. In this case the length of the vector v(t) is constant. More generally if another initial tangent vector u0 is taken instead of v0, the inner product (v(t),u(t)) is constant. The tangent spaces along the curve c(t) are thus canonically identified as inner product spaces by parallel transport so that parallel transport gives an isometry between the tangent planes. The condition on the velocity vector
may be rewritten in terms of the covariant derivative as
 |
the defining equation for parallel transport.
The kinematic way of understanding parallel transport for the sphere applies equally well to any closed surface in E3 regarded as a rigid body in three dimensional space rolling without slipping or twisting on a horizontal plane. The point of contact will describe a curve in the plane and on the surface. As for the sphere, the usual curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of the planar curve equals the geodesic curvature of the curve traced on the surface.
This geometric way of viewing parallel transport can also be directly expressed in the language of geometry. The envelope
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of the tangent planes to M along a curve c is a surface with vanishing Gaussian curvature, which by Minding's theorem, must be locally isometric to the Euclidean plane. This identification allows parallel transport to be defined, because in the Euclidean plane all tangent planes are identified with the space itself.
There is another simple way of constructing the connection form ω using the embedding of M in E3.
The tangent vectors e1 and e2 of a frame on M define smooth functions from E with values in R3, so each gives a 3-vector of functions and in particular de1 is a 3-vector of 1-forms on E.
The connection form is given by
 |
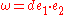taking the usual scalar product on 3-vectors.
Gauss-Codazzi equations
When M is embedded in E3, two other 1-forms ψ and χ can be defined on the frame bundle E using the shape operator. Indeed the Gauss map induces a K-equivariant map of E into SO(3), the frame bundle of S2 = SO(3)/SO(2). The formω is the pullback
Pullback
Suppose that φ:M→ N is a smooth map between smooth manifolds M and N; then there is an associated linear map from the space of 1-forms on N to the space of 1-forms on M. This linear map is known as the pullback , and is frequently denoted by φ*...
of one of the three right invariant Maurer-Cartan form
Maurer-Cartan form
In mathematics, the Maurer–Cartan form for a Lie group G is a distinguished differential one-form on G that carries the basic infinitesimal information about the structure of G...
s on SO(3). The 1-forms ψ and χ are defined to be the pullbacks of the other two.
These 1-forms satisfy the following structure equations:
 |
 |
 |
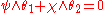The Gauss–Codazzi equations
Gauss–Codazzi equations
In Riemannian geometry, the Gauss–Codazzi–Mainardi equations are fundamental equations in the theory of embedded hypersurfaces in a Euclidean space, and more generally submanifolds of Riemannian manifolds...
for χ, ψ and ω follow immediately from the Maurer-Cartan equations for the three right invariant 1-forms on SO(3).