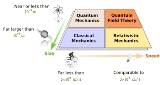
Branches of physics
Encyclopedia

Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
deals with a wide variety of systems, there are certain theories that are used by all physicists. Each of these theories were experimentally tested numerous times and found correct as an approximation of Nature (within a certain domain of validity). For instance, the theory of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
accurately describes the motion of objects, provided they are much larger than atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s and moving at much less than the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. These theories continue to be areas of active research; for instance, a remarkable aspect of classical mechanics known as chaos
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
was discovered in the 20th century, three centuries after the original formulation of classical mechanics by Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
(1642–1727). These "central theories" are important tools for research into more specialized topics, and any physicist, regardless of his or her specialization, is expected to be literate in them.
Classical mechanics

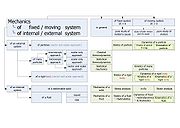
Classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
is a model dada of the physics of force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s acting upon bodies. It is often referred to as "Newtonian mechanics" after Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and his laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
. Mechanics is subdivided into statics
Statics
Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
, which models objects at rest, kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
, which models objects in motion, and dynamics
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
, which models objects subjected to forces. The classical mechanics of continuous and deformable objects is continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, which can itself be broken down into solid mechanics
Solid mechanics
Solid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
and fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
according to the state of matter being studied. The latter, the mechanics of liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
s and gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
es, includes hydrostatics, hydrodynamics, pneumatics
Pneumatics
Pneumatics is a branch of technology, which deals with the study and application of use of pressurized gas to effect mechanical motion.Pneumatic systems are extensively used in industry, where factories are commonly plumbed with compressed air or compressed inert gases...
, aerodynamics
Aerodynamics
Aerodynamics is a branch of dynamics concerned with studying the motion of air, particularly when it interacts with a moving object. Aerodynamics is a subfield of fluid dynamics and gas dynamics, with much theory shared between them. Aerodynamics is often used synonymously with gas dynamics, with...
, and other fields.
An important concept of mechanics is the identification of conserved energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
and momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, which lead to the Lagrangian
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
and Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
reformulations of Newton's laws. Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
for statistical and Hamiltonian mechanics is a classical nineteenth century result which describes the behavior of the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
distribution function
Distribution function
In molecular kinetic theory in physics, a particle's distribution function is a function of seven variables, f, which gives the number of particles per unit volume in phase space. It is the number of particles per unit volume having approximately the velocity near the place and time...
. Liouville's theorem has a suggestive formulation, the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
, which encodes Hamilton's equations of classical mechanics, and has analogies with the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
in quantum mechanics.
A relatively recent result of considerations concerning the dynamics of nonlinear systems is chaos theory
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
, the study of systems in which small changes in a variable may have large effects.
Thermodynamics and statistical mechanics
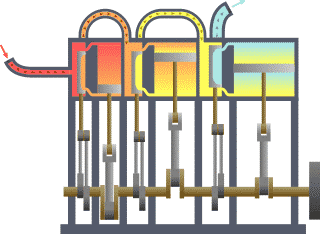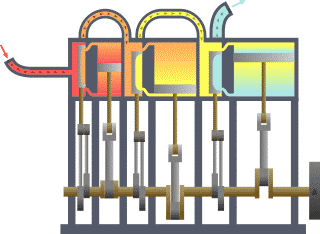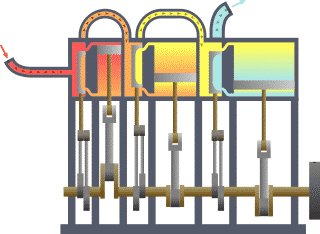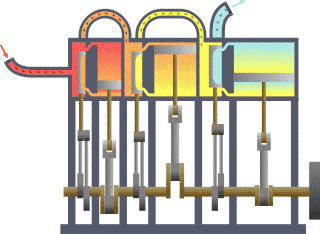
The Feynman Lectures on Physics
The Feynman Lectures on Physics is a 1964 physics textbook by Richard P. Feynman, Robert B. Leighton and Matthew Sands, based upon the lectures given by Feynman to undergraduate students at the California Institute of Technology in 1961–63. It includes lectures on mathematics, electromagnetism,...
is about the existence of atoms, which Feynman considered to be the most compact statement of physics, from which science could easily result even if all other knowledge was lost. By modeling matter as collections of hard spheres, it is possible to describe the kinetic theory of gases, upon which classical thermodynamics is based.
Thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
studies the effects of changes in temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, and volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
on physical system
Physical system
In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...
s at the macroscopic
Macroscopic
The macroscopic scale is the length scale on which objects or processes are of a size which is measurable and observable by the naked eye.When applied to phenomena and abstract objects, the macroscopic scale describes existence in the world as we perceive it, often in contrast to experiences or...
scale, and the transfer of energy as heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
. Historically, thermodynamics developed out of need to increase the efficiency of early steam engine
Steam engine
A steam engine is a heat engine that performs mechanical work using steam as its working fluid.Steam engines are external combustion engines, where the working fluid is separate from the combustion products. Non-combustion heat sources such as solar power, nuclear power or geothermal energy may be...
s.
The starting point for most thermodynamic considerations are the laws of thermodynamics
Laws of thermodynamics
The four laws of thermodynamics summarize its most important facts. They define fundamental physical quantities, such as temperature, energy, and entropy, in order to describe thermodynamic systems. They also describe the transfer of energy as heat and work in thermodynamic processes...
, which postulate that energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
can be exchanged between physical systems as heat or work
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
. They also postulate the existence of a quantity named entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
, which can be defined for any system. In thermodynamics, interactions between large ensembles of objects are studied and categorized. Central to this are the concepts of system and surroundings. A system is composed of particles, whose average motions define its properties, which in turn are related to one another through equations of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
. Properties can be combined to express internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
and thermodynamic potentials
Thermodynamic potentials
A thermodynamic potential is a scalar function used to represent the thermodynamic state of a system. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886. Josiah Willard Gibbs in his papers used the term fundamental functions. One main thermodynamic potential that has a...
, which are useful for determining conditions for equilibrium
Dynamic equilibrium
A dynamic equilibrium exists once a reversible reaction ceases to change its ratio of reactants/products, but substances move between the chemicals at an equal rate, meaning there is no net change. It is a particular example of a system in a steady state...
and spontaneous process
Spontaneous process
A spontaneous process is the time-evolution of a system in which it releases free energy and moves to a lower, more thermodynamically stable energy state...
es.
Electromagnetism
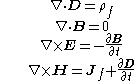 |
| Maxwell's equations Maxwell's equations Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations... of electromagnetism Electromagnetism Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation... |
Electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
describes the interaction of charged particles with electric and magnetic field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
s. It can be divided into electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, the study of interactions between charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
s at rest, and electrodynamics, the study of interactions between moving charges and radiation
Radiation
In physics, radiation is a process in which energetic particles or energetic waves travel through a medium or space. There are two distinct types of radiation; ionizing and non-ionizing...
. The classical theory of electromagnetism is based on the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
law and Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
. Light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
is an oscillating electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
that is radiated from accelerating charged particles. Thus, all of optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, the study of the nature and propagation of light, can be reduced to electromagnetic interactions. Two major fields of optics are geometric optics or "classical optics", and physical optics
Physical optics
In physics, physical optics, or wave optics, is the branch of optics which studies interference, diffraction, polarization, and other phenomena for which the ray approximation of geometric optics is not valid...
which studies the electromagnetic properties of light to achieve greater understanding of phenomena such as interference, diffraction, and polarization.
A more recent development is quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, which incorporates the laws of quantum theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
in order to explain the interaction of electromagnetic radiation with matter. Relativistic electrodynamics accounts for relativistic
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
corrections to the motions of charged particles when their speeds approach the speed of light. It applies to phenomena involved with particle accelerators and electron tubes carrying high voltages and current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
s.
Relativity
The special theory of relativityTheory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
enjoys a relationship with electromagnetism and mechanics; that is, the principle of relativity
Principle of relativity
In physics, the principle of relativity is the requirement that the equations describing the laws of physics have the same form in all admissible frames of reference....
and the principle of stationary action in mechanics can be used to derive Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, and vice versa.
The theory of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
was proposed in 1905 by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
in his article "On the Electrodynamics of Moving Bodies". The title of the article refers to the fact that special relativity resolves an inconsistency between Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
and classical mechanics. The theory is based on two postulates
Postulates of special relativity
- Postulates of special relativity :1. First postulate 2. Second postulate - Alternate Derivations of Special Relativity :...
: (1) that the mathematical forms of the laws of physics
Physical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
are invariant in all inertial systems
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
; and (2) that the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in a vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
is constant and independent of the source or observer. Reconciling the two postulates requires a unification of space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
into the frame-dependent concept of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
.
General relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
is the geometrical
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
theory
Theory
The English word theory was derived from a technical term in Ancient Greek philosophy. The word theoria, , meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action...
of gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
published by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
in 1915/16. It unifies special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, Newton's law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
, and the insight that gravitation can be described by the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
. In general relativity, the curvature of space-time is produced by the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of matter and radiation.
Quantum mechanics

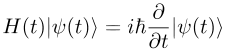
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
is the branch of physics treating atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
ic and subatomic
Subatomic particle
In physics or chemistry, subatomic particles are the smaller particles composing nucleons and atoms. There are two types of subatomic particles: elementary particles, which are not made of other particles, and composite particles...
systems and their interaction with radiation
Radiation
In physics, radiation is a process in which energetic particles or energetic waves travel through a medium or space. There are two distinct types of radiation; ionizing and non-ionizing...
. It is based on the observation that all forms of energy are released in discrete units or bundles called "quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
". Remarkably, quantum theory typically permits only probable
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
or statistical
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
calculation of the observed features of subatomic particles, understood in terms of wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s. The Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
plays the role in quantum mechanics that Newton's laws
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
and conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
serve in classical mechanics — i.e., it predicts the future behavior of a dynamic system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
— and is a wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
that is used to solve for wavefunctions.
For example, the light, or electromagnetic radiation emitted or absorbed by an atom has only certain frequencies
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
(or wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
s), as can be seen from the line spectrum
Emission spectrum
The emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted by the element's atoms or the compound's molecules when they are returned to a lower energy state....
associated with the chemical element represented by that atom. The quantum theory shows that those frequencies correspond to definite energies of the light quanta, or photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s, and result from the fact that the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s of the atom can have only certain allowed energy values, or levels; when an electron changes from one allowed level to another, a quantum of energy is emitted or absorbed whose frequency is directly proportional to the energy difference between the two levels. The photoelectric effect
Photoelectric effect
In the photoelectric effect, electrons are emitted from matter as a consequence of their absorption of energy from electromagnetic radiation of very short wavelength, such as visible or ultraviolet light. Electrons emitted in this manner may be referred to as photoelectrons...
further confirmed the quantization of light.
In 1924, Louis de Broglie proposed that not only do light waves sometimes exhibit particle-like properties, but particles may also exhibit wavelike properties. Two different formulations of quantum mechanics were presented following de Broglie’s suggestion. The wave mechanics of Erwin Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
(1926) involves the use of a mathematical entity, the wave function, which is related to the probability of finding a particle at a given point in space. The matrix mechanics
Matrix mechanics
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925.Matrix mechanics was the first conceptually autonomous and logically consistent formulation of quantum mechanics. It extended the Bohr Model by describing how the quantum jumps...
of Werner Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
(1925) makes no mention of wave functions or similar concepts but was shown to be mathematically equivalent to Schrödinger’s theory. A particularly important discovery of the quantum theory is the uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
, enunciated by Heisenberg in 1927, which places an absolute theoretical limit on the accuracy of certain measurements; as a result, the assumption by earlier scientists that the physical state of a system could be measured exactly and used to predict future states had to be abandoned. Quantum mechanics was combined with the theory of relativity in the formulation of Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
. Other developments include quantum statistics, quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, concerned with interactions between charged particles and electromagnetic fields; and its generalization, quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
Interdisciplinary fields
To the interdisciplinary fields, which define partially sciences of their own, belong e.g. the- Chemical PhysicsChemical physicsChemical physics is a subdiscipline of chemistry and physics that investigates physicochemical phenomena using techniques from atomic and molecular physics and condensed matter physics; it is the branch of physics that studies chemical processes from the point of view of physics...
, the science of physical relations in chemistryChemistryChemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds.... - GeophysicsGeophysicsGeophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...
, the sciences of physical relations on our planet - EconophysicsEconophysicsEconophysics is an interdisciplinary research field, applying theories and methods originally developed by physicists in order to solve problems in economics, usually those including uncertainty or stochastic processes and nonlinear dynamics...
, dealing with physical processes and their relations in the science of economyEconomyAn economy consists of the economic system of a country or other area; the labor, capital and land resources; and the manufacturing, trade, distribution, and consumption of goods and services of that area...
Summary
The table below lists the core theories along with many of the concepts they employ.| Theory | Major subtopics | Concepts |
|---|---|---|
| Classical mechanics Classical mechanics In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces... |
Newton's laws of motion Newton's laws of motion Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces... , Lagrangian mechanics Lagrangian mechanics Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788.... , Hamiltonian mechanics Hamiltonian mechanics Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without... , Kinematics Kinematics Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion.... , Statics Statics Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity... , Dynamics Dynamics (mechanics) In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion... , Chaos theory Chaos theory Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the... , Acoustics Acoustics Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics... , Fluid dynamics Fluid dynamics In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics... , Continuum mechanics Continuum mechanics Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles... |
Density Density The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight... , Dimension Dimension In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it... , Gravity, Space Space Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum... , Time Time Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects.... , Motion Motion (physics) In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as... , Length Length In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire... , Position, Velocity Velocity In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ... , Acceleration Acceleration In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ... , Galilean invariance Galilean invariance Galilean invariance or Galilean relativity is a principle of relativity which states that the fundamental laws of physics are the same in all inertial frames... , Mass Mass Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:... , Momentum Momentum In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object... , Impulse Impulse In classical mechanics, an impulse is defined as the integral of a force with respect to time. When a force is applied to a rigid body it changes the momentum of that body... , Force, Energy Energy In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems... , Angular velocity Angular velocity In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per... , Angular momentum Angular momentum In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system... , Moment of inertia Moment of inertia In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation... , Torque Torque Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist.... , Conservation law Conservation law In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves.... , Harmonic oscillator Harmonic oscillator In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant.... , Wave Wave In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass... , Work Mechanical work In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work... , Power Power (physics) In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit... , Lagrangian, Hamiltonian, Tait-Bryan angles, Euler angles Euler angles The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required... |
| Electromagnetism Electromagnetism Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation... |
Electrostatics Electrostatics Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges.... , Electrodynamics, Electricity Electricity Electricity is a general term encompassing a variety of phenomena resulting from the presence and flow of electric charge. These include many easily recognizable phenomena, such as lightning, static electricity, and the flow of electrical current in an electrical wire... , Magnetism Magnetism Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well... , Magnetostatics Magnetostatics Magnetostatics is the study of magnetic fields in systems where the currents are steady . It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching events that... , Maxwell's equations Maxwell's equations Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations... , Optics Optics Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light... |
Capacitance Capacitance In electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor... , Electric charge Electric charge Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two... , Current, Electrical conductivity, Electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... , Electric permittivity Permittivity In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how... , Electric potential Electric potential In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there... , Electrical resistance Electrical resistance The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical... , Electromagnetic field Electromagnetic field An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction... , Electromagnetic induction Electromagnetic induction Electromagnetic induction is the production of an electric current across a conductor moving through a magnetic field. It underlies the operation of generators, transformers, induction motors, electric motors, synchronous motors, and solenoids.... , Electromagnetic radiation Electromagnetic radiation Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space... , Gaussian surface Gaussian surface A Gaussian surface is a closed surface in three dimensional space through which the flux of an electromagnetic field is calculated. It is an arbitrary closed surface S=\partial V used in conjunction with Gauss's law in order to calculate the total enclosed electric charge by performing a surface... , Magnetic field Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... , Magnetic flux Magnetic flux Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber... , Magnetic monopole Magnetic monopole A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring... , Magnetic permeability |
| Thermodynamics Thermodynamics Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation... and Statistical mechanics Statistical mechanics Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably... |
Heat engine Heat engine In thermodynamics, a heat engine is a system that performs the conversion of heat or thermal energy to mechanical work. It does this by bringing a working substance from a high temperature state to a lower temperature state. A heat "source" generates thermal energy that brings the working substance... , Kinetic theory Kinetic theory The kinetic theory of gases describes a gas as a large number of small particles , all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container... |
Boltzmann's constant, Conjugate variables Conjugate variables (thermodynamics) In thermodynamics, the internal energy of a system is expressed in terms of pairs of conjugate variables such as temperature/entropy or pressure/volume. In fact all thermodynamic potentials are expressed in terms of conjugate pairs.... , Enthalpy Enthalpy Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a... , Entropy Entropy Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when... , Equation of state Equation of state In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions... , Equipartition theorem Equipartition theorem In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition... , Thermodynamic free energy Thermodynamic free energy The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to... , Heat Heat In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between... , Ideal gas law Ideal gas law The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law... , Internal energy Internal energy In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal... , Laws of thermodynamics Laws of thermodynamics The four laws of thermodynamics summarize its most important facts. They define fundamental physical quantities, such as temperature, energy, and entropy, in order to describe thermodynamic systems. They also describe the transfer of energy as heat and work in thermodynamic processes... , Maxwell relations Maxwell relations Maxwell's relations are a set of equations in thermodynamics which are derivable from the definitions of the thermodynamic potentials. The Maxwell relations are statements of equality among the second derivatives of the thermodynamic potentials. They follow directly from the fact that the order of... , Irreversible process Non-equilibrium thermodynamics Non-equilibrium thermodynamics is a branch of thermodynamics that deals with systems that are not in thermodynamic equilibrium. Most systems found in nature are not in thermodynamic equilibrium; for they are changing or can be triggered to change over time, and are continuously and discontinuously... , Ising model Ising model The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors... , Mechanical action Action (physics) In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is... , Partition function Partition function (statistical mechanics) Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas... , Pressure Pressure Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :... , Reversible process Reversible process (thermodynamics) In thermodynamics, a reversible process, or reversible cycle if the process is cyclic, is a process that can be "reversed" by means of infinitesimal changes in some property of the system without loss or dissipation of energy. Due to these infinitesimal changes, the system is in thermodynamic... , Spontaneous process Spontaneous process A spontaneous process is the time-evolution of a system in which it releases free energy and moves to a lower, more thermodynamically stable energy state... , State function State function In thermodynamics, a state function, function of state, state quantity, or state variable is a property of a system that depends only on the current state of the system, not on the way in which the system acquired that state . A state function describes the equilibrium state of a system... , Statistical ensemble Statistical ensemble (mathematical physics) In mathematical physics, especially as introduced into statistical mechanics and thermodynamics by J. Willard Gibbs in 1878, an ensemble is an idealization consisting of a large number of mental copies of a system, considered all at once, each of which represents a possible state that the real... , Temperature Temperature Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot... , Thermodynamic equilibrium Thermodynamic equilibrium In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance... , Thermodynamic potential, Thermodynamic processes Thermodynamic processes A thermodynamic process may be defined as the energetic development of a thermodynamic system proceeding from an initial state to a final state. Paths through the space of thermodynamic variables are often specified by holding certain thermodynamic variables constant... , Thermodynamic state Thermodynamic state A thermodynamic state is a set of values of properties of a thermodynamic system that must be specified to reproduce the system. The individual parameters are known as state variables, state parameters or thermodynamic variables. Once a sufficient set of thermodynamic variables have been... , Thermodynamic system, Viscosity Viscosity Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity... , Volume Volume Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains.... , Work Work (thermodynamics) In thermodynamics, work performed by a system is the energy transferred to another system that is measured by the external generalized mechanical constraints on the system. As such, thermodynamic work is a generalization of the concept of mechanical work in mechanics. Thermodynamic work encompasses... , Granular material Granular material A granular material is a conglomeration of discrete solid, macroscopic particles characterized by a loss of energy whenever the particles interact . The constituents that compose granular material must be large enough such that they are not subject to thermal motion fluctuations... |
| Quantum mechanics Quantum mechanics Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic... |
Path integral formulation Path integral formulation The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics... , Scattering theory Scattering theory In mathematics and physics, scattering theory is a framework for studying and understanding the scattering of waves and particles. Prosaically, wave scattering corresponds to the collision and scattering of a wave with some material object, for instance sunlight scattered by rain drops to form a... , Schrödinger equation Schrödinger equation The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time.... , Quantum field theory Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... , Quantum statistical mechanics Quantum statistical mechanics Quantum statistical mechanics is the study of statistical ensembles of quantum mechanical systems. A statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be... |
Adiabatic approximation Born-Oppenheimer approximation In quantum chemistry, the computation of the energy and wavefunction of an average-size molecule is a formidable task that is alleviated by the Born–Oppenheimer approximation, named after Max Born and J. Robert Oppenheimer. For instance the benzene molecule consists of 12 nuclei and 42... , Blackbody radiation, Correspondence principle Correspondence principle In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers.... , Free particle Free particle In physics, a free particle is a particle that, in some sense, is not bound. In classical physics, this means the particle is present in a "field-free" space.-Classical Free Particle:The classical free particle is characterized simply by a fixed velocity... , Hamiltonian Hamiltonian (quantum mechanics) In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system... , Hilbert space Hilbert space The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions... , Identical particles Identical particles Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two... , Matrix Mechanics Matrix mechanics Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925.Matrix mechanics was the first conceptually autonomous and logically consistent formulation of quantum mechanics. It extended the Bohr Model by describing how the quantum jumps... , Planck's constant, Observer effect Observer effect (physics) In physics, the term observer effect refers to changes that the act of observation will make on the phenomenon being observed. This is often the result of instruments that, by necessity, alter the state of what they measure in some manner... , Operators, Quanta Quantum In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete... , Quantization Quantization (physics) In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the... , Quantum entanglement Quantum entanglement Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is... , Quantum harmonic oscillator Quantum harmonic oscillator The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics... , Quantum number Quantum number Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously... , Quantum tunneling, Schrödinger's cat Schrödinger's cat Schrödinger's cat is a thought experiment, usually described as a paradox, devised by Austrian physicist Erwin Schrödinger in 1935. It illustrates what he saw as the problem of the Copenhagen interpretation of quantum mechanics applied to everyday objects. The scenario presents a cat that might be... , Dirac equation Dirac equation The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and... , Spin Spin (physics) In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,... , Wavefunction Wavefunction Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of... , Wave mechanics, Wave-particle duality, Zero-point energy Zero-point energy Zero-point energy is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state. All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature... , Pauli Exclusion Principle Pauli exclusion principle The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles... , Heisenberg Uncertainty Principle |
| Relativity Theory of relativity The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance.... |
Special relativity Special relativity Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's... , General relativity General relativity General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics... , Einstein field equations Einstein field equations The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy... |
Covariance General covariance In theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations... , Einstein manifold Einstein manifold In differential geometry and mathematical physics, an Einstein manifold is a Riemannian or pseudo-Riemannian manifold whose Ricci tensor is proportional to the metric... , Equivalence principle Equivalence principle In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually... , Four-momentum Four-momentum In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime... , Four-vector Four-vector In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis... , General principle of relativity, Geodesic motion Geodesic (general relativity) In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational, force is a particular type of geodesic... , Gravity, Gravitoelectromagnetism, Inertial frame of reference Inertial frame of reference In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not... , Invariance Invariant (physics) In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another... , Length contraction Length contraction In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer... , Lorentzian manifold Pseudo-Riemannian manifold In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the... , Lorentz transformation Lorentz transformation In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik... , Mass-energy equivalence Mass-energy equivalence In physics, mass–energy equivalence is the concept that the mass of a body is a measure of its energy content. In this concept, mass is a property of all energy, and energy is a property of all mass, and the two properties are connected by a constant... , Metric Metric (mathematics) In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric... , Minkowski diagram Minkowski diagram The Minkowski diagram was developed in 1908 by Hermann Minkowski and provides an illustration of the properties of space and time in the special theory of relativity. It allows a quantitative understanding of the corresponding phenomena like time dilation and length contraction without mathematical... , Minkowski space Minkowski space In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated... , Principle of Relativity Principle of relativity In physics, the principle of relativity is the requirement that the equations describing the laws of physics have the same form in all admissible frames of reference.... , Proper length Proper length In relativistic physics, proper length is an invariant measure of the distance between two spacelike-separated events, or of the length of a spacelike path within a spacetime.... , Proper time Proper time In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two... , Reference frame Frame of reference A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an... , Rest energy, Rest mass, Relativity of simultaneity Relativity of simultaneity In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur... , Spacetime Spacetime In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions... , Special principle of relativity, Speed of light Speed of light The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time... , Stress-energy tensor Stress-energy tensor The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields... , Time dilation Time dilation In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at... , Twin paradox Twin paradox In physics, the twin paradox is a thought experiment in special relativity, in which a twin makes a journey into space in a high-speed rocket and returns home to find he has aged less than his identical twin who stayed on Earth... , World line World line In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein... |

