Vector (spatial) - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, and engineering

Engineering

Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...

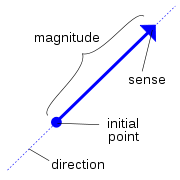
, a Euclidean vector (sometimes called a geometric or spatial vector, or – as here – simply a vector) is a geometric object that has both a magnitude

Magnitude (mathematics)

The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....

(or length) and direction. A Euclidean vector is frequently represented by a line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

with a definite direction, or graphically as an arrow, connecting an initial point A with a terminal point B, and denoted by

A vector is what is needed to "carry" the point A to the point B; the Latin word vector means "carrier". The magnitude of the vector is the distance between the two points and the direction refers to the direction of displacement from A to B. Many algebraic operations on real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s such as addition

Addition

Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....

, subtraction

Subtraction

In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...

, multiplication

Multiplication

Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....

, and negation

Negation

In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...

have close analogues for vectors, operations which obey the familiar algebraic laws of commutativity

Commutativity

In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...

, associativity

Associativity

In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...

, and distributivity

Distributivity

In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...

. These operations and associated laws qualify Euclidean

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

vectors as an example of the more generalized concept of vectors defined simply as elements of a vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

.

Vectors play an important role in physics

Physics

: velocity

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

and acceleration

Acceleration

In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...

of a moving object and force

Force

In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...

s acting on it are all described by vectors. Many other physical quantities can be usefully thought of as vectors. Although most of them do not represent distances (such as position or displacement

Displacement (vector)

A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...

), their magnitude and direction can be still represented by the length and direction of an arrow. The mathematical representation of a physical vector depends on the coordinate system

Coordinate system

In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...

used to describe it. Other vector-like objects that describe physical quantities and transform in a similar way under changes of the coordinate system include pseudovector

Pseudovector

In physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...

s and tensor

Tensor

Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...

Overview

A vector is a geometric entity characterized by a magnitude

Magnitude (mathematics)

(in mathematics a number, in physics a number times a unit) and a direction. In rigorous mathematical treatments, a vector is defined as a directed line segment, or arrow, in a Euclidean space. When it becomes necessary to distinguish it from vectors as defined elsewhere

Vector space

, this is sometimes referred to as a geometric, spatial, or Euclidean vector.

As an arrow in Euclidean space, a vector possesses a definite initial point and terminal point. Such a vector is called a bound vector. When only the magnitude and direction of the vector matter, then the particular initial point is of no importance, and the vector is called a free vector. Thus two arrows

and

in space represent the same free vector if they have the same magnitude and direction: that is, they are equivalent if the quadrilateral ABB′A′ is a parallelogram

Parallelogram

In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...

. If the Euclidean space is equipped with a choice of origin

Origin (mathematics)

In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...

, then a free vector is equivalent to the bound vector of the same magnitude and direction whose initial point is the origin.

The term vector also has generalizations to higher dimensions and to more formal approaches with much wider applications.

Examples in one dimension

Since the physicist's concept of force has a direction and a magnitude, it may be seen as a vector. As an example, consider a rightward force F of 15 newtons. If the positive axis is also directed rightward, then F is represented by the vector 15 N, and if positive points leftward, then the vector for F is −15 N. In either case, the magnitude of the vector is 15 N. Likewise, the vector representation of a displacement Δs of 4 meters to the right would be 4 m or −4 m, and its magnitude would be 4 m regardless.

In physics and engineering

Vectors are fundamental in the physical sciences. They can be used to represent any quantity that has both a magnitude and direction, such as velocity

Velocity

, the magnitude of which is speed

Speed

In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...

. For example, the velocity 5 meters per second upward could be represented by the vector (0,5) (in 2 dimensions with the positive y axis as 'up'). Another quantity represented by a vector is force

Force

, since it has a magnitude and direction. Vectors also describe many other physical quantities, such as displacement

Displacement (vector)

, acceleration

Acceleration

, momentum

Momentum

In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...

, and angular momentum

Angular momentum

In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...

. Other physical vectors, such as the electric

Electric field

In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...

and magnetic field

Magnetic field

A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...

, are represented as a system of vectors at each point of a physical space; that is, a vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

In Cartesian space

In the Cartesian coordinate system

Cartesian coordinate system

A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...

, a vector can be represented by identifying the coordinates of its initial and terminal point. For instance, the points A = (1,0,0) and B = (0,1,0) in space determine the free vector

pointing from the point x=1 on the x-axis to the point y=1 on the y-axis.

Typically in Cartesian coordinates, one considers primarily bound vectors. A bound vector is determined by the coordinates of the terminal point, its initial point always having the coordinates of the origin O = (0,0,0). Thus the bound vector represented by (1,0,0) is a vector of unit length pointing from the origin up the positive x-axis.

The coordinate representation of vectors allows the algebraic features of vectors to be expressed in a convenient numerical fashion. For example, the sum of the vectors (1,2,3) and (−2,0,4) is the vector

(1, 2, 3) + (−2, 0, 4) = (1 − 2, 2 + 0, 3 + 4) = (−1, 2, 7).

Euclidean and affine vectors

In the geometrical and physical settings, sometimes it is possible to associate, in a natural way, a length or magnitude and a direction to vectors. In turn, the notion of direction is strictly associated with the notion of an angle between two vectors. When the length of vectors is defined, it is possible to also define a dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

— a scalar-valued product of two vectors — which gives a convenient algebraic characterization of both length (the square root of the dot product of a vector by itself) and angle (a function of the dot product between any two vectors). In three dimensions, it is further possible to define a cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

which supplies an algebraic characterization of the area

Area

Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...

and orientation

Orientation (geometry)

In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....

in space of the parallelogram

Parallelogram

defined by two vectors (used as sides of the parallelogram).

However, it is not always possible or desirable to define the length of a vector in a natural way. This more general type of spatial vector is the subject of vector space

Vector space

s (for bound vectors) and affine space

Affine space

In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...

s (for free vectors). An important example is Minkowski space

Minkowski space

In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...

that is important to our understanding of special relativity

Special relativity

Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

, where there is a generalization of length that permits non-zero vectors to have zero length. Other physical examples come from thermodynamics

Thermodynamics

Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...

, where many of the quantities of interest can be considered vectors in a space with no notion of length or angle.

Generalizations

In physics, as well as mathematics, a vector is often identified with a tuple

Tuple

In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...

, or list of numbers, which depend on some auxiliary coordinate system or reference frame

Frame of reference

A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...

. When the coordinates are transformed, for example by rotation or stretching, then the components of the vector also transform. The vector itself has not changed, but the reference frame has, so the components of the vector (or measurements taken with respect to the reference frame) must change to compensate. The vector is called covariant or contravariant depending on how the transformation of the vector's components is related to the transformation of coordinates. In general, contravariant vectors are "regular vectors" with units of distance (such as a displacement) or distance times some other unit (such as velocity or acceleration); covariant vectors, on the other hand, have units of one-over-distance such as gradient

Gradient

In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....

. If you change units (a special case of a change of coordinates) from meters to milimeters, a scale factor of 1/1000, a displacement of 1 m becomes 1000 mm–a contravariant change in numerical value. In contrast, a gradient of 1 K

Kelvin

The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...

/m becomes 0.001 K/mm–a covariant change in value. See covariance and contravariance of vectors. Tensor

Tensor

s are another type of quantity that behave in this way; in fact a vector is a special type of tensor.

In pure mathematics

Mathematics

, a vector is any element of a vector space

Vector space

over some field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

and is often represented as a coordinate vector

Coordinate vector

In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....

. The vectors described in this article are a very special case of this general definition because they are contravariant with respect to the ambient space. Contravariance captures the physical intuition behind the idea that a vector has "magnitude and direction".

History

The concept of vector, as we know it today, evolved gradually over a period of more than 200 years. About a dozen people made significant contributions. The immediate predecessor of vectors were quaternions, devised by William Rowan Hamilton

William Rowan Hamilton

Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...

in 1843 as a generalization of complex numbers. His search was for a formalism to enable the analysis of three-dimensional space in the same way that complex numbers had enabled analysis of two-dimensional space. In 1846 Hamilton divided his quaternions into the sum of real and imaginary parts that he respectively called "scalar" and "vector":
Whereas complex numbers have one number

whose square is negative one, quaternions have three independent such numbers

. Multiplication of these numbers by each other is not commutative, e.g.,

. Multiplication of two quaternions yields a third quaternion whose scalar part is the negative of the modern dot product and whose vector part is the modern cross product.

Peter Guthrie Tait

Peter Guthrie Tait

Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...

carried the quaternion standard after Hamilton. His 1867 Elementary Treatise of Quaternions included extensive treatment of the nabla

Nabla symbol

right|thumb|256px|The [[harp]], the instrument after which the nabla symbol is namedNabla is the symbol \nabla . The name comes from the Greek word for a Hebrew harp, which had a similar shape. Related words also exist in Aramaic and Hebrew. The symbol was first used by William Rowan Hamilton in...

or del operator and is very close to modern vector analysis.

Josiah Willard Gibbs

Josiah Willard Gibbs

Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...

, who was exposed to quaternions through James Clerk Maxwell

James Clerk Maxwell

James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...

's Treatise on Electricity and Magnetism, separated off their vector part for independent treatment. The first half of Gibbs's Elements of Vector Analysis, published in 1881, presents what is essentially the modern system of vector analysis.

Representations

Vectors are usually denoted in lowercase boldface, as a or lowercase italic boldface, as a. (Uppercase letters are typically used to represent matrices

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

.) Other conventions include

or a, especially in handwriting. Alternatively, some use a tilde

Tilde

The tilde is a grapheme with several uses. The name of the character comes from Portuguese and Spanish, from the Latin titulus meaning "title" or "superscription", though the term "tilde" has evolved and now has a different meaning in linguistics....

(~) or a wavy underline drawn beneath the symbol, which is a convention for indicating boldface type. If the vector represents a directed distance

Distance

Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...

or displacement

Displacement (vector)

from a point A to a point B (see figure), it can also be denoted as

or AB.

Vectors are usually shown in graphs or other diagrams as arrows (directed line segment

Line segment

s), as illustrated in the figure. Here the point A is called the origin, tail, base, or initial point; point B is called the head, tip, endpoint, terminal point or final point. The length of the arrow is proportional to the vector's magnitude

Magnitude (mathematics)

, while the direction in which the arrow points indicates the vector's direction.

On a two-dimensional diagram, sometimes a vector perpendicular

Perpendicular

In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...

to the plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

of the diagram is desired. These vectors are commonly shown as small circles. A circle with a dot at its centre (Unicode U+2299 ⊙) indicates a vector pointing out of the front of the diagram, toward the viewer. A circle with a cross inscribed in it (Unicode U+2297 ⊗) indicates a vector pointing into and behind the diagram. These can be thought of as viewing the tip of an arrow head on and viewing the vanes of an arrow from the back.

In order to calculate with vectors, the graphical representation may be too cumbersome. Vectors in an n-dimensional Euclidean space can be represented in a Cartesian coordinate system

Cartesian coordinate system

. The endpoint of a vector can be identified with an ordered list of n real numbers (n-tuple

Tuple

). These numbers are the coordinates of the endpoint of the vector, with respect to a given Cartesian coordinate system

Cartesian coordinate system

, and are typically called the scalar components (or scalar projections) of the vector on the axes of the coordinate system.

As an example in two dimensions (see figure), the vector from the origin O = (0,0) to the point A = (2,3) is simply written as

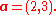
The notion that the tail of the vector coincides with the origin is implicit and easily understood. Thus, the more explicit notation

is usually not deemed necessary and very rarely used.

In three dimensional Euclidean space (or

), vectors are identified with triples of scalar components:

also written

These numbers are often arranged into a column vector or row vector, particularly when dealing with matrices

Matrix (mathematics)

, as follows:

Another way to represent a vector in n-dimensions is to introduce the standard basis

Standard basis

In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...

vectors. For instance, in three dimensions, there are three of them:

These have the intuitive interpretation as vectors of unit length pointing up the x, y, and z axis of a Cartesian coordinate system

Cartesian coordinate system

, respectively, and they are sometimes referred to as versors of those axes. In terms of these, any vector a in

can be expressed in the form:

where a₁, a₂, a₃ are called the vector components (or vector projections) of a on the basis vectors or, equivalently, on the corresponding Cartesian axes x, y, and z (see figure), while a₁, a₂, a₃ are the respective scalar components (or scalar projections).

In introductory physics textbooks, the standard basis vectors are often instead denoted

(or

, in which the hat symbol ^ typically denotes unit vectors). In this case, the scalar and vector components are denoted a_x, a_y, a_z, and a_x, a_y, a_z. Thus,

The notation e_i is compatible with the index notation

Index notation

Index notation is used in mathematics and computer programming to specify the elements of matrices or the components of a vector. The formalism of how indices are used varies according to the discipline...

and the summation convention commonly used in higher level mathematics, physics, and engineering.

Decomposition

As explained above a vector is often described by a set of vector components that are mutually perpendicular and add up to form the given vector. Typically, these components are the projections of the vector on a set of reference axes (or basis vectors). The vector is said to be decomposed or resolved with respect to that set.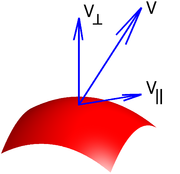

However, the decomposition of a vector into components is not unique, because it depends on the choice of the axes on which the vector is projected.

Moreover, the use of Cartesian versors such as

as a basis

Basis (linear algebra)

In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...

in which to represent a vector is not mandated. Vectors can also be expressed in terms of the versors of a Cylindrical coordinate system

Cylindrical coordinate system

A cylindrical coordinate system is a three-dimensional coordinate systemthat specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis...

(

) or Spherical coordinate system

Spherical coordinate system

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...

(

). The latter two choices are more convenient for solving problems which possess cylindrical or spherical symmetry respectively.

The choice of a coordinate system doesn't affect the properties of a vector or its behaviour under transformations.

A vector can be also decomposed with respect to "non-fixed" axes which change their orientation

Orientation (geometry)

In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....

as a function of time or space. For example, a vector in three dimensional space can be decomposed with respect to two axes, respectively normal, and tangent to a surface (see figure).
Moreover, the radial and tangential components of a vector relate to the radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

of rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...

of an object. The former is parallel

Parallel (geometry)

Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...

to the radius and the latter is orthogonal

Perpendicular

In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...

to it.

In these cases, each of the components may be in turn decomposed with respect to a fixed coordinate system or basis set (e.g., a global coordinate system, or inertial reference frame).

Basic properties

The following section uses the Cartesian coordinate system

Cartesian coordinate system

with basis vectors

and assume that all vectors have the origin as a common base point. A vector a will be written as

Equality

Two vectors are said to be equal if they have the same magnitude and direction. Equivalently they will be equal if their coordinates are equal. So two vectors

and

are equal if

Addition and subtraction

Assume now that a and b are not necessarily equal vectors, but that they may have different magnitudes and directions. The sum of a and b is

The addition may be represented graphically by placing the start of the arrow b at the tip of the arrow a, and then drawing an arrow from the start of a to the tip of b. The new arrow drawn represents the vector a + b, as illustrated below:

This addition method is sometimes called the parallelogram rule because a and b form the sides of a parallelogram

Parallelogram

and a + b is one of the diagonals. If a and b are bound vectors that have the same base point, it will also be the base point of a + b. One can check geometrically that a + b = b + a and (a + b) + c = a + (b + c).

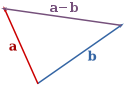
The difference of a and b is

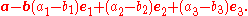
Subtraction of two vectors can be geometrically defined as follows: to subtract b from a, place the end points of a and b at the same point, and then draw an arrow from the tip of b to the tip of a. That arrow represents the vector a − b, as illustrated below:

Scalar multiplication

A vector may also be multiplied, or re-scaled, by a real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

r. In the context of conventional vector algebra, these real numbers are often called scalars (from scale) to distinguish them from vectors. The operation of multiplying a vector by a scalar is called scalar multiplication. The resulting vector is

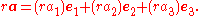
Intuitively, multiplying by a scalar r stretches a vector out by a factor of r. Geometrically, this can be visualized (at least in the case when r is an integer) as placing r copies of the vector in a line where the endpoint of one vector is the initial point of the next vector.

If r is negative, then the vector changes direction: it flips around by an angle of 180°. Two examples (r = −1 and r = 2) are given below:

Scalar multiplication is distributive

Distributivity

In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...

over vector addition in the following sense: r(a + b) = ra + rb for all vectors a and b and all scalars r. One can also show that a − b = a + (−1)b.

Length

The length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...

or magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....

or norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...

of the vector a is denoted by ||a|| or, less commonly, |a|, which is not to be confused with the absolute value

Absolute value

In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

(a scalar "norm").

The length of the vector a can be computed with the Euclidean norm

which is a consequence of the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

since the basis vectors e₁, e₂, e₃ are orthogonal unit vectors.

This happens to be equal to the square root of the dot product

Dot product

, discussed below, of the vector with itself:

Unit vector

A unit vector is any vector with a length of one; normally unit vectors are used simply to indicate direction. A vector of arbitrary length can be divided by its length to create a unit vector. This is known as normalizing a vector. A unit vector is often indicated with a hat as in â.

To normalize a vector a = [a₁, a₂, a₃], scale the vector by the reciprocal of its length ||a||. That is:

Null vector
The null vector (or zero vector) is the vector with length zero. Written out in coordinates, the vector is (0,0,0), and it is commonly denoted

, or 0, or simply 0. Unlike any other vector it has an arbitrary or indeterminate direction, and cannot be normalized (that is, there is no unit vector which is a multiple of the null vector). The sum of the null vector with any vector a is a (that is, 0+a=a).

Dot product

The dot product of two vectors a and b (sometimes called the inner product
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...

, or, since its result is a scalar, the scalar product) is denoted by a ∙ b and is defined as:

where θ is the measure of the angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

between a and b (see trigonometric function

Trigonometric function

In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...

for an explanation of cosine). Geometrically, this means that a and b are drawn with a common start point and then the length of a is multiplied with the length of that component of b that points in the same direction as a.

The dot product can also be defined as the sum of the products of the components of each vector as

Cross product

The cross product (also called the vector product or outer product) is only meaningful in three or seven dimensions. The cross product differs from the dot product primarily in that the result of the cross product of two vectors is a vector. The cross product, denoted a × b, is a vector perpendicular to both a and b and is defined as

where θ is the measure of the angle between a and b, and n is a unit vector perpendicular

Perpendicular

In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...

to both a and b which completes a right-handed system. The right-handedness constraint is necessary because there exist two unit vectors that are perpendicular to both a and b, namely, n and (–n).

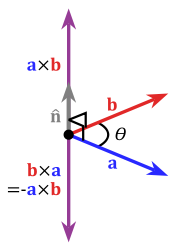
The cross product a × b is defined so that a, b, and a × b also becomes a right-handed system (but note that a and b are not necessarily orthogonal). This is the right-hand rule

Right-hand rule

In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....

.

The length of a × b can be interpreted as the area of the parallelogram having a and b as sides.

The cross product can be written as

For arbitrary choices of spatial orientation (that is, allowing for left-handed as well as right-handed coordinate systems) the cross product of two vectors is a pseudovector

Pseudovector

instead of a vector (see below).

Scalar triple product

The scalar triple product (also called the box product or mixed triple product) is not really a new operator, but a way of applying the other two multiplication operators to three vectors. The scalar triple product is sometimes denoted by (a b c) and defined as:

It has three primary uses. First, the absolute value of the box product is the volume of the parallelepiped

Parallelepiped

In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...

which has edges that are defined by the three vectors. Second, the scalar triple product is zero if and only if the three vectors are linearly dependent

Linear independence

In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...

, which can be easily proved by considering that in order for the three vectors to not make a volume, they must all lie in the same plane. Third, the box product is positive if and only if the three vectors a, b and c are right-handed.

In components (with respect to a right-handed orthonormal basis), if the three vectors are thought of as rows (or columns, but in the same order), the scalar triple product is simply the determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

of the 3-by-3 matrix

Matrix (mathematics)

having the three vectors as rows

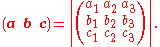
The scalar triple product is linear in all three entries and anti-symmetric in the following sense:

Multiple Cartesian bases

All examples thus far have dealt with vectors expressed in terms of the same basis, namely, e₁,e₂,e₃. However, a vector can be expressed in terms of any number of different bases that are not necessarily aligned with each other, and still remain the same vector. For example, using the vector a from above,

where n₁,n₂,n₃ form another orthonormal basis not aligned with e₁,e₂,e₃. The values of u, v, and w are such that the resulting vector sum is exactly a.

It is not uncommon to encounter vectors known in terms of different bases (for example, one basis fixed to the Earth and a second basis fixed to a moving vehicle). In order to perform many of the operations defined above, it is necessary to know the vectors in terms of the same basis. One simple way to express a vector known in one basis in terms of another uses column matrices that represent the vector in each basis along with a third matrix containing the information that relates the two bases. For example, in order to find the values of u, v, and w that define a in the n₁,n₂,n₃ basis, a matrix multiplication may be employed in the form

where each matrix element c_jk is the direction cosine relating n_j to e_k. The term direction cosine refers to the cosine of the angle between two unit vectors, which is also equal to their dot product.

By referring collectively to e₁,e₂,e₃ as the e basis and to n₁,n₂,n₃ as the n basis, the matrix containing all the c_jk is known as the "transformation matrix from e to n", or the "rotation matrix from e to n" (because it can be imagined as the "rotation" of a vector from one basis to another), or the "direction cosine matrix from e to n" (because it contains direction cosines).

The properties of a rotation matrix are such that its inverse is equal to its transpose. This means that the "rotation matrix from e to n" is the transpose of "rotation matrix from n to e".

By applying several matrix multiplications in succession, any vector can be expressed in any basis so long as the set of direction cosines is known relating the successive bases.

Other dimensions

With the exception of the cross and triple products, the above formula generalise to two dimensions and higher dimensions. For example, addition generalises to two dimensions the addition of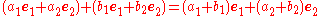

and in four dimension

The cross product generalises to the exterior product, whose result is a bivector

Bivector

In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...

, which in general is not a vector. In two dimensions this is simply a scalar

The seven-dimensional cross product is similar to the cross product in that its result is a seven-dimensional vector orthogonal to the two arguments.

Length and units

In abstract vector spaces, the length of the arrow depends on a dimensionless scale. If it represents, for example, a force, the "scale" is of physical dimension

Dimensional analysis

In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...

length/force. Thus there is typically consistency in scale among quantities of the same dimension, but otherwise scale ratios may vary; for example, if "1 newton" and "5 m" are both represented with an arrow of 2 cm, the scales are 1:250 and 1 m:50 N respectively. Equal length of vectors of different dimension has no particular significance unless there is some proportionality constant inherent in the system that the diagram represents. Also length of a unit vector (of dimension length, not length/force, etc.) has no coordinate-system-invariant significance.

Vector-valued functions

Often in areas of physics and mathematics, a vector evolves in time, meaning that it depends on a time parameter t. For instance, if r represents the position vector of a particle, then r(t) gives a parametric

Parametric equation

In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....

representation of the trajectory of the particle. Vector-valued functions can be differentiated

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

and integrated

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

by differentiating or integrating the components of the vector, and many of the familiar rules from calculus

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

continue to hold for the derivative and integral of vector-valued functions.

Position, velocity and acceleration

The position of a point x=(x₁, x₂, x₃) in three dimensional space can be represented as a position vector whose base point is the origin

The position vectors has dimensions of length

Length

In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...

.

Given two points x=(x₁, x₂, x₃), y=(y₁, y₂, y₃) their displacement

Displacement (vector)

is a vector

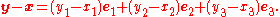
which specifies the position of y relative to x. The length of this vector gives the straight line distance from x to y. Displacement has the dimensions of length.

The velocity

Velocity

v of a point or particle is a vector, its length gives the speed

Speed

. For constant velocity the position at time t will be

where x₀ is the position at time t=0. Velocity is the time derivative of position. Its dimensions are length/time.

Acceleration

Acceleration

a of a point is vector which is the time derivative of velocity. Its dimensions are length/time².

Force, energy, work

Force

is a vector with dimensions of mass×length/time² and Newton's second law is the scalar multiplication

Work is the dot product of force

Force

and displacement

Displacement (vector)

Vectors as directional derivatives

A vector may also be defined as a directional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...

: consider a function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

and a curve

. Then the directional derivative of

is a scalar defined as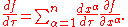

where the index

is summed over the appropriate number of dimensions (for example, from 1 to 3 in 3-dimensional Euclidean space, from 0 to 3 in 4-dimensional spacetime, etc.). Then consider a vector tangent to

The directional derivative can be rewritten in differential form (without a given function

) as

Therefore any directional derivative can be identified with a corresponding vector, and any vector can be identified with a corresponding directional derivative. A vector can therefore be defined precisely as

Vectors, pseudovectors, and transformations

An alternative characterization of Euclidean vectors, especially in physics, describes them as lists of quantities which behave in a certain way under a coordinate transformation

Coordinate system

. A contravariant vector is required to have components that "transform like the coordinates" under changes of coordinates such as rotation

Rotation (mathematics)

In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...

and dilation. The vector itself does not change under these operations; instead, the components of the vector make a change that cancels the change in the spatial axes, in the same way that co-ordinates change. In other words, if the reference axes were rotated in one direction, the component representation of the vector would rotate in exactly the opposite way. Similarly, if the reference axes were stretched in one direction, the components of the vector, like the co-ordinates, would reduce in an exactly compensating way. Mathematically, if the coordinate system undergoes a transformation described by an invertible matrix M, so that a coordinate vector x is transformed to x′ = Mx, then a contravariant vector v must be similarly transformed via v′ = Mv. This important requirement is what distinguishes a contravariant vector from any other triple of physically meaningful quantities. For example, if v consists of the x, y, and z-components of velocity

Velocity

, then v is a contravariant vector: if the coordinates of space are stretched, rotated, or twisted, then the components of the velocity transform in the same way. On the other hand, for instance, a triple consisting of the length, width, and height of a rectangular box could make up the three components of an abstract vector

Vector space

, but this vector would not be contravariant, since rotating the box does not change the box's length, width, and height. Examples of contravariant vectors include displacement

Displacement (vector)

, velocity

Velocity

, electric field

Electric field

, momentum

Momentum

In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...

, force

Force

, and acceleration

Acceleration

.

In the language of differential geometry, the requirement that the components of a vector transform according to the same matrix of the coordinate transition is equivalent to defining a contravariant vector to be a tensor

Tensor

of contravariant rank one. Alternatively, a contravariant vector is defined to be a tangent vector

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

, and the rules for transforming a contravariant vector follow from the chain rule

Chain rule

In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...

.

Some vectors transform like contravariant vectors, except that when they are reflected through a mirror, they flip and gain a minus sign. A transformation that switches right-handedness to left-handedness and vice versa like a mirror does is said to change the orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...

of space. A vector which gains a minus sign when the orientation of space changes is called a pseudovector
Pseudovector
In physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...

or an axial vector. Ordinary vectors are sometimes called true vectors or polar vectors to distinguish them from pseudovectors. Pseudovectors occur most frequently as the cross product

Cross product

of two ordinary vectors.

One example of a pseudovector is angular velocity

Angular velocity

In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...

. Driving in a car

Čar

Čar is a village in the municipality of Bujanovac, Serbia. According to the 2002 census, the town has a population of 296 people.-References:...

, and looking forward, each of the wheel

Wheel

A wheel is a device that allows heavy objects to be moved easily through rotating on an axle through its center, facilitating movement or transportation while supporting a load, or performing labor in machines. Common examples found in transport applications. A wheel, together with an axle,...

s has an angular velocity vector pointing to the left. If the world is reflected in a mirror which switches the left and right side of the car, the reflection of this angular velocity vector points to the right, but the actual angular velocity vector of the wheel still points to the left, corresponding to the minus sign. Other examples of pseudovectors include magnetic field

Magnetic field

, torque

Torque

Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....

, or more generally any cross product of two (true) vectors.

This distinction between vectors and pseudovectors is often ignored, but it becomes important in studying symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

properties. See parity (physics)

Parity (physics)

In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...

External links

Online vector identities (PDF
Portable Document Format
Portable Document Format is an open standard for document exchange. This file format, created by Adobe Systems in 1993, is used for representing documents in a manner independent of application software, hardware, and operating systems....

)
Introducing Vectors A conceptual introduction (applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...

)
Addition of forces (vectors) Java Applet
French tutorials on vectors and their application to video games

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Overview

Examples in one dimension

In physics and engineering

In Cartesian space

Euclidean and affine vectors

Generalizations

History

Representations

Decomposition

Basic properties

Equality

Addition and subtraction

Scalar multiplication

Length

Dot product

Cross product

Scalar triple product

Multiple Cartesian bases

Other dimensions

Length and units

Vector-valued functions

Position, velocity and acceleration

Force, energy, work

Vectors as directional derivatives

Vectors, pseudovectors, and transformations

See also

External links