
List of nonlinear partial differential equations
Encyclopedia
In mathematics and physics, nonlinear partial differential equations are (as their name suggests) partial differential equations with nonlinear terms. They describe many different physical systems, ranging from gravitation to fluid dynamics, and have been used in mathematics to solve problems such as the Poincaré conjecture
and the Calabi conjecture
. They are difficult to study: there are almost no general techniques that work for all such equations, and usually each individual equation has to be studied as a separate problem.
.
s.
An example of singularity formation is given by the Ricci flow
: Hamilton showed that while short time solutions exist, singularities will usually form after a finite time. Perelman's solution of the Poincaré conjecture
depended on a deep study of these singularities, where he showed how to continue the solution past the singularities.
for some very special PDEs this is possible. (In general this is a hopeless problem: it is unlikely that there is any useful description of all solutions of the Navier–Stokes equation for example, as this would involve describing all possible fluid motions.) If the equation has a very large symmetry group, then one is usually only interested in the moduli space of solutions modulo the symmetry group, and this is sometimes a finite dimensional compact manifold, possibly with singularities; for example, this happens in the case of the Seiberg-Witten equations. A slightly more complicated case is the self dual Yang-Mills equations, when the moduli space is finite dimensional but not necessarily compact, though it can often be compactified explicitly. Another case when one can sometimes hope to describe all solutions is the case of completely integrable models, when solutions are sometimes a sort of superposition of solitons; for example, this happens for the Korteweg–de Vries equation
.
, or by looking for highly symmetric solutions.
Some equations have several different exact solutions.
form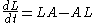
then it usually has an infinite number of first integrals, which help to study it.
s for a variational problem. Systems of this form can sometimes be solved by finding an extremum of the original variational problem.
.
) are invariant under diffeomorphisms of the underlying manifold. Any such symmetry groups can usually be used to help study the equations; in particular if one solution is known one can trivially generate more by acting with the symmetry group.
Sometimes equations are parabolic or hyperbolic "modulo the action of some group": for example, the Ricci flow
equation is not quite parabolic, but is "parabolic modulo the action of the diffeomorphism group", which implies that it has most of the good properties of parabolic equations.
and the tables below.
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
and the Calabi conjecture
Calabi conjecture
In mathematics, the Calabi conjecture was a conjecture about the existence of good Riemannian metrics on complex manifolds, made by and proved by ....
. They are difficult to study: there are almost no general techniques that work for all such equations, and usually each individual equation has to be studied as a separate problem.
Existence and uniqueness of solutions
A fundamental question for any PDE is the existence and uniqueness of a solution for given boundary conditions. For nonlinear equations these questions are in general very hard: for example, the hardest part of Yau's solution of the Calabi conjecture was the proof of existence for a Monge-Ampere equationMonge-Ampère equation
In mathematics, a Monge–Ampère equation is a nonlinear second order partial differential equation of special kind. A second order equation for the unknown function u of two variables x,y is of Monge–Ampère type if it is linear in the determinant of the Hessian matrix of u and in the second order...
.
Singularities
The basic questions about singularities (their formation, propagation, and removal, and regularity of solutions) are the same as for linear PDE, but as usual much harder to study. In the linear case one can just use spaces of distributions, but nonlinear PDEs are not usually defined on arbitrary distributions, so one replaces spaces of distributions by refinements such as Sobolev spaceSobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s.
An example of singularity formation is given by the Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
: Hamilton showed that while short time solutions exist, singularities will usually form after a finite time. Perelman's solution of the Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
depended on a deep study of these singularities, where he showed how to continue the solution past the singularities.
Linear approximation
The solutions in a neighborhood of a known solution can sometimes be studied by linearizing the PDE around the solution. This corresponds to studying the tangent space of a point of the moduli space of all solutions.Moduli space of solutions
Ideally one would like to describe the (moduli) space of all solutions explicitly, andfor some very special PDEs this is possible. (In general this is a hopeless problem: it is unlikely that there is any useful description of all solutions of the Navier–Stokes equation for example, as this would involve describing all possible fluid motions.) If the equation has a very large symmetry group, then one is usually only interested in the moduli space of solutions modulo the symmetry group, and this is sometimes a finite dimensional compact manifold, possibly with singularities; for example, this happens in the case of the Seiberg-Witten equations. A slightly more complicated case is the self dual Yang-Mills equations, when the moduli space is finite dimensional but not necessarily compact, though it can often be compactified explicitly. Another case when one can sometimes hope to describe all solutions is the case of completely integrable models, when solutions are sometimes a sort of superposition of solitons; for example, this happens for the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
.
Exact solutions
It is often possible to write down some special solutions explicitly in terms of elementary functions (though it is rarely possible to describe all solutions like this). One way of finding such explicit solutions is to reduce the equations to equations of lower dimension, preferably ordinary differential equations, which can often be solved exactly. This can sometimes be done using separation of variablesSeparation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
, or by looking for highly symmetric solutions.
Some equations have several different exact solutions.
Numerical solutions
Numerical solution on a computer is almost the only method that can be used for getting information about arbitrary systems of PDEs. There has been a lot of work done on solving certain systems numerically, especially for the Navier–Stokes and other equations related to weather prediction.Lax pair
If a system of PDEs can be put into Lax pairLax pair
In mathematics, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that describe the corresponding differential equations. They were introduced by Peter Lax to discuss solitons in continuous media...
form
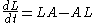
then it usually has an infinite number of first integrals, which help to study it.
Euler-Lagrange equations
Systems of PDEs often arise as the Euler-Lagrange equationEuler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
s for a variational problem. Systems of this form can sometimes be solved by finding an extremum of the original variational problem.
Integrable systems
PDEs that arise from integrable systems are often the easiest to study, and can sometimes be completely solved. A well known example is the Korteweg–de Vries equationKorteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
.
Symmetry
Some systems of PDEs have large symmetry groups. For example, the Yang-Mills equations are invariant under an infinite dimensional gauge group, and many systems of equations (such as the Einstein field equationsEinstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
) are invariant under diffeomorphisms of the underlying manifold. Any such symmetry groups can usually be used to help study the equations; in particular if one solution is known one can trivially generate more by acting with the symmetry group.
Sometimes equations are parabolic or hyperbolic "modulo the action of some group": for example, the Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
equation is not quite parabolic, but is "parabolic modulo the action of the diffeomorphism group", which implies that it has most of the good properties of parabolic equations.
Look it up
There are several tables of previously studied PDEs such as andand the tables below.
A–F
| Name | Dim | Equation | Applications |
|---|---|---|---|
| Benjamin–Bona–Mahony | 1+1 | 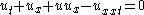 |
Fluid mechanics |
| Benjamin-Ono | 1+1 | 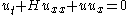 |
internal waves in deep water |
| Boomeron | 1+1 | 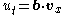 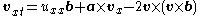 |
Soliton Soliton In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium... s |
| Born-Infeld | 1+1 | 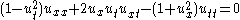 |
|
| Boussinesq | 1+1 | 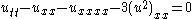 |
Fluid mechanics |
| Buckmaster | 1+1 | 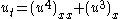 |
Thin viscous fluid sheet flow |
| Burgers Burgers' equation Burgers' equation is a fundamental partial differential equation from fluid mechanics. It occurs in various areas of applied mathematics, such as modeling of gas dynamics and traffic flow... |
1+1 |  |
Fluid mechanics |
| Cahn-Hilliard equation | Any |  |
Phase separation |
| Calabi flow Calabi flow In differential geometry, the Calabi flow is an intrinsic geometric flow—a process which deforms the metric of a Riemannian manifold—in a manner formally analogous to the way that vibrations are damped and dissipated in a hypothetical curved n-dimensional structural element.The Calabi flow is an... |
Any | Calabi-Yau manifold Calabi-Yau manifold A Calabi-Yau manifold is a special type of manifold that shows up in certain branches of mathematics such as algebraic geometry, as well as in theoretical physics... s |
|
| Camassa–Holm | 1+1 | 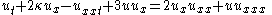 |
Peakons |
| Carleman | 1+1 |  |
|
| Cauchy momentum | any |  |
Momentum transport |
| Caudrey-Dodd-Gibbon- Sawada-Kotera | 1+1 | Same as (rescaled) Sawada-Kotera | |
| Chiral field | 1+1 | ||
| Clairaut equation | any | 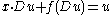 |
Differential geometry |
| Complex Monge-Ampère | Any | 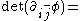 lower order terms lower order terms |
Calabi conjecture Calabi conjecture In mathematics, the Calabi conjecture was a conjecture about the existence of good Riemannian metrics on complex manifolds, made by and proved by .... |
| Davey–Stewartson Davey–Stewartson equation In fluid dynamics, the Davey–Stewartson equation was introduced in a paper by to describe the evolution of a three-dimensional wave-packet on water of finite depth.... |
1+2 |  |
Finite depth waves |
| Degasperis-Procesi | 1+1 | 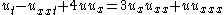 |
Peakons |
| Dispersive long wave | 1+1 |  , , 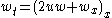 |
|
| Drinfel'd -Sokolov -Wilson | 1+1 | 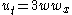 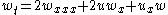 |
|
| Dym equation | 1+1 | 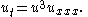 |
Soliton Soliton In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium... s |
| Eckhaus equation | 1+1 | Integrable systems | |
| Eikonal equation Eikonal equation The eikonal equation is a non-linear partial differential equation encountered in problems of wave propagation, when the wave equation is approximated using the WKB theory... |
any | optics | |
| Einstein field equations Einstein field equations The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy... |
Any | 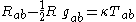 |
General relativity General relativity General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics... |
| Ernst equation Ernst equation In mathematics, the Ernst equation is the non-linear partial differential equation\displaystyle \Re = ^2+^2.It is used to produce exact solutions of Einstein's equations.... |
2 |  |
|
| Euler equations Euler equations In fluid dynamics, the Euler equations are a set of equations governing inviscid flow. They are named after Leonhard Euler. The equations represent conservation of mass , momentum, and energy, corresponding to the Navier–Stokes equations with zero viscosity and heat conduction terms. Historically,... |
1+3 | 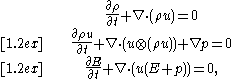 |
non-viscous fluids |
| Fisher's equation Fisher's equation In mathematics, Fisher's equation, also known as the Fisher-Kolmogorov equation and the Fisher-KPP equation, named after R. A. Fisher and A. N... |
1+1 | 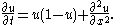 |
Gene propagation |
| Fitzhugh-Nagumo FitzHugh–Nagumo model The FitzHugh–Nagumo model, named after Richard FitzHugh who suggested the system in 1961 and J. Nagumo et al. who created the equivalent circuit the following year, describes a prototype of an excitable system .... |
1+1 | 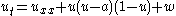 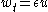 |
G–K
| Name | Dim | Equation | Applications |
|---|---|---|---|
| Gardner equation | 1+1 | 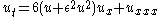 |
|
| Garnier equation | isomonodromic deformations | ||
| Gauss-Codazzi | surfaces | ||
| Ginzburg-Landau | 1+3 | Superconductivity | |
| Gross-Neveu Gross-Neveu model The Gross-Neveu model is a quantum field theory model of Dirac fermions interacting via four fermion interactions in 1 spatial and 1 time dimension. It was introduced in 1974 by David Gross and André Neveu as a toy model for quantum chromodynamics, the theory of strong interactions.It consists of... |
1+1 | ||
| Gross –Pitaevskii Gross-Pitaevskii equation The Gross–Pitaevskii equation describes the ground state of a quantum system of identical bosons using the Hartree–Fock approximation and the pseudopotential interaction model.... |
1+n | Bose–Einstein condensate Bose–Einstein condensate A Bose–Einstein condensate is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near absolute zero . Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at... |
|
| Hartree equation | Any | where 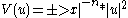 . . |
|
| Hasegawa-Mima Hasegawa-Mima equation In plasma physics, the Hasegawa–Mima equation, named after Akira Hasegawa and Kunioki Mima, is an equation that describes a certain regime of plasma, where the time scales are very fast, and the distance scale in the direction of the magnetic field is long. In particular the equation is useful for... |
1+3 | 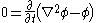 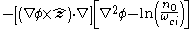 |
Turbulence in plasma |
| Heisenberg ferromagnet | 1+1 | 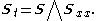 |
Magnetism |
| Hirota equation | 1+1 | ||
| Hirota -Satsuma | 1+1 | 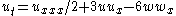 , ,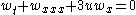 |
|
| Hunter–Saxton | 1+1 | 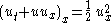 |
Liquid crystal Liquid crystal Liquid crystals are a state of matter that have properties between those of a conventional liquid and those of a solid crystal. For instance, an LC may flow like a liquid, but its molecules may be oriented in a crystal-like way. There are many different types of LC phases, which can be... s |
| Ishimori equation Ishimori equation The Ishimori equation is a partial differential equation proposed by the Japanese mathematician . Its interest is as the first example of a nonlinear spin-one field model in the plane that is integrable .-Equation:The IE has the form... |
1+2 | 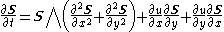  |
Integrable systems |
| Kadomtsev –Petviashvili | 1+2 | 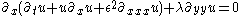 |
Shallow water waves |
| von Karman | 2 |  , , 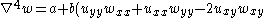 |
|
| Kaup | 1+1 | 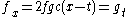 |
|
| Kaup –Kupershmidt | 1+1 | 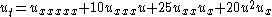 |
Integrable systems |
| Klein -Gordon -Maxwell | any | , 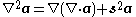 |
|
| Klein -Gordon (nonlinear) | any | 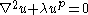 |
|
| Klein -Gordon -Zakharov | |||
| Khokhlov -Zabolotskaya | 1+2 |  |
|
| Korteweg–de Vries Korteweg–de Vries equation In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified... (KdV) |
1+1 | 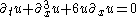 |
Shallow waves, Integrable systems |
| KdV (generalized) Generalized Korteweg-de Vries equation In mathematics the generalized Korteweg-de Vries equation is the nonlinear partial differential equation\partial_t u + \partial_x^3 u + \partial_x f = 0.\,The function f... |
1+1 | 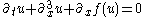 |
|
| KdV (modified) Korteweg–de Vries equation In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified... |
1+1 |  |
|
| KdV (super) | 1+1 | 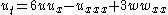 , , 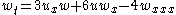 |
|
| There are more minor variations listed in the article on KdV equations. | |||
| Kuramoto -Sivashinsky | 1+n | ||
L–R
| Name | Dim | Equation | Applications |
|---|---|---|---|
| Landau–Lifshitz model Landau–Lifshitz model In solid-state physics, the Landau–Lifshitz equation , named for Lev Landau and Evgeny Lifshitz, is a partial differential equation describing time evolution of magnetism in solids, depending on 1 time variable and 1, 2, or 3 space variables.... |
1+n |  |
Magnetic field in solids |
| Lin-Tsien equation Lin-Tsien equation The Lin–Tsien equation is the partial differential equation- References :* D. Zwillinger. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 138, 1997.... |
1+2 |  |
|
| Liouville | any |  |
|
| Minimal surface | 3 | minimal surface Minimal surface In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints.... s |
|
| Molenbroeck | 2 | ||
| Monge–Ampère | any |  lower order terms lower order terms |
|
| Navier–Stokes(and its derivation) Derivation of the Navier–Stokes equations The intent of this article is to highlight the important points of the derivation of the Navier–Stokes equations as well as the application and formulation for different families of fluids.-Basic assumptions:... |
1+3 | 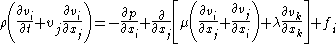 + mass conservation: 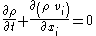 + an equation of state Equation of state In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions... to relate p and ρ, e.g. for an incompressible flow Incompressible flow In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid... :  |
Fluid flow |
| Nonlinear Schrödinger (cubic) Nonlinear Schrödinger equation In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state... |
1+1 | optics, water waves | |
| Nonlinear Schrödinger (derivative) Nonlinear Schrödinger equation In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state... |
1+1 | optics, water waves | |
| Novikov–Veselov equation Novikov–Veselov equation In mathematics, the Novikov–Veselov equation is a natural -dimensional analogue of the Korteweg–de Vries equation. Unlike another -dimensional analogue of KdV, the Kadomtsev–Petviashvili equation, it is integrable via the inverse scattering transform for the 2-dimensional stationary Schrödinger... |
1+2 | see Veselov–Novikov equation below | |
| Omega equation | 1+3 | 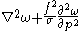 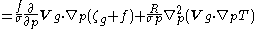 |
atmospheric physics |
| Plateau | 2 | 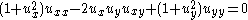 |
|
| Pohlmeyer -Lund -Regge | 2 |   |
|
| Porous medium | 1+n | 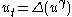 |
diffusion |
| Prandtl | 1+2 |  , , 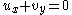 |
boundary layer |
| Primitive equations Primitive equations The primitive equations are a set of nonlinear differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models... |
1+3 | Atmospheric models |
S–Z, α–ω
| Name | Dim | Equation | Applications |
|---|---|---|---|
| Rayleigh | 2 | 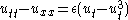 |
|
| Ricci flow Ricci flow In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric.... |
Any | 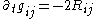 |
Poincaré conjecture Poincaré conjecture In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space... |
| Richards equation Richards equation The Richards equation represents the movement of water in unsaturated soils, and was formulated by Lorenzo A. Richards in 1931 . It is a non-linear partial differential equation, which is often difficult to approximate since it does not have a closed-form analytical solution.Darcy's law was... |
1+3 | 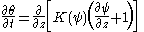 |
Variably-saturated flow in porous media |
| Sawada-Kotera | 1+1 | 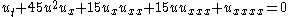 |
|
| Schlesinger | Any | 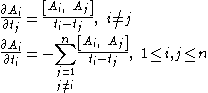 |
isomonodromic deformations |
| Seiberg-Witten | 1+3 |  |
Seiberg-Witten invariants, QFT Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... |
| Shallow water Shallow water equations The shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid .The equations are derived from depth-integrating the Navier–Stokes... |
1+2 | 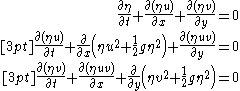 |
shallow water waves |
| Sine-Gordon Sine-Gordon equation The sine–Gordon equation is a nonlinear hyperbolic partial differential equation in 1 + 1 dimensions involving the d'Alembert operator and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative... |
1+1 | 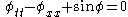 |
Soliton Soliton In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium... s, QFT Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... |
| Sinh-Gordon | 1+1 | 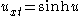 |
Soliton Soliton In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium... s, QFT Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... |
| Sinh-poisson | 1+n | 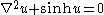 |
|
| Swift-Hohenberg Swift-Hohenberg equation The Swift–Hohenberg equation is a partial differential equation noted for its pattern-forming behaviour... |
any | 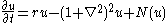 |
pattern forming |
| Three-wave equation | 1+n | Integrable systems | |
| Thomas equation | 2 | 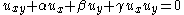 |
|
| Thirring model Thirring model The Thirring model is an exactly solvable quantum field theory which describes the self-interactions of a Dirac field in two dimension.-Definition:The Thirring model is given by the Lagrangian density... |
1+1 | , 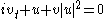 |
Dirac field, QFT Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... |
| Toda lattice | any | 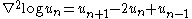 |
|
| Veselov–Novikov equation Novikov–Veselov equation In mathematics, the Novikov–Veselov equation is a natural -dimensional analogue of the Korteweg–de Vries equation. Unlike another -dimensional analogue of KdV, the Kadomtsev–Petviashvili equation, it is integrable via the inverse scattering transform for the 2-dimensional stationary Schrödinger... |
1+2 | 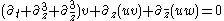 , , 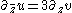 , , 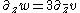 |
shallow water waves |
| Wadati- Konno- Ichikawa- Schimizu | 1+1 | ||
| WDVV equations | Any | 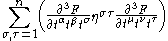 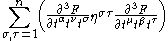 |
Topological field theory, QFT Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... |
| WZW model | 1+1 | QFT Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... |
|
| Witham equation | phase averaging | ||
| Yamabe Yamabe problem The Yamabe problem in differential geometry concerns the existence of Riemannian metrics with constant scalar curvature, and takes its name from the mathematician Hidehiko Yamabe. Although claimed to have a solution in 1960, a critical error... |
n | 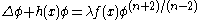 |
Differential geometry |
| Yang-Mills equation (source-free) | Any | 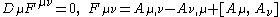 |
Gauge theory Gauge theory In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory... , QFT Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... |
| Yang-Mills (self-dual/anti-self-dual) Instanton An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory... |
4 | 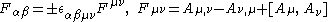 |
Instantons, Donaldson theory Donaldson theory Donaldson theory is the study of smooth 4-manifolds using gauge theory. It was started by Simon Donaldson who proved Donaldson's theorem restricting the possible quadratic forms on the second cohomology group of a compact simply connected 4-manifold.... , QFT Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... |
| Yukawa equation | 1+n | 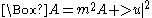 |
Meson Meson In particle physics, mesons are subatomic particles composed of one quark and one antiquark, bound together by the strong interaction. Because mesons are composed of sub-particles, they have a physical size, with a radius roughly one femtometer: 10−15 m, which is about the size of a proton... -nucleon Nucleon In physics, a nucleon is a collective name for two particles: the neutron and the proton. These are the two constituents of the atomic nucleus. Until the 1960s, the nucleons were thought to be elementary particles... interactions, QFT Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... |
| Zakharov system | 1+3 |  |
Langmuir waves |
| Zakharov–Schulman Zakharov–Schulman system In mathematics, the Zakharov–Schulman system is a system of nonlinear partial differential equations introduced in to describe the interactions of small amplitude, high frequency waves with acoustic waves.... |
1+3 | 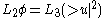 |
Acoustic waves |
| Zoomeron | 1+1 | 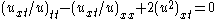 |
Soliton Soliton In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium... s |
| φ4 equation | 1+1 | 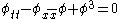 |
QFT Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... |
| σ-model Non-linear sigma model In quantum field theory, a nonlinear σ model describes a scalar field Σ which takes on values in a nonlinear manifold called the target manifold T.... |
1+1 | 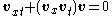 |
Harmonic maps, integrable systems, QFT Quantum field theory Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and... |
See also
- Euler-Lagrange equationEuler-Lagrange equationIn calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
- Nonlinear system
- Integrable systemIntegrable systemIn mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
- Inverse scattering transformInverse scattering transformIn mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
- Dispersive partial differential equationDispersive partial differential equationIn mathematics, a dispersive partial differential equation or dispersive PDE is a partial differential equation that is dispersive. In this context, dispersion means that waves of different wavelength propagate at different phase velocities....

