Limits

Limit (mathematics)

In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...

• Limit of a sequence
  Limit of a sequence
  The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
  
  
  • Subsequential limit
    Subsequential limit
    In mathematics, a subsequential limit of a sequence is the limit of some subsequence. Every subsequential limit is a cluster point, but not conversely. In first-countable spaces, the two concepts coincide....
    
     - the limit of some subsequence
• Limit of a function
  Limit of a function
  In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
  
   (see List of limits for a list of limits of common functions)
  • One-sided limit
    One-sided limit
    In calculus, a one-sided limit is either of the two limits of a function f of a real variable x as x approaches a specified point either from below or from above...
    
     - either of the two limits of functions of real variables x, as x approaches a point from above or below
  • Squeeze theorem
    Squeeze theorem
    In calculus, the squeeze theorem is a theorem regarding the limit of a function....
    
     - confirms the limit of a function via comparison with two other functions
  • Big O notation
    Big O notation
    In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
    
     - used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions

Sequence

Sequence

In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...

s and Series

Series (mathematics)

A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....

• Arithmetic progression
  Arithmetic progression
  In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
  
   - a sequence of numbers such that the difference between the consecutive terms is constant
  • Generalized arithmetic progression
    Generalized arithmetic progression
    In mathematics, a multiple arithmetic progression, generalized arithmetic progression, or k-dimensional arithmetic progression, is a set of integers constructed as an arithmetic progression is, but allowing several possible differences. So, for example, we start at 17 and may add a multiple of 3 or...
    
     - a sequence of numbers such that the difference between consecutive terms can be one of several possible constants
• Geometric progression
  Geometric progression
  In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
  
   - a sequence of numbers such that each consecutive term is found by multiplying the previous one by a fixed non-zero number
• Harmonic progression - a sequence formed by taking the reciprocals of the terms of an arithmetic progression
• Finite sequence - see sequence
  Sequence
  In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
  
  
• Infinite sequence - see sequence
  Sequence
  In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
  
  
• Divergent sequence - see limit of a sequence
  Limit of a sequence
  The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
  
   or divergent series
  Divergent series
  In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
  
  
• Convergent sequence - see limit of a sequence
  Limit of a sequence
  The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
  
   or convergent series
  • Cauchy sequence
    Cauchy sequence
    In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
    
     - a sequence whose elements become arbitrarily close to each other as the sequence progresses
• Convergent series - a series whose sequence of partial sums converges
• Divergent series
  Divergent series
  In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
  
   - a series whose sequence of partial sums diverges
• Power series - a series of the form
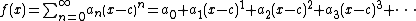
  • Taylor series
    Taylor series
    In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
    
     - a series of the form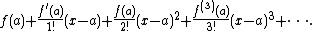
    • Maclaurin series - see Taylor series
      Taylor series
      In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
      
      
      • Binomial series
        Binomial series
        In mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f =  α, where is an arbitrary complex number...
        
         - the Maclaurin series of the function f given by f(x) = (1 + x) ^α
• Telescoping series
• Alternating series
• Geometric series
  • Divergent geometric series
• Harmonic series
  Harmonic series
  Harmonic series may refer to either of two related concepts:*Harmonic series *Harmonic series...
  
  
• Fourier series
  Fourier series
  In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
  
  
• Lambert series

Summation

Summation

Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...

 Methods

• Cesàro summation
  Cesàro summation
  In mathematical analysis, Cesàro summation is an alternative means of assigning a sum to an infinite series. If the series converges in the usual sense to a sum A, then the series is also Cesàro summable and has Cesàro sum A...
  
  
• Euler summation
  Euler summation
  Euler summation is a summability method for convergent and divergent series. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series....
  
  
• Lambert summation
  Lambert summation
  In mathematical analysis, Lambert summation is a summability method for a class of divergent series.-Definition:A series \sum a_n is Lambert summable to A, written \sum a_n = A , if...
  
  
• Borel summation
• Summation by parts - transforms the summation of products of into other summations
• Cesàro mean
• Abel's summation formula

More advanced topics

• Convolution
  Convolution
  In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
  
  
  • Cauchy product - is the discrete convolution of two sequences
• Farey sequence
  Farey sequence
  In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....
  
   - the sequence of completely reduced fractions between 0 and 1
• Oscillation
  Oscillation (mathematics)
  In mathematics, oscillation is the behaviour of a sequence of real numbers or a real-valued function, which does not converge, but also does not diverge to +∞ or −∞; that is, oscillation is the failure to have a limit, and is also a quantitative measure for that.Oscillation is defined as the...
  
   - is the behaviour of a sequence of real numbers or a real-valued function, which does not converge, but also does not diverge to +∞ or −∞; and is also a quantitative measure for that.
• Indeterminate form
  Indeterminate form
  In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...
  
  s - algerbraic expressions gained in the context of limits. The indeterminate forms include 0⁰, 0/0, 1^∞, ∞ − ∞, ∞/∞, 0 × ∞, and ∞⁰.

Convergence

• Pointwise convergence
  Pointwise convergence
  In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
  
  , Uniform convergence
• Absolute convergence
  Absolute convergence
  In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
  
  , Conditional convergence
• Normal convergence
  Normal convergence
  In mathematics normal convergence is a type of convergence for series of functions. Like absolute-convergence, it has the useful property that it is preserved when the order of summation is changed.- History :...
  
  

• Radius of convergence
  Radius of convergence
  In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
  
  

Convergence tests

Convergence tests

In mathematics, convergence tests are methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence or divergence of an infinite series.- List of tests :...

• Integral test for convergence
  Integral test for convergence
  In mathematics, the integral test for convergence is a method used to test infinite series of non-negative terms for convergence. An early form of the test of convergence was developed in India by Madhava in the 14th century, and by his followers at the Kerala School...
  
  
• Cauchy's convergence test
• Ratio test
• Comparison test
  Comparison test
  In mathematics, the comparison test, sometimes called the direct comparison test or CQT is a criterion for convergence or divergence of a series whose terms are real or complex numbers...
  
  
• Root test
• Alternating series test
  Alternating series test
  The alternating series test is a method used to prove that infinite series of terms converge. It was discovered by Gottfried Leibniz and is sometimes known as Leibniz's test or the Leibniz criterion.A series of the form...
  
  
• Cauchy condensation test
• Abel's test
  Abel's test
  In mathematics, Abel's test is a method of testing for the convergence of an infinite series. The test is named after mathematician Niels Abel...
  
  
• Dirichlet's test
  Dirichlet's test
  In mathematics, Dirichlet's test is a method of testing for the convergence of a series. It is named after mathematician Johann Dirichlet who published it in the Journal de Mathématiques Pures et Appliquées in 1862.- Statement :...
  
  
• Stolz–Cesàro theorem - is a criterion for proving the convergence of a sequence

Functions

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

• Function of a real variable
  Function of a real variable
  In mathematics, a function of a real variable is a mathematical function whose domain is the real line. More loosely, a function of a real variable is sometimes taken to mean any function whose domain is a subset of the real line....
  
  
• Continuous function
  Continuous function
  In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
  
  
  • Nowhere continuous function
  • Weierstrass function
    Weierstrass function
    In mathematics, the Weierstrass function is a pathological example of a real-valued function on the real line. The function has the property that it is continuous everywhere but differentiable nowhere...
    
    
• Smooth function
  Smooth function
  In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
  
  
  • Analytic function
    Analytic function
    In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
    
    
    • Quasi-analytic function
  • Non-analytic smooth function
    Non-analytic smooth function
    In mathematics, smooth functions and analytic functions are two very important types of functions. One can easily prove that any analytic function of a real argument is smooth...
    
    
  • Flat function
    Flat function
    In mathematics, especially real analysis, a flat function is a smooth function ƒ : ℝ → ℝ all of whose derivatives vanish at a given point x0 ∈ ℝ. The flat functions are, in some sense, the antitheses of the analytic functions...
    
    
  • Bump function
• Differentiable function
  Differentiable function
  In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
  
  
• Integrable function
  • Square-integrable function
    Square-integrable function
    In mathematics, a quadratically integrable function, also called a square-integrable function, is a real- or complex-valued measurable function for which the integral of the square of the absolute value is finite...
    
    , p-integrable function
• Monotonic function
  Monotonic function
  In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
  
  
  • Bernstein's theorem on monotone functions - states that any real-valued function on the half-line [0, ∞) that is totally monotone is a mixture of exponential functions
• Inverse function
  Inverse function
  In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
  
  
• Convex function
  Convex function
  In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
  
  , Concave function
  Concave function
  In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
  
  
• Singular function
• Harmonic function
  Harmonic function
  In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
  
  
  • Weakly harmonic function
  • Proper convex function
    Proper convex function
    In mathematical analysis and optimization, a proper convex function is a convex function f taking values in the extended real number line such thatf -\infty...
    
    
• Rational function
  Rational function
  In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
  
  
• Orthogonal function
• Implicit and explicit functions
  • Implicit function theorem
    Implicit function theorem
    In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
    
     - allows relations to be converted to functions
• Measurable function
  Measurable function
  In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
  
  
• Baire one star function
• Symmetric function
  Symmetric function
  In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
  
  

• Domain
• Codomain
  Codomain
  In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
  
  
  • Image
    Image (mathematics)
    In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
    
    
• Support
  Support (mathematics)
  In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
  
  

• Differential of a function
  Differential of a function
  In calculus, the differential represents the principal part of the change in a function y = ƒ with respect to changes in the independent variable. The differential dy is defined bydy = f'\,dx,...
  
  

Continuity

• Uniform continuity
  Uniform continuity
  In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
  
  
  • Modulus of continuity
    Modulus of continuity
    In mathematical analysis, a modulus of continuity is a function\omega:[0,\infty]\to[0,\infty]used to measure quantitatively the uniform continuity of functions. So, a function f:I\to\R admits \omega as a modulus of continuity if and only if|f-f|\leq\omega,for all x and y in the domain of f...
    
    
  • Lipschitz continuity
    Lipschitz continuity
    In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
    
    
• Semi-continuity
  Semi-continuity
  In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
  
  
• Equicontinuous
• Absolute continuity
  Absolute continuity
  In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
  
  
• Hölder condition
  Hölder condition
  In mathematics, a real or complex-valued function ƒ on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, \alpha , such that...
  
   - condition for Hölder continuity

Distribution

Distribution (mathematics)

In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...

s

• Dirac delta function
  Dirac delta function
  The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
  
  
• Heaviside step function
  Heaviside step function
  The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
  
  
• Hilbert transform
  Hilbert transform
  In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
  
  
• Green's function
  Green's function
  In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
  
  

Derivative

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

s

• Second derivative
  Second derivative
  In calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
  
  
  • Inflection point
    Inflection point
    In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
    
     - found using second derivatives
• Directional derivative
  Directional derivative
  In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
  
  , Total derivative
  Total derivative
  In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
  
  , Partial derivative
  Partial derivative
  In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
  
  

Differentiation rules

Differentiation rules

This article is a summary of the differentiation rules in elementary calculus, i.e. rules for computing the derivative of a function in calculus and mathematical analysis.-Nomenclature:...

• Linearity of differentiation
  Linearity of differentiation
  In mathematics, the linearity of differentiation is a most fundamental property of the derivative, in differential calculus. It follows from the sum rule in differentiation and the constant factor rule in differentiation...
  
  
• Product rule
  Product rule
  In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
  
  
• Quotient rule
• Chain rule
  Chain rule
  In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
  
  
• Inverse function theorem
  Inverse function theorem
  In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
  
   - gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain, also gives a formula for the derivative of the inverse function

Differentiation in Geometry and Topology

• Differentiable manifold
  Differentiable manifold
  A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
  
  
• Differentiable structure
• Submersion
  Submersion (mathematics)
  In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
  
   - a differentiable map between differentiable manifolds whose differential is everywhere surjective

Integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

s

• Antiderivative
  Antiderivative
  In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
  
  
  • Fundamental Theorem of Calculus
    Fundamental theorem of calculus
    The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
    
     - a theorem of anitderivatives
• Multiple integral
  Multiple integral
  The multiple integral is a type of definite integral extended to functions of more than one real variable, for example, ƒ or ƒ...
  
  
• Iterated integral
  Iterated integral
  In calculus an iterated integral is the result of applying integrals to a function of more than one variable in a way that each of the integrals considers some of the variables as given constants. For example, the function f, if y is considered a given parameter can be integrated with respect to...
  
  
• Improper integral
  Improper integral
  In calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....
  
  
  • Cauchy principal value
    Cauchy principal value
    In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
    
     - method for assigning values to certain improper integrals
• Line integral
  Line integral
  In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
  
  

• Anderson's theorem
  Anderson's theorem
  In mathematics, Anderson's theorem is a result in real analysis and geometry which says that the integral of an integrable, symmetric, unimodal, non-negative function f over an n-dimensional convex body K does not decrease if K is translated inwards towards the origin...
  
   - says that the integral of an integrable, symmetric, unimodal, non-negative function over an n-dimensional convex body (K) does not decrease if K is translated inwards towards the origin

Integration and Measure theory

• Riemann integral
  Riemann integral
  In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
  
   , Riemann sum
  Riemann sum
  In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
  
  
  • Riemann–Stieltjes integral
• Darboux integral
  Darboux integral
  In real analysis, a branch of mathematics, the Darboux integral or Darboux sum is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of...
  
  
• Lebesgue integration
  Lebesgue integration
  In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
  
  

Fundamental theorems

• Monotone convergence theorem - relates monotonicity with convergence
• Intermediate value theorem
  Intermediate value theorem
  In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
  
  - states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value
• Rolle's theorem
  Rolle's theorem
  In calculus, Rolle's theorem essentially states that a differentiable function which attains equal values at two distinct points must have a point somewhere between them where the first derivative is zero.-Standard version of the theorem:If a real-valued function ƒ is continuous on a closed...
  
  - essentially states that a differentiable function which attains equal values at two distinct points must have a point somewhere between them where the first derivative is zero
• Mean value theorem
  Mean value theorem
  In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
  
  - that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc
• Taylor's theorem
  Taylor's theorem
  In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
  
  - gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial.
• L'Hopital's rule
  L'Hôpital's rule
  In calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
  
  - uses derivatives to help evaluate limits involving indeterminate forms
• Abel's theorem
  Abel's theorem
  In mathematics, Abel's theorem for power series relates a limit of a power series to the sum of its coefficients. It is named after Norwegian mathematician Niels Henrik Abel.-Theorem:...
  
  - relates the limit of a power series to the sum of its coefficients
• Lagrange inversion theorem
  Lagrange inversion theorem
  In mathematical analysis, the Lagrange inversion theorem, also known as the Lagrange-Bürmann formula, gives the Taylor series expansion of the inverse function of an analytic function.-Theorem statement:...
  
  - gives the taylor series of the inverse of an analytic function
• Darboux's theorem
  Darboux's theorem (analysis)
  Darboux's theorem is a theorem in real analysis, named after Jean Gaston Darboux. It states that all functions that result from the differentiation of other functions have the intermediate value property: the image of an interval is also an interval....
  
  - states that all functions that result from the differentiation of other functions have the intermediate value property: the image of an interval is also an interval
• Heine-Borel theorem - sometimes used as the defining property of compactness
• Bolzano-Weierstrass theorem - states that each bounded sequence in Rⁿ has a convergent subsequence.

Real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s

• Construction of the real numbers
  • Natural number
    Natural number
    In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
    
    
  • Integer
    Integer
    The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
    
    
  • Rational number
    Rational number
    In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
    
    
  • Irrational number
    Irrational number
    In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
    
    
• Completeness of the real numbers
  Completeness of the real numbers
  Intuitively, completeness implies that there are not any “gaps” or “missing points” in the real number line. This contrasts with the rational numbers, whose corresponding number line has a “gap” at each irrational value...
  
  
• Least-upper-bound property
  Least-upper-bound property
  In mathematics, the least-upper-bound property is a fundamental property of the real numbers and certain other ordered sets. The property states that any non-empty set of real numbers that has an upper bound necessarily has a least upper bound ....
  
  
• Real line
  Real line
  In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
  
  
  • Extended real number line
    Extended real number line
    In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
    
    
  • Dedekind cut
    Dedekind cut
    In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
    
    

Sets

• Open set
  Open set
  The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
  
  
• Neighbourhood
  Neighbourhood (mathematics)
  In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
  
  
• Cantor set
  Cantor set
  In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
  
  
• Derived set (mathematics)
  Derived set (mathematics)
  In mathematics, more specifically in point-set topology, the derived set of a subset S of a topological space is the set of all limit points of S...
  
  

• Completeness
  Completeness (order theory)
  In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set . A special use of the term refers to complete partial orders or complete lattices...
  
  
• Limit superior and limit inferior
  Limit superior and limit inferior
  In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
  
  
  • Supremum
    Supremum
    In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
    
    
  • Infimum
    Infimum
    In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
    
    

• Interval
  Interval (mathematics)
  In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
  
  
  • Partition of an interval
    Partition of an interval
    In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
    
    

Maps

Map (mathematics)

In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...

• Contraction mapping
  Contraction mapping
  In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
  
  
• Metric map
• Fixed point
  Fixed point (mathematics)
  In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
  
   - a point of a function that maps to itself

Infinite expressions

Infinite expression (mathematics)

In mathematics, an infinite expression is an expression in which some operators take an infinite number of arguments, or in which the nesting of the operators continues to an infinite depth...

• Continued fraction
  Continued fraction
  In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
  
  
• Series
  Series (mathematics)
  A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
  
  
• Infinite products

Inequalities

• Triangle inequality
  Triangle inequality
  In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
  
  
• Bernoulli's inequality
  Bernoulli's inequality
  In real analysis, Bernoulli's inequality is an inequality that approximates exponentiations of 1 + x.The inequality states that^r \geq 1 + rx\!...
  
  
• Cauchy-Schwarz inequality
• Triangle inequality
  Triangle inequality
  In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
  
  
• Hölder's inequality
  Hölder's inequality
  In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
  
  
• Minkowski inequality
  Minkowski inequality
  In mathematical analysis, the Minkowski inequality establishes that the Lp spaces are normed vector spaces. Let S be a measure space, let 1 ≤ p ≤ ∞ and let f and g be elements of Lp...
  
  
• Jensen's inequality
  Jensen's inequality
  In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...
  
  
• Chebyshev's inequality
  Chebyshev's inequality
  In probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
  
  
• Inequality of arithmetic and geometric means
  Inequality of arithmetic and geometric means
  In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...
  
  

Mean

Mean

In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....

s

• Generalized mean
  Generalized mean
  In mathematics, a generalized mean, also known as power mean or Hölder mean , is an abstraction of the Pythagorean means including arithmetic, geometric, and harmonic means.-Definition:...
  
  
• Pythagorean means
  Pythagorean means
  In mathematics, the three classical Pythagorean means are the arithmetic mean , the geometric mean , and the harmonic mean...
  
  
  • Arithmetic mean
    Arithmetic mean
    In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
    
    
  • Geometric mean
    Geometric mean
    The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
    
    
  • Harmonic mean
    Harmonic mean
    In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
    
    
• Geometric-harmonic mean
  Geometric-harmonic mean
  In mathematics, the geometric-harmonic mean M of two positive real numbers x and y is defined as follows: we form the geometric mean of g0 = x and h0 = y and call it g1, i.e. g1 is the square root of xy. We also form the harmonic mean of x and y and call it h1, i.e...
  
  
• Arithmetic-geometric mean
• Weighted mean
  Weighted mean
  The weighted mean is similar to an arithmetic mean , where instead of each of the data points contributing equally to the final average, some data points contribute more than others...
  
  
• Quasi-arithmetic mean
  Quasi-arithmetic mean
  In mathematics and statistics, the quasi-arithmetic mean or generalised f-mean is one generalisation of the more familiar means such as the arithmetic mean and the geometric mean, using a function f...
  
  

Orthogonal polynomials

Orthogonal polynomials

In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...

• Classical orthogonal polynomials
  • Hermite polynomials
    Hermite polynomials
    In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
    
    
  • Laguerre polynomials
    Laguerre polynomials
    In mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
    
    
  • Jacobi polynomials
    Jacobi polynomials
    In mathematics, Jacobi polynomials are a class of classical orthogonal polynomials. They are orthogonal with respect to the weight ^\alpha ^\beta on the interval [-1, 1]...
    
    
  • Gegenbauer polynomials
    Gegenbauer polynomials
    In mathematics, Gegenbauer polynomials or ultraspherical polynomials C are orthogonal polynomials on the interval [−1,1] with respect to the weight function α–1/2. They generalize Legendre polynomials and Chebyshev polynomials, and are special cases of Jacobi polynomials...
    
    
  • Legendre polynomials

Spaces

• Euclidean space
  Euclidean space
  In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
  
  
• Metric space
  Metric space
  In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
  
  
  • Banach fixed point theorem
    Banach fixed point theorem
    In mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
    
     - guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, provides method to find them
  • Complete metric space
• Topological space
  Topological space
  Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
  
  
  • Function space
    Function space
    In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
    
    
    • Sequence space
      Sequence space
      In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
      
      
• Compact space
  Compact space
  In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
  
  

Measures

Measure (mathematics)

In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...

• Lebesgue measure
  Lebesgue measure
  In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
  
  
• Outer measure
  Outer measure
  In mathematics, in particular in measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. A general theory of outer measures was first introduced by...
  
  
  • Hausdorff measure
    Hausdorff measure
    In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
    
    

• Dominated convergence theorem
  Dominated convergence theorem
  In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
  
   - provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions.

Historical figures

• Michel Rolle
  Michel Rolle
  Michel Rolle was a French mathematician. He is best known for Rolle's theorem , and he deserves to be known as the co-inventor in Europe of Gaussian elimination .-Life:...
  
   (1652-1719)
• Brook Taylor
  Brook Taylor
  Brook Taylor FRS was an English mathematician who is best known for Taylor's theorem and the Taylor series.- Life and work :...
  
   (1685-1731)
• Leonhard Euler
  Leonhard Euler
  Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
  
   (1707-1783)
• Joseph Louis Lagrange
  Joseph Louis Lagrange
  Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
  
   (1736-1813)
• Jean Baptiste Joseph Fourier (1768-1830)
• Bernard Bolzano
  Bernard Bolzano
  Bernhard Placidus Johann Nepomuk Bolzano , Bernard Bolzano in English, was a Bohemian mathematician, logician, philosopher, theologian, Catholic priest and antimilitarist of German mother tongue.-Family:Bolzano was the son of two pious Catholics...
  
   (1781-1848)
• Augustin Cauchy (1789-1857)
• Niels Henrik Abel
  Niels Henrik Abel
  Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
  
   (1802-1829)
• Johann Peter Gustav Lejeune Dirichlet
  Johann Peter Gustav Lejeune Dirichlet
  Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
  
   (1805-1859)
• Karl Weierstrass
  Karl Weierstrass
  Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
  
   (1815-1897)
• Eduard Heine
  Eduard Heine
  Heinrich Eduard Heine was a German mathematician.Heine became known for results on special functions and in real analysis. In particular, he authored an important treatise on spherical harmonics and Legendre functions . He also investigated basic hypergeometric series...
  
   (1821-1881)
• Pafnuty Chebyshev
  Pafnuty Chebyshev
  Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
  
   (1821-1894)
• Leopold Kronecker
  Leopold Kronecker
  Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
  
   (1823-1891)
• Bernhard Riemann
  Bernhard Riemann
  Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
  
   (1826-1866)
• Richard Dedekind
  Richard Dedekind
  Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
  
   (1831-1916)
• Rudolf Lipschitz
  Rudolf Lipschitz
  Rudolf Otto Sigismund Lipschitz was a German mathematician and professor at the University of Bonn from 1864. Peter Gustav Dirichlet was his teacher. He supervised the early work of Felix Klein....
  
   (1832-1903)
• Camille Jordan
  Camille Jordan
  Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
  
   (1838-1922)
• Jean Gaston Darboux
  Jean Gaston Darboux
  Jean-Gaston Darboux was a French mathematician.-Life:Darboux made several important contributions to geometry and mathematical analysis . He was a biographer of Henri Poincaré and he edited the Selected Works of Joseph Fourier.Darboux received his Ph.D...
  
   (1842-1917)
• Georg Cantor
  Georg Cantor
  Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
  
   (1845-1918)
• Ernesto Cesàro
  Ernesto Cesàro
  Ernesto Cesàro was an Italian mathematician who worked in the field of differential geometry.Cesàro was born in Naples. He is known also for his 'averaging' method for the summation of divergent series, known as the Cesàro mean.-Books by E. Cesaro:* * Ernesto Cesàro (March 12, 1859 – September...
  
   (1859-1906)
• Otto Hölder
  Otto Hölder
  Otto Ludwig Hölder was a German mathematician born in Stuttgart.Hölder first studied at the Polytechnikum and then in 1877 went to Berlin where he was a student of Leopold Kronecker, Karl Weierstraß, and Ernst Kummer.He is famous for many things including: Hölder's inequality, the Jordan–Hölder...
  
   (1859-1937)
• Hermann Minkowski
  Hermann Minkowski
  Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
  
   (1864-1909)
• Alfred Tauber
  Alfred Tauber
  Alfred Tauber was a mathematician who was born in Bratislava, and died in the Theresienstadt concentration camp. In 1897 he proved a corrected converse of Abel's theorem. G.H. Hardy and J.E. Littlewood coined the term Tauberian to describe converse theorems like that proved by Tauber.- External...
  
   (1866-1942)
• Felix Hausdorff
  Felix Hausdorff
  Felix Hausdorff was a Jewish German mathematician who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, function theory, and functional analysis.-Life:Hausdorff studied at the University of Leipzig,...
  
   (1868-1942)
• Émile Borel
  Émile Borel
  Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
  
   (1871-1956)
• Henri Lebesgue
  Henri Lebesgue
  Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
  
   (1875-1941)
• Waclaw Sierpinski (1882-1969)
• Johann Radon
  Johann Radon
  Johann Karl August Radon was an Austrian mathematician. His doctoral dissertation was on calculus of variations .- Life :...
  
   (1887-1956)
• Karl Menger
  Karl Menger
  Karl Menger was a mathematician. He was the son of the famous economist Carl Menger. He is credited with Menger's theorem. He worked on mathematics of algebras, algebra of geometries, curve and dimension theory, etc...
  
   (1902-1985)

Related fields of analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

• Asymptotic analysis
  Asymptotic analysis
  In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
  
  - studies a method of describing limiting behaviour
• Convex analysis
  Convex analysis
  Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
  
  - studies the properties of convex functions and convex sets
  • List of convexity topics
• Harmonic analysis
  Harmonic analysis
  Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
  
  - studies the representation of functions or signals as superpositions of basic waves
  • List of harmonic analysis topics
• Fourier analysis - studies Fourier series and Fourier transforms
  • List of fourier analysis topics
  • List of Fourier-related transforms
• Complex analysis
  Complex analysis
  Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
  
  - studies the extension of real analysis to include complex numbers
• Functional analysis
  Functional analysis
  Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
  
  - studies vector spaces endowed with limit-related structures and the linear operators acting upon these spaces