List of algebraic structures
Encyclopedia
In universal algebra
, a branch of pure mathematics
, an algebraic structure
is a variety
or quasivariety
. Abstract algebra
is primarily the study of algebraic structures and their properties. Some axiom
atic formal system
s that are neither varieties nor quasivarieties, called nonvarieties below, are included among the algebraic structures by tradition.
Other web lists of algebraic structures, organized more or less alphabetically, include Jipsen and PlanetMath. These lists mention many structures not included below, and may present more information about some structures than is presented here.
, functions
, and relations
, satisfying a number of axiom
s, including none. This definition of an algebraic structure should not be taken as restrictive. Anything that satisfies the axioms defining a structure is an instance of that structure, regardless of how many other axioms that instance happens to satisfy. For example, all groups
are also semigroup
s and magmas
.
Structures are listed below in approximate order of increasing complexity as follows:
If structure B is under structure A and more indented, then A is interpretable
in B, meaning that all theorem
s of A are theorems of B. The converse
is usually not the case.
A structure is trivial
if the cardinality of S is less than 2, and is otherwise nontrivial.
are equations formulated using only the operations the structure allows, and variables that are tacitly universally quantified over a set that is part of the definition of the structure. Hence identities contain no sentential connective
s, existentially quantified variables
, or relations
of any kind other than equality and the operations the structure allows.
If the axioms defining an algebraic structure are all identities--or can be recast as identities
--the structure is a variety
(not to be confused with algebraic variety
in the sense of algebraic geometry
). Nonidentities can often be recast as identities. For example, any lattice inequality
of the form α≤β can always be recast as the identity α∧β=α.
An important result is that given any variety C and any underlying set X, the free object
F(X)∈C exists.
.
for a list of the many properties that a group-like structures may possess. The diagram to the right summarizes the defining properties of:
All group-like structures feature a primary (and often unique) binary
or ternary operation
, which usually (e.g., for semigroup
s and hoops) associates
. This operation will nearly always be denoted here by concatenation, and when it is binary, will be called "group product." If group product associates, brackets are not required to resolve the order of operation. When group product does not associate (e.g., quasigroup
s, semiheaps
, loops
, implication algebras), an embedded period indicates the grouping. Examples: xy.z, x.yz.
For Steiner magmas
, abelian group
s, logic algebras, bands, equivalence algebras, and hoops, group product also commutes. Commutativity
may be added to any group-like structure for which it is not already the case.
Groups
, logic algebras, lattices
, and loops feature a unary operation
, denoted here by enclosure in parentheses.
For monoid
s, loops, and sloops, S is a pointed set
.
One binary operation
.
Two binary operation
s.
Three binary operation
s.
In addition to group product, quasigroups feature 2 binary operations denoted by infix
"/" and "\". These added operations permit axiomatizing the defining property of quasigroups, cancellation
, by means of identities alone.
The following diagram summarizes two possible paths from magma to group.
NOTE:
One ternary operation
, heap product, denoted xyz:
and join, which characterize nearly all structures in this section, are idempotent, by assumption or proof. Latticoids are the only lattice-like structure that do not associate. N.B. "Lattice" is also employed in a number of group-theoretic contexts
, including to refer to a discrete subgroup of the real vector space Rn that spans Rn.
Some concepts from order theory
that recur in lattice theory:
One binary operation
, one of meet
or join, and denoted by concatenation
. The two structures below are also magmas
; see the preceding section.
Two binary operations, meet
(infix
∧) and join (infix ∨). Duality
means that interchanging all meets and joins preserves truth.
Three binary operations:
Four or more binary operations:
The following Hasse diagram
illustrates some pathways from a very general concept, partially ordered set
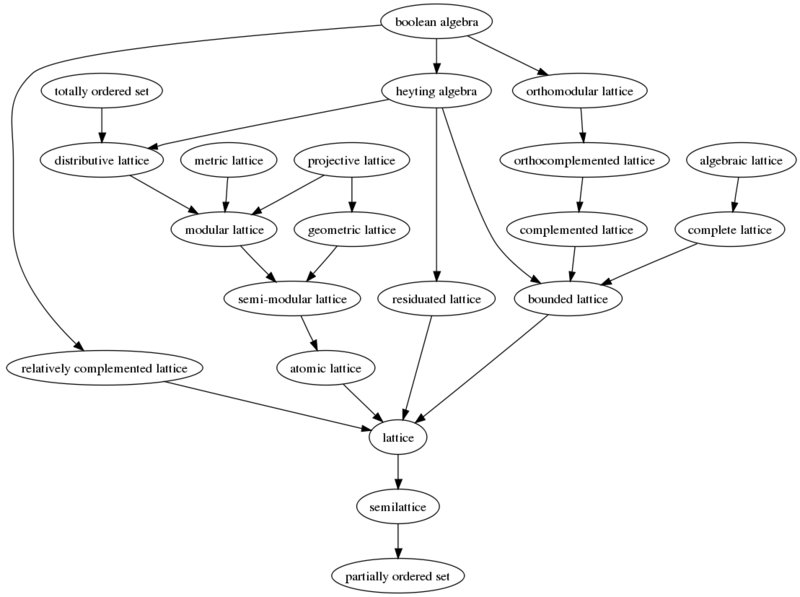
s, to the oldest and most researched lattice, Boolean algebra. This diagram reveals some of the hierarchical structure linking a number of important types of lattices, not all discussed above because some are not varieties. This diagram consists of a number of links of the form A→B, each meaning that structure A is included in structure B.
, monoid
, group
, or a ring
are satisfied.
N.B. The above definitions of rng, ring, and semiring do not command universal assent:
, denoted by Greek letters, and a set S whose members are denoted by Latin letters. For every ring R, there is a corresponding variety
of R-modules.
R is a ring
and S is a monoid
.Module
: S is an abelian group with operators
, each unary operator indexed by R. The operators are scalar multiplication
RxS→S, which commutes, associates, is unital, and distributes over module and scalar addition. If only the pre(post)multiplication of module elements by scalars is defined, the result is a left (right) module.
. Algebra over a ring (also R-algebra): a module where R is a commutative ring
. There is a second binary operation over S, called multiplication and denoted by concatenation, which distributes over module addition and is bilinear: α(xy) = (αx)y = x(αy).
of functions.Jordan algebra
: an algebra over a field whose vector multiplication commutes, may or may not associate, and satisfies the Jordan identity.
Lie algebra
: an algebra over a field satisfying the Jacobi identity
. The vector multiplication, the Lie bracket
denoted [u,v], anticommutes, usually does not associate, and is nilpotent
.
is a variety with one or more axioms that are quasiidentities
. Let Greek letters be metavariables denoting identities
. A quasiidentity then takes the form (α1∧,...,∧αn) → β.
(sometimes called "groupoid", or "algebra of type (2)") is a set equipped with a binary operation.
Monoid
: a unital cancellative semigroup.
.Combinatory logic
: A combinator concatenates upper case letters. Terms
concatenate combinators and lower case letters. Concatenation is left and right cancellative
. '=' is an equivalence relation
over terms. The axioms are Sxyz = xz.yz and Kxy = x; these implicitly define the primitive combinators S and K. The distinguished elements I and 1, defined as I=SK.K and 1=S.KI, have the provable properties Ix=x and 1xy=xy. Combinatory logic has the expressive power of set theory
.
, and a binary relation
E⊆V2, adjacency, consisting of edges. No operations.Graph
: A directed graph such that E is symmetric. Dropping the requirement that E be irreflexive makes loops
possible.
Linearly ordered group
and ordered ring
: S is linearly ordered;
Ordered field
: a field
whose S is totally ordered by '≤,' so that (a≤b)→(a+c≤b+c) and (0≤a,b)→ (0≤ab).
atized solely with identities
and quasiidentities
. Many nonidentities are of three very simple kinds:
, namely one such that S≠{0}, 0 being the additive identity element
. The nearest thing to an identity implying S≠{0} is the nonidentity 0≠1, which requires that the additive and multiplicative identities be distinct.Axioms involving multiplication, holding for all members of S (or R or K) except 0. In order for an algebraic structure to be a variety, the domain
of each operation must be an entire underlying set; there can be no partial operations."0 is not the successor of anything," included in nearly all arithmetics.
Most of the classic results of universal algebra
do not hold for nonvarieties. For example, neither the free field
over any set nor the direct product
of integral domains exists. Nevertheless, nonvarieties often retain an undoubted algebraic flavor.
There are whole classes of axiom
atic formal system
s not included in this section, e.g., logic
s, topological space
s, and this exclusion is in some sense arbitrary. Many of the nonvarieties below were included because of their intrinsic interest and importance, either by virtue of their foundational nature (Peano arithmetic), ubiquity (the real field
), or richness (e.g., fields
, normed vector spaces). Also, a great deal of theoretical physics can be recast using the nonvarieties called multilinear algebra
s.
No operations. Functions or relations may be present:
s. There is a multifunction
m: S→N such that m(x) is the multiplicity
of x∈S.
s addition
and multiplication
. If both operations are included, the recursive identity defining multiplication usually links them. Arithmetics necessarily have infinite models
.
In the structures below, addition and multiplication, if present, are recursively
defined by means of an injective operation called successor, denoted by prefix σ. 0 is the axiomatic identity element
for addition, and annihilates multiplication. Both axioms hold for semiring
s.
Arithmetics above this line are decidable
. Those below are incompletable.
The following arithmetics lack a connection between addition and multiplication. They are the simplest arithmetics capable of expressing all primitive recursive function
s.
Two sets, Φ and D.
under combination, an idempotent operation. The operation of focussing, f: ΦxD→Φ satisfies the axiom f(f(φ,x),y)=f(φ,x∧y) and distributes over combination. Every element of Φ has an identity element in D under focussing.
s, addition and multiplication. S is nontrivial, i.e., S≠{0}. S-0 is S with 0 removed.
s. Principal ideal domain
: an integral domain in which every ideal is principal
, i.e., can be generated by a single element.
Euclidean domain
: an integral domain with a function f: S→N satisfying the division with remainder property
.
under multiplication.
over addition. x0 = 0 is a theorem.
s.Ordered field
: a field whose S is totally ordered by '≤', so that (a≤b)→(a+c≤b+c) and (0≤a,b)→ (0≤ab).
Real field
: a Dedekind complete ordered field. x+y) = ∂x+ ∂y, and satisfying the product rule
, ∂(xy) = ∂xy + x∂y.
The following field-like structures are not varieties for reasons in addition to S≠{0}: Artinian ring
: a ring whose ideals
satisfy the descending chain condition.
s that are not varieties. Two sets: M is a set of vectors and R is a set of scalar
s.
Three binary operations.
, and positive definite
.
, whose norm is the square root of the inner product, M×M→R. Let i,j, and n be positive integers such that 1≤i,j≤n. Then M has an orthonormal basis
such that ei•ej = 1 if i=j and 0 otherwise. See free module
.Unitary space
: Differs from inner product spaces in that R is the complex field, and the inner product has a different name, the hermitian inner product, with different properties: conjugate
symmetric, bilinear, and positive definite
.Graded vector space
: a vector space such that the members of M have a direct sum decomposition. See graded algebra
below.
Structures that build on the notion of vector space:
s. Two sets, V and K:
s (including vectors
), denoted by lower case Latin letters. V is an abelian group
under multivector
addition, and a monoid
under outer product
. The outer product goes under various names, and is multilinear
in principle but usually bilinear. The outer product defines the multivectors recursively starting from the vectors. Thus the members of V have a "degree" (see graded algebra
below). Multivectors may have an inner product as well, denoted u•v: V×V→K, that is symmetric, linear
, and positive definite
; see inner product space
above. The properties and notation of K are the same as those of R above, except that K may have -1 as a distinguished member. K is usually the real field
, as multilinear algebras are designed to describe physical phenomena without complex number
s. The scalar multiplication
of scalars and multivectors, V×K→V, has the same properties as module
scalar multiplication.
A, such that the Lie algebra AL contains L. Graded algebra
: an associative algebra with unital outer product. The members of V have a directram decomposition resulting in their having a "degree," with vectors having degree 1. If u and v have degree i and j, respectively, the outer product of u and v is of degree i+j. V also has a distinguished member 0 for each possible degree. Hence all members of V having the same degree form an Abelian group
under addition.
. All multilinear algebras can be seen as special cases of tensor algebra.
. v1 ∧ v2 ∧ ... ∧ vk = 0 if and only if v1, ..., vk are linearly dependent. Multivectors also have an inner product. Geometric algebra
: an exterior algebra whose exterior (called geometric) product is denoted by concatenation. The geometric product of parallel multivectors commutes, that of orthogonal vectors anticommutes. The product of a scalar with a multivector commutes. vv yields a scalar.
or is a manifold
, characteristics that are not algebraic in nature. This added structure must be compatible in some sense, however, with the algebraic structure. The case of when the added structure is partial order is discussed above, under varieties.
Topology
:
Manifold
:
Let x and y be any two elements of M. Then there exist:
.A binary partial operation
over M, called composition
and denoted by concatenation
. xy is defined iff
c(x)=d(y). If xy is defined, d(xy) = d(x) and c(xy) = c(y).
Category
: Composition
associates (if defined), and x has left
and right identity
elements, the domain and codomain of x, respectively, so that d(x)x = x = xc(x). Letting φ stand for one of c or d, and γ stand for the other, then φ(γ(x)) = γ(x).
If O has but one element, the associated category is a monoid
.
. Equivalently, a category such that every element x of M, x(a,b), has an inverse x(b,a); see diagram in section 2.2. Algebraic definition: A group whose product is a partial function
. Group product associates in that if ab and bc are both defined, then ab.c=a.bc. (a)a and a(a) are always defined. Also, ab.(b) = a, and (a).ab = b.
s; C=complex number
s.
A Dedekind algebra is a free S-algebra
on zero generators
of type 〈1,0〉. Freeness implies that no two terms are equal. Very general results from the theory of free algebras, e.g., definition by recursion, and uniqueness up to isomorphism, are now applicable.
A Dedekind-Peano structure
is a free object
with one generator
.
The universe
of singletons forms a Dedekind-Peano structure
if {x} interprets the successor of x, and the null set
interprets 0.
Also see examples of groups
, list of small groups, and list of finite simple groups.
Lie groups: See table of Lie groups
and list of simple Lie groups.
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, a branch of pure mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
is a variety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
or quasivariety
Quasivariety
In mathematics, a quasivariety is a class of algebraic structures generalizing the notion of variety by allowing equational conditions on the axioms defining the class.-Definition:...
. Abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
is primarily the study of algebraic structures and their properties. Some axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
atic formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
s that are neither varieties nor quasivarieties, called nonvarieties below, are included among the algebraic structures by tradition.
Other web lists of algebraic structures, organized more or less alphabetically, include Jipsen and PlanetMath. These lists mention many structures not included below, and may present more information about some structures than is presented here.
Generalities
An algebraic structure consists of one or two sets closed under some operationsOperation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
, functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, and relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
, satisfying a number of axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s, including none. This definition of an algebraic structure should not be taken as restrictive. Anything that satisfies the axioms defining a structure is an instance of that structure, regardless of how many other axioms that instance happens to satisfy. For example, all groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
are also semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s and magmas
Magma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
.
Structures are listed below in approximate order of increasing complexity as follows:
- Structures that are varietiesVariety (universal algebra)In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
precede those that are not; - Simple structures built on one underlying set S precede composite structures built on two;
- If A and B are the two underlying sets making up a composite structure, that structure may include functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the form AxA→B or AxB→A. - Structures are then ordered by the number and aritiesArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
of the operations they contain. The heapHeap (mathematics)In abstract algebra, a heap is a mathematical generalisation of a group. Informally speaking, a heap is obtained from a group by "forgetting" which element is the unit, in the same way that an affine space can be viewed as a vector space in which the 0 element has been "forgotten"...
, a group-like structure, is the only structure mentioned in this entry requiring an operation whose arityArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
exceeds 2.
If structure B is under structure A and more indented, then A is interpretable
Interpretability
In mathematical logic, interpretability is a relation between formal theories that expresses the possibility of interpreting or translating one into the other.-Informal definition:Assume T and S are formal theories...
in B, meaning that all theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s of A are theorems of B. The converse
Inverse relation
In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
is usually not the case.
A structure is trivial
Trivial (mathematics)
In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
if the cardinality of S is less than 2, and is otherwise nontrivial.
Varieties
IdentitiesIdentity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
are equations formulated using only the operations the structure allows, and variables that are tacitly universally quantified over a set that is part of the definition of the structure. Hence identities contain no sentential connective
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
s, existentially quantified variables
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
, or relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
of any kind other than equality and the operations the structure allows.
If the axioms defining an algebraic structure are all identities--or can be recast as identities
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
--the structure is a variety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
(not to be confused with algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
in the sense of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
). Nonidentities can often be recast as identities. For example, any lattice inequality
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
of the form α≤β can always be recast as the identity α∧β=α.
An important result is that given any variety C and any underlying set X, the free object
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
F(X)∈C exists.
Simple structures
No binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
.
- Set: a degenerate algebraic structure having no operations.
- Pointed setPointed setIn mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
: S has one or more distinguished elements. While pointed sets are near-trivial, they lead to discrete spaceDiscrete spaceIn topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
s, which are not.- Bipointed set: S has exactly two distinguished elements.
- Unary system: S and a single unary operationUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
over S. - Pointed unary system: a unary system with S a pointed set.
Group-like structures
See magmaMagma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
for a list of the many properties that a group-like structures may possess. The diagram to the right summarizes the defining properties of:
- The better-known group-like structures, from the least (magmas) to the most restrictive (groups);
- The related notions of categoryCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
and groupoidGroupoidIn mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
.
All group-like structures feature a primary (and often unique) binary
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
or ternary operation
Ternary operation
In mathematics, a ternary operation is an n-ary operation with n = 3. A ternary operation on a set A takes any given three elements of A and combines them to form a single element of A. An example of a ternary operation is the product in a heap....
, which usually (e.g., for semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s and hoops) associates
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
. This operation will nearly always be denoted here by concatenation, and when it is binary, will be called "group product." If group product associates, brackets are not required to resolve the order of operation. When group product does not associate (e.g., quasigroup
Quasigroup
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
s, semiheaps
Heap (mathematics)
In abstract algebra, a heap is a mathematical generalisation of a group. Informally speaking, a heap is obtained from a group by "forgetting" which element is the unit, in the same way that an affine space can be viewed as a vector space in which the 0 element has been "forgotten"...
, loops
Quasigroup
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
, implication algebras), an embedded period indicates the grouping. Examples: xy.z, x.yz.
For Steiner magmas
Steiner system
250px|right|thumbnail|The [[Fano plane]] is an S Steiner triple system. The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line....
, abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, logic algebras, bands, equivalence algebras, and hoops, group product also commutes. Commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
may be added to any group-like structure for which it is not already the case.
Groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, logic algebras, lattices
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, and loops feature a unary operation
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
, denoted here by enclosure in parentheses.
For monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s, loops, and sloops, S is a pointed set
Pointed set
In mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
.
One binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
.
- Magma or groupoidMagma (algebra)In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
: S is closed under a single binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
.- Steiner magmaSteiner system250px|right|thumbnail|The [[Fano plane]] is an S Steiner triple system. The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line....
: A commutative magma satisfying x.xy = y.- SquagSteiner system250px|right|thumbnail|The [[Fano plane]] is an S Steiner triple system. The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line....
: an idempotent Steiner magma. - SloopSteiner system250px|right|thumbnail|The [[Fano plane]] is an S Steiner triple system. The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line....
: a Steiner magma with distinguished element 1, such that xx = 1.
- Squag
- Equivalential algebra: a magma satisfying xx.y=y, xy.z.z=xy, and xy.xzz.xzz=xy.
- Implicational calculus: a magma satisfying xy.x=x, x.yz=y.xz, and xy.y=yx.x.
- Equivalence algebra: an idempotent magmaMagma (algebra)In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
satisfying xy.x=x, x.yz=xy.xz, and xy.z.y.x = xz.y.x. - SemigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
: an associative magma.- Semigroup with involutionSemigroup with involutionIn mathematics, in semigroup theory, an involution in a semigroup is a transformation of the semigroup which is its own inverse and which is an anti-automorphism of the semigroup. A semigroup in which an involution is defined is called a semigroup with involution...
: a semigroup with a unary operation, involution, denoted by enclosure in parentheses, such that ((x))=x and (xy) = (y)(x). - Equivalential calculus: a commutative semigroup satisfying yyx=x.
- MonoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
: a unital semigroup.- Boolean group: a monoid with xx = identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. - GroupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
: a monoid with a unary operationUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
, inverse, denoted by enclosure in parentheses, and satisfying (a)a = identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
.- Abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
: a commutative group. The single axiom yxz(yz)=x suffices. - Group with operatorsGroup with operatorsIn abstract algebra, a branch of pure mathematics, the algebraic structure group with operators or Ω-group is a group with a set of group endomorphisms.Groups with operators were extensively studied by Emmy Noether and her school in the 1920s...
: a group closed under one or more unary operations, with each such operation distributing over group product. - Algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
:- Reductive groupReductive groupIn mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
: an algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
such that the unipotent radical of the identity component of S is trivial.
- Reductive group
- Abelian group
- Logic algebra: a commutative monoid with a unary operationUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
, complementationComplemented latticeIn the mathematical discipline of order theory, a complemented lattice is a bounded lattice in which every element a has a complement, i.e. an element b satisfying a ∨ b = 1 and a ∧ b = 0....
, denoted by enclosure in parentheses, and satisfying x(1)=(1) and ((x))=x. 1 and (1) are lattice boundsLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
for S.- MV-algebraMV-algebraIn abstract algebra, a branch of pure mathematics, an MV-algebra is an algebraic structure with a binary operation \oplus, a unary operation \neg, and the constant 0, satisfying certain axioms...
: a logic algebra satisfying the axiom ((x)y)y = ((y)x)x. - Boundary algebraLaws of FormLaws of Form is a book by G. Spencer-Brown, published in 1969, that straddles the boundary between mathematics and philosophy...
: a logic algebra satisfying (x)x=1 and (xy)y = (x)y, from which it can be proved that boundary algebra is a distributive latticeDistributive latticeIn mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
. (0)=1, (1)=0, ((x))=x and xx=x are now provable.
- MV-algebra
- Boolean group: a monoid with xx = identity element
- Semigroup with involution
- Order (algebra): an idempotent magma satisfying yx=xy.x, xy=xy.y, x:xy.z=x.yz, and xy.z.y=xz.y. Hence idempotence holds in the following wide sense. For any subformula x of formula z: (i) all but one instance of x may be erased; (ii) x may be duplicated at will anywhere in z.
- BandSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
: an associative order algebra, and an idempotent semigroup.- Rectangular band: a band satisfying the axiom xyz = xz.
- Normal band: a band satisfying the axiom xyzx = xzyx.
- Band
- Steiner magma
-
- The following two structures form a bridge connecting magmasMagma (algebra)In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
and latticesLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
:- SemilatticeSemilatticeIn mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
: a commutative band. The binary operation is called meetMeet (mathematics)In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
or join.
-
- LatticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
: a semilattice with a unary operation, dualization, denoted (x) and satisfying the absorption lawAbsorption lawIn algebra, the absorption law or absorption identity is an identity linking a pair of binary operations.Two binary operations, say ¤ and *, are said to be connected by the absorption law if:...
, x(xy) = (x(xy)) = x. xx = x is now provable.
- Lattice
- Semilattice
- The following two structures form a bridge connecting magmas
Two binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s.
- Rack: Infix ◅ and ▻ denote the two operations. The axioms are x▻(y▻z) = (x▻y)▻(x▻z), (z◅y)◅x = (z◅x)◅(y◅x), (x▻y)◅x = y, and x▻(y◅x) = y. A simpler but nonequational way of stating an important fact about racks is that ∀x,y∈S, there exists a unique z such that x▻z = y. Asserting this makes redundant the operation denoted by ◅.
- Quandle: Either of the rack operations is idempotent.
- Hoop: a commutative monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
with a second binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
, denoted by infixInfixAn infix is an affix inserted inside a word stem . It contrasts with adfix, a rare term for an affix attached to the end of a stem, such as a prefix or suffix.-Indonesian:...
→, satisfying the axioms x→.y→z = xy.→z, x→x = 1, and x→y.x = y→x.y.
Three binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s.
In addition to group product, quasigroups feature 2 binary operations denoted by infix
Infix
An infix is an affix inserted inside a word stem . It contrasts with adfix, a rare term for an affix attached to the end of a stem, such as a prefix or suffix.-Indonesian:...
"/" and "\". These added operations permit axiomatizing the defining property of quasigroups, cancellation
Cancellation property
In mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
, by means of identities alone.
- QuasigroupQuasigroupIn mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
: a cancellativeCancellation propertyIn mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
magmaMagma (algebra)In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
. A quasigroup satisfies the axioms y = x(x\y) = x\(xy) = (y/x)x = (yx)/x. The following equivalent but nonvariety definition may be more intuitive. S is a quasigroup iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
∀x,y∈S, ∃a,b∈S, such that xa = y and bx = y.- LoopQuasigroupIn mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
: a unital quasigroup. Every element of S has, provably, a unique left and right inverseInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
.- Bol loopBol loopIn mathematics and abstract algebra, a Bol loop is an algebraic structure generalizing the notion of group. Bol loops are named for the Dutch mathematician Gerrit Bol who introduced them in ....
: A loop satisfying either a.b.ac = a.ba.c (left) or ca.b.a = c.ab.a (right).- Moufang loopMoufang loopIn mathematics, a Moufang loop is a special kind of algebraic structure. It is similar to a group in many ways but need not be associative. Moufang loops were introduced by Ruth Moufang.-Definition:...
: a left and right bol loopBol loopIn mathematics and abstract algebra, a Bol loop is an algebraic structure generalizing the notion of group. Bol loops are named for the Dutch mathematician Gerrit Bol who introduced them in ....
. More simply, a loop satisfying zx.yz = z.xy.z. - Bruck loopBol loopIn mathematics and abstract algebra, a Bol loop is an algebraic structure generalizing the notion of group. Bol loops are named for the Dutch mathematician Gerrit Bol who introduced them in ....
: a bol loopBol loopIn mathematics and abstract algebra, a Bol loop is an algebraic structure generalizing the notion of group. Bol loops are named for the Dutch mathematician Gerrit Bol who introduced them in ....
whose inverse satisfies (ab) = (a)(b).
- Moufang loop
- GroupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
: an associative loop.
- Bol loop
- Loop
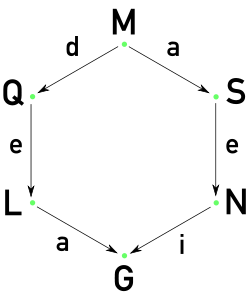
The following diagram summarizes two possible paths from magma to group.
NOTE:
- a = associativityAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, d = divisibility, e = identityIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
, i = invertibility. d and i jointly imply the cancellation propertyCancellation propertyIn mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
. - G = group, L = loop, M = magma, N = monoid, Q = quasigroup, S = semigroup.
One ternary operation
Ternary operation
In mathematics, a ternary operation is an n-ary operation with n = 3. A ternary operation on a set A takes any given three elements of A and combines them to form a single element of A. An example of a ternary operation is the product in a heap....
, heap product, denoted xyz:
- SemiheapHeap (mathematics)In abstract algebra, a heap is a mathematical generalisation of a group. Informally speaking, a heap is obtained from a group by "forgetting" which element is the unit, in the same way that an affine space can be viewed as a vector space in which the 0 element has been "forgotten"...
: S is closed under heap product, which para-associates: vwx.yz = v.wxy.z = vw.xyz.- Idempotent semiheapHeap (mathematics)In abstract algebra, a heap is a mathematical generalisation of a group. Informally speaking, a heap is obtained from a group by "forgetting" which element is the unit, in the same way that an affine space can be viewed as a vector space in which the 0 element has been "forgotten"...
: A semiheap satisfying xxx = x.- Generalized heapHeap (mathematics)In abstract algebra, a heap is a mathematical generalisation of a group. Informally speaking, a heap is obtained from a group by "forgetting" which element is the unit, in the same way that an affine space can be viewed as a vector space in which the 0 element has been "forgotten"...
: An idempotent semiheap satisfying yy.zzx = zz.yyx and xyy.zz = xzz.yy.
- Generalized heap
- HeapHeap (mathematics)In abstract algebra, a heap is a mathematical generalisation of a group. Informally speaking, a heap is obtained from a group by "forgetting" which element is the unit, in the same way that an affine space can be viewed as a vector space in which the 0 element has been "forgotten"...
: A semiheap satisfying yyx = xyy = x.- GroupHeap (mathematics)In abstract algebra, a heap is a mathematical generalisation of a group. Informally speaking, a heap is obtained from a group by "forgetting" which element is the unit, in the same way that an affine space can be viewed as a vector space in which the 0 element has been "forgotten"...
: A heap with distinguished element 1. The group product of x and y is defined as x1y, and the group inverse of x is defined as 1x1.
- Group
- Idempotent semiheap
Lattice-like structures
The binary operations meetMeet (mathematics)
In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
and join, which characterize nearly all structures in this section, are idempotent, by assumption or proof. Latticoids are the only lattice-like structure that do not associate. N.B. "Lattice" is also employed in a number of group-theoretic contexts
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
, including to refer to a discrete subgroup of the real vector space Rn that spans Rn.
Some concepts from order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
that recur in lattice theory:
- Strict partial order: A set S with a relation that is transitiveTransitive relationIn mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
and irreflexive.- Preordered set: A strict partial order that is reflexiveReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
.- Directed setDirected setIn mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
: A preordered set such that every pair of elements has an upper boundUpper boundIn mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
. - Partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
: A preordered set with the antisymmetryAntisymmetric relationIn mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
property.- Totally ordered set: A partially ordered set with totalityTotal relationIn mathematics, a binary relation R over a set X is total if for all a and b in X, a is related to b or b is related to a .In mathematical notation, this is\forall a, b \in X,\ a R b \or b R a....
replacing reflexivityReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
.
- Totally ordered set: A partially ordered set with totality
- Directed set
- Preordered set: A strict partial order that is reflexive
One binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
, one of meet
Meet (mathematics)
In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
or join, and denoted by concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
. The two structures below are also magmas
Magma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
; see the preceding section.
- SemilatticeSemilatticeIn mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
: the binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
commutes and associates. Also a partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
closed under one of pairwise greatest lower bound or least upper bound.- LatticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
: a semilattice with a unary operation, dualization, denoted by enclosure within a pair of brackets. If xy denotes meet, (xy) denotes join, and vice versa. The binary and unary operations interact via a form of the absorption lawAbsorption lawIn algebra, the absorption law or absorption identity is an identity linking a pair of binary operations.Two binary operations, say ¤ and *, are said to be connected by the absorption law if:...
, x(xy) = x = (x(xy)).
- Lattice
Two binary operations, meet
Meet (mathematics)
In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
(infix
Infix
An infix is an affix inserted inside a word stem . It contrasts with adfix, a rare term for an affix attached to the end of a stem, such as a prefix or suffix.-Indonesian:...
∧) and join (infix ∨). Duality
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
means that interchanging all meets and joins preserves truth.
- Latticoid: meet and join commuteCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
but do not associate. - Skew latticeSkew latticeIn abstract algebra, a skew lattice is an algebraic structure that is a non-commutative generalization of a lattice. While the term skew lattice can be used to refer to any non-commutative generalization of a lattice, over the past twenty years it has been used primarily as follows.-Definition:A...
: meet and join associate but do not commute. - LatticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
: a commutative skew lattice, an associative latticoid, and both a meetMeet (mathematics)In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
and join semilatticeSemilatticeIn mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
. Meet and join interact via the absorption lawAbsorption lawIn algebra, the absorption law or absorption identity is an identity linking a pair of binary operations.Two binary operations, say ¤ and *, are said to be connected by the absorption law if:...
: x∧(x∨y) = x. Also a partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
closed under pairwise greatest lower bound and least upper bound.- Bounded lattice: a lattice with two distinguished elements, the greatestGreatest elementIn mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
(1) and the least elementGreatest elementIn mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
(0), such that x∨1=1 and x∨0=x. DualizingDuality (order theory)In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
requires interchanging 0 and 1. A bounded lattice is a pointed setPointed setIn mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
.- Complete latticeComplete latticeIn mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
:- Algebraic lattice:
- Complete lattice
- Involutive lattice: a lattice with a unary operation, denoted by postfix ', and satisfying x"=x and (x∨y)' = x' ∧y' .
- Relatively complemented lattice:
- Complemented latticeComplemented latticeIn the mathematical discipline of order theory, a complemented lattice is a bounded lattice in which every element a has a complement, i.e. an element b satisfying a ∨ b = 1 and a ∧ b = 0....
: a lattice with a unary operation, complementationComplemented latticeIn the mathematical discipline of order theory, a complemented lattice is a bounded lattice in which every element a has a complement, i.e. an element b satisfying a ∨ b = 1 and a ∧ b = 0....
, denoted by postfixReverse Polish notationReverse Polish notation is a mathematical notation wherein every operator follows all of its operands, in contrast to Polish notation, which puts the operator in the prefix position. It is also known as Postfix notation and is parenthesis-free as long as operator arities are fixed...
', such that x∧x' = 0 and 1=0'. 0 and 1 bound S.- Orthocomplemented lattice: a complemented lattice satisfying x" = x and x∨y=y ↔ y' ∨x' = x' (complementation is order reversingMonotonic functionIn mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
).- Orthomodular lattice: an ortholattice such that (x ≤ y) → (x ∨ (x⊥ ∧ y) = y) holds.
- De Morgan algebraDe Morgan algebraIn mathematics, a De Morgan algebra is a structure A = such that:* is a bounded distributive lattice, and...
: a complemented lattice satisfying x" = x and (x∨y)' = x' ∧y' . Also a bounded involutive lattice.
- Orthocomplemented lattice: a complemented lattice satisfying x" = x and x∨y=y ↔ y' ∨x' = x' (complementation is order reversing
- Modular latticeModular latticeIn the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular law: x ≤ b implies x ∨ = ∧ b,where ≤ is the partial order, and ∨ and ∧ are...
: a lattice satisfying the modular identity, x∨(y∧(x∨z)) = (x∨y)∧(x∨z).- Metric lattice:
- Projective lattice:
- Arguesian lattice: a modular lattice satisfying the identity .
- Distributive latticeDistributive latticeIn mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
: a lattice in which each of meet and join distributesDistributive latticeIn mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
over the other. Distributive lattices are modular, but the converse need not hold.- Boolean algebra: a complemented distributive lattice. Either of meet or join can be defined in terms of the other and complementation.
- Boolean algebra with operators: a Boolean algebra with one or more added operations, usually unary. Let a postfix * denote any added unary operation. Then 0* = 0 and (x∨y)* = x*∨y*. More generally, all added operations (a) evaluate to 0 if any argument is 0, and (b) are join preservingLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, i.e., distribute over join.- Modal algebraModal logicModal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
: a Boolean algebra with a single added operator, the modal operatorModal operatorIn modal logic, a modal operator is an operator which forms propositions from propositions. In general, a modal operator has the "formal" property of being non-truth-functional, and is "intuitively" characterised by expressing a modal attitude about the proposition to which the operator is applied...
.- Derivative algebraDerivative algebra (abstract algebra)In abstract algebra, a derivative algebra is an algebraic structure of the signature where is a Boolean algebra and D is a unary operator, the derivative operator, satisfying the identities: # 0D = 0 # xDD ≤ x + xD...
: a modal algebra whose added unary operation, the derivative operator, satisfies x**∨x*∨x = x*∨x. - Interior algebraInterior algebraIn abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic...
: a modal algebra whose added unary operation, the interior operator, satisfies x*∨x = x and x** = x*. The dual is a closure algebra.- Monadic Boolean algebraMonadic Boolean algebraIn abstract algebra, a monadic Boolean algebra is an algebraic structure with signaturewhere ⟨A, ·, +, ', 0, 1⟩ is a Boolean algebra.The prefixed unary operator ∃ denotes the existential quantifier, which satisfies the identities:...
: a closure algebra whose added unary operation, the existential quantifier, denoted by prefix ∃, satisfies the axiom ∃(∃x)' = (∃x)'. The dual operator, ∀x := (∃x' )' is the universal quantifier.
- Monadic Boolean algebra
- Derivative algebra
- Modal algebra
- Boolean algebra with operators: a Boolean algebra with one or more added operations, usually unary. Let a postfix * denote any added unary operation. Then 0* = 0 and (x∨y)* = x*∨y*. More generally, all added operations (a) evaluate to 0 if any argument is 0, and (b) are join preserving
- Boolean algebra: a complemented distributive lattice. Either of meet or join can be defined in terms of the other and complementation.
- Bounded lattice: a lattice with two distinguished elements, the greatest
-
-
-
- Three structures whose intended interpretations are first order logic:
- Polyadic algebraPolyadic algebraPolyadic algebras are algebraic structures introduced by Paul Halmos. They are related to first-order logic in a way analogous to the relationship between Boolean algebras and propositional logic .There are other ways to relate first-order logic to algebra, including Tarski's cylindric algebras...
: a monadic Boolean algebraMonadic Boolean algebraIn abstract algebra, a monadic Boolean algebra is an algebraic structure with signaturewhere ⟨A, ·, +, ', 0, 1⟩ is a Boolean algebra.The prefixed unary operator ∃ denotes the existential quantifier, which satisfies the identities:...
with a second unary operation, denoted by prefixed S. I is an index setIndex setIn mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
, J,K⊂I. ∃ maps each J into the quantifier ∃(J). S maps I→I transformations into Boolean endomorphismEndomorphismIn mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s on S. σ, τ range over possible transformations; δ is the identity transformation. The axioms are: ∃(∅)a=a, ∃(J∪K) = ∃(J)∃(K), S(δ)a = a, S(σ)S(τ) = S(στ), S(σ)∃(J) = S(τ)∃(J) (∀i∈I-J, such that σi=τi), and ∃(J)S(τ) = S(τ)∃(τ-1J) (τ injective). - Relation algebraRelation algebraIn mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
: S, the Cartesian square of some set, is a:
-
- Boolean algebra under join and complementation;
- MonoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under binary composition (infix •) and the identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
I such that 1=I '∨I; - Residuated Boolean algebraResiduated Boolean algebraIn mathematics, a residuated Boolean algebra is a residuated lattice whose lattice structure is that of a Boolean algebra. Examples include Boolean algebras with the monoid taken to be conjunction, the set of all formal languages over a given alphabet Σ under concatenation, the set of all binary...
by virtue of a second unary operation, converseInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
(postfix ) and the axiom (A
) and the axiom (A •(A•B)')∨B ' = B '.
•(A•B)')∨B ' = B '.
- Converse is an involution and distributes over composition so that (A•B)
 = B
= B •A
•A . Converse and composition each distribute over join.
. Converse and composition each distribute over join.
- Cylindric algebraCylindric algebraThe notion of cylindric algebra, invented by Alfred Tarski, arises naturally in the algebraization of first-order logic with equality. This is comparable to the role Boolean algebras play for propositional logic. Indeed, cylindric algebras are Boolean algebras equipped with additional...
: Boolean algebra augmented by unary cylindrification operations.
- Polyadic algebra
- Three structures whose intended interpretations are first order logic:
-
-
Three binary operations:
-
-
-
- Boolean semigroup: a Boolean algebra with an added binary operation that associates, distributes over join, and is annihilated by 0.
- Implicative lattice: a distributive lattice with a third binary operation, implication, that distributes left and right over each of meet and join.
- Brouwerian algebra: a distributive lattice with a greatest elementGreatest elementIn mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
and a third binary operation, denoted by infix " ' ", satisfying ((x∧y)≤z)∧(y≤x)' z.
-
- Heyting algebraHeyting algebraIn mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
: a Brouwerian algebra with a least element, whose third binary operation, now called relative pseudo-complement, satisfies the identities x'x=1, x(x'y) = xy, x' (yz) = (x'y)(x'z), and (xy)z = (x'z)(y'z). In pointless topologyPointless topologyIn mathematics, pointless topology is an approach to topology that avoids mentioning points. The name 'pointless topology' is due to John von Neumann...
, a Heyting algebra is called a frame.
- Heyting algebra
-
-
Four or more binary operations:
- Residuated semilattice: a semilattice under meet or join, a monoid under product, and two further binary operations, residuation, satisfying the axioms .
- Action algebraAction algebraIn algebraic logic, an action algebra is an algebraic structure which is both a residuated semilattice and a Kleene algebra. It adds the star or reflexive transitive closure operation of the latter to the former, while adding the left and right residuation or implication operations of the former...
: a residuated semilattice that is also Kleene latticeKleene algebraIn mathematics, a Kleene algebra is either of two different things:* A bounded distributive lattice with an involution satisfying De Morgan's laws , additionally satisfying the inequality x∧−x ≤ y∨−y. Kleene algebras are subclasses of Ockham algebras...
. Hence combines a 〈∨, •, 1, ←, →〉 algebra with a 〈∨, 0, •, 1, *〉 algebra. - Residuated latticeResiduated latticeIn abstract algebra, a residuated lattice is an algebraic structure that is simultaneously a lattice x ≤ y and a monoid x•y which admits operations x\z and z/y loosely analogous to division or implication when x•y is viewed as multiplication or conjunction respectively...
: a Brouwerian algebra with a least element and a fourth binary operation, denoted by infix ⊗, such that (⊗,1) is a commutative monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
obeying the adjointness property ((x≤y)' z) ↔ (x⊗y≤z).- Residuated Boolean algebraResiduated Boolean algebraIn mathematics, a residuated Boolean algebra is a residuated lattice whose lattice structure is that of a Boolean algebra. Examples include Boolean algebras with the monoid taken to be conjunction, the set of all formal languages over a given alphabet Σ under concatenation, the set of all binary...
: a residuated latticeResiduated latticeIn abstract algebra, a residuated lattice is an algebraic structure that is simultaneously a lattice x ≤ y and a monoid x•y which admits operations x\z and z/y loosely analogous to division or implication when x•y is viewed as multiplication or conjunction respectively...
whose lattice part is a Boolean algebra.- Relation algebraRelation algebraIn mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
: a residuated Boolean algebraResiduated Boolean algebraIn mathematics, a residuated Boolean algebra is a residuated lattice whose lattice structure is that of a Boolean algebra. Examples include Boolean algebras with the monoid taken to be conjunction, the set of all formal languages over a given alphabet Σ under concatenation, the set of all binary...
with an added unary operation, converseInverse relationIn mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
.
- Relation algebra
MonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under an added residuatedResiduated latticeIn abstract algebra, a residuated lattice is an algebraic structure that is simultaneously a lattice x ≤ y and a monoid x•y which admits operations x\z and z/y loosely analogous to division or implication when x•y is viewed as multiplication or conjunction respectively...
binary operation, composition with identity element I, such that 1=I '∨I. Composition and converse distribute over join. A B = (A '⊗B ')' defines a 4th binary operation, relational addition.
B = (A '⊗B ')' defines a 4th binary operation, relational addition. - Residuated Boolean algebra
- Action algebra
The following Hasse diagram
Hasse diagram
In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
illustrates some pathways from a very general concept, partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s, to the oldest and most researched lattice, Boolean algebra. This diagram reveals some of the hierarchical structure linking a number of important types of lattices, not all discussed above because some are not varieties. This diagram consists of a number of links of the form A→B, each meaning that structure A is included in structure B.

Lattice ordered structures
S includes distinguished elements and is closed under additional operations, so that the axioms for a semigroupSemigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
, monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
, group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, or a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
are satisfied.
Ring-like structures
Two binary operations, addition and multiplication. That multiplication has a 0 is either an axiom or a theorem.- Shell: MultiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
has left/right identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of 1, and a zero elementAbsorbing elementIn mathematics, an absorbing element is a special type of element of a set with respect to a binary operation on that set. The result of combining an absorbing element with any element of the set is the absorbing element itself. In semigroup theory, the absorbing element is called a zero element...
, 0, which is also the left/right identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
for additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
. - Ringoid: multiplication distributes over addition.
- Nonassociative ringNonassociative ringIn abstract algebra, a nonassociative ring is a generalization of the concept of ring.A nonassociative ring is a set R with two operations, addition and multiplication, such that:# R is an abelian group under addition:## a+b = b+a...
: a ringoid that is an abelian group under addition.- Lie ringLie ringIn mathematics a Lie ring is a structure related to Lie algebras that can arise as a generalisation of Lie algebras, or through the study of the lower central series of groups.- Formal definition :...
: a nonassociative ring whose multiplication anticommutes and satisfies the Jacobi identityJacobi identityIn mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
. - Jordan ring: a nonassociative ring whose multiplication commutes and satisfies the Jordan identity.
- Lie ring
- Newman algebra: a ringoid that is also a shell. There is a unary operation, inverse, denoted by a postfix "'", such that x+x'=1 and xx'=0. The following are provable: inverse is unique, x"=x, addition commutes and associates, and multiplication commutes and is idempotent.
- SemiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
: a ringoid that is also a shell. Addition and multiplication associate, addition commutes.- Commutative semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
: a semiring whose multiplication commutes.
- Commutative semiring
- RngRng (algebra)In abstract algebra, a rng is an algebraic structure satisfying the same properties as a ring, except that multiplication need not have an identity element...
: a ringoid that is an Abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition and 0, and a semigroup under multiplication.- RingRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
: a rng that is a monoid under multiplication and 1.- Commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
: a ring with commutative multiplication.- Boolean ringBoolean ringIn mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
: a commutative ring with idempotent multiplication, isomorphic to Boolean algebra.
- Boolean ring
- Differential ringDifferential algebraIn mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
: A ring with an added unary operationUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
, derivationDifferential algebraIn mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
, denoted by prefixSuffixIn linguistics, a suffix is an affix which is placed after the stem of a word. Common examples are case endings, which indicate the grammatical case of nouns or adjectives, and verb endings, which form the conjugation of verbs...
∂ and satisfying the product ruleProduct ruleIn calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
, ∂(xy) = ∂xy+x∂y.
- Commutative ring
- Ring
- Nonassociative ring
N.B. The above definitions of rng, ring, and semiring do not command universal assent:
- Some employ "ring" to denote what is here called a rngRng (algebra)In abstract algebra, a rng is an algebraic structure satisfying the same properties as a ring, except that multiplication need not have an identity element...
, and call a ring in the above sense a "ring with identity"; - Some define a semiring as having no identity elements.
Modules and algebras
These structures feature a set R whose elements are scalarsScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
, denoted by Greek letters, and a set S whose members are denoted by Latin letters. For every ring R, there is a corresponding variety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
of R-modules.
R is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and S is a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
.
- Group ringGroup ringIn algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
: a monoid ring such that
- Group algebraGroup algebraIn mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
: a group ring whose group product commutes.
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
:
Group with operators
In abstract algebra, a branch of pure mathematics, the algebraic structure group with operators or Ω-group is a group with a set of group endomorphisms.Groups with operators were extensively studied by Emmy Noether and her school in the 1920s...
, each unary operator indexed by R. The operators are scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
RxS→S, which commutes, associates, is unital, and distributes over module and scalar addition. If only the pre(post)multiplication of module elements by scalars is defined, the result is a left (right) module.
- ComoduleComoduleIn mathematics, a comodule or corepresentation is a concept dual to a module. The definition of a comodule over a coalgebra is formed by dualizing the definition of a module over an associative algebra.-Formal definition:...
: the dualDual (category theory)In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
of a module. - Vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
: A module such that
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. There is a second binary operation over S, called multiplication and denoted by concatenation, which distributes over module addition and is bilinear: α(xy) = (αx)y = x(αy).
- Algebra over a fieldAlgebra over a fieldIn mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
: An algebra over a ring whose
- Associative algebraAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
: an algebra over a field or ring, whose vector multiplication associates.- CoalgebraCoalgebraIn mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
: the dualDual (category theory)In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
of a unital associative algebra. - Commutative algebraCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
: an associative algebra whose vector multiplication commutes. - Incidence algebraIncidence algebraIn order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
: an associative algebra such that the elements of
- Coalgebra
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of functions.
Jordan algebra
In abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
: an algebra over a field whose vector multiplication commutes, may or may not associate, and satisfies the Jordan identity.
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
: an algebra over a field satisfying the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
. The vector multiplication, the Lie bracket
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
denoted [u,v], anticommutes, usually does not associate, and is nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
.
- Kac-Moody algebra: a Lie algebra, usually infinite-dimensional, definable by generators and relations through a generalized Cartan matrix.
- Generalized Kac-Moody algebra: a Kac-Moody algebra whose simple roots may be imaginaryImaginary numberAn imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
. - Affine Lie algebraAffine Lie algebraIn mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra for which the generalized Cartan matrix is positive semi-definite and has corank 1...
: a Kac-Moody algebra whose generalized Cartan matrix is positive semi-definite and has corank 1.
- Generalized Kac-Moody algebra: a Kac-Moody algebra whose simple roots may be imaginary
Quasivarieties
A quasivarietyQuasivariety
In mathematics, a quasivariety is a class of algebraic structures generalizing the notion of variety by allowing equational conditions on the axioms defining the class.-Definition:...
is a variety with one or more axioms that are quasiidentities
Quasiidentity
In universal algebra, a quasiidentity is an implication of the formwhere s1, ..., sn, s and t1, ..., tn,t are terms built up from variables using the operation symbols of the specified signature....
. Let Greek letters be metavariables denoting identities
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
. A quasiidentity then takes the form (α1∧,...,∧αn) → β.
Magmas
A magmaMagma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
(sometimes called "groupoid", or "algebra of type (2)") is a set equipped with a binary operation.
Cancellative
- SemigroupCancellation propertyIn mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
: a semigroup satisfying the added axioms
Cancellation property
In mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
: a unital cancellative semigroup.
Combinatory logic
The elements of S are higher order functions, and concatenation denotes the binary operation of function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
.
- BCI algebra: a magma with distinguished element 0, satisfying the identities (
- BCK algebraBCK algebraIn mathematics, BCI and BCK algebras are algebraic structures, introduced by Y. Imai, K. Iséki and S. Tanaka in 1966, that describe fragments of the propositional calculus involving implication known as BCI and BCK logics.-BCI algebra:An algebra \leftIn mathematics, BCI and BCK algebras are...
: a BCI algebra satisfying the identity
SKI combinator calculus
SKI combinator calculus is a computational system that may be perceived as a reduced version of untyped lambda calculus. It can be thought of as a computer programming language, though it is not useful for writing software...
: A combinator concatenates upper case letters. Terms
Term (mathematics)
A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
concatenate combinators and lower case letters. Concatenation is left and right cancellative
Cancellation property
In mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
. '=' is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
over terms. The axioms are Sxyz
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
.
- Extensional combinatory logicCombinatory logicCombinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
: Combinatory logic with the added quasiidentity (
Graphs
One set, V a finite set of verticesVertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
, and a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
E⊆V2, adjacency, consisting of edges. No operations.
- Directed graphDirected graphA directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
:
- Graph algebraGraph algebraIn mathematics, especially in the fields of universal algebra and graph theory, a graph algebra is a way of giving a directed graph an algebraic structure. It was introduced in , and has seen many uses in the field of universal algebra since then....
: - Directed acyclic graphDirected acyclic graphIn mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
: A directed graph with no pathPath (graph theory)In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
whose endpoints are the same element of
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
: A directed graph such that
Loop (graph theory)
In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....
possible.
- Connected graph: A graph such that a pathPath (graph theory)In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
connects any two vertices.- TreeTree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
: a connected graph with no cyclesCycle (graph theory)In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
. - Cycle graphCycle graphIn graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
: a connected graph consisting of a single cycleCycle (graph theory)In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
. - Complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
: a connected graph such that the shortest path between any two vertices includes no other vertex. Hence for any two vertices x and y, (x,y) and (y,x) are both elements of E.- TournamentTournament (graph theory)A tournament is a directed graph obtained by assigning a direction for each edge in an undirected complete graph. That is, it is a directed graph in which every pair of vertices is connected by a single directed edge....
: A complete graph such that only one of (
- Tournament
- Tree
Lattices
- Semimodular latticeSemimodular latticeIn the branch of mathematics known as order theory, a semimodular lattice, is a lattice that satisfies the following condition:Semimodular law: a ∧ b ...
: - Kleene latticeKleene algebraIn mathematics, a Kleene algebra is either of two different things:* A bounded distributive lattice with an involution satisfying De Morgan's laws , additionally satisfying the inequality x∧−x ≤ y∨−y. Kleene algebras are subclasses of Ockham algebras...
: a bounded distributive lattice with a unary involution, denoted by postfix ', satisfying the axioms (x∨y)' = x'∨y', x" = x, and (x∧x')∨(y∨y') = y∨y'. - Semidistributive lattice: a lattice satisfying the axiom (x∧y = x∧z)→(x∧y=x∧(y∨z)), and dually.
Ring-like
- Kleene algebraKleene algebraIn mathematics, a Kleene algebra is either of two different things:* A bounded distributive lattice with an involution satisfying De Morgan's laws , additionally satisfying the inequality x∧−x ≤ y∨−y. Kleene algebras are subclasses of Ockham algebras...
: a semiring with idempotent addition and a unary operation, the Kleene starKleene starIn mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
, denoted by postfixReverse Polish notationReverse Polish notation is a mathematical notation wherein every operator follows all of its operands, in contrast to Polish notation, which puts the operator in the prefix position. It is also known as Postfix notation and is parenthesis-free as long as operator arities are fixed...
* and satisfying (1+x*x)x*=x*=(1+xx*)x*.
Universal classes
- Quasitrivial groupoidGroupoidIn mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
: a magmaMagmaMagma is a mixture of molten rock, volatiles and solids that is found beneath the surface of the Earth, and is expected to exist on other terrestrial planets. Besides molten rock, magma may also contain suspended crystals and dissolved gas and sometimes also gas bubbles. Magma often collects in...
such that xy = x or y.
- Integral domain: A commutative ring such that (xy=0)→((x=0)∨(y=0)). Also a domainDomain (ring theory)In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
whose multiplication commutes. - Integral relation algebra: a relation algebraRelation algebraIn mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
such that (xy=0)→((x=0)∨(y=0)).
Partial order for nonlattices
If the partial order relation ≤ is added to a structure other than a lattice, the result is a partially ordered structure. These are discussed in Birkhoff (1967: chpts. 13-15, 17) using a differing terminology. Examples include:- Ordered magmaMagma (algebra)In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
, semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
, monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
, groupOrdered groupIn abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
, and vector spaceOrdered vector spaceIn mathematics an ordered vector space or partially ordered vector space is a vector space equipped with a partial order which is compatible with the vector space operations.- Definition:...
: In each case,
Linearly ordered group
In abstract algebra a linearly ordered or totally ordered group is an ordered group G such that the order relation "≤" is total...
and ordered ring
Ordered ring
In abstract algebra, an ordered ring is a commutative ring R with a total order ≤ such that for all a, b, and c in R:* if a ≤ b then a + c ≤ b + c.* if 0 ≤ a and 0 ≤ b then 0 ≤ ab....
:
- Archimedean groupArchimedean groupIn abstract algebra, a branch of mathematics, an Archimedean group is an algebraic structure consisting of a set together with a binary operation and binary relation satisfying certain axioms detailed below. We can also say that an Archimedean group is a linearly ordered group for which the...
: a linearly ordered groupLinearly ordered groupIn abstract algebra a linearly ordered or totally ordered group is an ordered group G such that the order relation "≤" is total...
for which the Archimedean propertyArchimedean propertyIn abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
holds.
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
: a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
whose
Nonvarieties
Nonvarieties cannot be axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
atized solely with identities
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
and quasiidentities
Quasiidentity
In universal algebra, a quasiidentity is an implication of the formwhere s1, ..., sn, s and t1, ..., tn,t are terms built up from variables using the operation symbols of the specified signature....
. Many nonidentities are of three very simple kinds:
- The requirement that
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, namely one such that S≠{0}, 0 being the additive identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. The nearest thing to an identity implying S≠{0} is the nonidentity 0≠1, which requires that the additive and multiplicative identities be distinct.
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of each operation must be an entire underlying set; there can be no partial operations.
Most of the classic results of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
do not hold for nonvarieties. For example, neither the free field
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
over any set nor the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of integral domains exists. Nevertheless, nonvarieties often retain an undoubted algebraic flavor.
There are whole classes of axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
atic formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
s not included in this section, e.g., logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
s, topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, and this exclusion is in some sense arbitrary. Many of the nonvarieties below were included because of their intrinsic interest and importance, either by virtue of their foundational nature (Peano arithmetic), ubiquity (the real field
Formally real field
In mathematics, in particular in field theory and real algebra, a formally real field is a field that admits an ordering which makes it an ordered field.-Alternative Definitions:...
), or richness (e.g., fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, normed vector spaces). Also, a great deal of theoretical physics can be recast using the nonvarieties called multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
s.
No operations. Functions or relations may be present:
- MultisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
: S is a multiset and
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s. There is a multifunction
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
m: S→N such that m(x) is the multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
of x∈S.
Arithmetics
If the name of a structure in this section includes the word "arithmetic," the structure features one or both of the binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
. If both operations are included, the recursive identity defining multiplication usually links them. Arithmetics necessarily have infinite models
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
.
- Cegielski arithmetic: A commutative cancellative monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under multiplication. 0 annihilates multiplication, and xy=1 if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
x and y are both 1. Other axioms and one axiom schema govern order, exponentiationExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
, divisibility, and primality; consult Smorynski. Adding the successor function and its axioms as per Dedekind algebra render addition recursively definable, resulting in a system with the expressive power of Robinson arithmeticRobinson arithmeticIn mathematics, Robinson arithmetic, or Q, is a finitely axiomatized fragment of Peano arithmetic , first set out in R. M. Robinson . Q is essentially PA without the axiom schema of induction. Since Q is weaker than PA, it is incomplete...
.
In the structures below, addition and multiplication, if present, are recursively
Recursive definition
In mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
defined by means of an injective operation called successor, denoted by prefix σ. 0 is the axiomatic identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
for addition, and annihilates multiplication. Both axioms hold for semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
s.
- Dedekind algebra, also called a Peano algebra: A pointed unary system by virtue of 0, the unique element of S not included in the rangeRange (mathematics)In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of successor. Dedekind algebras are fragments of Skolem arithmetic.- Dedekind-Peano structurePeano axiomsIn mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
: A Dedekind algebra with an axiom schemaAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
of inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
.- Presburger arithmeticPresburger arithmeticPresburger arithmetic is the first-order theory of the natural numbers with addition, named in honor of Mojżesz Presburger, who introduced it in 1929. The signature of Presburger arithmetic contains only the addition operation and equality, omitting the multiplication operation entirely...
: A Dedekind-Peano structure with recursiveRecursive definitionIn mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
.
- Presburger arithmetic
- Dedekind-Peano structure
Arithmetics above this line are decidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
. Those below are incompletable.
-
-
- Robinson arithmeticRobinson arithmeticIn mathematics, Robinson arithmetic, or Q, is a finitely axiomatized fragment of Peano arithmetic , first set out in R. M. Robinson . Q is essentially PA without the axiom schema of induction. Since Q is weaker than PA, it is incomplete...
: Presburger arithmetic with recursiveRecursive definitionIn mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
.
-
- Peano arithmetic: Robinson arithmetic with an axiom schemaAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
of inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. The semiring axioms for
- Peano arithmetic: Robinson arithmetic with an axiom schema
- Robinson arithmetic
-
-
- Heyting arithmeticHeyting arithmeticIn mathematical logic, Heyting arithmetic is an axiomatization of arithmetic in accordance with the philosophy of intuitionism. It is named after Arend Heyting, who first proposed it....
: Peano arithmetic with intuitionist logic as the background logic.
- Heyting arithmetic
-
- Primitive recursive arithmeticPrimitive recursive arithmeticPrimitive recursive arithmetic, or PRA, is a quantifier-free formalization of the natural numbers. It was first proposed by Skolem as a formalization of his finitist conception of the foundations of arithmetic, and it is widely agreed that all reasoning of PRA is finitist...
: A Dedekind algebra with recursively defined addition, multiplication, exponentiation, and other primitive recursive operations as desired. A rule of induction replaces the axiom of induction. The background logic lacks quantificationQuantificationQuantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
and thus is not first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. - Skolem arithmetic (Boolos and Jeffrey 2002: 73-76): Not an algebraic structure because there is no fixed set of operations of fixed adicityArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
. Skolem arithmetic is a Dedekind algebra with projection functionsProjection (mathematics)Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
, indexed by n, whose arguments are functions and that return the nth argument of a function. The identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
is the projection function whose arguments are all unary operations. Composite operations of any adicity, including addition and multiplication, may be constructed using function compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
and primitive recursion. Mathematical inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
becomes a theorem.- Kalmar arithmetic: Skolem arithmetic with different primitive functions.
- Primitive recursive arithmetic
The following arithmetics lack a connection between addition and multiplication. They are the simplest arithmetics capable of expressing all primitive recursive function
Primitive recursive function
The primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
s.
- Baby Arithmetic: Because there is no universal quantificationUniversal quantificationIn predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
, there are axiom schemesAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
but no axioms. [n] denotes n consecutive applications of successor to 0. Addition and multiplication are defined by the schemes [n]+[p] = [n+p] and [n][p] = [np].Binary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
s "=" and "≤". These relations are governed by the schemes [n]=[p] ↔ n=p, (x≤[n])→(x=0)∨,...,∨(x=[n]), and (x≤[n])∨([n]≤x).
Lattices that are not varieties
- Part algebraMereologyIn philosophy and mathematical logic, mereology treats parts and the wholes they form...
: a Boolean algebra with no least element 0, so that the complement of 1 is not defined.
Two sets, Φ and D.
- Information algebraInformation algebraClassical information theory goes back to Claude Shannon. It is a theory of information transmission, looking at communication and storage. However, it has not been considered so far that information comes from different sources and that it is therefore usually combined...
:
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under combination, an idempotent operation. The operation of focussing, f: ΦxD→Φ satisfies the axiom f(f(φ,x),y)=f(φ,x∧y) and distributes over combination. Every element of Φ has an identity element in D under focussing.
Field-like structures
Two binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s, addition and multiplication. S is nontrivial, i.e., S≠{0}. S-0 is S with 0 removed.
- DomainDomain (ring theory)In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
: a ring whose sole zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
is 0. - Integral domain: a commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, 0 ≠ 1, and having the zero-product propertyZero-product propertyIn the mathematical areas of algebra and analysis, the zero-product property, generally known as the nonexistence of zero divisors, and also called the zero-product rule, the rule of zero product, or any other similar name, is an abstract and explicit statement of the familiar property from...
: (
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s.
- Integrally closed domainIntegrally closed domainIn commutative algebra, an integrally closed domain A is an integral domain whose integral closure in the field of fractions of A is A itself...
- Unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
: an integral domain in which every nonzero element can be written as a product of a unit and prime elements of
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
: an integral domain in which every ideal is principal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
, i.e., can be generated by a single element.
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
: an integral domain with a function
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
.
- Division ringDivision ringIn abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
(also
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under multiplication.
- FieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
: a division ring whose multiplication commutes. Recapitulating:
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
over addition. x0 = 0 is a theorem.
- Algebraically closed fieldAlgebraically closed fieldIn mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
: a field such that all polynomial equations whose coefficients are elements of
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
: a field whose
- Real closed fieldReal closed fieldIn mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
: an ordered real field such that for every element
Formally real field
In mathematics, in particular in field theory and real algebra, a formally real field is a field that admits an ordering which makes it an ordered field.-Alternative Definitions:...
: a Dedekind complete ordered field.
- Differential field: A real field with an added unary operationUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
, derivationDifferential algebraIn mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
, denoted by prefix ∂, distributing over additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, ∂(
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
, ∂(xy) = ∂xy + x∂y.
The following field-like structures are not varieties for reasons in addition to S≠{0}:
- Simple ringSimple ringIn abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
: a ring having no idealsIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
other than 0 and
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
: a ring whose ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
satisfy the descending chain condition.
Vector spaces that are not varieties
The following composite structures are extensions of vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s that are not varieties. Two sets: M is a set of vectors and R is a set of scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
s.
Three binary operations.
- Normed vector spaceNormed vector spaceIn mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
: a vector space with a normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
, namely a function
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, and positive definite
Definite bilinear form
In mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
.
- Inner product spaceInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
(also
Formally real field
In mathematics, in particular in field theory and real algebra, a formally real field is a field that admits an ordering which makes it an ordered field.-Alternative Definitions:...
, whose norm is the square root of the inner product, M×M→R. Let i,j, and n be positive integers such that 1≤i,j≤n. Then M has an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
such that ei•ej = 1 if i=j and 0 otherwise. See free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
.
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
: Differs from inner product spaces in that
Conjugate (algebra)
In algebra, a conjugate of an element in a quadratic extension field of a field K is its image under the unique non-identity automorphism of the extended field that fixes K. If the extension is generated by a square root of an element...
symmetric, bilinear, and positive definite
Definite bilinear form
In mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
.
Graded vector space
In mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
: a vector space such that the members of
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
below.
Structures that build on the notion of vector space:
- MatroidMatroidIn combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
: - AntimatroidAntimatroidIn mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included...
:
Multilinear algebras
Four binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s. Two sets, V and K:
- The members of
Multivector
In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...
s (including vectors
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
), denoted by lower case Latin letters. V is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under multivector
Multivector
In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...
addition, and a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under outer product
Outer product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
. The outer product goes under various names, and is multilinear
Tensor (intrinsic definition)
In mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multi-linear concept...
in principle but usually bilinear. The outer product defines the multivectors recursively starting from the vectors. Thus the members of V have a "degree" (see graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
below). Multivectors may have an inner product as well, denoted u•v: V×V→K, that is symmetric, linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, and positive definite
Definite bilinear form
In mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
; see inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
above.
Formally real field
In mathematics, in particular in field theory and real algebra, a formally real field is a field that admits an ordering which makes it an ordered field.-Alternative Definitions:...
, as multilinear algebras are designed to describe physical phenomena without complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
of scalars and multivectors,
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
scalar multiplication.
- Symmetric algebraSymmetric algebraIn mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
: a unital commutative algebra with vector multiplication. - Universal enveloping algebraUniversal enveloping algebraIn mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
: Given a Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
A, such that the Lie algebra AL contains L.
- Hopf algebraHopf algebraIn mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
:- Group Hopf algebraGroup Hopf algebraIn mathematics, the group Hopf algebra of a given group is a certain construct related to the symmetries of group actions. Deformations of group Hopf algebras are foundational in the theory of quantum groups.-Definition:...
:
- Group Hopf algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
: an associative algebra with unital outer product. The members of
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition.
- Tensor algebraTensor algebraIn mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
: A graded algebra such that
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
. All multilinear algebras can be seen as special cases of tensor algebra.
- Exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
(also
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
. v1 ∧ v2 ∧ ... ∧ vk = 0 if and only if v1, ..., vk are linearly dependent. Multivectors also have an inner product.
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
: an exterior algebra with a symmetric bilinear form
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
: an exterior algebra whose exterior (called
- Grassmann-Cayley algebraGrassmann-Cayley algebraGrassmann–Cayley algebra, also known as double algebra, is a form of modeling algebra for use in projective geometry. The technique is based on work by German mathematician Hermann Grassmann on exterior algebra, and subsequently by British mathematician Arthur Cayley's work on matrices and linear...
: a geometric algebra without an inner product.
Structures with topologies or manifolds
These algebraic structures are not varieties, because the underlying set either has a topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
or is a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, characteristics that are not algebraic in nature. This added structure must be compatible in some sense, however, with the algebraic structure. The case of when the added structure is partial order is discussed above, under varieties.
Topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
:
- Topological groupTopological groupIn mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
: a group whose S has a topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
;- Discrete groupDiscrete groupIn mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
: a topological group whose topology is discrete. Also a 0-dimensional Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
.
- Discrete group
- Topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
: a normed vector spaceNormed vector spaceIn mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
whose R has a topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
Manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
:
- Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
: a group whose S has a smooth manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
structure.
Categories
Let there be two classes:- O whose elements are objectsCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, and - M whose elements are morphismMorphismIn mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s defined over O.
Let x and y be any two elements of M. Then there exist:
- Two functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
,
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
.
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
over
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
and denoted by concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
. xy is defined iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
c(x)=d(y). If xy is defined, d(xy) = d(x) and c(xy) = c(y).
Category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
: Composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
associates (if defined), and x has left
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
and right identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
elements, the domain and codomain of x, respectively, so that d(x)x = x = xc(x). Letting φ stand for one of c or d, and γ stand for the other, then φ(γ(x)) = γ(x).
If O has but one element, the associated category is a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
.
- GroupoidGroupoidIn mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
: Two equivalent definitions.
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
. Equivalently, a category such that every element x of M, x(a,b), has an inverse x(b,a); see diagram in section 2.2. Algebraic definition: A group whose product is a partial function
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
. Group product associates in that if ab and bc are both defined, then ab.c=a.bc. (a)a and a(a) are always defined. Also, ab.(b) = a, and (a).ab = b.
Unclassified
- Incidence algebraIncidence algebraIn order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
: An associative algebraAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
, defined for any locally finite poset and commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with unity. Part of order theoryOrder theoryOrder theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
. - Group ringGroup ringIn algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
:- Group algebraGroup algebraIn mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
:
- Group algebra
- Path algebra: related to a quiverQuiverA quiver is a container for arrows. Quivers have been traditionally made of leather, bark, wood, furs and other natural materials; modern quivers are often made of metal and plastic....
and a directed graphDirected graphA directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
. - Categorical algebraCategorical algebraIn category theory, a field of mathematics, a categorical algebra is an associative algebra, defined for any locally finite category and commutative ring with unity.It generalizes the notions of group algebra and incidence algebra,...
: an associative algebraAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
defined for any locally finite category and commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with unity. Generalizes group algebraGroup algebraIn mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
and incidence algebraIncidence algebraIn order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
, as the concept of categoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
generalizes groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and poset.
Examples
Recurring underlying sets: N=natural numbers; Z=integers; Q=rational numbers; R=real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s; C=complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Arithmetics
Free algebra
In mathematics, especially in the area of abstract algebra known as ring theory, a free algebra is the noncommutative analogue of a polynomial ring .-Definition:...
on zero generators
Generating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
of type 〈1,0〉. Freeness implies that no two terms are equal. Very general results from the theory of free algebras, e.g., definition by recursion, and uniqueness up to isomorphism, are now applicable.
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
is a free object
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
with one generator
Generating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
.
Universe (mathematics)
In mathematics, and particularly in set theory and the foundations of mathematics, a universe is a class that contains all the entities one wishes to consider in a given situation...
of singletons forms a Dedekind-Peano structure
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
if {x} interprets the successor of x, and the null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
interprets 0.
Group-like structures
- Nonzero N under additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
is a magmaMagma (algebra)In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
. - Z under subtractionSubtractionIn arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
(−) is a quasigroupQuasigroupIn mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
. - Nonzero Q under divisionDivision (mathematics)right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
(÷) is a quasigroupQuasigroupIn mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
. - Z under addition (+) is an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. - Nonzero Q under multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
(×) is an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. - Every cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
G is abelian, because if x, y are in G, then xy = aman = am+n = an+m = anam = yx. In particular, Z is an abelian group under addition, as are the integers modulo nModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, Z/nZ. - Every group is a loop, because a*x = b if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
x = a−1*b, and y*a = b if and only if y = b*a−1. - Invertible 2x2 matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
form a group under matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. - The permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s preserving the partition of a setPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
induced by an equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
form a group under function compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
and inverseInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
. - MV-algebraMV-algebraIn abstract algebra, a branch of pure mathematics, an MV-algebra is an algebraic structure with a binary operation \oplus, a unary operation \neg, and the constant 0, satisfying certain axioms...
s characterize multi-valuedMulti-valued logicIn logic, a many-valued logic is a propositional calculus in which there are more than two truth values. Traditionally, in Aristotle's logical calculus, there were only two possible values for any proposition...
and fuzzy logicFuzzy logicFuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
s.
- The set of all functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
X→X, X any nonempty set, is a monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under function compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
and the identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
. - In category theoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the set of all endomorphismEndomorphismIn mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s of object X in categoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
C is a monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under composition of morphismsFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
and the identity morphism.
Also see examples of groups
Examples of groups
Some elementary examples of groups in mathematics are given on Group .Further examples are listed here.-Permutations of a set of three elements:Consider three colored blocks , initially placed in the order RGB...
, list of small groups, and list of finite simple groups.
Lattices
- The following structures, if ordered by set inclusion, all form modular latticeModular latticeIn the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular law: x ≤ b implies x ∨ = ∧ b,where ≤ is the partial order, and ∨ and ∧ are...
s. The:- SubgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, normal or not; - SubringSubringIn mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
s and idealsIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
; - Submodules of a moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
and the subspaceLinear subspaceThe concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
s of a vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
; - Equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s on any set; - SublatticesLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
of any lattice including the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
.
- Subgroup
- The closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s of a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
form a lattice under finite unionsUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
and intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
s. The open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s, ordered by inclusion, form a lattice under arbitrary unions. - A Boolean algebra (BA) is also an ortholattice, a Boolean ringBoolean ringIn mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
, a commutative monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
, and a Newman algebra. The BA 2 is a boundary algebraLaws of FormLaws of Form is a book by G. Spencer-Brown, published in 1969, that straddles the boundary between mathematics and philosophy...
. A BA would be an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
if (b)ba = a were a BA identity. - Any field of sets, and the connectiveLogical connectiveIn logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
s of first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, are models of Boolean algebra. See Lindenbaum-Tarski algebra. - The connectives of intuitionistic logicIntuitionistic logicIntuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
form a model of Heyting algebraHeyting algebraIn mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
. - The modal logicModal logicModal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
s KNormal modal logicIn logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
, S4Normal modal logicIn logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
, S5S5 (modal logic)In logic and philosophy, S5 is one of five systems of modal logic proposed byClarence Irving Lewis and Cooper Harold Langford in their 1932 book Symbolic Logic.It is a normal modal logic, and one of the oldest systems of modal logic of any kind....
, and wK4 are models of modal algebraModal logicModal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
, interior algebraInterior algebraIn abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic...
, monadic Boolean algebraMonadic Boolean algebraIn abstract algebra, a monadic Boolean algebra is an algebraic structure with signaturewhere ⟨A, ·, +, ', 0, 1⟩ is a Boolean algebra.The prefixed unary operator ∃ denotes the existential quantifier, which satisfies the identities:...
, and derivative algebraDerivative algebra (abstract algebra)In abstract algebra, a derivative algebra is an algebraic structure of the signature where is a Boolean algebra and D is a unary operator, the derivative operator, satisfying the identities: # 0D = 0 # xDD ≤ x + xD...
, respectively. - Any first-order theory whose sentencesSentence (mathematical logic)In mathematical logic, a sentence of a predicate logic is a boolean-valued well formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that may be true or false...
can be written in such a way that the quantifiers do not nest more than three deep, can be recast as a model of relation algebraRelation algebraIn mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
. Such models include Peano arithmetic and most axiomatic set theories, including ZFC, NBGVon Neumann–Bernays–Gödel set theoryIn the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
, and New FoundationsNew FoundationsIn mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
.
Ring-like structures
- N is a commutative semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
under addition and multiplication. - The set R[X] of all polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s over some coefficient ring R is a ring. - 2x2 matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
under matrix addition and multiplication form a ring. - If n is a positive integer, then the set Zn = Z/nZ of integers modulo n (the additive cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order n ) forms a ring having n elements (see modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
).
Field-like structures
- Z is an integral domain under addition and multiplication.
- Each of Q, R, C, and the p-adic integersP-adic numberIn mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
is a field under addition and multiplication. - Q and R are ordered fieldOrdered fieldIn mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
s, totally ordered by '≤'. - R is the:
- Only Dedekind complete ordered fieldOrdered fieldIn mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
, as the axioms for such a field are categoricalCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
; - Real fieldFormally real fieldIn mathematics, in particular in field theory and real algebra, a formally real field is a field that admits an ordering which makes it an ordered field.-Alternative Definitions:...
grounding realReal analysisReal analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
and functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
; - Filed whose subfields include the algebraicAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
, the computableComputable numberIn mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
, and the definable numberDefinable numberA real number a is first-order definable in the language of set theory, without parameters, if there is a formula φ in the language of set theory, with one free variable, such that a is the unique real number such that φ holds in the standard model of set theory .For the purposes of this article,...
s.
- Only Dedekind complete ordered field
- C is an algebraically closed fieldAlgebraically closed fieldIn mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
. - Some facts about finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s:- There exists a complete classification thereof.
- An algebraic number fieldAlgebraic number fieldIn mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
in number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
is a finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
extension of Q, that is, a field containing Q which has finite dimension as a vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over Q. - If q > 1 is a power of a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, then there exists (up toUp toIn mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
) exactly one finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with q elements, usually denoted Fq, or in the case that q is itself prime, by Z/qZ. Such fields are called Galois fields, whence the alternative notation GF(q). All finite fields are isomorphic to some Galois field. - Given some prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p, the set Zp = Z/pZ of integers modulo p is the finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with p elements: Fp = {0, 1, ..., p − 1} where the operations are defined by performing the operation in Z, dividing by p and taking the remainder; see modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
.
Lie groups: See table of Lie groups
Table of Lie groups
This article gives a table of some common Lie groups and their associated Lie algebras.The following are noted: the topological properties of the group , as well as on their algebraic properties .For more examples of Lie groups and other...
and list of simple Lie groups.
External links
- Jipsen:
- Alphabetical list of algebra structures; includes many not mentioned here.
- Online books and lecture notes.
- Map containing about 50 structures, some of which do not appear above. Likewise, most of the structures above are absent from this map.
- PlanetMath topic index.
- Hazewinkel, Michiel (2001) Encyclopaedia of Mathematics. Springer-Verlag.
- Mathworld page on abstract algebra.
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: Algebra by Vaughan Pratt.