List of circle topics - AbsoluteAstronomy.com

This list of circle topics includes things related to the geometric shape, either abstractly, as in idealizations studied by geometers, or concretely in physical space. It does not include metaphors like "inner circle" or "circular reasoning" in which the word does not refer literally to the geometric shape.

Geometry and other areas of mathematics

Annulus (mathematics)
Annulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
Apollonian circles
Apollonian circles
Apollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates...
Apollonian gasket
Apollonian gasket
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated from triples of circles, where each circle is tangent to the other two. It is named after Greek mathematician Apollonius of Perga.-Construction:...
Arbelos
Arbelos
In geometry, an arbelos is a plane region bounded by a semicircle of diameter 1, connected to semicircles of diameters r and , all oriented the same way and sharing a common baseline. Archimedes is believed to be the first mathematician to study its mathematical properties, as it appears in...
Archimedean circle
Archimedes' circles
Archimedes' circles
In geometry, Archimedes' circles, first created by Archimedes, are two circles that can be created inside of an arbelos, both having the same area as each other.-Construction:...
Archimedes' quadruplets
Archimedes' quadruplets
In geometry, Archimedes' quadruplets are four congruent circles associated with an arbelos. Introduced by Frank Power in the summer of 1998, each have the same area as Archimedes' twin circles, making them Archimedean circles.-Construction:...
Area of a disk
Bankoff circle
Bankoff circle
In geometry, the Bankoff circle or Bankoff triplet circle is a certain Archimedean circle that can be constructed from an arbelos; an Archimedean circle is any circle with area equal to each of Archimedes' twin circles. The Bankoff circle was first constructed by Leon Bankoff.-Construction:The...
Thomas Baxter (mathematician)
Thomas Baxter (mathematician)
Thomas Baxter , was a pseudo-mathematician.Baxter was the author of The Circle squared, . Starting from the assumption that ‘if the diameter of a circle be unity or one, the circumference of that circle will be 3.0625,’ the writer deduces some fourteen problems relative to circles. With more...
Belt problem
Belt problem
The belt problem is a mathematics problem which requires finding the length of a crossed belt that connects two circular pulleys with radius r1 and r2 whose centers are separated by a distance P...
Bertrand's paradox (probability)
Bertrand's paradox (probability)
The Bertrand paradox is a problem within the classical interpretation of probability theory. Joseph Bertrand introduced it in his work Calcul des probabilités as an example to show that probabilities may not be well defined if the mechanism or method that produces the random variable is not...
Bicentric quadrilateral
Bicentric quadrilateral
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. This means they have all the properties of both tangential quadrilaterals and cyclic quadrilaterals...
Bipolar coordinates
Bipolar coordinates
Bipolar coordinates are a two-dimensional orthogonal coordinate system. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates. There is also a third coordinate system that is based on two poles . The first is based on the Apollonian circles...
Bonnesen's inequality
Bonnesen's inequality
Bonnesen's inequality is an inequality relating the length, the area, the radius of the incircle and the radius of the circumcircle of a Jordan curve. It is a strengthening of the classical isoperimetric inequality....
Borromean rings
Borromean rings
In mathematics, the Borromean rings consist of three topological circles which are linked and form a Brunnian link, i.e., removing any ring results in two unlinked rings.- Mathematical properties :...
Brahmagupta's formula
Brahmagupta's formula
In Euclidean geometry, Brahmagupta's formula finds the area of any quadrilateral given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle.- Basic form :...
Brocard circle
Brocard circle
In geometry, the Brocard circle for a triangle is a circle having a diameter of the line segment between the circumcenter and symmedian. It contains the Brocard points. The Brocard circle is named for Henri Brocard....
Buffon's needle
Buffon's needle
In mathematics, Buffon's needle problem is a question first posed in the 18th century by Georges-Louis Leclerc, Comte de Buffon:Buffon's needle was the earliest problem in geometric probability to be solved; it can be solved using integral geometry...
Butterfly theorem
Butterfly theorem
The butterfly theorem is a classical result in Euclidean geometry, which can be stated as follows:Let M be the midpoint of a chord PQ of a circle, through which two other chords AB and CD are drawn; AD and BC intersect chord PQ at X and Y correspondingly...
Carnot's theorem
Carnot's theorem
In Euclidean geometry, Carnot's theorem, named after Lazare Carnot , is as follows. Let ABC be an arbitrary triangle. Then the sum of the signed distances from the circumcenter D to the sides of triangle ABC is...
Casey's theorem
Casey's theorem
In mathematics, Casey's theorem, also known as the generalized Ptolemy's theorem, is a theorem in Euclidean geometry named after the Irish mathematician John Casey.- Formulation of the theorem:...
Centered trochoid
Centered trochoid
In geometry, a centered trochoid is the roulette formed by a circle rolling along another circle. That is, the path traced by a point attached to a circle as the circle rolls without slipping along a fixed circle. The term encompasses both epitrochoid and hypotrochoid...
Circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
Central angle
Central angle
A central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...
Circle bundle
Circle graph
Circle graph
In graph theory, a circle graph is the intersection graph of a set of chords of a circle. That is, it is an undirected graph whose vertices can be associated with chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.-Algorithmic...
Circle group
- Group of rational points on the unit circle
  Group of rational points on the unit circle
  The rational points on the unit circle are those points such that both x and y are rational numbers and satisfy x2 + y2 = 1. The set of such points turns out to be closely related to primitive Pythagorean triples...
Circle map
Circle map
In mathematics, a circle map is a member of a family of dynamical systems on the circle first defined by Andrey Kolmogorov. Kolmogorov proposed this family as a simplified model for driven mechanical rotors . The circle map equations also describe a simplified model of the phase-locked loop in...
Circle packing
Circle packing
In geometry, circle packing is the study of the arrangement of circles on a given surface such that no overlapping occurs and so that all circles touch another. The associated "packing density", η of an arrangement is the proportion of the surface covered by the circles...
Circle packing in a circle
Circle packing in a circle
Circle packing in a circle is a two-dimensional packing problem with the objective of packing unit circles into the smallest possible larger circle.Minimum solutions:...
Circle packing in an equilateral triangle
Circle packing in an equilateral triangle
Circle packing in an equilateral triangle is a packing problem in discrete mathematics where the objective is to pack n unit circles into the smallest possible equilateral triangle...
Circle packing in an isosceles right triangle
Circle packing in an isosceles right triangle
Circle packing in a right isosceles triangle is a packing problem where the objective is to pack n unit circles into the smallest possible isosceles right triangle.Minimum solutions are shown in the table below...
Circle packing theorem
Circle packing theorem
The circle packing theorem describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles whose interiors are disjoint...
Circles of Apollonius
Circles of Apollonius
The term circle of Apollonius is used to describe several types of circles associated with Apollonius of Perga, a renowned Greek geometer. Most of these circles are found in planar Euclidean geometry, but analogs have been defined on other surfaces; for example, counterparts on the surface of a...
Circle of antisimilitude
Circle of antisimilitude
In geometry, the circle of antisimilitude of two circles α and β is a circle for which α and β are inverses of each other. If α and β are non-intersecting or tangent, there exists one circle of antisimilitude; if α and β intersect at two points, there exist two circles of antisimilitude...
Circular algebraic curve
Circular algebraic curve
In geometry, a circular algebraic curve is a type of plane algebraic curve determined by an equation F = 0, where F is a polynomial with real coefficients and the highest-order terms of F form a polynomial divisible by x2 + y2...
Circular distribution
Circular sector
Circular sector
A circular sector or circle sector, is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, r the radius of the circle, and L is the arc length of the...
Circular segment
Circular segment
In geometry, a circular segment is an area of a circle informally defined as an area which is "cut off" from the rest of the circle by a secant or a chord. The circle segment constitutes the part between the secant and an arc, excluding the circle's center...
Circular statistics
Circular statistics
Directional statistics is the subdiscipline of statistics that deals with directions , axes or rotations in Rn...
Circular surface
Circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
Circumscribed circle
Circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....

— Circumcircle
Clifford's circle theorems
Clifford's circle theorems
In geometry, Clifford's theorems, named after the English geometer William Kingdon Clifford, are a sequence of theorems relating to intersections of circles.The first theorem considers any four circles passing through a common point M...
Coaxal circles
Compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
- Mohr–Mascheroni theorem
  Mohr–Mascheroni theorem
  In mathematics, the Mohr–Mascheroni theorem states that any geometric construction that can be performed by a compass and straightedge can be performed by a compass alone. The result was originally published by Georg Mohr in 1672, but his proof languished in obscurity until 1928. The theorem was...
- Poncelet–Steiner theorem
Concentric
Concentric
Concentric objects share the same center, axis or origin with one inside the other. Circles, tubes, cylindrical shafts, disks, and spheres may be concentric to one another...
Concyclic
Coxeter's loxodromic sequence of tangent circles
Coxeter's loxodromic sequence of tangent circles
In geometry, Coxeter's loxodromic sequence of tangent circles is an infinite sequence of circles arranged such that any four consecutive circles in the sequence are pairwise mutually tangent...
Cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
Cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
Descartes' theorem
Descartes' theorem
In geometry, Descartes' theorem, named after René Descartes, establishes a relationship between four kissing, or mutually tangent, circles. The theorem can be used to construct a fourth circle tangent to three given, mutually tangent circles.-History:...
Diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
Dinostratus' theorem
Dinostratus' theorem
[File:Quadratrix des Dinostratos.svg|thumb|\frac[File:Quadratrix des Dinostratos.svg|thumb|\frac[File:Quadratrix des Dinostratos.svg|thumb|\frac[[File:Quadratrix des Dinostratos.svg|thumb|\frac[[File:Quadratrix des Dinostratos.svg|thumb|\frac...
Director circle
Director circle
In geometry, the director circle of an ellipse or hyperbola is a circle formed by the points where two perpendicular tangent lines to the curve cross....
Disk (mathematics)
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
Dividing a circle into areas
Dividing a circle into areas
In geometry, the problem of dividing a circle into areas by means of an inscribed polygon with n sides, in such a way as to maximise the number of areas created by the edges and diagonals, has a solution by an inductive method.- Lemma :...
Epitrochoid
Epitrochoid
An epitrochoid is a roulette traced by a point attached to a circle of radius r rolling around the outside of a fixed circle of radius R, where the point is a distance d from the center of the exterior circle....
- Epicycloid
  Epicycloid
  In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle...
  - Cardioid
    Cardioid
    A cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It is therefore a type of limaçon and can also be defined as an epicycloid having a single cusp...
  - Nephroid
    Nephroid
    The nephroid is a plane curve whose name means kidney-shaped Although the term nephroid was used to describe other curves, it was applied to the curve in this article by Proctor in 1878. This and the information below may be verified in Lockwood, pp...
  - Deferent and epicycle
    Deferent and epicycle
    In the Ptolemaic system of astronomy, the epicycle was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets...
Equal incircles theorem
Equal incircles theorem
In geometry, the equal incircles theorem derives from a Japanese Sangaku, and pertains to the following construction: a series of rays are drawn from a given point to a given line such that the inscribed circles of the triangles formed by adjacent rays and the base line are equal...
Ex-tangential quadrilateral
Ex-tangential quadrilateral
In Euclidean geometry, an ex-tangential quadrilateral is a convex quadrilateral where the extensions of all four sides are tangent to a circle outside the quadrilateral. It has also been called an exscriptible quadrilateral. The circle is called its excircle or its escribed circle, its radius the...
Fermat–Apollonius circle
Five circles theorem
Five circles theorem
In geometry, the five circles theorem states that, given five circles centered on a common sixth circle and intersecting each other chainwise on the same circle, the lines joining the their second intersection points forms a pentagram whose points lie on the circles themselves....
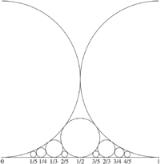
Ford circle
Ford circle
In mathematics, a Ford circle is a circle with centre at and radius 1/, where p/q is an irreducible fraction, i.e. p and q are coprime integers...
Fuhrmann circle
Fuhrmann circle
In geometry, the Fuhrmann circle of a triangle is the circle with a diameter of the line segment between the orthocenter and the Nagel point. The radius of the Fuhrmann circle of a triangle with sides a, b, and c and circumradius R is...
Gauss circle problem
Gauss circle problem
In mathematics, the Gauss circle problem is the problem of determining how many integer lattice points there are in a circle centred at the origin and with radius r. The first progress on a solution was made by Carl Friedrich Gauss, hence its name....
Geometrography
Geometrography
In mathematics, in geometry, geometrography is the study of geometrical constructions. The concepts and methods of geometrography were first expounded by Émile Lemoine , a French civil engineer and a mathematician, in a meeting of the French Association for the Advancement of the Sciences held at...
Generalised circle
Generalised circle
A generalized circle, also referred to as a "cline" or "circline", is a straight line or a circle. The concept is mainly used in inversive geometry, because straight lines and circles have very similar properties in that geometry and are best treated together....
Gershgorin circle theorem
Gershgorin circle theorem
In mathematics, the Gershgorin circle theorem may be used to bound the spectrum of a square matrix. It was first published by the Belarusian mathematician Semyon Aranovich Gershgorin in 1931. The spelling of S. A...
GEOS circle
GEOS circle
In geometry, the GEOS circle is derived from the intersection of four lines that are associated with a generalized triangle: the Euler line, the Soddy line, the orthic axis and the Gergonne line...
Great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
- Great-circle distance
  Great-circle distance
  The great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
- Circle of a sphere
Hadamard three-circle theorem
Hadamard three-circle theorem
In complex analysis, a branch of mathematics, theHadamard three-circle theorem is a result about the behavior of holomorphic functions.Let f be a holomorphic function on the annulusr_1\leq\left| z\right| \leq r_3....
Hardy–Littlewood circle method
Hawaiian earring
Hawaiian earring
In mathematics, the Hawaiian earring H is the topological space defined by the union of circles in the Euclidean plane R2 with center and radius 1/n for n = 1, 2, 3, ......
Homothetic center
Homothetic center
In geometry, a homothetic center is a point from which at least two geometrically similar figures can be seen as a dilation/contraction of one another. If the center is external, the two figures are directly similar to one another; their angles have the same rotational sense...
Horn angle
Horn angle
A horn angle, also called a cornicular angle, is a type of curvilinear angle defined as the angle formed between a circle and a straight line tangent to it, or, more generally, the angle formed between two curves at a point where they are tangent to each other...
Horocycle
Horocycle
In hyperbolic geometry, a horocycle is a curve whose normals all converge asymptotically. It is the two-dimensional example of a horosphere ....
Hypotrochoid
Hypotrochoid
A hypotrochoid is a roulette traced by a point attached to a circle of radius r rolling around the inside of a fixed circle of radius R, where the point is a distance d from the center of the interior circle....
- Hypocycloid
  Hypocycloid
  In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle...
  - Astroid
  - Deltoid curve
    Deltoid curve
    In geometry, a deltoid, also known as a tricuspoid or Steiner curve, is a hypocycloid of three cusps. In other words, it is the roulette created by a point on the circumference of a circle as it rolls without slipping along the inside of a circle with three times its radius...
Incircle and excircles of a triangle
Incircle and excircles of a triangle
In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides...
Inscribed angle
Inscribed angle
In geometry, an inscribed angle is formed when two secant lines of a circle intersect on the circle....
Inscribed angle theorem
Inscribed circle
Inversive distance
Inversive distance
Inversive distance is a way of measuring the "distance" between two non-intersecting circles α and β. If α and β are inverted with respect to a circle centered at one of the limiting points of the pencil of α and β, then α and β will invert into concentric circles...
Inversive geometry
Irrational rotation
Irrational rotation
In mathematical theory of dynamical systems, an irrational rotation is a mapwhere θ is an irrational number. Under the identification of a circle with R/Z, or with the interval [0, 1] with the boundary points glued together, this map becomes a rotation of a circle by a proportion θ of a full...
Isodynamic point
Isodynamic point
In Euclidean geometry, every triangle has two isodynamic points, usually denoted as S and S^'. These points are the common intersection points of the three circles of Apollonius associated with the triangle; hence, the line through these points is the common radical axis for these circles...
Isoperimetric problem
Isoperimetric problem
Isoperimetric problem may refer to:* Isoperimetric inequality* Any problem in calculus of variations...
Japanese theorem for concyclic polygons
Japanese theorem for concyclic quadrilaterals
Japanese theorem for concyclic quadrilaterals
In geometry, the Japanese theorem states that the centers of the incircles of certain triangles inside a cyclic quadrilateral are vertices of a rectangle....
Johnson circles
Johnson circles
In geometry, a set of Johnson circles comprise three circles of equal radius r sharing one common point of intersection H. In such a configuration the circles usually have a total of four intersections : the common point H that they all share, and for each of the three pairs of circles one more...
Lemoine line
Lester's theorem
Lester's theorem
In Euclidean plane geometry, Lester's theorem, named after June Lester, states that in any scalene triangle, the two Fermat points, the nine-point center, and the circumcenter are concyclic.- References :...
Limiting cases of Apollonius' problem
Limiting cases of Apollonius' problem
In Euclidean geometry, Apollonius' problem is to construct all the circles that are tangent to three given circles. Limiting cases of Apollonius' problem are those in which at least one of the given circles is a point or line, i.e., is a circle of zero or infinite radius...
List of topics related to pi
Lune
Lune (mathematics)
In geometry, a lune is either of two figures, both shaped roughly like a crescent Moon. The word "lune" derives from luna, the Latin word for Moon.-Plane geometry:...
Lune of Hippocrates
Lune of Hippocrates
In geometry, the lune of Hippocrates, named after Hippocrates of Chios, is a lune bounded by arcs of circles, one of which passes through the center of the other and has half the area of the other...
Magic circle (mathematics)
Magic circle (mathematics)
Magic circles were invented by the Song Dynasty Chinese mathematician Yang Hui . It is the arrangement of natural numbers on circles where the sum of the numbers on each circle and the sum of numbers on diameter are identical...
Malfatti circles
Malfatti circles
In geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the triangle...
Measurement of a Circle
Measurement of a Circle
Measurement of a Circle is a treatise that consists of three propositions by Archimedes. The treatise is only a fraction of what was a longer work.-Proposition one:Proposition one states:...
Midpoint-stretching polygon
Midpoint-stretching polygon
In geometry, the midpoint-stretching polygon of a cyclic polygon is the polygon whose vertices are the midpoints of the circular arcs between the vertices of . It is also called the shadow of ....
Milne-Thomson circle theorem
Miquel's theorem
Miquel's theorem
Miquel's theorem is a theorem in geometry, named after Auguste Miquel, about the intersection pattern of circles defined from six points on a triangle...
Monge's theorem
Monge's theorem
In geometry, Monge's theorem, named after Gaspard Monge, states that for any three circles in a plane, none of which is inside one of the others, the three intersection points of the three pairs of external tangent lines are in fact collinear....
Mean of circular quantities
Mean of circular quantities
In mathematics, a mean of circular quantities is a mean which is suited for quantities like angles, daytimes, and fractional parts of real numbers. This is necessary since most of the usual means fail on circular quantities...
Mrs. Miniver's problem
Mrs. Miniver's problem
Mrs. Miniver's problem is a geometry problem about circles. Given a circle A, find a circle B such that the area of the intersection of A and B is equal to the area of the symmetric difference of A and B .The problem derives from "A Country House Visit", one of Jan Struther's newspaper articles...
Nine-point circle
Nine-point circle
In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant points defined from the triangle...
Osculating circle
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
Ortsbogen theorem
Ortsbogen theorem
In geometry, for any line segment AB and angle θ < π, the locus of points C on one side of line AB such that angle ACB equals θ is an arc of a circle...
Pappus chain
Pappus chain
In geometry, the Pappus chain was created by Pappus of Alexandria in the 3rd century AD.-Construction:The arbelos is defined by two circles, CU and CV, which are tangent at the point A and where CU is enclosed by CV...
Peaucellier–Lipkin linkage
Pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
Pivot theorem
Pivot theorem
In geometry, the pivot theorem states that, given any three points P, Q, and R on each respective side of a triangle ABC, the three circles through the points AQR, BPR and CPQ share a common point M...
Pizza theorem
Pizza theorem
In elementary geometry, the pizza theorem states the equality of two areas that arise when one partitions a disk in a certain way.Let p be an interior point of the disk, and let n be a number that is evenly divisible by four and greater than or equal to eight...
Pole and polar
Pole and polar
In geometry, the terms pole and polar are used to describe a point and a line that have a unique reciprocal relationship with respect to a given conic section...
Polygon-circle graph
Polygon-circle graph
In the mathematical discipline of graph theory, a polygon-circle graph, also called a spider graph, is a type of an intersection graph, where each vertex is represented as a polygon and each edge as an intersection of two polygons representing those vertices, enclosed by a bounding circle. All...

Polygon-circle graph
In the mathematical discipline of graph theory, a polygon-circle graph, also called a spider graph, is a type of an intersection graph, where each vertex is represented as a polygon and each edge as an intersection of two polygons representing those vertices, enclosed by a bounding circle. All...
Poncelet's porism
Poncelet's porism
In geometry, Poncelet's porism, named after French engineer and mathematician Jean-Victor Poncelet, states the following: Let C and D be two plane conics...
Power center (geometry)
Power of a point
Power of a point
In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle C of radius r is defined...
Problem of Apollonius
Problem of Apollonius
In Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane . Apollonius of Perga posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria has survived...
Proof that pi is irrational
Ptolemy's theorem
Ptolemy's theorem
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral . The theorem is named after the Greek astronomer and mathematician Ptolemy...
Ptolemy's table of chords
Ptolemy's table of chords
The table of chords, created by the astronomer and geometer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function...
Radical axis
Radical axis
The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...
Radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
- Radius of convergence
  Radius of convergence
  In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
- Radius of curvature
  Radius of curvature
  The distance from the center of a circle or sphere to its surface is its radius. For other curved lines or surfaces, the radius of curvature at a given point is the radius of a circle that mathematically best fits the curve at that point....
Regiomontanus' angle maximization problem
Regiomontanus' angle maximization problem
In mathematics, the Regiomontanus' angle maximization problem, is a famous optimization problem posed by the 15th-century German mathematician Johannes Müller...
Riemannian circle
Riemannian circle
In metric space theory and Riemannian geometry, the Riemannian circle is a great circle equipped with its great-circle distance...
Robbins pentagon
Robbins pentagon
A Robbins pentagon, named after David P. Robbins, is a cyclic polygon with five integer sides and integer area. It also has the property that all its diagonals are rational, meaning that it can be decomposed into Heron triangles. The converse is not necessarily true. Three Heron triangles cannot...
Salinon
Salinon
The salinon is a geometrical figure that consists of four semicircles. It was first introduced by Archimedes in his Book of Lemmas.-Construction:...
Schoch line
Schoch line
In geometry, the Schoch line was created by Thomas Schoch. The line originated from Schoch's dozen circles.- Construction :With an arbelos two circular arcs K1 and K2 are created with the centers at point A and C, respectively. A circle, with the center A1, is then created tangent to the arcs...
Schoch circles
Schoch circles
In geometry, the Schoch circles are twelve Archimedean circles constructed by Thomas Schoch.-History:In 1979, Thomas Schoch discovered a dozen new Archimedean circles; he sent his discoveries to Scientific American's "Mathematical Games" editor Martin Gardner. The manuscript was forwarded to Leon...
Semicircle
Semicircle
In mathematics , a semicircle is a two-dimensional geometric shape that forms half of a circle. Being half of a circle's 360°, the arc of a semicircle always measures 180° or a half turn...
Seven circles theorem
Seven circles theorem
In geometry, the seven circles theorem is a theorem about a certain arrangement of seven circles in the Euclidean plane. Specifically, given a chain of six circles all tangent to a seventh circle and each tangent to its two neighbors, the three lines drawn between the six points of tangency with...
Six circles theorem
Six circles theorem
In geometry, the six circles theorem relates to a chain of six circles together with a triangle, such that each circle is tangent to two sides of the triangle and also to the preceding circle in the chain...
Smallest circle problem
Smallest circle problem
The smallest circle problem or minimum covering circle problem is a mathematical problem of computing the smallest circle that contains all of a given set of points in the Euclidean plane. The corresponding problem in n-dimensional space, the smallest bounding sphere problem, is to compute the...
Spieker circle
Spieker circle
In geometry, the incircle of the medial triangle of a triangle ABC is the Spieker circle. Its center, the Spieker center, is the center of mass of the boundary of triangle ABC as well as being the incenter of the medial triangle....
Splitting circle
Squaring the circle
Squaring the circle
Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
Squircle
Squircle
A squircle is a mathematical shape with properties between those of a square and those of a circle. It is a special case of superellipse. The word "squircle" is a portmanteau of the words, "square" and "circle".-Equation:...
Steiner chain
Steiner chain
In geometry, a Steiner chain is a set of n circles, all of which are tangent to two given non-intersecting circles , where n is finite and each circle in the chain is tangent to the previous and next circles in the chain...
Tammes problem
Tammes problem
In geometry, Tammes problem is a problem in packing a given number of circles on the surface of a sphere such that the minimum distance between circles is maximized. It is named after a Dutch botanist who posed the problem in 1930 while studying the distribution of pores on pollen grains...
Tangent lines to circles
Tangent lines to circles
In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...
Tangent circles
Tangent circles
In geometry, tangent circles are circles in a common plane that intersect in a single point. There are two types of tangency: internal and external...
Tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
Tarski's circle-squaring problem
Tarski's circle-squaring problem
Tarski's circle-squaring problem is the challenge, posed by Alfred Tarski in 1925, to take a disc in the plane, cut it into finitely many pieces, and reassemble the pieces so as to get a square of equal area. This was proven to be possible by Miklós Laczkovich in 1990; the decomposition makes heavy...
Thales' theorem
Thales' theorem
In geometry, Thales' theorem states that if A, B and C are points on a circle where the line AC is a diameter of the circle, then the angle ABC is a right angle. Thales' theorem is a special case of the inscribed angle theorem...
Unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
Versor
Villarceau circles
Villarceau circles
In geometry, Villarceau circles are a pair of circles produced by cutting a torus diagonally through the center at the correct angle. Given an arbitrary point on a torus, four circles can be drawn through it. One is in the plane parallel to the equatorial plane of the torus. Another is...
von Mises distribution
Wigner semicircle distribution
Woo circles
Woo circles
In geometry, the Woo circles, introduced by Peter Y. Woo, are a set of infinitely many Archimedean circles.-Construction:Form an arbelos with the two inner semicircles tangent at point C. Let m denote any nonnegative real number. Draw two circles, with radii m times the radius of the smaller two...
Wrapped distribution
Wrapped distribution
In probability theory and directional statistics, a wrapped probability distribution is a continuous probability distribution that describes data points that lie on a unit n-sphere...
- Wrapped Cauchy distribution
- Wrapped normal distribution
  Wrapped normal distribution
  In probability theory and directional statistics, a wrapped normal distribution is a wrapped probability distribution which results from the "wrapping" of the normal distribution around the unit circle. It finds application in the theory of Brownian motion and is a solution to the heat equation for...

Physics

Centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
Centripetal force
Centripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
Circle of confusion
Circle of confusion
In optics, a circle of confusion is an optical spot caused by a cone of light rays from a lens not coming to a perfect focus when imaging a point source...

Circle of confusion
In optics, a circle of confusion is an optical spot caused by a cone of light rays from a lens not coming to a perfect focus when imaging a point source...
Circular dichroism
Circular dichroism
Circular dichroism refers to the differential absorption of left and right circularly polarized light. This phenomenon was discovered by Jean-Baptiste Biot, Augustin Fresnel, and Aimé Cotton in the first half of the 19th century. It is exhibited in the absorption bands of optically active chiral...
Circular orbit
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
Mohr's circle
Non-uniform circular motion
Non-uniform circular motion
Non-uniform circular motion is any case in which an object moving in a circular path has a varying speed. Some examples of non-uniform circular motion include a roller coaster, a vertical pendulum, and a car riding over a hill. All of these situations include an object traveling at different...
Thomson problem
Thomson problem
The Thomson problem is to determine the minimum energy configuration of N electrons on the surface of a sphere that repel each other with a force given by Coulomb's law. The physicist J. J...
Uniform circular motion
Uniform circular motion
In physics, uniform circular motion describes the motion of a body traversing a circular path at constant speed. The distance of the body from the axis of rotation remains constant at all times. Though the body's speed is constant, its velocity is not constant: velocity, a vector quantity, depends...

Geography

Arctic Circle
Arctic Circle
The Arctic Circle is one of the five major circles of latitude that mark maps of the Earth. For Epoch 2011, it is the parallel of latitude that runs north of the Equator....
Antarctic Circle
Antarctic Circle
The Antarctic Circle is one of the five major circles of latitude that mark maps of the Earth. For 2011, it is the parallel of latitude that runs south of the Equator.-Description:...
Circle of latitude
Circle of latitude
A circle of latitude, on the Earth, is an imaginary east-west circle connecting all locations that share a given latitude...
Equator
Equator
An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
Great-circle distance
Great-circle distance
The great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
Position circle
Position circle
A position circle is a circle that can be measured both from a chart and from the surface of the earth for the purpose of position fixing. The circles can be measured by sextant. Two overlapping position circles can be used to give a position fix.-See also:...

Artifacts

Addendum circle
Belt problem
Belt problem
The belt problem is a mathematics problem which requires finding the length of a crossed belt that connects two circular pulleys with radius r1 and r2 whose centers are separated by a distance P...
Circular ditches
Circular ditches
About 150 arrangements of prehistoric circular ditches are known to archaeologists spread over Germany, Austria, Slovakia, and the Czech Republic. Their diameters range from ca. 20 to ca. 130 m, and they date to the 5th millennium BC. Tools, bones, and some artefacts were found in their context....
Circular slide rule
Compass (drafting)
Compass (drafting)
A compass or pair of compasses is a technical drawing instrument that can be used for inscribing circles or arcs. As dividers, they can also be used as a tool to measure distances, in particular on maps...
Crop circle
Crop circle
A crop circle is a sizable pattern created by the flattening of a crop such as wheat, barley, rye, maize, or rapeseed. Crop circles are also referred to as crop formations, because they are not always circular in shape. While the exact date crop circles began to appear is unknown, the documented...
Dip circle
Dip circle
Dip circles are used to measure the angle between the horizon and the Earth's magnetic field . They were used in surveying, mining and prospecting as well as for the demonstration and study of magnetism....
List of gear nomenclature
Peaucellier–Lipkin linkage
Pitch circle
Repeating circle
Repeating circle
The repeating circle is an instrument for geodetic surveying, invented by Etienne Lenoir in 1784, while an assistant of Jean-Charles de Borda, who later improved the instrument. It was notable as being the equal of the great theodolite created by the renowned instrument maker, Jesse Ramsden...
Timber circle
Timber circle
In archaeology, timber circles are circular arrangements of wooden posts interpreted as being either complexes of freestanding totem poles or as the supports for large circular buildings-British Isles:...
Traffic circle
Traffic circle
A traffic circle or rotary is a type of circular intersection in which traffic must travel in one direction around a central island. In some countries, traffic entering the circle has the right-of-way and drivers in the circle must yield. In many other countries, traffic entering the circle must...
- List of circles in Washington, D.C.
- List of traffic circles in New Jersey
Setting circles
Setting circles
Setting circles are used on telescopes equipped with an equatorial mount to find astronomical objects in the sky by their equatorial coordinates often used in star charts or ephemeris.-Description:...
Stone circle
Stone circle
A stone circle is a monument of standing stones arranged in a circle. Such monuments have been constructed across the world throughout history for many different reasons....
Wheel
Wheel
A wheel is a device that allows heavy objects to be moved easily through rotating on an axle through its center, facilitating movement or transportation while supporting a load, or performing labor in machines. Common examples found in transport applications. A wheel, together with an axle,...

Glyphs and symbols

Borromean rings
Borromean rings
In mathematics, the Borromean rings consist of three topological circles which are linked and form a Brunnian link, i.e., removing any ring results in two unlinked rings.- Mathematical properties :...
Circled dot
Circled dot
The circled dot, circumpunct, or circle with a point at its centre is an ancient symbol. It can represent:Solar symbol*Solar symbol, symbol used to represent the sun* Solar mass * The sun / Gold...
Circles in Polish mythology
Crescent
Crescent
In art and symbolism, a crescent is generally the shape produced when a circular disk has a segment of another circle removed from its edge, so that what remains is a shape enclosed by two circular arcs of different diameters which intersect at two points .In astronomy, a crescent...
Enso
Enso
Ensō is a Japanese word meaning "circle" and a concept strongly associated with Zen. Ensō is one of the most common subjects of Japanese calligraphy even though it is a symbol and not a character. It symbolizes the Absolute enlightenment, strength, elegance, the Universe, and the void; it can...
Flower of Life
Flower of Life
The Flower of Life is the modern name given to a geometrical figure composed of multiple evenly-spaced, overlapping circles. They are arranged to form a flower-like pattern with a sixfold symmetry, similar to a hexagon...
Olympic emblem
Olympic symbols
The Olympic symbols are icons, flags and symbols used by the International Olympic Committee to promote the Olympic Games. Some—such as the flame, fanfare, and theme—are more common during Olympic competition, but others, such as the flag, can be seen throughout the year.-Motto:The Olympic motto is...
Ouroboros
Ouroboros
The Ouroboros is an ancient symbol depicting a serpent or dragon eating its own tail. The name originates from within Greek language; οὐρά meaning "tail" and βόρος meaning "eating", thus "he who eats the tail"....
Petosiris to Nechepso
Petosiris to Nechepso
Petosiris to Nechepso is a letter describing an ancient divination technique using numerology and a diagram. It is likely to be a pseudepigraph. Petosiris and Nechepso are considered to be the founders of astrology in some traditions...
Quatrefoil
Quatrefoil
The word quatrefoil etymologically means "four leaves", and applies to general four-lobed shapes in various contexts.-In heraldry:In heraldic terminology, a quatrefoil is a representation of a flower with four petals, or a leaf with four leaflets . It is sometimes shown "slipped", i.e. with an...
Ring (diacritic)
Ring (diacritic)
A ring diacritic may appear above or below letters. It may be combined with some letters of the extended Latin alphabets in various contexts.-Ring above:...
Roundel
Roundel
A roundel in heraldry is a disc; the term is also commonly used to refer to a type of national insignia used on military aircraft, generally circular in shape and usually comprising concentric rings of different colours.-Heraldry:...
Sacred Chao
Shield of the Trinity
Shield of the Trinity
The Shield of the Trinity or Scutum Fidei is a traditional Christian visual symbol which expresses many aspects of the doctrine of the Trinity, summarizing the first part of the Athanasian Creed in a compact diagram...
Solar symbol
Solar symbol
A solar symbol is a symbol which symbolises the Sun. Solar symbols can have significance in psychoanalysis, symbolism, semiotics, astrology, religion, mythology, mysticism, divination, heraldry, and vexillology, among other fields.Some solar symbols include:...

s
Squared-circle postmark
Squared-circle postmark
A squared-circle postmark is a type of postmark that surrounds the circle of town and date with a set of concentric arcs forming a square outline....
Sun cross
Sun cross
The sun cross, also known as the wheel cross, Odin's cross, or Woden's cross, a cross inside a circle, is a common symbol in artifacts of the Americas and Prehistoric Europe, particularly during the Neolithic to Bronze Age periods.-Stone Age:...
Symbol of Tanit
Tanit
Tanit was a Phoenician lunar goddess, worshipped as the patron goddess at Carthage. Tanit was worshiped in Punic contexts in the Western Mediterranean, from Malta to Gades into Hellenistic times. From the fifth century BCE onwards Tanit is associated with that of Baal Hammon...
Trefoil
Trefoil
Trefoil is a graphic form composed of the outline of three overlapping rings used in architecture and Christian symbolism...
Triquetra
Triquetra
Triquetra originally meant "triangle" and was used to refer to various three-cornered shapes. Nowadays, it has come to refer exclusively to a particular more complicated shape formed of three vesicae piscis, sometimes with an added circle in or around it...
Vesica piscis
Vesica piscis
The vesica piscis is a shape that is the intersection of two circles with the same radius, intersecting in such a way that the center of each circle lies on the circumference of the other. The name literally means the "bladder of a fish" in Latin...
Triple Goddess symbol
Triple Goddess
The Triple Goddess is the subject of much of the writing of Robert Graves, and has been adopted by some neopagans as one of their primary deities. The term triple goddess is sometimes used outside of Neopaganism to refer to historical goddess triads and single goddesses of three forms or aspects...
Yin-yang
Yin and yang
In Asian philosophy, the concept of yin yang , which is often referred to in the West as "yin and yang", is used to describe how polar opposites or seemingly contrary forces are interconnected and interdependent in the natural world, and how they give rise to each other in turn. Opposites thus only...

Geometry and other areas of mathematics

Physics

Geography

Artifacts

Glyphs and symbols

See also